Bhushan B. Nanotribology and Nanomechanics: An Introduction

Подождите немного. Документ загружается.

1002 B. Bhushan et al.

Equation (19.5) provides with the value of the static contact angle for given surface

energies. Note that although we use the term “air”, the analysis does not change in

the case of another gas, such as water vapor.

19.2.2 Heterogeneous Interfaces and the Wenzel

and Cassie–Baxter Equations

In this section, we will discuss the so-called heterogeneous interface and intro-

duce the equations that govern the contact angle for the heterogeneous inter-

face.

Contact Angle with a Rough and HeterogeneousSurfaces

The Wenzel [133] equation, which was derived using the surface force balance and

empirical considerations, relates contact angle of a water droplet upon a rough

solid surface, θ, with that upon a smooth surface, θ

(Fig. 19.1b), through the non-

dimensionalsurface roughness factor, R

, equal to the ratio of the surface area to its

ﬂat projected area

cosθ =

= R

cosθ

(19.6)

. (19.7)

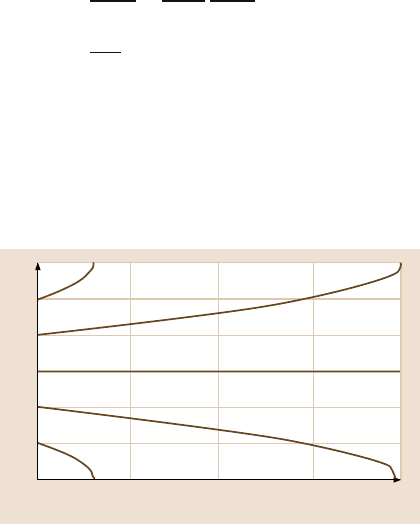
The dependence of the contact angle on the roughness factor is presented in

Fig. 19.2 for diﬀerent values of θ

. The Wenzel model predicts that a hydropho-

bic surface (θ

> 90

◦

) becomes more hydrophobic with an increase in R

, while

a hydrophilic surface (θ

< 90

◦

) becomes more hydrophilic with an increase in

[67,97].

1.25 1.50 1.75 2

180

= 120°

= 90°

= 60°

= 30°

150

120

= 150°

Fig. 19.2. Contact angle for

rough surface (θ) as a func-

tion of the roughness factor

) for various contact

angles for smooth surface

(θ

) [97]

19 Lotus Eﬀect: Roughness-Induced Superhydrophobic Surfaces 1003

In a similar manner, for a surface composed of two fractions, one with the frac-

tional area f

and the contact angle θ

and the other with f

and θ

respectively (so

that f

+ f

= 1), the contact angle is given by the Cassie equation

cosθ = f

cosθ

+ f

cosθ

. (19.8)

For the case of a composite interface (Fig. 19.1c), consisting of the solid-liquid

fraction (f

= f

, θ

= θ

) and liquid-air fraction (f

= f

= 1− f

,cosθ

= −1),

combining (19.7) and (19.8) yields the Cassie–Baxter equation

cosθ = R

cosθ

−1+ f

cosθ = R

cosθ

− f

cosθ

+ 1) . (19.9)

The opposite limiting case of cosθ

= 1(θ

= 0

◦

corresponds to the water-on-water

contact) yields

cosθ = 1+ f

(cosθ

−1) . (19.10)

Equation (19.10) is used sometimes [41] for the homogeneous interface instead

of (19.6), if the rough surface is covered by holes ﬁlled with water (Fig. 19.1d).

The Cassie–Baxter Equation

Two situations in wetting of a rough surface should be distinguished: the homo-

geneous interface without any air pockets (sometimes called the Wenzel interface,

since the contact angle is given by the Wenzel equation or (19.6)) and the composite

interface with air pockets trapped between the rough details as shown in Fig. 19.3a

(sometimes called the Cassie or Cassie–Baxter interface, since the contact angle is

given by (19.9)).

While (19.9) for the composite interface was derived using (19.6) and (19.8), it

could also be obtained independently. For this purpose, two sets of interfaces are

considered: a liquid-air interface with the ambient and a ﬂat composite interface un-

der the droplet, which itself involves solid-liquid,liquid-air,and solid-air interfaces.

For fractional ﬂat geometrical areas of the solid-liquid and liquid-air interfaces un-

der the droplet, f

and f

, the ﬂat area of the composite interface is

= f

+ f

= R

+ f

. (19.11)

In order to calculate the contact angle in a manner similar to the derivationof (19.6),

the diﬀerential area of the liquid-air interface under the droplet, f

, should be

subtracted from the diﬀerential of the total liquid-air area dA

, which yields

cosθ =

− f

= R

cosθ

− f

= R

cosθ

− f

cos

+1). (19.12)

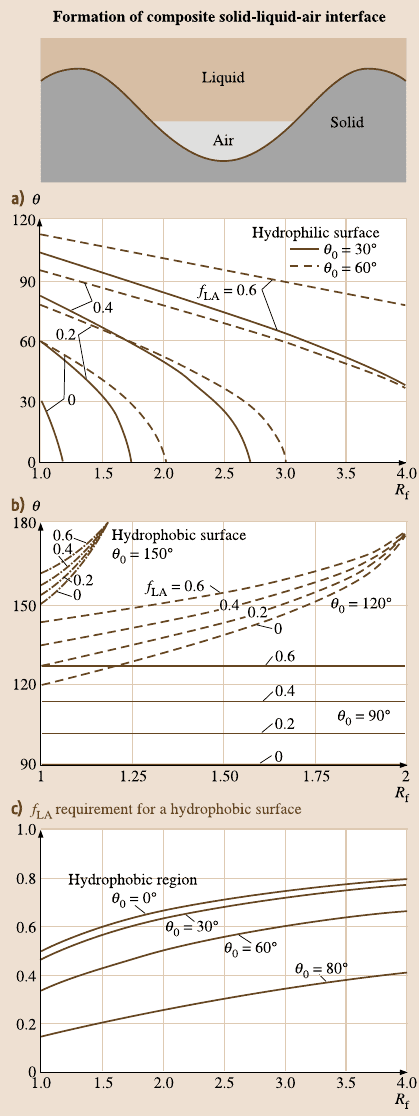
1004 B. Bhushan et al.

Fig. 19.3. (a) Formation of

a composite solid-liquid-air

interface for rough surface,

(b) contact angle for rough

surface (θ) as a function of

the roughness factor (R

)

for various f

values on

the hydrophilic surface and

the hydrophobic surface,

and (c) f

requirement for

a hydrophilic surface to be

hydrophobic as a function of

the roughness factor (R

)and

[67]

19 Lotus Eﬀect: Roughness-Induced Superhydrophobic Surfaces 1005

The dependence of the contact angle on the roughness factor for hydrophilic and

hydrophobic surfaces is presented in Fig. 19.3b.

According to (19.12), even for a hydrophilic surface, the contact angle increases

with an increase of f

. At a high value of f

, surface can become hydrophobic;

however, the value required may be unachievable or formation of air pockets may

become unstable. Using the Cassie–Baxter equation, the valueof f

at which a hy-

drophilic surface could turn into a hydrophobicone, is given by [67]

≥

cosθ

+ 1

for θ

< 90

◦

. (19.13)

Figure19.3c shows thevalueof f

requirementas a functionof R

for foursurfaces

with diﬀerent contact angles, θ

. Hydrophobic surfaces can be achieved abovea cer-

tain f

values as predicted by (19.13). The upper part of each contact angle line

is hydrophobicregion. For the hydrophobicsurface, contact angle increases with an

increase in f

both for smooth and rough surfaces.

Shuttleworth and Bailey [124] studied spreading of a liquid over a rough solid

surface and found that the contact angle at the absolute minimum of surface en-

ergy corresponds to the values, given by (19.6) (for the homogeneous interface)

or (19.12) (for composite interface). According to their analysis, spreading of a liq-

uid continues, until simultaneously the (19.5) (the Young equation) is satisﬁed lo-

cally at the triple line and the minimal surface condition is satisﬁed over the entire

liquid-air interface. The minimal surface condition states, that the sum of inversed

principal radii of curvature, R

and R

(mean curvature), is constant at any point,

and thus governs the shape of the liquid-air interface.

= const . (19.14)

The same condition is also the consequence of the Laplace equation, which relates

pressure change through an interface with its mean curvature.

Stability of the composite interface is an important issue. Even though it may be

geometrically possible for the system to become composite, it may be energetically

proﬁtable for the liquid to penetrate into valleys between asperities and to form the

homogeneous interface. Marmur [86] formulated geometrical conditions for a sur-

face, under which the energy of the system has a local minimum and the compos-

ite interface may exist. Patankar [109] pointed out that, whether the homogeneous

or composite interface exists, depends on the system’s history, i.e., on whether the

dropletwas formed at the surface or deposited.However, the above-mentionedanal-

yses do not provide with an answer, which of the two possible conﬁgurations, ho-

mogeneous or composite, will actually form.

Limitations of the Wenzel and Cassie Equations

The Cassie equation (19.8) is based on the assumption that the heterogeneous sur-

face is composed of well-separated distinct patches of diﬀerent material, so that

the free surface energy can be averaged. It has been argued also that when the size

1006 B. Bhushan et al.

of the chemical heterogeneities is very small (of atomic or molecular dimensions),

the quantity that should be averaged is not the energy, but the dipole moment of

a macromolecule [62], and (19.8) should be replaced by

(1+ cosθ)

= f

(1+ cosθ

)

+ f

(1+ cosθ

)

. (19.15)

Experimental studies of polymers with diﬀerent functional groups showed a good

agreement with (19.15) [130].

Later investigations put the Wenzel and Cassie equations into a thermodynamic

framework, however, they showed also that there is no one single value of the con-

tact angle for a rough or heterogeneous surface [66,83,86]. The contact angle can

be in a range of values between the receding contact angle, θ

rec

, and the advancing

contact angle, θ

adv

. The system tends to achieve the receding contact angle when

liquid is removed (for example, at the rear end of a moving droplet), whereas the

advancing contact angle is achieved when the liquid is added (for example, at the

front end of a moving droplet). When the liquid is neither added nor removed, the

system tends to have static or “most stable” contact angle, which is given approx-

imately by (19.5)–(19.10). The diﬀerence between θ

adv

and θ

rec

is known as the

“contact angle hysteresis” and it reﬂects a fundamental asymmetry of wetting and

dewetting and the irreversibility of the wetting/dewetting cycle. Although for sur-

faces with the roughnesscarefully controlled on the molecular scale it is possible to

achieve contact angle hysteresis as low as < 1

◦

[54], hysteresiscannot be eliminated

completely, since even the atomically smooth surfaces have a certain roughness and

heterogeneity. The contact angle hysteresis is a measure of energy dissipation dur-

ing the ﬂow of a droplet along a solid surface. A water-repellent surface should have

a low contact angle hysteresis to allow water to ﬂow easily along the surface.

It is emphasized that the contact angle provided by (19.5)–(19.10) is a macro-

scale parameter, so it is called sometimes “the apparent contact angle.” The actual

angle, under which the liquid-air interface comes in contact with the solid surface

at the micro- and nanoscale can be diﬀerent. There are several reasons for that.

First, water molecules tend to form a thin layer upon the surfaces of many materi-

als. This is because of a long-distance van der Waals adhesion force that creates the

so-called disjoining pressure [42]. This pressure is dependent upon the liquid layer

thickness and may lead to formation of stable thin ﬁlms. In this case, the shape of

the droplet near the triple line (line of contact of the solid, liquid and air, shown

later in Fig. 19.6) transforms gradually from the spherical surface into a precursor

layer, and thus the nanoscale contact angle is much smaller than the apparent con-

tact angle. In addition, adsorbed water monolayers and multilayers are common for

many materials.Second, evencarefully preparedatomically smooth surfaces exhibit

certain roughness and chemical heterogeneity. Water tends to cover at ﬁrst the hy-

drophilic spots with high surface energy and low contact angle [35]. The tilt angle

due to the roughness can also contribute into the apparent contact angle. Third, the

very concept of the static contact angle is not well deﬁned. For practical purposes,

the contact angle, which is formed after a droplet is gently placed upon a surface

and stops propagating, is considered the static contact angle. However, depositing

19 Lotus Eﬀect: Roughness-Induced Superhydrophobic Surfaces 1007

the droplet involves adding liquid while leaving it may involve evaporation, so it is

diﬃcult to avoid dynamic eﬀects. Fourth, for small droplets and curved triple lines,

the eﬀect of the contact line tension may be signiﬁcant. Molecules at the surface

of a liquid or solid phase have higher energy because they are bonded to fewer

molecules, than those in the bulk. This leads to the surface tension and surface en-

ergy. In a similar manner, molecules at the edge have fewer bonds than those at the

surface, which leads to the line tension and the curvature dependence of the surface

energy. This eﬀect becomes important when the radius of curvature is comparable

with the so-calledTolman’s length, normallyof the molecular size [3]. However, the

triple line at the nanoscale can be curved so that the line tension eﬀects become im-

portant [111]. The contact angle with accountfor the contact line eﬀect for a droplet

with radius R is given by cos θ = cosθ

+ 2τ/(Rγ

), where τ is the contact line

tension and θ

is the value given by the Young equation [28]. Thus while the contact

angle is a convenient macroscale parameter, wetting is governed by interactions at

the micro- and nanoscale, which determine the contact angle hysteresis and other

wetting properties (Table 19.1).

Range of Applicability of the Wenzel and Cassie Equations

Gao and McCarthy [53] showed experimentally that the contact angle of a droplet

is deﬁned by the triple line and does not depend upon the roughness under the bulk

of the droplet. A similar result for chemically heterogeneous surfaces was obtained

by Extrand [47]. Gao and McCarthy [53] concluded that the Wenzel and Cassie–

Baxter equations “should be used with the knowledge of their fault.” The question

remained, however, under what circumstances the Wenzel and Cassie–Baxter equa-

tions can be safely used and under what circumstances do they become irrelevant.

For a liquid front propagating along a rough two-dimensional proﬁle

(Fig. 19.4ab), the derivative of the free surface energy (per liquid front length), W,

by the proﬁle length, t, yields the surface tension force σ = dW/ dt = γ

−γ

.The

quantity of practical interest is the component of the tension force that corresponds

Table 19.1. Wetting of a superhydrophobic surface as a multiscale process [102,106]

Scale level Characteristic

length

Parameters Phenomena Interface

Macroscale Droplet

radius (mm)

Contact angle,

droplet radius

Contact angle

hysteresis

Microscale Roughness

detail (µm)

Shape of the

droplet, position

of the liquid-air

interface (h)

Kinetic eﬀects 3D solid

surface,

2D liquid

surface

Nanoscale Molecular

heterogeneity

(nm)

Molecular descrip-

tion

Thermodynamic

and dynamic

eﬀects

1008 B. Bhushan et al.

to the advancing of the liquid front in the horizontal direction for dx. This com-

ponent is given by dW/dx = (dW/dt)(dt/ dx) = (γ

−γ

)dt/dx. It is noted that

the derivative R

= dt/ dx is equal to Wenzel’s roughness factor in the case when

the roughness factor is constant throughout the surface. Therefore, the Young equa-

tion, which relates the contact angle with solid, liquid, and air interface tensions,

cosθ = γ

−γ

, is modiﬁed as [96]

cosθ = R

(

−γ

)

. (19.16)

The empirical Wenzel equation (19.6) is a consequence of (19.16) combined with

the Young equation.

Nosonovsky [96] showed that for a more complicated case of a non-uniform

roughness, given by the proﬁle z(x), the local value of r(x) = dt/ dx

= (1+ (dz/dx)

)

1/2

matters. In the cases that were studied experimentally by Gao

and McCarthy [53] and Extrand [47], the roughness was present (r > 1) under the

bulk of the droplet, but there was no roughness (r = 0) at the triple line, and the

contact angle was given by (19.6) (Fig. 19.4c). In the general case of a 3D rough

surface z(x, y), the roughness factor can be deﬁned as a function of the coordinates

r(x, y) = (1+ (dz/ dx)

+ (dz/ dy)

)

1/2

Whereas (19.6) is valid for uniformly rough surfaces, that is, surfaces with

r = const, for non-uniformly rough surfaces the generalized Wenzel equation is for-

mulated to determine the local contact angle (a function of x and y) with a rough

surfaces at the triple line [96]

cosθ = r(x,y)cosθ

. (19.17)

The diﬀerence between the Wenzel equation (19.6) and the Nosonovsky equa-

tion (19.17) in that the later is valid for a non-uniformroughness with the roughness

factor as the function of the coordinates. Equation (19.17) is consistent with the ex-

perimental results of the scholars, who showed that roughness beneath the droplet

does not aﬀect the contact angle, since it predicts that only roughness at the triple

line matters. It is consistent also with the results of the researchers who conﬁrmed

the Wenzel equation (for the case of the uniform roughness) and of those who re-

ported that only the triple line matters (for non-uniformroughness) (Table 19.2).

The Cassie equation for the composite surface can be generalized in a similar

manner introducing the spatial dependence of the local densities, f

and f

of the

solid-liquid interface with the contact angle, as a function of x and y,givenby

cosθ

composite

= f

(x, y)cosθ

+ f

(x, y)cosθ

, (19.18)

where f

+ f

= 1,θ

and θ

are contact angles of the two components [96].

The important question remains, what should be the typical size of rough-

ness/heterogeneity details in order for the generalized Wenzel and Cassie equa-

tions (19.17)–(19.18) to be valid? Some scholars have suggested that roughness/

heterogeneity details should be comparable with the thickness of the liquid-air

interface and thus “the roughness would have to be of molecular dimensions to

19 Lotus Eﬀect: Roughness-Induced Superhydrophobic Surfaces 1009

Table 19.2. Summary of experimental results for uniform and non-uniform rough and chem-

ically heterogeneous surfaces. For non-uniform surfaces, the results shown for droplets larger

than the islands of non-uniformity. Detailed quantitative values of the contact angle in various

sets of experiments can be found in the referred sources [96]

Experiment Roughness/

hydropobicity

at the triple

line and at

the rest of

the surface

Roughness

at the bulk

(under the

droplet)

Experimental

contact angle

(compared

with that at

the rest of

the surface)

Theoretical

contact

angle,

Wenzel/

Cassie

equations

Theoretical

contact

angle,

generalized

Wenzel/

Cassie

(19.17)–(19.18)

Gao and Hydrophobic Hydrophilic Not changed Decreased Not changed

McCarthy Rough Smooth Not changed Decreased Not changed

[53] Smooth Rough Not changed Increased Not changed

Extrand Hydrophilic Hydrophobic Not changed Increased Not changed

[47] Hydrophobic Hydrophilic Not changed Decreased Not changed

Bhushan Rough Rough Increased Increased Increased

et al. [22]

Barbieri Rough Rough Increased Increased Increased

et al. [6]

alter the equilibrium conditions” [7], whereas others have claimed that rough-

ness/heterogeneity details should be small comparing with the linear size of the

droplet [6, 16, 18,19, 66–69, 83]. The interface in our analysis is an idealized 2D

object, which has no thickness. In reality, the triple line zone has two characteristic

dimensions: the thickness (of the order of molecular dimensions) and the length (of

the order of the droplet size).

The apparent contact angle, given by (19.17)–(19.18), may be viewed as the re-

sult of averaging of the local contact angle at the triple line by its length, and thus the

size of the roughness/heterogeneity details should be small comparing to the length

(and not the thickness) of the triple line. A rigorous deﬁnition of the generalized

equation requires the consideration of several scale lengths. The length dx needed

for averaging of the energy gives the length over which the averaging is performed

to obtain r(x, y). This length should be larger than roughness details. However, it is

still smaller than the droplet size and the length scale at which the apparent contact

angle is observed (at which local variations of the contact angle level out). Since

of these lengths (the roughness size, dx, the droplet size) the ﬁrst and the last are

of practical importance, we conclude that the roughness details should be smaller

than the droplet size. When the liquid-air interface is studied at the length scale

of roughness/heterogeneity details, the local contact angle, θ

, is given by (19.6)–

(19.10). The liquid-air interface at that scale has perturbations,caused by the rough-

ness/heterogeneity, and the scale of the perturbations is the same as the scale of

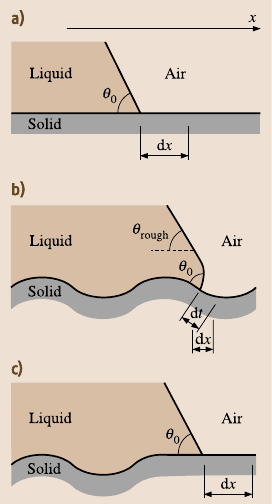
1010 B. Bhushan et al.

Fig. 19.4. Liquid front in contact with a (a) smooth

solid surface (b) rough solid surface, propagation

for a distance dt along the curved surface corre-

sponds to the distance dx along the horizontal sur-

face. (c) Surface roughness under the bulk of the

droplet does not aﬀect the contact angle

the roughness/heterogeneitydetails. However, when the same interface is studied at

a larger scale, the eﬀect of the perturbation vanishes, and apparent contact angle is

given by (19.17)–(19.18)(Fig. 19.4c). This apparent contact angle is deﬁned at the

scale length, for which the small perturbationsof the liquid-air interface vanish, and

the interface can be treated as a smooth surface. The valuesof r(x, y), f

(x, y), f

(x, y)

in (19.17)–(19.18)are average values bythe area (x, y) with size larger than a typical

roughness/heterogeneity detail size. Therefore, the generalized Wenzel and Cassie

equations can be used at the scale, at which the eﬀect of the interface perturbations

vanish,or,in otherwords,when thesizeof thesolid surfaceroughness/heterogeneity

details is small comparing with the size of the liquid-air interface, which is of the

same order as the size of the droplet.

Nosonovsky and Bhushan [106] used the surface energy approach to ﬁnd the do-

main of validity of the Wenzel and Cassie equations (uniformlyrough surfaces) and

generalized it for a more complicated case of non-uniform surfaces. The general-

ized equations explain a wide range of existing experimental data, which could not

be explained by the original Wenzel and Cassie equations.

19.2.3 Contact Angle Hysteresis

The contact angle hysteresis is another important characteristic of a solid-liquid

interface (Fig. 19.5a). The contact angle hysteresis occurs due to surface roughness

and heterogeneity. Low contact angle hysteresis results in a very low water roll-

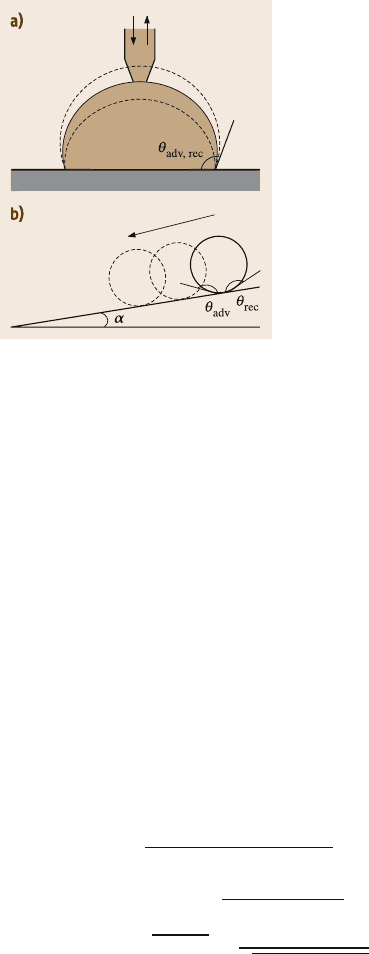
19 Lotus Eﬀect: Roughness-Induced Superhydrophobic Surfaces 1011

Fig. 19.5. (a) Liquid droplet in contact with rough

surface (advancing and receding contact angles are

adv

and θ

rec

, respectively) and (b) tilted surface

proﬁle (the tilt angle is α) with a liquid droplet

oﬀ angle, which denotes the angle to which a surface may be tilted for roll-oﬀ of

water drops (i.e., very low water contact angle hysteresis) [18, 19, 46,68, 69, 73]

(Fig. 19.5b). Low water roll-oﬀ angle is important in liquid ﬂow applications such

as in micro/nanochannels and surfaces with self cleaning ability.

There is no simple expression for the contact angle hysteresis as a function of

roughness; however, certain conclusions about the relation of the contact angle hys-

teresis to roughness can be made. Using (19.12), the diﬀerence of cosines of the

advancing and receding angles is related to the diﬀerence of those for a nominally

smooth surface, θ

adv0

and θ

rec0

, as [16,100]

cosθ

adv

−cosθ

rec

= R

(1− f

)(cosθ

adv0

−cosθ

rec0

)+ H

, (19.19)

where H

is the eﬀect of surface roughness, which is equal to the total perimeter of

the asperity per unit area. It is observed from (19.12) and (19.19), that increasing

→ 1 results in increasing the contact angle (cosθ →−1,θ → π) and decreasing

the contact angle hysteresis (cosθ

adv

−cosθ

rec

→ 0). In the limiting case of very

small solid-liquid fractional contact area under the droplet, when the contact angle

is large (cosθ ≈−1+ (θ−π)

/2, sinθ ≈π−θ) and the contact angle hysteresisis small

(θ

adv

≈ θ ≈ θ

rec

), (19.12) and (19.19) are reduced to

θ −π =



2(1− f

)(R

cosθ

+ 1) (19.20)

adv

−θ

rec

= (1− f

cosθ

−cosθ

sinθ





1− f



cosθ

−cosθ

√

2(R

cosθ

+ 1)

. (19.21)

For the homogeneous interface, f

= 0, whereas for composite interface f

is not a zero number. It is observed from (19.20)–(19.21) that for homogeneous

interface, increasing roughness (high R

) leads to increasing the contact angle hys-

teresis (high values of θ

adv

−θ

rec

), while for composite interface, an approach to