Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


5 Theory of Superconducting Alloys 207
Fig. 5.5. (a) Directions of arrows identify the ordinary and anomalous Green functions; (b)equationforallthreefunctions
generalizing the Dyson equation in Fig. 5.4 for the superconducting phase
i!
n
− −
¯
G(!
n
)
G (p; !
n
)
+
+
¯
F(!
n
)
F
†
(p; !
n
)=1,
i!
n
+ +
¯
G(−!
n
)
F
†
(p; !
n
)
+
∗
+
¯
F
†
(!
n
)
G (p; !
n
)=0, (5.17)
where
¯
G(!
n
)=
n
(2)
3
|U(p − p
)|
2
G(p
; !
n
)d
3
p
,
¯
F
†
(!
n
)=
n
(2)
3
|U(p − p
)|
2
F
†
(p
; !
n
)d
3
p
.
(5.18)
(and similarly for
F(!
n
)).
5.2.3 Properties of Homogeneous
Superconducting Alloys
In the absence of external electromagnetic fields and
currents the order parameter can be chosen to be
real, F(p; !
n
)=F
†
(p; !
n
), and the averages for the
isotropic model do not depend on p.Thesolutionof
the system of equations (5.17) is then given by
G(p; !
n
)=−
i ˜!
n
+
˜!
n
2
+
2
+ |
˜
(!
n
)|
2
,
F
†
(p; !
n
)=−
˜
(!
n
)
˜!
n
2
+
2
+ |
˜
(!
n
)|
2
,
(5.19)
with the notations
i ˜!
n
= i!
n
−
¯
G(!
n
);
˜
(!
n
)= +
¯
F
†
(!
n
) ,
and where we used the property
¯
G(−!
n
) ≡ −
¯
G(!
n
).
There are again contributions present in
¯
G(!
n
)
which are due to integration over farfromtheFermi
surface (the latter is defined by = 0). These con-
tributions do not depend on whether the system is
in the normal or superconductingstate and as before
will beincludedascorrections to thechemical poten-
tial.Withthis inmindweintegrateover inEq.(5.18)
in the symmetric interval ∈ (−L, L)around =0.
This gives
−
¯
G(!
n
)/i!
n
=
¯
F
†
(!
n
)/ (5.20)
and
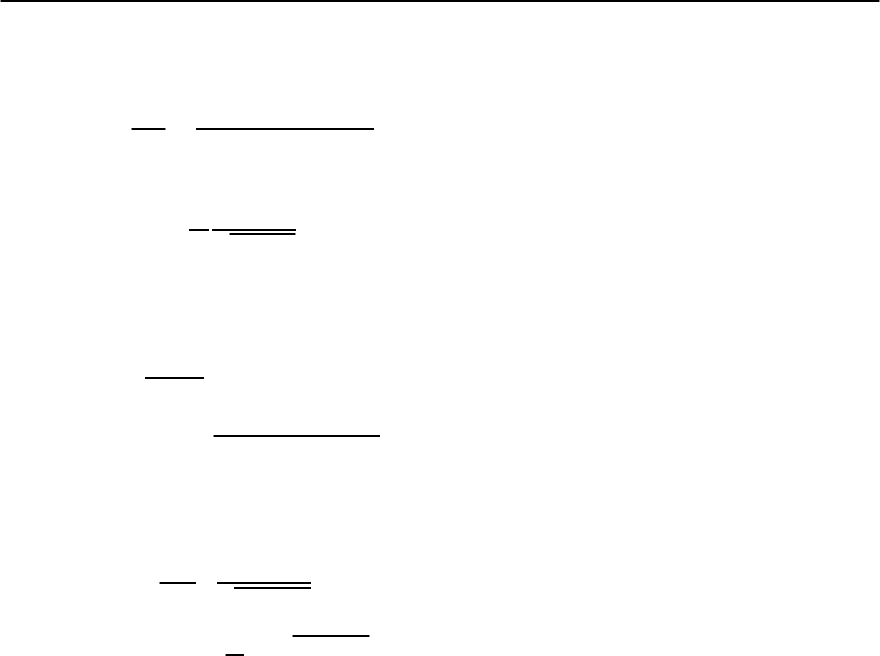
208 L.P. Gor’kov
i ˜!
n
= i!
n
!
n
,
˜
(!
n
)=
!
n
,
with
!
n
given by:
!
n
=1+
!
n
2
d
2
+(˜!
n
)
2
+ |
˜
(!
n
)|
2
.
Integration over gives
!
n
=1+
1
2
1
!
2
n
+
2
. (5.21)
The expression for the function F
†
(r − r
; !
n
)in
the coordinate representation (|r − r
| = R)canbe
written in terms of the above as
F
†
(R; !
n
)=−
i
(2)
2
R
(5.22)
×
pdp
e
ipR
−e
−ipR
2
!
n
2
+
!
2
n
+ ||
2
2
!
n
(after integration over the variables). Rewriting p as
p ≡ p
F
+ /v
F
and integrating over we easily ob-
tain
F
†
(R; !
n
)=
m
2R
cos p
F
R
!
2
n
+ ||
2
× exp
−
R
v
F
!
n
!
2
n
+ ||
2
.
From the expression for
!
n
it follows that the only
change in the spatial variation of F
†
(R; !
n
)(andof
the Green function G(R; !
n
)) is the appearance of
the multiplicative factor
exp(−R/2) (5.23)
(where = v
F
isthemeanfreepath).Inparticular,
it follows from the isotropic model for the average
gap that
¯
(r) ≡
0
, (5.24)
i.e., the gap remains thesameasfor a superconduc-
tor without defects or impurities. Since the thermo-
dynamics of a superconductor depends only on the
valueofthegap,onehastheimportantresultthat
the thermodynamics of homogeneous superconduc-
tors including the temperature of the superconduct-
ing transition T
c
is not changed by the presence of
defects,at least for lowenough defect concentrations.
This result was first obtained by A.A. Abrikosov
and L.P. Gor’kov in 1958 [1] and independently by
P.W. Anderson in 1959 [6] and is referred to in the
literature as “the Anderson theorem”. Strictly speak-
ing, the statement is correct for the isotropic model
only. For an anisotropic metal, as will be discussed
below,one may expect variationsof T
c
upon alloying.
Experimentally, in most superconductors of the“old
generation”, i.e. ordinary low temperature supercon-
ductors such as elemental metals, the Anderson the-
orem is satisfied with such a high accuracy that it is
often considered as an experimental test of whether
a superconductor belongs to the ordinary type. One
last comment is necessary to emphasize the range of
applicability of the above results: “low enough con-
centration” in practice means that one neglects any
terms of order 1/"
F
1orhigher.
5.3 Superconducting Alloys with a Small Gap
In this section we consider various applications of
the cross technique developed above. The technique
has its advantages and drawbacks. Among the latter
one may mention some awkwardness in carrying out
the calculations,especially for the intermediate con-
centrations where the mean free path is of the same
order as the coherence length
0
= v
F
/2T
c
(i.e., for
∼
0
). On the other hand, in many cases this tech-
nique allows one to use simple symmetry consider-
ations and to analyze different problems. Recall that
we neglect all diagrams with crossing dashed lines as
in Fig. 5.2(c). This fact will also allow us to derive the
so-called Eilenberger equations.The cross technique
is especially simple and transparent when applied to
problems where the superconducting order parame-
ter is small.
5.3.1 The Superconducting Transition Temperature
For a first application let us return again to the ques-
tion of whether the superconducting transition T
c
depends on the concentration of impurities n.This
time, however, we study a more general case, i.e. we
allow the impurity potential to depend on the spin
variables. Thus, in addition to the ordinary potential
energy U(r) of a single defect or impurity, for the

5 Theory of Superconducting Alloys 209
heavier elements the spin-orbit interactions would
also contribute to the scattering potential. We may
write this contribution as
ˆ
U
so
(r)=˛( ˆ ×∇U(r)) ·ˆp , (5.25)
where ˆp =−i∇ is the momentum operator and ˆ
standsfor the Pauli spin matrices.This interaction,of
course,preserves the time-reversal invariancefor the
electronic system as follows directly from Eq. (5.25)
upon substitution p → −p, → − .Atthesame
time scattering by so-called paramagnetic impuri-
ties, i.e. by magnetic centers with fixed local mo-
ments (spins) S, breaks the time-reversal symmetry
for the conduction electron subsystem ( ˆ → − ˆ
at t → −t). One may describe such scattering by a
potential
ˆ
U
p
(r)=U
p
(r)(S ·ˆ ) . (5.26)
The difference with respect to time reversal symme-
try between Eq. (5.25) and Eq. (5.26) has important
consequences.While spin-orbit interactions only af-
fect paramagnetic properties in the superconduct-
ing state, the presence of paramagnetic centers turns
out to be detrimental to superconductivity causing
new and rather nontrivial changes in the very na-
ture of the superconducting state such as the emer-
gence of so-called “gapless superconductivity”(A.A.
Abrikosov and L.P. Gor’kov, 1960 [7]).
In the momentumrepresentationthe potential de-
scribinga spin-orbit interaction Eq.(5.25) adds tothe
scattering amplitude
ˆ
f (p, p
)atermwhichweshall
write below in the following normalized form (for
the isotropic model)
ˆ
f
so
(p, p
)=iU
so
[p × p
] ·ˆ
p
2
F
.
To treat properly the spin-dependent contributions,
Eqs.(5.25) or (5.26), it is necessary to restore the spin
variables in all Green functions:
1
i!
n
− H
0
+ −
a
ˆ
U(r, r
a
)
2
×
ˆ
G(r, r
; !
n
)+
ˆ
(r)
ˆ
F
†
(r, r
; !
n
)=ı(r − r
) ,
1
−i!
n
− H
0
+ −
$
a
ˆ
U(r − r
a
)
&
∗t
2
×
ˆ
F
†
(r, r
; !
n
)−
ˆ
∗
(r)
ˆ
G(r, r
; !
n
)=0.
The notation [...]
∗t
in the second equation denotes
the hermitian conjugation together with permuta-
tion of the spin indices. As far as the value of the
transition temperature is concerned the problem is
linear in the gap . One is left with the second equa-
tion only where the normal state
ˆ
G(r, r
; !
n
)canbe
used. Assuming again
ˆ
†
(r) ≡
ˆ
†
together with the
self-consistency equation (5.15), one may write
ˆ
†
(r)=
g(r, r
)
ˆ
G
t
(r, l;−!
n
)
ˆ
G(l, r
; !
n
)
imp
×
ˆ
†
(l)d
3
ld
3
r
, (5.27)
where ...
imp
stands for the product of two Green
functions averaged over impurity positions. The in-
teraction kernel g(r, r
)inmostcasesbelowischosen
in its simplest “contact” form, with the exception of
Sect. 5.3.5, where the role of crystalline anisotropy in
the critical temperature T
c
is studied.
5.3.2 Ordinary I mp u rities
As a demonstration of the usefulness of Eq. (5.27), we
rederive the result that the temperature of the super-
conducting transition does not change upon alloying
with ordinaryimpurities.Simple analysisquitesimi-
lartothatwehavedonepreviouslyshowsthatinaver-
aging the product of two Green functions on the right
hand side of Eq.(5.27) one has to keep only diagrams
of the type shown schematically in Fig. 5.6(b,c). Di-
agrams of the first type result in the “exact” (normal
state) Green functions as given previously, while the
“ladder” diagrams in Fig. 5.6(c) must be summed up
with the same expression for the internal Green func-
tions.In the absence of spin effects the ,
†
matrices
in Eq. (5.27) are given as above . The self-consistency
equation (5.27) acquires the form shown in Fig. 5.7
with the vertex (p; !
n
) satisfying the equation for
the sum of all ladder diagrams in Fig. 5.6(c). Thus,
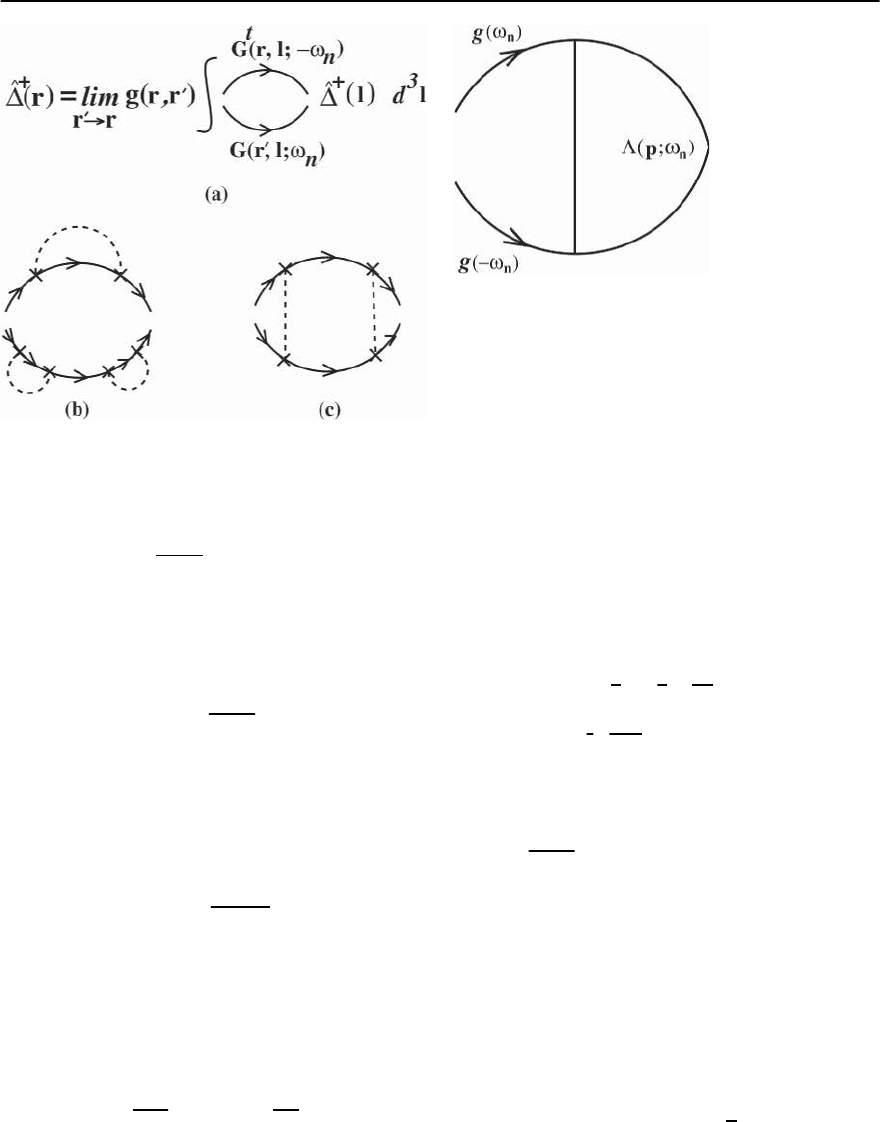
210 L.P. Gor’kov
Fig. 5.6. (a) Diagrammatic form of the linearized gap equa-
tion; (b) corrections to each of the two Green functions;
(c) “vertex” corrections
(p; !
n
)= +
n
(2)
3
|U(p − p
)|
2
(5.28)
× G(p
;−!
n
)G(−p
; !
n
)(p
; !
n
)d
3
p
and
= gT
!
n
d
3
p
(2)
3
G(p;−!
n
) (5.29)
× G(−p; !
n
)(p; !
n
) .
Performing the integrations over p and p
we obtain
for (p; !
n
)
(p; !
n
)=
1+
sign!
n
2!
n
, (5.30)
which exactly cancels the factor appearing in the ex-
pression in the denominator after integration of the
product of two Green functions. We thus return to
the familiar self-consistency equation which defines
T
c0
of a pure material
1=g
mp
F
2
2
2T
c0
n>0
1
!
n
. (5.31)
Fig. 5.7. Thevertexpartarisesasacontributionfromthe
“ladder” diagrams in Fig. 5.6(c)
The sum over frequencies !
n
in Eq. (5.31) diverges
which means that it must be supplemented by a cut-
off ˜! as usual.
5.3.3 Spin-Orbit Scattering
Consider now the contribution ofthe spin-orbit term
to the scattering processes shown in Fig. 5.6(b,c). Re-
peating all the arguments which have led us through
the analysis of the diagrams in Fig.5.2 and to the final
expression for the normal metal Green Function,itis
easy to verify that the spin-orbit interaction results
only in the substitution
1
⇒
1
+
1
so
, (5.32)
where 1/
so
=
2
3
nmp
F
(2)
2
|U
so
(p − p
)|
2
d§
p
(for the
isotropic model).Intheladderdiagrams inFig.5.6(c)
the spin-orbit term contributes to the dashed line
surrounding the matrix
ˆ
†
as
n
(2)
3
d
3
p
|U
so
(p − p
)|
2
(5.33)
×
i ˆ · [p × p
]
ˆ
†
i ˆ · [p × p
]
∗t
.
With the help of the identity
ˆg ˆ
t
ˆg =−ˆ , (5.34)
where ˆg is the metric tensor, the matrix equation
summing up all the ladder diagrams in Fig. 5.6(c)
reduces to the same equation (5.28) with the only
change being
|U(p − p
)|
2
⇒|U(p − p
)|
2
+
2
3
|U
so
(p − p
)|
2
,
5 Theory of Superconducting Alloys 211
i.e., to the renormalization of Eq. (5.32). Therefore,
the same cancellation takes place again as for defects
without the spin-orbit term. Thus, adding a spin-
orbit scattering amplitude does not change the ex-
pression for the the superconducting transition tem-
perature. Actually, reviewing our analysis above one
may easily verify that this result has a general char-
acter: the use of the identity Eq. (5.34) allows one
to rewrite a new equation (5.17) with the spin-orbit
contribution in the form of Eq. (5.32). This results in
the appearance of the multiplicative factor Eq.(5.23)
with the new mean free path . Therefore, the spin-
orbit contribution to scattering by defects does not
change the thermodynamics of the superconduct-
ing phase, although it may change dramatically the
spin susceptibility in the superconducting state (A.A.
Abrikosov and L.P. Gor’kov, 1962 [8]).
5.3.4 Paramagnetic Impurities
Let us now consider the concentration dependence of
the transition temperature in the presence of para-
magnetic impurities. In what follows we treat lo-
cal spins S at impurity sites such that the so-called
Kondo-effect (screening of the impurity spin by con-
duction electrons) is neglected; for a discussion of
the Kondo effect [9]. The exchange interaction in
Eq. (5.26) is usually weaker than scattering by the
ordinary potential (electrons forming local spins oc-
cupy an internal shell on the impurity center). As
for the Kondo effect, it is characterized by an energy
scale T
K
which is exponentially small in terms of the
exchange coupling U
p
(r). Therefore, T
K
is assumed
to be small compared to the temperature of the su-
perconducting transition, T
K
T
c
.
A straightforward calculation of the self-energy
diagram in Fig. 5.3 for the averaged normal Green
function again gives
G(p; !
n
)=
i!
n
− + isign!
n
/2
1
−1
,
where now 1/
1
=1/ +1/
s
and
1
s
=
nmp
F
(2)
2
S(S +1)
3
|U
p
(p−p
)|
2
d§
p
. (5.35)
(we have used for the local spins:
S
i
S
k
= S(S+1)ı
ik
/3).
However the exchange term Eq. (5.26) contributes
differently to the “ladder” diagrams in Fig. 5.6(c)
as follows from the presence of the Green function
ˆ
G
t
(r, l;−!
n
) in Eq. (5.27). Transferring the metric
tensor ˆg which defines the matrix structure of the
gap,
ˆ
†
across (S ˆ )
t
and again making use of the
identity Eq. (5.34) we arrive at a modified equation
(5.28) for the vertex function
p
(p; !
n
) in which, in-
stead of |U(p − p
)|
2
,onehas
|U(p − p
)|
2
⇒|U(p − p
)|
2
(5.36)
−
S(S +1)
3
|U
p
(p − p
)|
2
.
As a result, in an isotropic model where
p
(p; !
n
)=
p
(!
n
)wehave
p
(!
n
)=
!
n
+1/2
1
!
n
+1/
s
. (5.37)
Substitutionof Eq.(5.37) into Eq.(5.29) leads instead
of Eq.(5.31) to a new equation for the superconduct-
ing transition temperature T
c
:
1=
gmp
F
2
2
2T
c
n>0
1
!
n
+
1
s
. (5.38)
Combining Eq.(5.38) with Eq.(5.31),the latter defin-
ing the transition temperature T
c0
of the pure mate-
rial, it is not difficult to write down the following
equation for the dependence of the critical tempera-
ture T
c
on the concentration of paramagnetic centers
(A.A.AbrikosovandL.P.Gor’kov,1960[7])
ln
T
c0
T
c
=
1
2
+
2
−
1
2
, (5.39)
where =(T
c
s
)
−1
, (x) is the derivative of the
logarithm of the -function, and
1
2
+
2
−
1
2
=
n>0
1
n +1/2
−
1
n +1/2+/2
.
(5.40)
At low concentrations ( 1) T
c
decreases linearly
with concentration:
T
c
= T
c0
− /4
s
. (5.41)

212 L.P. Gor’kov
On the other hand, assuming that T
c
is small, 1,
and using the asymptotic form for the -function in
Eq. (5.40), one gets
T
2
c
=(6/
2
2
s
)ln(
s
T
c0
/2 ) . (5.42)
Equation (5.42) determines the critical concentra-
tion:
(1/
s
)
cr
=
T
c0
2
.
Above this concentration superconductivity is fully
destroyed by impurities (where ≈ 1.78 is the Euler
constant).
5.3.5 Impurities and Crystalline Anisotropy
The above non-trivial result for the concentration
dependence of the critical temperature in the pres-
ence of paramagnetic centers, was obtained under
the assumption of s-wave symmetry in calculating
averages over impurities in the Green function and
the vertex (p; !
n
) in Fig. 5.6(c). This immediately
raises the question aboutthe effect of impurities on a
superconducting state with a symmetry of the order
parameter other than the so-called“s-wave”pairing.
Sofarwehavefocusedontheisotropicmodel.In
this section we consider a more general case of an
anisotropic metal. In a crystal of a given the symme-
try density of states (p) is defined as
d
3
p
(2)
3
⇒
p
2
F
(p)
v
F
(p)(2)
3
dd§
p
≡
(p)d d§
p
4
and depends on the angular (or other) variables used
to define the position on the Fermi surface (,as
usual is the energy variable). At the same time (p)
remains invariant under all the transformations of
the point symmetry group. The same is true for
the pairing kernel g(r, r
), see Eq. (5.27). We already
know that in a weak coupling scheme superconduc-
tivity affects only states close to the Fermi surface.
Therefore, for the short ranged potential g(r, r
)it
is more convenient to use its corresponding form in
momentum space g(p, p
). The latter can be written
in the general form
g(p, p
)=
i,n
i
g
i
∗
i,n
i
(p)
i,n
i
(p
)
, (5.43)
where in the expansion Eq. (5.43) the functions
i,n
i
(p) represent a complete set of orthogonal eigen-
functions for the kernel g(p, p
) describing its de-
pendence on the Fermi surface variables. Indices i
denote functions transforming according to a rep-
resentation of the crystal symmetry group, while n
i
stands for the number of eigen functions belonging
to this representation in cases where a representa-
tion is degenerate. An essential difference relative to
theisotropicmodel,whereforall’s in Eq. (5.43)
we can use spherical harmonics, lies in the fact that
for a finite (point) crystalline group the number of
irreducible representations is also finite. Therefore,
in Eq. (5.43) functions
i,n
i
(p)and
j,n
j
(p)withi = j
transform according to the same representation of
the group.
Returning to the discussion of our impurity prob-
lem, we assume that in a given superconductor pair-
ing with the highest T
c0
corresponds to the choice
of one of these constants, say g
i
0
, so that the order
parameter (p) is of the form
(p)=
0
(T)
i
0
(p) . (5.44)
Its transformation properties are determined by
those of
i
0
(p). For calculating the averaged normal
Green function one can readily repeat all the steps
which have led to the previous equations with the
only difference that crystalline anisotropy is explic-
itly present in the momentum dependence of all pa-
rameters
1
1
(p)
=
n
(2)
2
|U(p, p
)|
2
(p
)dS
p
, (5.45)
where the integration is over the Fermi surface. The
function (p
) under the integral sign transforms ac-
cording to the identity representation and so does
1/
1
(p). Turning now to the calculation of the “lad-
der” diagrams, one sees that generally speaking a
new “scattering time” appears due to the integral in
Fig. 5.6(c), which has the form
1
2
(p)
=
n
(2)
2
|U(p, p
)|
2
(p
)
i
0
(p
)dS
p
.
Thus, for instance, if
i
0
(p
) does not belong to the
identity representation (as with the so-called “d-
wave” in cuprates), 1/
2
(p) differs drastically from

5 Theory of Superconducting Alloys 213
1/
1
(p) in Eq.(5.45).Hence,the results of ouranalysis
for paramagnetic impurities apply: superconductiv-
ity for the case of any phase with a non-trivial order
parameter is already reduced by the presence of or-
dinary defects. Note, in addition, that even if
i
0
(p
)
belongs to an invaria nt (identity) representation,the
above two integrals are not equal. From this point
of view the“Anderson theorem”is an approximation
which works better for a reasonably weak anisotropy
of (p).Experimentally itis fulfilledsurprisinglywell
in most of traditional superconductors.
The isotropic BCS model also displays the well
known square-root singularity in the density of
states,
S
(E), in the superconducting state
S
(E)
N
(E)
=
1
0, |E| <
/(E
2
−
2
)
1/2
, |E| >
. (5.46)
This singularity is seen explicitly in tunneling ex-
periments and was crucial for the explanation of the
well-known Hebel–Slichterpeak (L.C.Hebel and C.P.
Slichter, 1957 [10]) in the NMR-relaxation time, T
−1
1
near T
c
in ordinary superconductors. Observation
of this phenomenon by Hebel and Slichter in 1957
was initially taken as the ultimate proof of the cor-
rectness of the BCS-theory. Since then, the nature of
the superconducting order parameter is often judged
by whether the Hebel–Slichter peak is observed in a
given material or not, or whether the critical transi-
tion temperature is sensitive to the presence of de-
fects. Nevertheless, one should be aware that exces-
sive anisotropy, both in the normal properties and
in the gap, (p), may smear out the BCS singularity
Eq. (5.46) and be responsible for the sensitivity of T
c
to impurities, even if the gap has no nodes.
5.3.6 Ginzburg–Landau Equations
for Superconducting Alloys
Among other situations involving a small order pa-
rameter ((p)and
†
(p)), we will briefly discuss the
derivation of the Ginzburg–Landau (GL) equations
for superconducting alloys (L. P. Gor’kov, 1960 [11])
and the dependence of the critical field, H
c2
(T), on
temperature in the so-called “dirty-limit” (
0
)
(K. Maki, 1964) [12].
Equations for the order parameter in the pres-
ence of magnetic fields and the GL-functional near
T
c
were obtained microscopically for pure supercon-
ductors by L. P. Gor’kov in 1959 [13]. The derivation
in the presence of defects or impurity atoms begins
again by expanding the anomalous Green function
F
†
(r, r
; !
n
) in the self-consistency equation (5.15)
in powers of (r),
∗
(r). This is done with the help
of equations (5.14),andapplying the cross-technique
to average different terms over defects. To maximally
simplify our discussion, the expansion of ’s is first
shown schematically in Fig. 5.8(a). Recall that the or-
der parameter is self-averaged. Therefore, the terms
containing (r),
†
(r)inFig.5.8(a)onlytheslow
spatial variation caused (near T
c
) by the presence
of weak external fields, (i.e a non-zero A(r), where
A(r) is the vector potential of the magnetic field).
Themagnetic field dependence of each of thenormal
Green functions in Fig. 5.8(a) can be explicitly writ-
ten by making use of the quasi-classical character of
electron motion in metals (p
F
0
(T) 1, p
F
1)
(L. P. Gor’kov, 1959, 1960 [13,14]):
G(r, r
; !
n
) ⇒ exp
⎧
⎨
⎩
ie
c
r
r
A(l)dl
⎫
⎬
⎭
G(r, r
; !
n
) . (5.47)
While Eq. (5.47) has a general character and is ap-
plicable at all temperatures (L. P. Gor’kov, 1960 [14])
near T
c
it can be expanded in the phase factor, since
the critical magnetic field is small (H ∝ 1−T/T
c
).
The spatial dependence of the Green function, on
R = |r − r
|,isgovernedeitherby
0
= v
F
/2T
c0
or
bythemeanfreepath. Recall that the GL-equation
for the order parameter (r), which is proportional
to (or
†
for
†
) (L. P. Gor’kov, 1959), is a second
order differential equation, quadratic in the opera-
tor
ˆ
@ =(−i∇ −
2e
c
A). The phase factors guarantee
a gauge-invariant form of the operator
ˆ
@ (note we
have a charge 2e for the wave function of the Cooper
pair!).
After these preliminary remarks, it is a straight-
forward task to determine the coefficients in the GL
expansion for alloys. First, since the equations must
be gauge-invariant, i.e., include the gradient and the
vector potential A only in the combination defined
by the operator
ˆ
@, for the purpose of determining
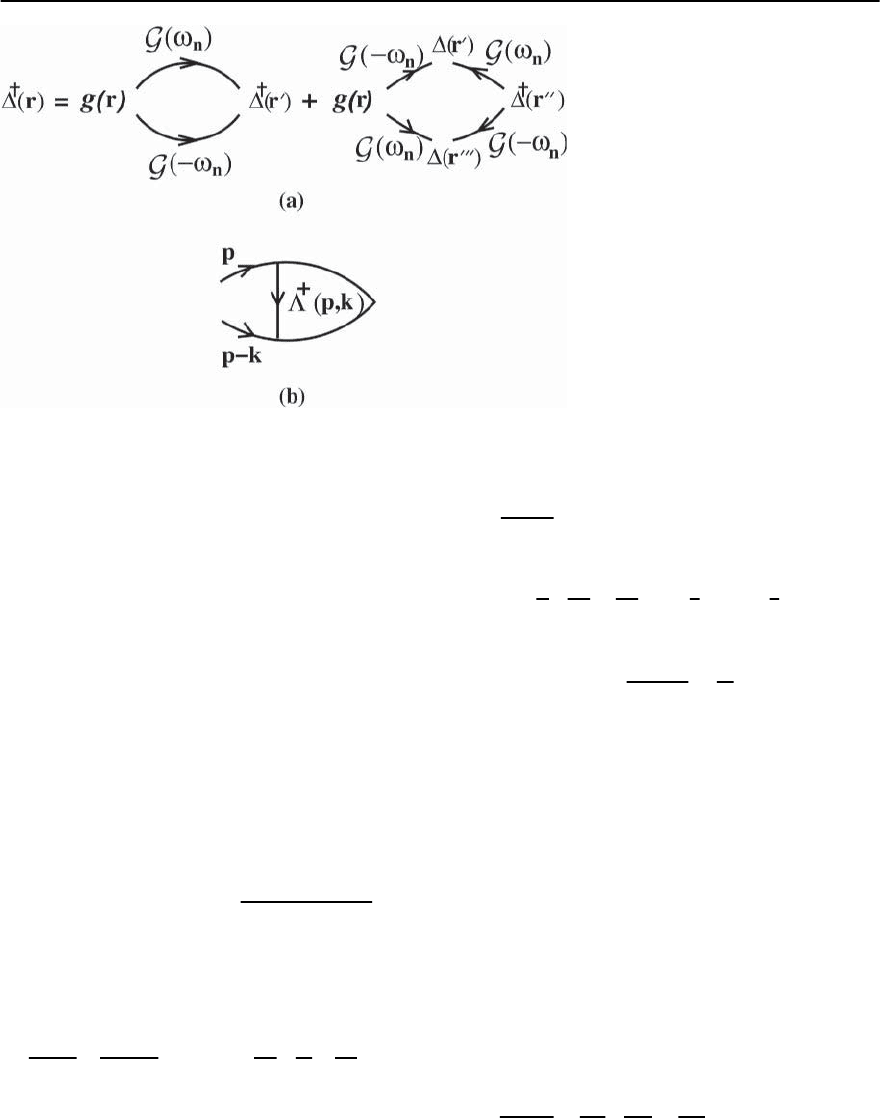
214 L.P. Gor’kov
Fig. 5.8. Expansion of the self-consist-
ency equation for
†
(r) up to third or-
der terms; (b) spatial dependence,
†
(r)
comes through the k-dependence in the
momentum representation
the coefficients one may omit the vector potential A
and consider only the spatial variation of (r)(or
†
(r)). It is more convenient to study the Fourier
transform, (k)(
†
(k)). Before proceeding further
with the cross-technique, let us recall that for a con-
stant (and
†
) the averaged anomalous functions,
F(r, r
; !
n
)andF
†
(r, r
; !
n
) coincide at r = r
with
their values in the absence of impurities.The transi-
tion temperature does not change and the third order
term in and
†
in Fig.5.8(a) (corresponding to the
bi-quadratic terms in the GL-functional)is the same
as for a GL-functionalof the pure superconductor. In
other words, almost everything is already known ex-
cept that it is necessary to recalculate the diagram in
Fig.5.8(b)(andthevertex,
†
(p, k; !
n
)) through sec-
ond order in k. As in Fig. 5.7 the vertex
†
(p, k; !
n
)
satisfies the equation
†
(p, k; !
n
)=
†
(k) + n
|U(p − p
)|
2
d
3
p
(2)
3
× G(p
;−!
n
)G(−p
+ k; !
n
)
†
(p
, k; !
n
) .
Expanding with respect to k we obtain for the GL
equation (L. P. Gor’kov, 1960 [11]):
1
T
c
− T
T
c
−
7(3)
8(T
c
)
2
| (r) |
2
+
2m
@
@r
−
2ie
c
A(r)
2
2
× (r)=0, (5.48)
where
=
2"
F
3
2
T
2
c
(5.49)
×
1
2
8
+
1
2
1
2
−
1
2
+
,
and
=
1
2T
c
tr
=
0
,
(here
tr
is the transport “collision” time). The first
two terms in Eq. (5.48) are the same as for a pure
superconductor.Asfor the third term, it significantly
changes the behavior of an alloy in a magnetic field.
As an illustration let us consider the problem of find-
ing the so-called“upper-critical field”B
c2
near T
c
for
superconductors of the second type (V. L. Ginzburg
and L. D. Landau, 1950 [15]; A. A. Abrikosov, 1957
[16]). To do this one may choose the Landau gauge
for the vector potential, A =(−By, 0, 0), in the lin-
earized equation (5.48).The latter then reduces to the
familiar harmonic oscillator equation defining the
shape of the nucleation center for the second-order
transition from the normal to superconducting state
in the presence of a magnetic field B
T
c
− T
T
c
+
2m
d
2
dy
2
−
4e
2
c
2
B
2
y
2
(y)=0.

5 Theory of Superconducting Alloys 215
Solving this equation we obtain
B
B
c2
=
T
c
− T
T
c
1
2
. (5.50)
The conclusion drawn from Eq. (5.50) is of a great
practical importance. Critical magnetic fields in-
crease dramatically for “dirty” alloys, i.e., for short
mean free path,
0
. Using the limit of
in
Eq. (5.49) for →∞and taking T = 0 in Eq. (5.50),
one can get an estimate for the limiting value of the
critical fields at low temperatures
B
B
c2
=
6
T
c
1
p
F
. (5.51)
Equation (5.51) makes sense, of course, only before
the Ioffe–Regel criterion p
F
∼ 1 signals the onset of
localization of the conduction electrons. Note, how-
ever, that close to this limit the critical field B
c2
that
is due to the mechanism of diamagnetic currents
reaches a point where one can no longer ignore the
paramagnetic effects (L. P. Gor’kov, 1963) [17]: the
spins of the two electrons comprising a Cooper pair
are oriented in opposite directions, while the mag-
netic field, via the Zeeman energy term
B
B ˆ ,tends
to align them along the field. Thus, the Zeeman en-
ergy itself results in breaking electron pairs. There-
fore,this leads at T = 0 to the so-called paramagnetic
limit (A.M.Clogston, 1962 [18]; B.S. Chandrasekhar,
1962) [19].
B
B
∗
cr
1.25T
c
.
Hence, in sufficiently“dirty” superconducting alloys
both the paramagnetic and diamagnetic effects must
be treated simultaneously (K. Maki and T. Tsuneto,
1964)[20].Letusalsomentionthat the anisotropy in-
herent in some layeredor otherwise low-dimensional
superconductors, in turn, may enhance the signifi-
cance of thePaulimechanisms (L.N.Bulaevskii,1974)
[21]. This subject, however, lies beyond the scope of
this chapter.
5.3.7 Upper Critical Field for ``Dirty Alloys´´
Returning to expression Eq. (5.50) for the critical
field, B
c2
,nearT
c
and to its estimate Eq. (5.51) for
dirty alloys at low temperature, we can show that in
the case of the isotropic model and of large concen-
trations of defects, impurities,
0
, the critical
field B
c2
(T) can actually be obtained in the frame-
work of the same technique for all temperatures T <
T
c
(K.Maki,1964 [12]).For this let us again consider
Fig. 5.7(b). In the product G(p;−!
n
)G(−p + k; !
n
)
one has for G(−p + k; !
n
)
G(−p + k; !
n
)=(i!
n
− + v
F
k + i/2)
−1
.
Near T
c
, v
F
k is small compared to !
n
∼ T
c
and 1/.
However, in the“dirty limit”case it is v
F
k 1/ ev-
erywhere below T
c
.This accordingto Eq.(5.51) yields
an estimate for the characteristic “magnetic length”,
a
H
=
√
c/eB (
0
)
1/2
. Therefore, for v
F
k one has
v
F
k ∼ (/
0
)
1/2
1 . (5.52)
As for the vertex
†
(p, k; !
n
) (formally it is of order
of unity) it becomes strongly renormalized(∼ 1/T
c
according to Eq. (5.30)). To proceed further with the
calculations, let us first integrate
G(p
;−!
n
)G(−p
+ k;−!
n
)
over the energy variable (d
3
p
⇒ mp
F
dd§
p
;the
integral over converges rapidly and one may as-
sume that
†
(p, k; !
n
) depends only on the momen-
tum at the Fermi surface). Then
†
(p, k; !
n
)=
†
(k) +
nmp
F
(2)
2
i
2
×
|U(p − p
)|
2
d§
p
(5.53)
×
(p
, k; !
n
)sign!
n
i!
n
+
i
2
sign!
n
+
v
F
k
2
.
Expanding using Eq. (5.53) in |!
n
|1, v
F
k 1/
in the denominator we arrive at the following equa-
tion:
†
(k)=
nmp
F
(2)
2
|U(p − p
)|
2
†
(p
, k; !
n
) (5.54)
×
=
−2!
n
+ i(v
F
k)sign!
n
−
2
(v
F
k)
2
>
d§
p
.
For the isotropic model Eq. (5.54) can be easily
solved in terms of the first two spherical harmon-
ics
†
(p
, k; !
n
)
†
0
(p
, k
2
; !
n
)+(v
F
k)
†
1
(p
; !
n
) .
(5.55)
216 L.P. Gor’kov
Thus,
†
1
(p
; !
n
)=isign!
n
2
tr
†
0
(p
; !
n
) , (5.56)
where the “transport time”
tr
is given by
1
tr
=
nmp
F
(2)
2
·
|U(p − p
)|
2
(1 − cos )d§
p
. (5.57)
After a short calculation we finally find
†
0
(p
, k
2
; !
n
)=
†
(k)
2
|!
n
| +
tr
k
2
v
2
F
6
−1
.
(5.58)
The next step would be to return to the real-space
representation using the correspondence k↔ − i∇
and the arguments given above in the derivation of
the GL-equation (5.48) with regards to the gauge
invariance. Correspondingly, we get k
2
⇒ (−i∇ −
2e
c
A(r))
2
. The eigenvalues of the latter operator in
the presence of a homogeneous magnetic field B are
well-known. Its lowest value, (2eB
c2
/c), determines
the upper critical fieldB
c2
(T) aftersubstituting equa-
tion (5.58) into the self-consistency equations (5.27).
Manipulations of formally divergent sums over !
n
,
which are quite analogous to those leading to equa-
tion (5.39), give the following equation from which
the temperature dependence B
c2
(T)canbeobtained
(K. Maki, 1964 [12]):
ln
T
c0
T
=
1
2
+ z
−
1
2
, (5.59)
where
z =
tr
v
2
F
eB
c2
(T)
6T
. (5.60)
For |T − T
c
|T we reproduce the result Eq. (5.50)
(
0
). Then at T → 0:
B
c2
(0) =
3
2
T
c0
e
tr
v
2
0.42
e
(
0
tr
)
−1
, (5.61)
in order-of-magnitude agreement with our estimate
Eq. (5.51) (note Eq. (5.60) and Eq. (5.61) are written
in units: =1,c =1).
5.4 Paramagnetic Alloys and Gapless
Superconductivity
In this section we discuss in more detail some
nontrivial properties of a superconductor contain-
ing paramagnetic impurities. In the (T, 1/
s
)-plane,
where 1/
s
∝ n characterizes the dependence on
impurity concentration, n, the phase boundary be-
tween normal and superconducting states is given by
equation(5.39).The criticalconcentration (1/
s
)
cr
0.88T
c0
limits the allowed concentration range for
the existence of superconductivity in such an alloy.
To analyze the thermodynamic properties below
the transition temperature, T
c
(n), it is necessary to
know the energy spectrum of the system. This in-
formation is contained in the Green functions of the
system. One can repeat all the steps in the deriva-
tion of the equations for the averaged Green func-
tions given before. The same equations result for
G(p; !
n
)andF
†
(p; !
n
) except that in the definitions
of i ˜!
n
= i!
n
−
¯
G(!
n
)and
˜
†
=
†
+
¯
F
†
(!
n
)one
needs to account for the different “collision” times
which according to Eq. (5.35) and Eq. (5.37) appear
now upon averaging two Green functions. Thus,
˜!
n
= !
n
+
1
2
1
u
n
u
2
n
+1
,
˜
n
= +
1
2
2
1
u
2
n
+1
, (5.62)
where1/
1
−1/
2
=2/
s
inaccordancewithEq. (5.35)
we defined the new variable
u
n
=
˜!
n
˜
(5.63)
which is an implicit function of the Matsubara fre-
quency
!
n
= u
n
1−
1
s
·
1
u
2
n
+1
%
. (5.64)
In a pure material the poles of the Green function on
the real frequency axis would directly determine the
quasi-particle energy spectrum and its dependence
on the momentum p.While the latter is not preserved
in the presence of scattering bydefects,theimportant
