Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

6 Impurity Nanostructures and Quantum Interference 237

Fig. 6.3. LDOS at r

1,2

as a function of energy for two im-

purities located at r

1,2

=(∓2, 0) with (a) JS/t =2.5, (b)

JS/t =2.7, and (c) JS /t =4.0. Results are obtained within

the BdG formalism

The first order phase transitions discussed above

are accompanied by a discontinuous change of the

(on-site) superconducting order parameter, 

1,2

,at

1,2

as shown in Fig. 6.4(a) where we plot the on-site

Fig. 6.4. On-site superconducting order parameter as a

function of JS for two impurities located at (a) r

1,2

(∓2, 0) with r =4,and(b) r

=(−1, 0) and r

=(2, 0)

with r = 3. Results are obtained within the BdG formal-

ism

order parameter as a functionof JS fortwoimpurities

located at r

1,2

=(∓2, 0). While the on-site order pa-

rameter changes discontinuously at (JS)

cr,1

,wefind

that in contrast to the case of a single magnetic im-

purity [11,24,60], it remains positive and does not

exhibit a -phase shift. Moreover, for JS > (JS)

cr,1

the superconductingorder parameter decreases con-

tinuously with increasing JS, and crosses zero at

JS/t ≈ 3.15. Interestingly enough, this zero-crossing

of the on-site order parameter does not lead to any

signature in the LDOS. Finally, we note that the sec-

ond first order transition at (JS)

cr,2

leads to an in-

crease in the magnitude of the superconducting or-

der parameter, in contrast to the transition at (JS)

cr,1

where the magnitude of the superconducting order

parameter decreases.

For all interimpurity distances we considered,the

dependence of the LDOS and the superconducting

order parameter on the scattering strength is simi-

lar to the one discussed above. However, the splitting

between (JS)

cr,1

and (JS)

cr,2

depends strongly on the

interimpurity distance. For example, for r =3,the

two phase transitions occur at (JS)

cr,1

/t =2.87 and

(JS)

cr,2

/t =2.9, as shown in Fig. 6.4(b). This split-

238 D.K.Morr

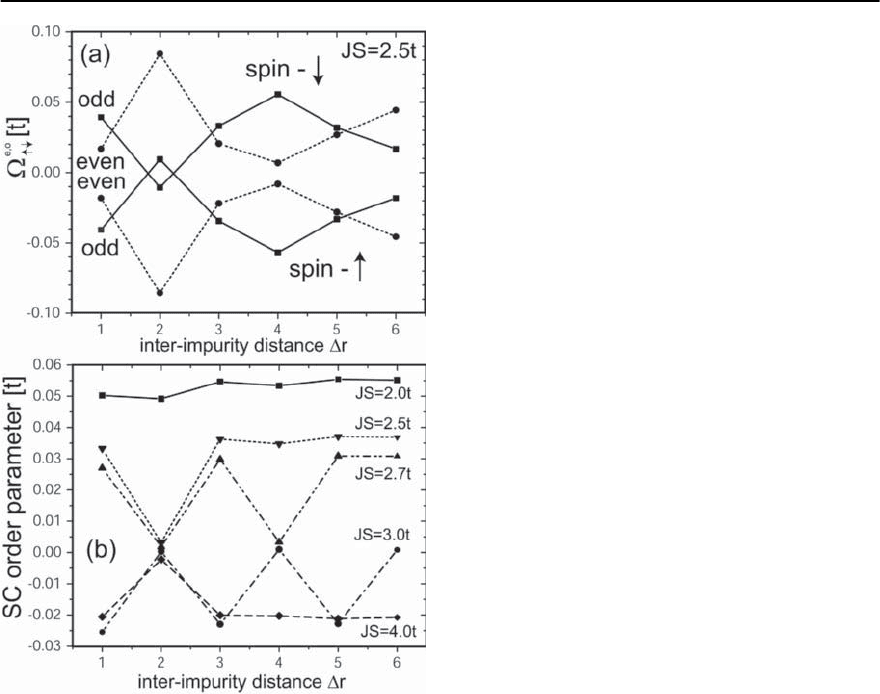
Fig. 6.5. (a) Frequency of the even and odd bound state

peaks as a function of interimpurity distance r for JS/t =

2.5. (b) Superconducting order parameter, 

1,2

at r

1,2

as a

function of interimpurity distance, r,forseveralvaluesof

JS/t. Results are obtained within the BdG formalism

ting between the two criticalvalues is thus consider-

ably smaller than that for the case r =4shownin

Fig. 6.4(a). In order to gain further insight into the

dependence of the critical values on the interimpu-

rity distance, r, we plot in Fig. 6.5(a) the frequency

of the even and odd bound state peaks as a func-

tion of r. As the distance between the two impuri-

ties is changed, the frequency of the even and odd

bound state peaks, as well as the splitting between

them oscillates [16,62]. The strength of the coupling,

D(r), between the impurity states can be directly

obtained from the frequency splitting between the

even and odd bound states, E = E

− E

=2D(r).

The results shown in Fig. 6.5(a) demonstrate that the

effective coupling between the impurity states does

not only vary in magnitude, but also changes sign

as the distance between the impurities is changed.

Specifically, we find from Fig. 6.5(a) that the split-

ting between the even and odd bound states is sig-

nificantly smaller for r = 3 than for r =4,im-

plying |D(r =3)| < |D(r =4)|. The smaller

value of D for r = 3 also explains the smaller split-

ting between the critical values (JS)

cr,1

and (JS)

cr,2

Note that the dependence of D(r)onr is deter-

mined by scattering processes involving both impu-

rities. Consider, for example, the wave function of an

electron that is scattered by the impurity at r

.The

sign and magnitude of its wave function at r

(and

hence those of D(r)) depend (a) on the distance be-

tween the impurities due to the (k

r)-oscillations of

the electronic wave-function, and (b) the scattering

phase shift at r

. Since the latter depends on JS,the

relative splitting between the even and odd bound

states also varies with JS, as further discussed below.

Note in particular that if the electron’s wave func-

tion vanishes at r

, the impurity bound states associ-

atedwith each of the two impurities cannot hybridize

and hence remain degenerate [16,62]. It also follows

from Fig.6.5(a)that when the interimpuritydistance

is changed from r =3tor =2,theoddbound

state crosses zero energy, signaling that the super-

conductor undergoes a first order quantum phase

transition in which its ground state spin polariza-

tion changes from S

 =0toS

 =−1/2. Hence,

changing the spatial locationof one of the impurities

gives rise to a phase transition ofthe entire supercon-

ductor. This transition is accompanied by a drastic

change in the on-site superconducting order param-

eter at r

1,2

, as shown in Fig. 6.5(b) where we plot

the order parameter as a function of interimpurity

distance for several values of JS.ForJS/t =2.5, the

on-site order parameter changes from 

1,2

=0.036t

at r =3to

1,2

=0.003t at r =2.Itisinter-

esting to note that when the interimpurity distance

is decreased even further from r =2tor =1,

another first order transition occurs, in which the

superconductor’s ground state polarization changes

6 Impurity Nanostructures and Quantum Interference 239

from S

 =−1/2toS

 =0.Thechangeinthe

superconductor’s ground state directly reﬂects the

dependence of (JS)

cr,1

on the interimpurity distance.

For r = 3, one finds (JS)

cr,1

/t > JS/t =2.5, im-

plying that the spin polarization of the supercon-

ductor is S

 = 0. In contrast, for r =2onehas

(JS)

cr,1

/t < JS/t =2.5 < (JS)

cr,2

/t,yieldingaground

state with S

 =−1/2.Thus as the interimpuritydis-

tance is monotonically decreased (or increased), the

superconductor can be tuned through several first

order transitions.This is the first example of a quan-

tum interference induced quantum phase transition

in impurity nanostructures. If JS is too small, how-

ever, (as, for example, in the case with JS/t =2),no

first ordertransition occurs,andthe order parameter

exhibits only weak Friedel-like oscillations when the

distance between the impurities is varied. For larger

JS (see, for example, JS/t =2.7), the number of first

order transitionsthat occur bychanging the interim-

purity distance increases. In all of these transitions,

the superconductor’s ground state changes between

states with S

 =0andS

 =−1/2. In contrast, for

JS/t =3.0, the superconductor still undergoes a se-

ries of phase transitions as r is varied, but now the

transitions occur between states with S

 =−1/2

and S

 =−1.WhenJS is increased even further,the

number of phase transitions decreases again (see,for

example, JS/t =4.0), since eventually JS > JS

cr,2

for

any r ≥ 1, implying that the superconductor is in a

ground state with S

 =−1.

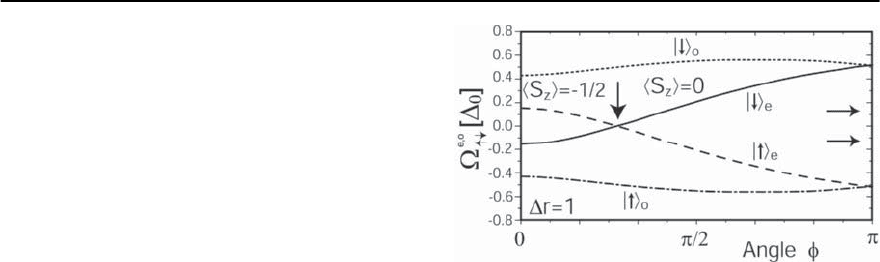
Finally, we note that the superconductor can also

be tuned through a quantum phase transition by

changing the relative angle, , between the two im-

purity spins, as shown in Fig. 6.6, where we plot

e,o

↑,↓

as a function of  for two impurities with

JS/

= 20 located at r

=(0, 0) and r

=(1, 0).

Since (JS)

cr,1

< JS < (JS)

cr,2

, the ground state for

 = 0 possesses a spin polarization S

 =−1/2.

As  increases from zero, the frequency of the even

bound state decreases and crosses zero at 

≈ 0.27

(indicated by an arrow in Fig. 6.6). This crossing

is accompanied by a first order phase transition in

which the spin polarization of the superconductor’s

ground state changes from S

 =−1/2 (for  < 

)

to S

 = 0 (for  > 

). The frequency separation

between the even and odd states decreases with in-

Fig. 6.6. §

e,o

↑,↓

as a function of the angle, , between the di-

rection of the impurity spins for r =1andJS/

= 20.

Results are obtained within the

T-matrix formalism

creasing  and vanishes at  = .Thisisexpected

since for antiparallel impurity spins ( = ), the

bound state for impurity 1 (consisting of |p, ↑, 1

and |h, ↓, 1)andimpurity2(|p, ↓, 2 and |h, ↑, 2)

possess different quantum numbers; thus they can-

not hybridize and remain degenerate.However,since

the bound state of one impurity is subjected to the

repulsive potential of the second impurity, their res-

onance frequencies are larger than those of a single

impurity with the same JS (indicated by the arrows

on the right). This repulsion leads to the disappear-

ance of all bound states for r → 0.

Finally, first quantum interference effects in su-

perconductors have recently been reported in STM

experiments by Derro et al. [63] in simple nanos-

tructures consisting of oxygen defect sites in the

one-dimensional (1D) CuO chains of the high-

temperature superconductor YBa

6+x

.Were-

cently argued [61, 91] that these effects are similar

to the quantum interference phenomena discussed

above for bulk s-wave superconductors. In particu-

lar, we showed that the superconducting gap which

emerges in the chains due to a proximity coupling to

the CuO

planes, possesses an s-wave symmetry.This

symmetry arises since due to the reﬂection symme-

try of the 1D chains one has (k

)=(−k

), where

is the Fermi momentum in the chains.We demon-

strated that quantum interference effects between

magnetic defects leads to the formation of antibond-

ingandbondingimpurity states in the chains,aresult

which is fully consistent with the experimentally ob-

240 D.K.Morr

served splitting between the bound state peaks in the

LDOS.

6.4.2 Quantum Corrals and Quantum Imaging in

s-wave Superconductors

As discussed in the introduction, Manoharan et

al. [48] recently demonstrated that quantum imag-

ing via electronic waves can be achieved in quantum

corrals that are placed on the surfaces of metals. In

this section, we investigate the possibility for new

quantum phenomena in quantum corrals located on

the surface of an s-wave superconductor.In general,

we expect that the non-trivial electronic correlations

arising from particle-hole mixing in the supercon-

ducting state affect the quantum imaging properties

of the quantum corral. In what follows,we again use

the fermionic bound state induced by a single mag-

netic impurity as the quantum candle whose spec-

troscopic signature in the LDOS can be quantum im-

aged. In order to study quantum interference effects

separately from the formation of fermionic impurity

states, we consider quantum corrals that consist of

non-magnetic impurities.

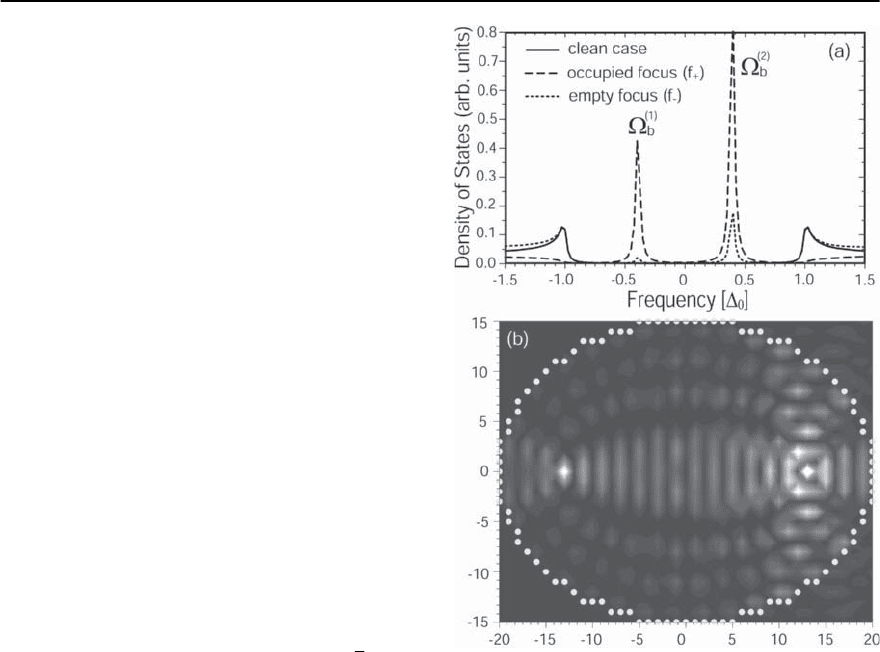
We begin our study of quantum imaging in super-

conductors by considering an elliptical corral with

semi-axesa = 20,b = 15 (eccentricity e =

√

7/4) that

consists of 100 non-magnetic impurities. A magnetic

impurity is located in thecorral’sfocus at f

=(13, 0),

while the other focus at f

−

=(−13, 0) is left empty

(the center of the corral is located at (0, 0)). The

fermionic bound state induced by the magnetic im-

purity possesses a particle-like and hole-like peak

in the LDOS at frequencies §

(1,2)

/

= ∓0.4as

shown in Fig.6.7(a). Note that in the absence of mag-

netic impurities,no eigenmodes exist for frequencies

|!| < 

, i.e., inside the superconducting gap. How-

ever,the bound state excites an eigenmode of the cor-

ral inside the superconducting gap,leading to spatial

oscillations in the LDOS, as shown in Fig. 6.7(b) for

! = §

(2)

.This eigenmode,in turn,creates a quantum

image (in the LDOS) of the bound state peaks in the

empty focus at f

−

(Fig.6.7a) [86].The presence of two

peaks in the LDOS at §

(1,2)

permits us to study eigen-

modes at different excitation energies. It was noted

earlier [52], that eigenmodes can only be excited if

Fig. 6.7. (a) LDOS in the occupied (dashed line)andempty

focus (dotted line) for a non-magnetic corral with a mag-

netic impurity located at f

. Solid line:LDOSoftheclean

system. (b) Spatial plot of the LDOS inside the quantum

corral (the filled yellow circles represent the corral impu-

rities) at §

(2)

/

=0.4. Results are obtained within the

T-matrix formalism

the excitation (via the impurity bound state) takes

place at a position where the spectral weight of the

eigenmode is large, and if the excitation energy, i.e.,

(1,2)

, is close to the eigenmode’s energy (note that

due to the corral wall’s porosity and its finitescatter-

ing potential, the eigenmodes possess a substantial

frequency width [52]). While two eigenmodes exist

outside the superconducting gap at §

(±)

/

= ±1.1,

the mode’s amplitude at §

(+)

in the vicinity of the

foci is considerably larger than that at §

(−)

, yielding

a weaker eigenmode, a weaker quantum image and

a concentration of spectral weight around f

at §

(1)

6 Impurity Nanostructures and Quantum Interference 241

We thus conclude that an impurity bound state can

excite eigenmodes inside the superconducting gap,

which in turn can be used for creating quantum im-

agesoftheboundstatepeaks[86].

The ability of the corral to form a quantum im-

age of the quantum candle strongly depends on the

ratio of the decay length, 

= 



1−(§

/

)

and the corral’s semi-axes, a and b.For

 a, b

the bound state wave-function at the position of the

corral wall is exponentially suppressed, no eigen-

modes can be excited, and the spatial form of the

LDOS at the frequency of the impurity bound state

remains unaffected by the presence of a quantum

corral. In contrast, for the case shown in Fig. 6.7, one

has 

=16.4  a, b and the spatial LDOS pat-

tern at §

(2)

is strikingly different for a single mag-

netic impurity at f

with and without a corral. Note

also that the presence of a corral shifts §

(1,2)

from

(1,2)

/

= ±0.575 (no corral) to §

(1,2)

/

= ±0.4

which is a qualitatively new feedback effect of the

corral on the impurity bound state.

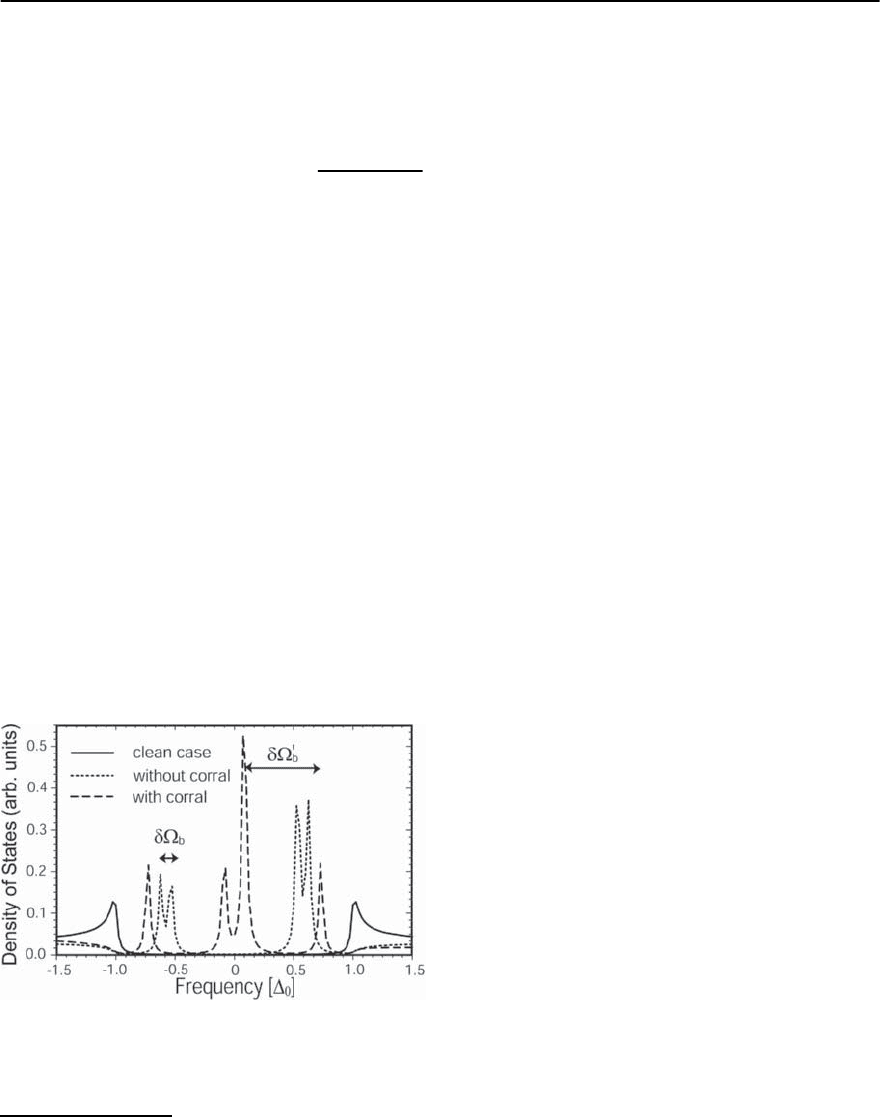
As discussed in Sect. 6.4.1 quantum interference

effectsbetween two magnetic impurities in an s-wave

superconductor lead to a frequency splitting of the

bound state peaks through the formation of bonding

and antibonding bound states [16,62].This splitting,

which is a direct measure of the interaction between

the impurities, can be enhanced if the magnetic im-

Fig. 6.8. Splitting of the bound state peaks in the LDOS

at f

−

= (−13, 0) with and without a quantum corral for

two magnetic impurities with parallel spins. Results are

obtained within the

T-matrix formalism

purities are placed in the foci of a corral, as shown in

Fig.6.8.We consider the corral of Fig.6.7 and assume

for definiteness that the impurity spins are parallel,

however,qualitativelysimilar resultsare obtainedfor

arbitrary angle between the spins. In the absence of

a quantum corral, the splitting of the bound state

peaks is small, ı§

/

=0.1,duetothelargedis-

tance between the impurities.However,when the two

impurities are located inside a quantum corral, the

splitting increases to ı§



/

=0.65, implying that

the interaction between the two magnetic impurities

is enhanced. This splitting therefore provides a di-

rect probe forthe strength of the interactionbetween

magnetic impurities [86]. Our results thus demon-

strate that quantum corrals provide new possibilities

for manipulating the interaction between magnetic

impurities.

Based on the results shown above, the question

naturally arises whether quantum corrals can also be

employed for the simultaneous creation of multiple

quantum images. To study this question, we consider

a triangular equilateral quantum corral consisting of

90 non-magnetic impurities with U

=4eV,asshown

in Fig. 6.9 (the impurities, represented by filled yel-

low squares, are separated by r =2).Motivatedby

recent experiments by Braun and Rieder [49], who

studied triangular quantum corrals on the surface

of Ag, we consider a 2D host system with a triangu-

lar lattice

(lattice constant a

= 1) and dispersion



= k

/2m −  ( =1)with =−65meVand

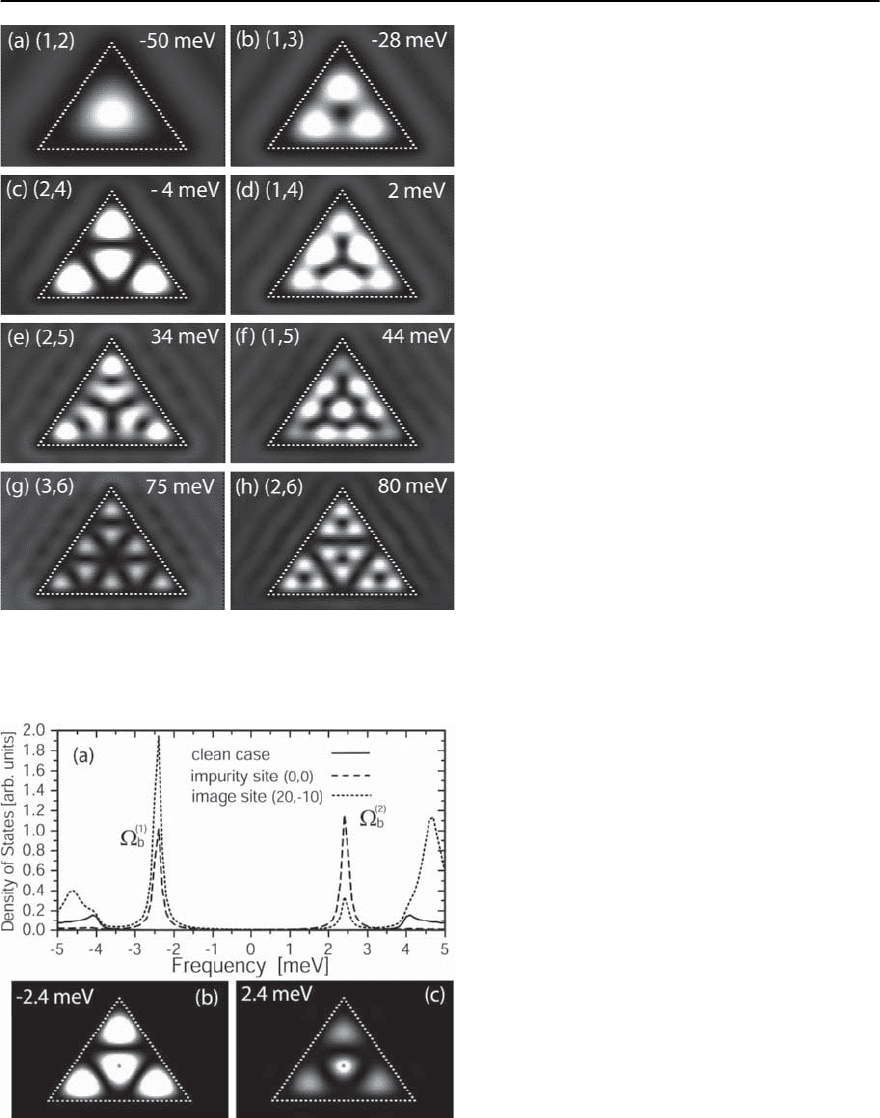
=0.24. In Fig. 6.9(a)-(h), we present a spatial plot

of the LDOS at the frequencies of the eight lowest

energy eigenmodes in the normal state [87]. In the

unitary scattering limit considered here, the eigen-

modes (i.e., their spatial structure and ordering in

energy) are well described by the eigenstates, 

of an infinitelydeep triangular potential well (TPW)

[92] [the corresponding quantum numbers (m, l)are

shown in the upper left corner of Figs. 6.9(a)-(h)].

It is the spatial form of the corral’s low-energy

eigenmodes that opens the possibility to project mul-

tiple quantum images in the superconducting state.

To demonstrate this novel quantum effect, we as-

sume that the host system is an s-wave supercon-

ductor with gap 

= 4 meV, yielding a supercon-

All coordinates given in the following are those of a triangular lattice.

242 D.K.Morr

Fig. 6.9. (a)–(h) Spatial plot of the LDOS at the frequen-

cies of the eight lowest energy eigenmodes of a trian-

gular corral (eigenmode energy is shown in the upper

right corner) in the unitary scattering limit (U

= 4 eV).

(m,l) are the quantum numbers of the correspond-

ing TPW eigenstate. Results are obtained within the

T-matrix formalism.

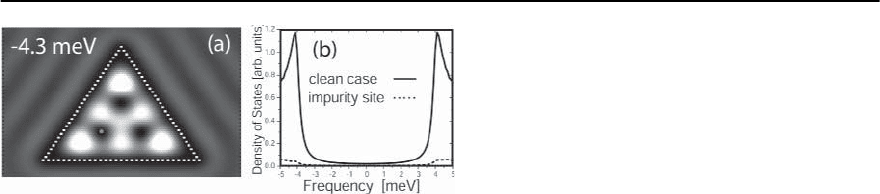
Fig. 6.10. (a) LDOS as a function of frequency. (b),(c)

Spatial plot of the LDOS at the bound state energies

(1,2)

= ∓2.4 meV, respectively. Results are obtained

within the

T-matrix formalism

6 Impurity Nanostructures and Quantum Interference 243

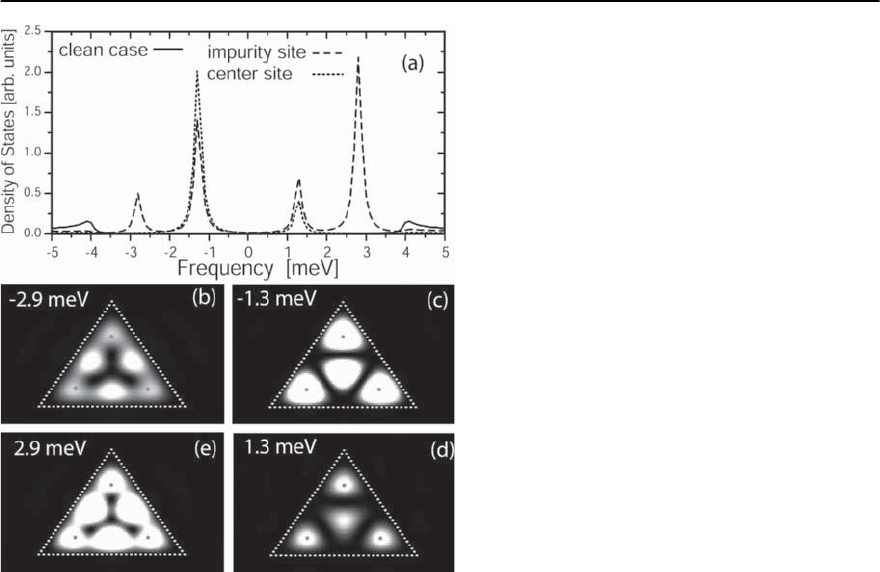
Fig. 6.11. (a) Spatial plot of the LDOS for |!| > 

.(b)

LDOS at the site of the magnetic impurity. Results are

obtained within the

T-matrix formalism

ducting coherence length 

= k

/(m

) = 135,and

place a single magnetic impurity (JS =1.0eV)in

the center of the triangular corral at r

=(0, 0). The

particle-like and hole-like peak in the LDOS of the

impurity induced bound state are located at ener-

gies §

(1,2)

= ∓2.4 meV, as shown in Fig. 6.10(a). In

Figs. 6.10(b) and (c) we present spatial plots of the

LDOS at §

(1,2)

(the locationof the magnetic impurity

is shown as a filled red circle). The formation of the

impurity bound state is accompanied by the excita-

tion of the (2, 4)-eigenmode [Fig. 6.9(c)] and by the

emergence of three images of the bound state peaks

inside the corral. As already discussed above, only

eigenmodes that possesses sufficiently large spectral

weight at the impurity site and are close in energy

to §

(1,2)

are relevant for the formation of quantum

images. Since the energy of the (2, 4)-eigenmode,

(2,4)

=−4meV,iscloserto§

(1)

thanto §

(2)

,thespec-

tral weight of the quantum images is larger at §

(1)

than at §

(2)

, as follows directly from a comparison

of Figs. 6.10(b) and (c). Note that the spatial pattern

of the quantum images can be“custom designed”by

shifting the eigenmode energies via changes in the

corral’s size [92]. For example, in a triangular corral

consistingof 117 impurities,the spatialpattern of the

quantum images in the superconducting state is de-

termined by the (1, 5)-mode [Fig.6.9(f)]since in this

case E

(1,5)

= 0 meV. The above results demonstrate

that by choosing an appropriate geometry and size

of a quantum corral,it is possible to custom design a

corral’s imaging properties,and,as discussed here,to

create multiplequantum images at specific locations.

As discussed above,magnetic impurities in s-wave

superconductors are pairbreaking, and thus lead to

the formation of impurity bound states inside the su-

perconducting gap[3,5–7].We find,however,thatthis

fundamental property of a magnetic impurity can be

reversed inside a quantum corral,leading to the com-

plete suppression of the impurity bound state [87].

To demonstrate this effect, we place the magnetic

impurity at a node [r

=(−5, −5)] of the (2, 4)-

and (1, 4)-eigenmodes, as shown in Fig. 6.11(a) (the

LDOS is shown at |!| > 

). We find that in the

superconducting state, no bound state is induced by

the magnetic impurity, as follows from the plot of

the LDOS at r

shown in Fig. 6.11(b), and hence, no

image is observed anywhere inside the corral. This

complete suppression arises from the incompatibil-

ity of the bound state with the boundary conditions

provided by the corral’s wall. In other words, an im-

purity bound statecan only be formed ifit can couple

to one of the corral’s eigenmodes. The importance of

this result lies in the fact that while non-magnetic

impurities cannot induce a fermionic bound state in

an s-wave superconductor,they can suppress its for-

mation and thus reverse the pair-breaking effect of a

magnetic impurity.

To further study the interplay between the cor-

ral’s imaging properties, its geometry and the lo-

cations of the quantum candles, we next consider

the case of three magnetic impurities with paral-

lel spins that are located at the corners of an equi-

lateral triangle at r

=(−10, −10), r

=(20, −10),

and r

=(−10, 20). Since the degeneracy of the im-

purity bound states is lifted via quantum interfer-

ence, we expect to find six peaks in the LDOS. In-

stead, the LDOS exhibits only four peaks, as shown

in Fig. 6.12(a), corresponding to the presence of only

two non-degenerate impurity states. This reduction

to two impurity states arises from a new type of op-

tical selection rule that is based on the interplay be-

tween the corral geometry and the location of the

quantum candles. Under a rotation of 2/3around

244 D.K.Morr

Fig. 6.12. (a) LDOS as a function of frequency. (b)–(d)

Spatial plot of the LDOS at the frequency of the impu-

rity bound state with n =2[(b)and(e)] and n =0[(c)

and (d)]

the corral’s center, 

, and hence the corral eigen-

modes, transform as 

→ exp[i2(m + l)/3]

Due to the impurities’geometry the non-degenerate

impurity bound states possess the same transforma-

tion properties. Hence, the formation of three hy-

bridized bound states requires that they couple to

eigenmodes with n =(m + l)mod3 = 0, 1, 2. How-

ever, the eigenmodes with n =1areatenergies

(m,l)

|

, thus preventing the creation of the hy-

bridized bound state with n = 1. As a result, only the

bound states with n = 0 [Figs. 6.12(c) and (d)] and

n = 2 [Figs.6.12(b)and (e)]are formedvia their cou-

pling to the (2, 4)- [Fig.6.9(c)]and(1, 4)-eigenmodes

[Fig. 6.9(d)], respectively.

To summarize,we find thatthe combination of im-

purity nanostructures and s-wave superconductors

leads to the emergence of a series of novel quantum

phenomena, ranging from the creation of multiple

quantum images and novel optical selection rules, to

the suppression of pairbreaking effects and quantum

interference induced first order phase transitions.

6.5 Quantum Interference Phenomena in

−y

2 -wave Superconductors

In d

−y

-wave superconductors, novel quantum in-

terference phenomena arise from the interplay be-

tween the momentum dependence of the d

−y

-wave

superconductinggap,thegeometry ofthenanostruc-

ture and its orientation with respect to the lattice.

For the results presented below, we take the normal

state tight-binding dispersion of the cuprate super-

conductors [93] to be of the form

=−2t



cos k

+cosk



−4t



cos k

−  ,

(6.22)

with t = 300 meV, t



/t =−0.4, and /t =−1.18, and

the maximum superconducting gap to be given by



=25meV.

Before studying more complex impurity struc-

tures,we start by investigating quantum interference

phenomenain nanostructuresconsisting oftwo non-

magnetic impurities. This simple system allows us to

6 Impurity Nanostructures and Quantum Interference 245

Fig. 6.13. LDOS at r

1,2

as a function of frequency and r for

two non-magnetic impurities with U

= 700 meV located

at r

=(0, 0) and r

=(r, 0). Results are obtained within

the

T-matrix formalism

gainfirst insight into the dependence of quantum in-

terference effects on the interimpurity distance and

the relative orientation of the two impurities with

respect to the underlying lattice. To investigate the

former, we consider two impurities with scattering

potential U

1,2

= U

= 700 meV (corresponding to the

unitary limit [9,12]) that are located along the crys-

tal ˆx-axis at r

=(0, 0) and r

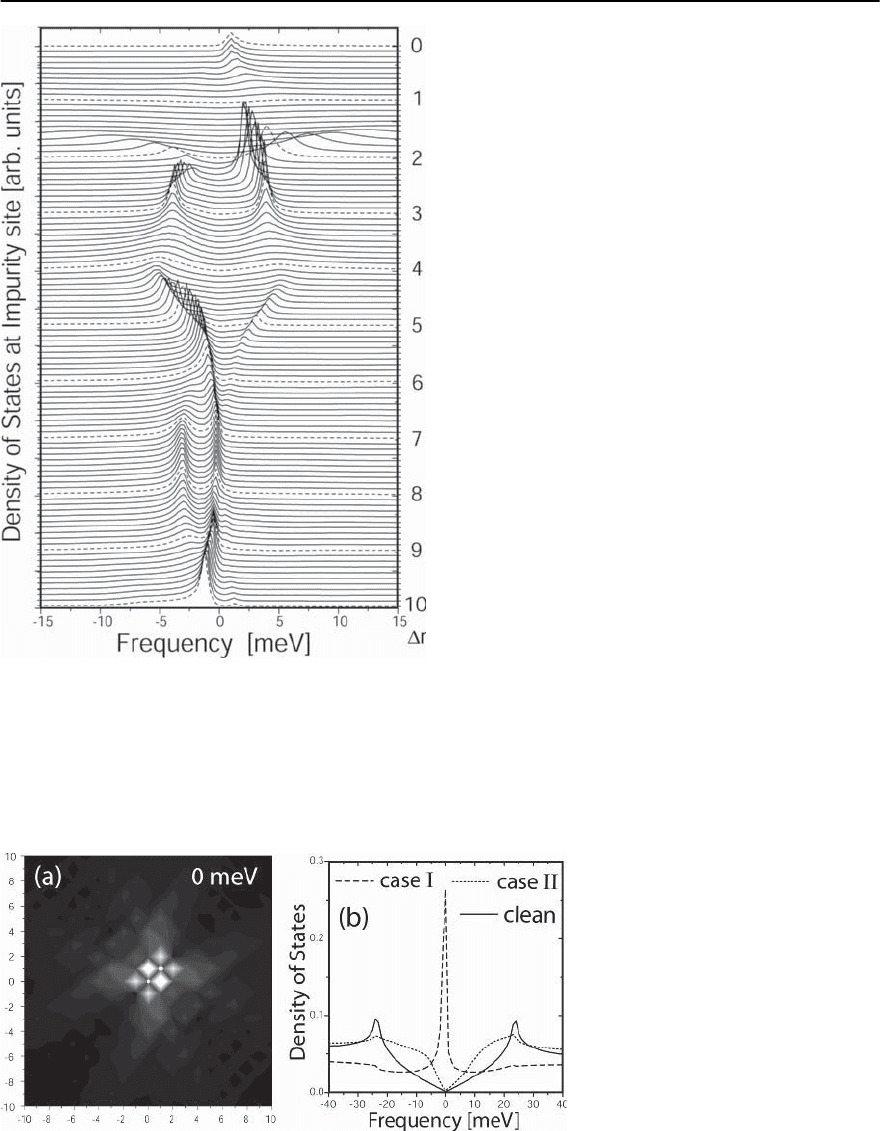
=(r, 0). In Fig. 6.13,

we present the LDOS at the impurity sites r

1,2

,asa

function of r [33]. For comparison, we note that

for a single impurity with U

= 700 meV, the reso-

nances are located §

res

= ±1.5meV.Astheinterim-

purity distance r is varied, the number of observ-

able low-energy resonances changes, the frequency

of the resonances oscillates and at the same time,

the width of these resonances in energy, which is a

measure of the resonance’s inverse lifetime, changes.

For example, for r ≤ 6, only two sharp low-energy

resonances can be clearly identified. Moreover, for a

single impurity, the resonance frequency and width

are correlated, such that as |§

res

| decreases, the fre-

quency width decreases as well [9,12]. In the case of

two impurities, we find that |§

res

| and the lifetime

of the resonances are not necessarily correlated. For

example, the resonance frequency for r =2.0and

r =3.5is§

res

= ±4.0 meV, but the width of the res-

onances are considerably larger in the second case.

Moreover, for some values of r, all resonances are

very weak and, for example, for r ≈ 1 disappear

almost completely. Note, that even for a rather large

interimpurity distance of r ≈ 10, the LDOS is still

affected by quantum interference.

Fig. 6.14. (a) Spatial plot of the LDOS

at §

res

=0meVfortwonon-magnetic

impurities located at r

=(0, 0) and

=(1, 1). Non-magnetic impurities

are represented by filled yellow circles.

(b) LDOS as a function of frequency at

(1, 0). Results are obtained within the

T-matrix formalism

246 D.K.Morr

The relative orientation of the two non-magnetic

impurities (the impurity dimer) with respect to the

underlying lattice possesses a strong effect on quan-

tum interference and the LDOS,and in particular,on

the mere existence of an impuritystate.If the two im-

purities are located at r

=(0, 0) and r

=(1, 1), and

thus are aligned along the (110)-direction (case I), a

resonancestateexistsat §

res

= 0 meV withthespatial

structure of the LDOS shown in Fig. 6.14(a). In con-

trast, if the impurities are located at r

=(0, 0) and



=(0, 1) (case II) and the dimer is aligned along the

(100)-direction, the LDOS exhibits only Friedel-like

oscillations,but no impurity resonance [33,37]. Sim-

ilar results were also obtained in Refs. [34–36]. This

striking difference is particularly apparent when one

plots the LDOS at (1, 0) as shown in Fig.6.14(b).This

dependence of the resonance on the dimer’s orien-

tation is similar to that of the zero bias conductance

peak (ZBCP) observed near one-dimensional surface

edges in the cuprate superconductors [94]. Only if

the electrons that are specularly scattered along the

impurity dimer experience a sign change in the su-

perconducting order parameter (and hence pairing

potential), a ZBCP-like impurity resonance emerges,

such as the one shown in Fig. 6.14(a) for case I. This

orientational dependence is an important feature of

nanostructures, as further discussed below.

How does the ZBCP-like state evolve when the

length of the impurity line along the (110)-direction

is increased? In Fig. 6.15(a) we show a spatial plot

of the LDOS for a line of N = 10 impurities that

are aligned along the (110)-direction. A character-

istic signature of the ZBCP-like state is that it ex-

tends spatially perpendicular to the impurity line.

Due to the hybridization of the ZBCP-like states on

both sides of the impurity line,and the resulting for-

mation of bonding and antibonding resonances, we

find that the ZBCP-like state is shifted away from

zero energy to §

res

= ±2 meV. The hybridization

is mediated by the next-nearest neighbor hopping

term (the t



-term), which permits the exchange of

electrons between the two sides of the impurity line

without a scattering process. When this hybridiza-

tion is suppressed, as for example, in the nanos-

tructure shown in Fig. 6.15(b), the ZBCP-like state is

again located at zero-energy. In this nanostructure,

the ZBCP-like states are spatially separated and the

absence of an impurity state between the two lines

prevents the coupling of the states and thus their

hybridization. A similar effect is also observed for

other nanostructures, such as squares (see below).

The same nanostructurealso induces impurity states

with other distinct spatial patterns,such as the“frog-

like” resonance shown in Fig. 6.15(c). Quite interest-

ingly, the global spatial pattern of this resonance ex-

tends along the (100)-direction,but consists of lines

with increased LDOS along the (110)-direction. As

the length of the impurity lines is further increased,

as in the nanostructure shown in Fig. 6.15(d) with

N = 68 impurities, the spatial extent of the ZBCP-

like state increases as well. Moreover, the spatial pat-

tern of the eigenmodes inside the nanostructure be-

comes more distinct, as shown in Figs. 6.15(e) and

(f). Note that the intensity of the ZBCP-like states

decreases algebraically as ∼ 1/r

along the (110)-

direction with distance from the nanostructure. For

the resonance at §

res

=0meVofasingleimpurity,

one has ˛ = 2 ( [10,25]). In contrast, we find ˛ < 2

up to distances, r, from the nanostructure that are

of order of its lateral size, l (note that for r  l,

one recovers ˛ = 2). For example, for the nanostruc-

ture shown in Fig. 6.15(b) with l =10

√

,wefind

˛ ≈ 1.18 up to a distance r ≈ 20a

perpendicular to

the lines. This decrease of ˛, which is expected since

for a truly one-dimensionalZBCPone has˛ =0,pro-

vides an explanation for the increasing spatial extent

of the ZBCP with increasing length of the impurity

line.

To further explore the interplay between geom-

etry and orientation, we next consider square-like

nanostructures,suchas the one shown in Fig.6.16(a)

whose sides are parallel to the (110)-direction [37].

This nanostructure induces a ZBCP-like resonance

at ! = 0 meV [Fig. 6.16(a)], which extends in all

four equivalent (110)-directions.The ZBCP-like res-

onances associated with each side are spatially sep-

arated and thus do not hybridize. Impurity states at

non-zero frequencies exhibit different characteristic

spatial patterns. The impurity resonance shown in

Fig.6.16(b) extends along the(100)-direction outside

the square with a“V-like”finestructure consisting of

branches that run along the (110)-direction.In con-