Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

4 Coexistence of Singlet Superconductivity and Magnetic Order 177

In the RE ternary superconductors the case 

 > 1

is realized and in this case

is given by

= 



S



+ QE

−

N(0)







e





−







1−

3





(4.39)

Here, N(0) is the electronic density of states per

electron spin and per magnetic atom. Based on the

free-energy in Eq. (4.39) we can study the coexis-

tence problem in the whole temperature region and

for various Ql; for more details see [34]. We sum-

marize the main results. (a)AtT = T

the sinu-

soidal magnetic order appears with the wave vec-

tor Q

∼ (1/a



)

1/3

where Q

is perpendicular

to S, i.e. the structure is transverse. (b)Bylowering

the temperature the striped domain structure ap-

pears with Q

∼ (1/a

)

1/2

, which is also transverse

and persists down to the temperature of the first or-

der phase transition T

where the DS phase passes

into the normal ferromagnetic state. At T

one has

, , Q

DS ,c2

, } = F

, 0, 0},whereQ

DS ,c2

≈

1.8(˜a(T

)

)

−1/2

∼ (a

)

−1/2

, (T

)=0.85

and

) ≈ 0.07(

); (c) The DS phase is sta-

ble down to T =0K if S

) > 1; this situa-

tion is realized in systems with small EX interaction

(which still dominatesover theEM one),i.e.for 



∼ (T

). (d)Indirty SC with (h)

 1there

is a gap in the quasiparticle spectrum for E <  in

the whole range of the domain phase existence. (e)

The calculations [8,10] show for clean SC in the DS

phase that the spectrum is gapless for h(T)   and

E  

N(E)

N(0)

h



4

, (4.40)

(f ) The spin-orbit interaction decreases the value of



n,0

−

s,0

(this also holds for small q) andthiseffectis

detrimental for the existence of the DS phase. How-

ever, the analysis in [38] shows that the spin-orbit

scattering can destroy the peak in 

s,q

in unrealisti-

cally dirty systems (l ∼ a)only.

We woul d l ike t o p oi nt o ut that a lo t o f stu dies

of ferromagnetic superconductors based on the phe-

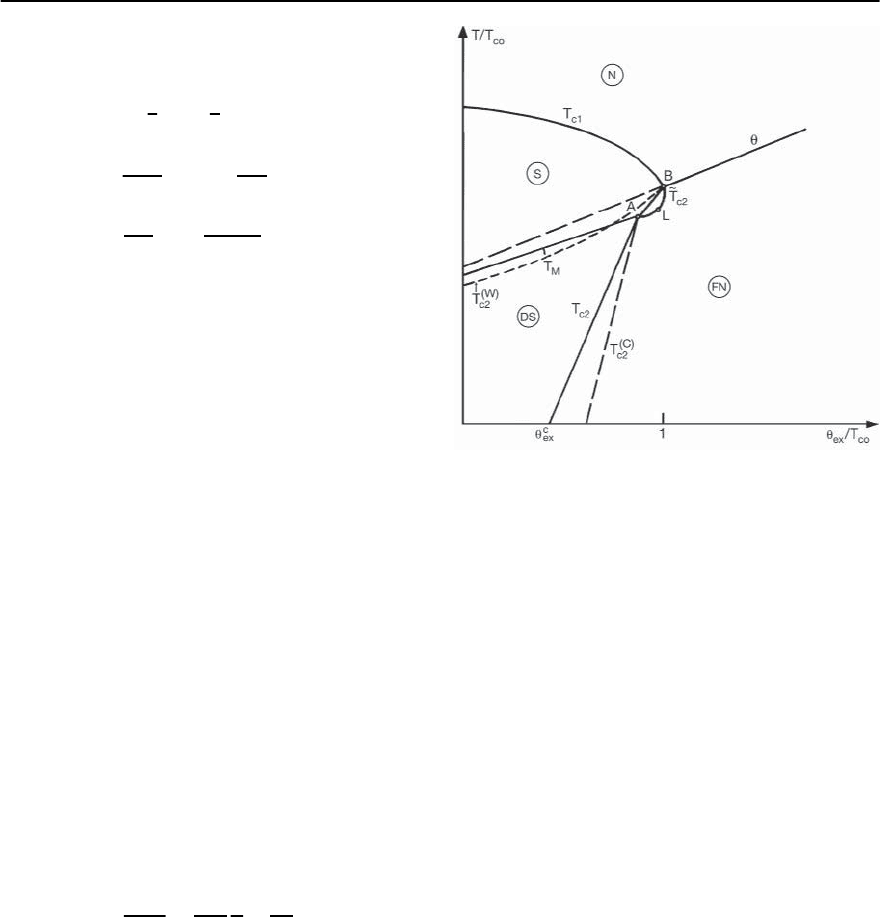
Fig. 4.8. Phase diagram of ferromagnetic superconductors

with easy plane anisotropy. Full lines separate N – para-

magnetic normal phase, S – superconducting phase, DS –

coexistence phase and FN ferromagnetic normal phases.

and T

are second order transition lines. Dash-dotted

line:  is the second order line that separates N and FN

phases in absence of the S phase. The dashed lines indi-

cate overheating and supercooling. T

is the first order

transition line from DS to ferromagnetic phase [8]

nomenological Ginzburg–Landau (G-L) theory take

into account the EM interaction only [33, 39]. Al-

thoughveryinteresting,thisphenomenology isinad-

equate in describing real materials,such as the above

cited RE ternary superconductors,where the EX in-

teraction prevails in the formation of the oscillatory

structure(with Q  

−1

, 

−1

) in the SC state.Finally,

based on the above theory the schematic phase di-

agram for RE ternary superconductors is calculated

and shown in Fig. 4.8.

Experimental Situation in the Coexistence Problem

The important microscopic parameters of the RE

ternary ferromagnetic superconductors with the co-

existence phase are extracted from various experi-

ments and are given in Table 4.1.

Based onthe proposedtheory and by using the mi-

croscopic parameters from Table 4.1 one concludes

178 M.L. Kuli´candA.I.Buzdin

Table 4.1. Basic parameters of some ferromagnetic super-

conductors. The parameters are defined in the text

ErRh

HoMo

n[cm

−3

] ∼ 10

∼ 4 × 10

[

]5.69.1

˜a[Å] ∼ 12.52.7



(0)[Å] 900 1200



[Å] 200 1500 470



[K]15.53.210

N(0)

−1

[K · spin] 1850 3600 1754

[cm · s

−1

]1.3 ×10

1.8 × 10



[K] 0.5–0.8 0.20.1 < 

[K]4024∼ 10



−1

[K]30.9



[K]1.81.3 ∼ 1.3

[K]8.71.85.5

[K] 0.8–1 0.7–0.74 0.53

[K]0.70.65 no

L =2 /Q[Å] 90–100 200 70–100

Fig. 4.9. Temperature dependence of the intensity of satel-

lite peaks and resistance in ErRh

single crystal [11]

that in ferromagnetic superconductors HoMo

ErRh

,HoMo

the superconductivity and os-

cillatory magnetic order coexist in a narrow temper-

ature interval. The unambiguous experimental evi-

dence of the existence of the non-uniform magnetic

structures was obtained from the neutron diffrac-

tion measurements in ErRh

[11], HoMo

[12]

and HoMo

[40]. For example, in Fig. 4.9 it is

demonstrated that in ErRh

[11] just below the

Curie temperature T

in the superconducting phase

the satellite neutron Bragg scattering appears in the

narrow temperature interval around (0.1–0.2) K be-

low the magnetic transition. Some peculiarities in

ErRh

, such as the appearance of the ferromag-

netic peak in the neutron scattering also in the coex-

istence phase (T

< T < T

), are explained by the

asperomagnetic ferromagnetic structure in the nor-

mal ferromagnetic state; see the extensive discussion

in [41]. The behavior of the first satellite in polycrys-

talline samples of HoMo

is well described by the

proposed theory, which also predicts that the inten-

sities of higher harmonics are very small and cannot

be seen experimentally [34].

Further lowering of the temperature provokes the

transition into the ferromagnetic state with the si-

multaneous destruction of the superconductivity,

which is in agreement with the theoretical predic-

tions.The period L of the oscillatory magnetic struc-

ture (either sinus or domain-like) in all three com-

pounds does not exceed the value L(= 2/Q) < 200

Å, i.e. 100 Å in HoMo

and 200 Å in ErRh

.This

important result means that the energetics of the co-

existence phase in the bulk sample is predominantly

due to the EX interaction, while, as we said above,

the EM interaction makes the structure transverse

(Q ·S = 0). The latter property is due to the fact that

in this case the density of “magnetic charges”is zero,

i.e. divM = 0, and the corresponding magnetic en-

ergy is also zero.In this sense the recent proposal [42]

of the coexistence of SC and the longitudinal (with

Q · S = 0) modulated (by SC) ferromagnetic order

should be abandoned, since the energy of this struc-

ture is higher than that of the transversal one. It can

be seen fromTable 4.1 that the compound HoMo

is different from the other two, since in it SC and the

oscillatory magnetic order coexist down to T =0.

4 Coexistence of Singlet Superconductivity and Magnetic Order 179

4.2.4 Domain Magnetic Structure in Thin

Supercondu cting Films

In the above calculations we have assumed that the

thickness L of the sample is very large, i.e. L 



, Q

−1

, so that the dissipated magnetic dipole en-

ergy (stray field) is negligible.In the case ofthin films

with L ∼ 

the stray magnetic energy E

,whichex-

ists around the domain walls and near the surface of

the sample, must be added to the free-energy F

Eq. (4.39). The total free-energy F

tot

= F

+ E

given by [43]

tot

/n =(

/n)+E

/n)+0.85

(T)

(4.41)

Inthecasewhenr(= F

(EM)

Int

(EX)

Int

)  1 the mini-

mization of F

tot

w.r.t. Q gives

tot

= Q

+ Q

. (4.42)

is the wave vector of the DS phase without the

stray magnetic energy and Q

≈ 1.6(

/ ˜aL)

1/2

the wave vector of the striped domain structure in

the normal ferromagnetic state. From Eq. (4.42) it is

seen that in a thin film of the ferromagnetic super-

conductor the period of the DS phase (d =2/Q

tot

)

is decreased due to the stray field. The theory based

on Eqs. (4.39) and (4.41) gives that the transition

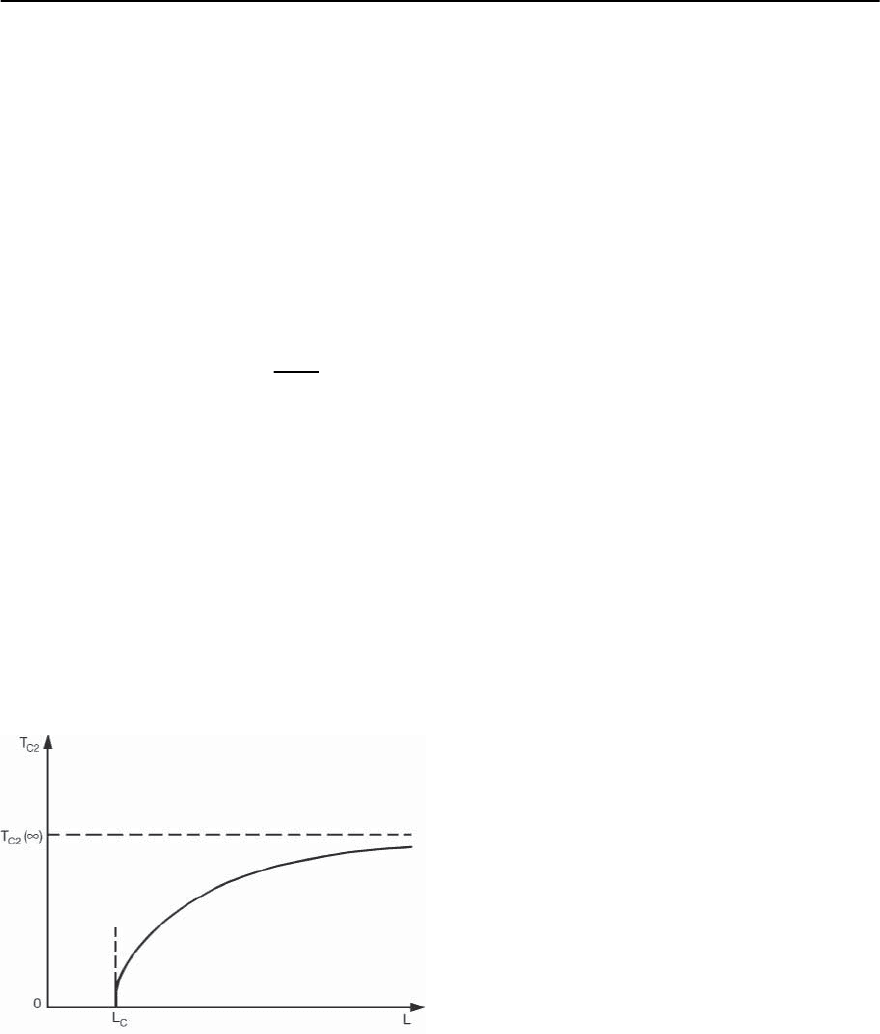
Fig. 4.10. Qualitative behavior of the DS-FN transition tem-

perature T

on the film thickness L of ferromagnetic

superconductor. For L = L

one has T

)=0and

(dT

/dL)

= ∞[43]

temperature T

(for the first order phase transition

DS → FN (with domains) can be pushed to zero

when L < L

=3

(

(L = ∞))/

(1 − S

(L = ∞))

; see Fig. 4.10. For the parameters from

Table 4.1 one obtains L

< 10

in HoMo

and

< 2

in ErRh

Some experiments in thin films of HoMo

show

such a thickness dependence of T

,whereT

(L) <

(∞) holds.Let us mention that even in the normal

ferromagnetic state, which is realized for T < T

there is a possibility that SC exists in domain walls

as it was shown in [44,45] and in more detailed cal-

culations in [8,46]. It seems that this situation is re-

alized in some pseudoternary compounds in which

 

4.2.5 Coexistence of Nuclear Magnetism

and Superconductivity

In 1997 Pobell’s group from Bayreuth made an im-

portant discovery [14] by observing that supercon-

ductivity and nuclear magnetism coexist in AuIn

which is type-I superconductor with T

=0.207 K

and T

=35 K. At first glance this is not too sur-

prising, having in mind the smallness of the hyper-

fine interaction between conduction electrons and

nuclear spins. However, the above exposed theory

of ferromagnetic superconductorsis very well appli-

cable also to this problem [15]. A surprising result

was obtained: the effective nuclear “exchange” field

(in fact, the hyperfine contact interaction) is rather

large h

hyp

≈ (0.6−1)K.Atthesametimethesu-

perconducting gap is 

≈ 0.4K,i.e.h

hyp

 

.We

point out that the hyperfine interaction has the same

(mathematical) structure as the exchange interaction

between the 4f LMs and conduction electrons

hyp





hyp

ı(r −R

) ˆ

†

(r)

ˆ (r) . (4.43)

Here, A

hyp

is the hyperfine interaction and the “hy-

perfine exchange field” is given by h

hyp

= nA

hyp



,

where

is the nuclear spin. It turns out that

the nuclear magnetism in AuIn

,whichshowsa

strong tendency toward the ferromagnetism in ab-

sence of SC, competes rather strongly with SC.

The estimation from the experiment [14] gives

180 M.L. Kuli´candA.I.Buzdin



(= 2n



)≈1 Kand

(≈N(0)h

hyp

)≈35 K,



≈10

Å,

≈10

Å,l≈3.6×10

Å(l < 

).This set

of parameters implies that the “EX” (hyperfine con-

tact) interaction is much stronger than EM (dipole–

dipole). The theory, which was originally invented

for the RE ternary compounds [8], is also applicable

to this problem. It predicts that if the nuclear mag-

netic anisotropy (which is due to the dipole–dipole

interaction) is small, i.e. (D/

) < 10

−3

,thespiral

magnetic structure should be realized. In the oppo-

site case (D/

)> 10

−3

the striped domain structure

is preferable. The experiments in magnetic field [14]

give indirect evidence that SC and a modulated mag-

netic order coexist up to T = 0 K.This case resembles

HoMo

,since in both cases the condition

< 

for T

= 0 is realized. Unfortunately, to date there

were no nuclear scattering measurements on AuIn

that can precisely resolve the nuclear magnetic struc-

ture below T

=35 K. We stress that the subject

of the coexistence of SC and nuclear magnetic or-

der is of enormous importance also for fundamen-

tal physics. These systems provide an opportunity

to study the coexistence problem in cases when the

electronic temperature (T

) is different from the nu-

clear one (T

), i.e. T

= T

. However, probably the

most interesting problem is the coexistence of SC

and nuclear magnetism for negative nuclear tem-

peratures (T

< 0 K). Unfortunately, the well-known

low-temperature Bayreuth laboratory closed several

years ago and further progress in this fascinating

field has stopped.

4.3 Antiferromagnetic Superconductors (AFS)

Most RE ternary borides and borocarbides show the

coexistence of superconductivity and antiferromag-

netic order (AF). In most of them the antiferromag-

netic N´eel temperature T

is smaller than T

,ascan

be seen from Table 4.2. In all of these superconduc-

tors the RE earth ions have localized 4f electrons (re-

sponsible for localized magnetic moments) that in-

teract with conduction electrons via the direct (local)

exchange interaction J

< 10

K.This fact makes the

theoretical analysis of their coexistence much easier

than in the case of theAF order in itinerant magnets.

Table 4.2. Superconducting and antiferromagnetic critical

temperature T

and T

, respectively, of various antiferro-

magnetic superconductors

(K) T

(K)

NdRh

5.31.31

SmRh

2.70.87

GdMo

1.40.84

TbMo

2.05 1.05

DyMo

2.05 0.4

ErMo

2.20.2

GdMo

5.60.75

ErMo

6.01.1

DyNi

C6.211

ErNi

C10.56.8

TmNi

C11 1.5

HoNi

C8 1.3

HoNi

C8.75

An evident experimental fact in RE ternary com-

poundsis that SC coexists withthe antiferromagnetic

(AF) order much more easily than with the modi-

fied ferromagnetic order. The reason for their weak

competitionlies in the fact that in the AF phase mag-

netic moments change their directions rapidly over

the atomic distances. Therefore, superconductivity

inﬂuences the AF order very weakly and the spin

susceptibility at the AF wave vector Q

(∼ a

−1

)is

practically the same as in the normal state



)−

)



(0)

≈



∼

 1 . (4.44)

This implies that in the free-energy F

(EX)

Int

their inter-

action part is very small and SC inﬂuences AF order

very weakly. However, the AF order affects SC more

strongly mainly via two basic effects. (a)Thespin

splitting ofelectronic levels by the exchange field and

producingpartial gapping of the Fermi surfacein the

normal state. This causes a decrease in the density of

states. In the SC phase the AF order can make SC

gapless on the part of the Fermi surface [47–49]. (b)

The magnetic scattering of conduction electrons on

spin ﬂuctuations above the N´eel temperature T

and

4 Coexistence of Singlet Superconductivity and Magnetic Order 181

on spin waves below T

is pair-breaking for Cooper

pairs [50].

(a) Let us brieﬂy analyze the AF superconductor in

the clean limit with the mean-field Hamiltonian

AFS



k,





†

k,

,

+  h

†

k+Q,

k,



+ 



k,+

−k,−

+ c .c)+



(4.45)

where Q is the AF wave vector and the SC order pa-

rameter is  = g



< c

k,+

−k,−

>, g > 0. The spin

projection is  = ±and h

is the Fourier component

of the AF exchange field. With a good accuracy one

has  ≈ const. since the theory shows [8,49] that its

spatialchangeissmall,i.e.ı(r)/ ∼ (h

Q)  1.

This means that in the RE ternary AF superconduc-

tors the pairing effects with non-zero momentum is

negligible. That is the reason that the results based

on the uniform pairing (with (r)=) [51] and

those in [47,48], where the non-uniform pairing is

also included,are practically the same [8,49]. By tak-

ing into account that   h

 v

AFS

can be

approximately diagonalized

AFS

≈



n,k

†

n,k

+small, (4.46)

where the spectrum E

n,k

is given by Eq. (4.36). The

term “small” accounts interband pairings, which are

negligible in the considered systems. As it is seen

the superconducting gap in the AF state is 

g,k

ı



+ h

.Itturnsoutthattheexactresultsob-

tained in [10] for the spiral order, given in II.A,re-

duce to those in Eq. (4.46) for   h

 v

Q.This

is understandable since the AF order is in many re-

spects similar to the spiral order with large Q.Inthat

case F

int

≈ 

(Q

)

−1

∼ (a/

)

which allows a

peaceful coexistence of SC and AF. By knowing the

spectrum E

n,k

it is easy to calculate thermodynamic

and other properties of clean AF superconductors.

For instance, in the case when T

< T

the critical

temperature is given by

≈ 1.14!

−1/



 =



k,n=1,2

ı(

n,k

− E

)

+ h

(4.47)

It is seen that the AF exchange field affects T

changing the density of states and by modulating the

electron wave functions ∼ ı

. The effect of h

the SC order parameter in clean systems is given by

ı/

≈ (h

Q)ln(h

/

)  1. In dirty systems

one obtains ı/

≈ T

 1sinceT

 T



 v

Q and 

 h

.These results are confirmed

in a number of the RE ternary compounds in which

the Ne´el temperature T

(≈ N(0)h

)isinmostcases

(much) smaller than T

[6].Due to the fast oscillation

of the magnetization in the AF state the EM interac-

tion is in general very small in AFS since the change

of K(Q)duetoAF is very small, i.e. ıK

(Q) ∼ a

(



)  1andalsoF

(EM)

Int

( F

(EX)

Int

). In clean sys-

tems with h

  there is a gapless line on the

Fermi surface, which gives the liner density of states

N(E)=N(0)(h

Q)E and the quadratic elec-

tronic specific heat C

(T)= (h

Q)T

[10,49].

Because the pre-factor (∼ h

Q)isverysmallin

AFS, the gapless effects are small in these systems.

(b)Themagnetic scattering, although pair-breaking,

is not very harmful for SC in real AF ternary com-

pounds, since the inverse life time 

−1

is small, i.e.



−1

∼ T

 T

. However, the effect of the mag-

netic scattering on the upper critical field H

may

be much more pronounced, especially at tempera-

tures near T

.Inthecasewhen

−1

∼ T

 T

which is, for instance, realized in TmRh

,theH

curve is weakly affected by the magnetic (exchange)

scattering. In cases where 

−1

∼ T

, for instance in

SmRh

, this scattering changes H

significantly;

see more in IV.B and [7,48,49].

Concerning the role of the non-magnetic scatter-

ing, already the above analysis on the decrease of 

tells us that non-magnetic impurities (characterized

by the life-time ) increase the depairing effect of

the exchange field, which means a breakdown of the

Anderson theorem [48,52]. In cases when T

 T

the effect of non-magnetic impurities is like that of

magnetic ones with the inverse scattering time



−1

h



1+(h

)

. (4.48)

When h

  1 one obtains 

−1

∼ T

≈ N(0)h

 T

, since (1/v

Q) ≈ N(0). This means that in

182 M.L. Kuli´candA.I.Buzdin

this case the pair-breaking effect of impurities is

rather small [52]. A very interesting situation is

realized in systems with T

 T

.Eveninsuch

a case the exchange field does not suppress T

significantly, since the theory [8, 49] predicts that

(ıT

) ∼ (h/E

)(ln h/E

)  1. However, in the

presence of non-magnetic impurities T

is renormal-

ized appreciably and SC disappears for the mean-

free path l < l

≈ 10

(h/v

) ∼ 

/h.Inthat

respect there is one very interesting AF supercon-

ductor Tb

with T

=19KandT

=0.8K.

In this case one expects (naively) that SC should dis-

appear due to the strong magnetic scattering. How-

ever, it turns out that in this compound the magnetic

anisotropy,in conjunctionwith the large momentum

J = 9, strongly suppress this pair-breaking effect,

thus giving rise to superconductivity.

4.3.1 Weak Ferromagnetism in Antiferromagnetic

Superconductors

In the case of the competition of SC and the fer-

romagnetic order in the RE ternary compounds the

theory predicts that in the presence of an appreciable

EX interaction SC can coexist only with spiral and

DS (or sinus) order, depending on the strength of

the magnetic anisotropy D. The realization of other

phases are improbable. It turns out that in AF su-

perconductors with weak ferromagnetism ( WF),of

Fig. 4.11.Phasediagram of weakFS in the T, ˇ plane.FS:the

Meissner phase with weak ferromagnetism; VS:thespon-

taneous vortex phase; DS: superconducting phase with do-

main magnetic structure [53]

the Moriya–Dyalozhinski type, the phase diagram is

much richer than in the case of ferromagnetic super-

conductors. For instance, the Meissner phase (M =0,

B =0)andthespontaneous vortex state [53] can be

realized in these systems; see Fig. 4.11.

Wediscussthisproblembrieﬂybystudyingthe

simplest AF order with two sublattices, in which case

l = S

− S

is the AF order parameter. In systems

that allow WF there is an additional term in the free-

energy F

= D[S

× S

], which is responsible for

the spin canting. If, for instance, l is along the xy-

plane and D is so oriented that it allows the appear-

ance of the weak ferromagnetism, then m = S

+ S

(M = nm)alsoliesinthexy-plane but l ⊥ m.In

this case F

is given by

= ˇn 

+ m

) . (4.49)

Since in most systems m ∼ 10

−3

l, this immediately

implies that the parameter ˇ  1. In this case and

when T

 T

the interaction part F

int

of the total

free-energy (F = F

int

) is given by Eq.(4.14),

while the magnetic system is described by F



r



)

+ bm

+ a

(∇l)







ˇ

+ m

(B −4M)

8



(4.50)

The minimization of F with respect to A, l, m

and q gives an very rich phase diagram for AFS

with WF [8,49,53].We stress that the resulting free-

energy F is similar to the case of ferromagnetic su-

perconductors in Eq. (4.15) with an effective mag-

netic stiffness a

eff

=(ab/ˇ)  a.Itturnsoutthat

if ˇ  a/

, the EX interaction dominates in the

formation of the magnetic structure, and the sinus

structure (l ∼ sin Qr and m ∼ sin Qr)isrealized

at and below T

, while for (a/

) < ˇ  a/

the

EM interaction prevails in the formation of the si-

nusoidal structure. If ˇ < (a/

)

√

2

/

,then

the non-uniform structure is unfavorable and the

so-called Meissner state (first proposed by Vitalii

Ginzburg in 1956) is realized. It is characterized by

M = const. and by the averaged (over the sample

cross-section) magnetic induction < B > =0inthe

bulk sample (Notethat B =4M exp{−z/

}),which

4 Coexistence of Singlet Superconductivity and Magnetic Order 183

is due to the SC screening current on the surface of

the sample. By further lowering the temperature the

sublattice magnetization | S

1,2

| grows and it is nec-

essary to take into account higher order terms in

F. As a result one obtains that for ˇ 



a/

the

EX interaction dominates again and the striped DS

phase is realized, while for



a/

 ˇ 



a/

the striped DS phase is realized due to the EM in-

teraction. However, by lowering the temperature the

domain wall energy grows and it my happen that

a spontaneous vortex state,with4M > H

,the

lower critical field, is realized for ˇ 



a/

and

for the AF vector l > l

∼ (H

/M(0))(ˇ

/˜a

)

1/3

˜a = a[(T

−T)/T

]

1/2

,see Fig.4.11.Fromthe known

RE ternary compounds a good candidate for such a

behavior is the body centered tetragonal (b.c.t.) sys-

tem ErRh

4.4 Magnetic Superconductors

in the Magnetic Field

4.4.1 Ferromagnetic Superconductors

There are a number of interesting effects of the

magnetic field H either in the coexistence phase or

above the magnetic transition temperature T

where

S(T > T

)=0.Wediscusssomeofthembrieﬂyand

for more details see [8,38].

DS Phase in the Magnetic Field

It is known that in the bulk sample the applied mag-

netic field penetrates only on the length 

,thusaf-

fecting the surface of the sample only. However, in

thin films the paramagnetic effectof the field is more

important than the orbital one [8]. This problem was

studied in the case of a thin (along the y-axis) film

with the thickness L

< 

, when the magnetic field

is para llel to the striped domains, i.e. H = He

.Asa

result the magnetization S

(x) contains, besides the

odd harmonics, also the zeroth-one as well as the

even harmonics

(x)=

Sı +

∞



k=1

k



[1 − (−1)

cos(kı)] sin(kQx)

+(−1)

sin(kı)cos(kQx)



, (4.51)

with ı = H/2S

. This change of harmonics in

(x) can be observed in magnetic neutron diffrac-

tion experiments. Equation (4.51) tells us that do-

mains with M parallel to H increase their thickness,

i.e. d → d(1 + ı), while the thickness of antiparal-

lel domains is decreased, i.e. d → d(1 − ı). In the

case when the zeroth component of the exchange

field is sufficiently large, i.e. when

h(= h

Sı) >

[1 − (1/

)

2/3

]

2/3

the DS phase is destroyed by

the Zeeman effect and SC disappears, i.e.  =0.

For

h <

the parameters of the DS phase are

renormalized, for instance one has Q(H) < Q(0).

InthecasewhenH = He

(i.e. the field is orthogo-

nal to the z-axis), all domains have the same thick-

ness and there is no redistribution of intensities of

neutron peaks. However, there is only a decrease of

intensities of (2k +1)Q peaks by the factor (1 − ı

⊥

)

where ı

⊥

= H/S(

+ D

)andD

is the magnetic

anisotropy.

FS in magnetic ﬁeld at T > T

The effect of the exchange field on SC in magnetic

field is negligible for T  T

, since for T

 T

the magnetic susceptibility

is very small near T

However, at T near T

there is a pronounced increase

of 

and accordingly an increase of the paramag-

netic effect. This means that at temperatures T ∼ T

the applied field strongly affects the superconductiv-

ity.

(i) Thermodynamic critical field H

(T). We illustrate

this effect by analyzing the change of the thermo-

dynamical field H

(T) (for the transition N → MS)

in magnetic superconductors. In this case the Gibbs

energy density of the paramagnetic normal phase

is equal to that of the SC phase,

)

where

(0) −

8

, (4.52)

)=F

(0) −

H

8

. (4.53)

This gives the critical field

(T)=

(T)



1+4

(T)

, (4.54)

184 M.L. Kuli´candA.I.Buzdin

where (H

/8)=N(0)

/2 is the SC condensa-

tion energy and the magnetic permeability is  =

1+4

. (Note that we neglect the conduction elec-

tron susceptibility

since in MS one has 

 

In ferromagnetic superconductors for T > T

one

has 

(T) ≈ (

/4)/(T − T

)and

(T) ∼



T − T

. (4.55)

It is seen from Eq. (4.55) that H

(T) is drastically re-

duced near T

 T

, due to divergence of 

(T).

Very near T

non-linear effects of the magnetic field

start to dominate.

(ii) Upper critical field H

(T). In the presence of

the external field H

and at temperatures near and

above T

the superconductivity is suppressed by

the orbital effect of the field B = H

(1 + 4

)

and by the pronounced paramagnetic effect of the

exchange field h (since the Zeeman effect of B is

much smaller). Here, the internal magnetic field is

= H

where H

is the demagnetization field.

The upper critical field is calculated by the same for-

mula as for non-magnetic SC, see [54], where 

replaced by ˜

= 

+ h

M/nH

and the electron

charge e by ˜e = e(1+4M/H

).In the clean limit,and

for T  T

, one obtains the modified Gruenberg–

G¨unther formula for H

(T) [55]

(T)=

√

1+4

(T)

∗

(0)

f (˛)

, (4.56)

where H

∗

(0) us the upper orbital critical field in ab-

sence of magnetic moments. The function f (˛)is

calculated numerically in [55] and the parameter ˛

describes the relative role of the orbital and param-

agnetic effect

˛ =

∗

(0)h



(T)

(1 + 4

(T))n

. (4.57)

In the RE ternary magnetic superconductors one

usually has h

 

and 4M =4n,whichis

oneorderofmagnitudesmallerthanH

∗

(0). This

gives ˛  1 in the region where T  T

.Itis

known that in puresuperconductorsfor˛ > 1.8 [55]

the Larkin–Ovchinikov–Fulde–Ferrell (LOFF) phase

(due to paramagnetic effects) is realized [56,57]. In

the LOFF state the SC order parameter oscillates spa-

tially, also being zero at some points. For ˛  1one

has f (˛) ≈ 1and

(T) ≈ 1.5





(T − T

) . (4.58)

It is seen that H

(T) depends linearly on T − T

near T

and falls off much faster than H

(T)by

reaching the value H

< H

near T

.Thisleadstoa

very interesting effect: at H

(T) the system goes into

the Meissner or vortex state by the first order phase

transition,depending on the relation between H

and

. Various phases can be realized in the H − T

phase diagram depending on the demagnetization

factors and sample purity as is shown in Fig. 4.12.

For instance, the theory predicts the existence of

the Larkin–Ovchinikov–Fulde–Ferrell (LOFF) state

in clean samples (l > 

) with finite demagnetiza-

tion factorsas shown in Fig. 4.12a,c.

Fig. 4.12. (H, T) phase diagram for

ErRh

above T

with demagneti-

zation factors: (a) N

=1/3, (b) N

0, (c) N

=1.H is along the a-

axis. MS: Meissner phase, VS:vortex

phase, LOFF: Larkin–Ovchinikov–

Fulde–Ferrel phase [8]

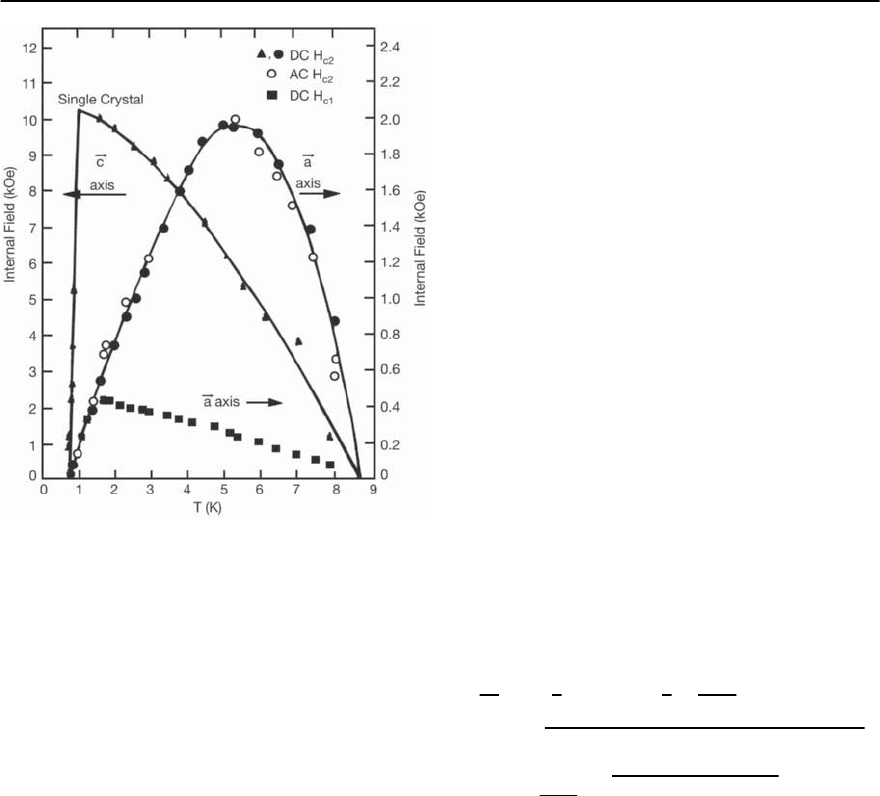
4 Coexistence of Singlet Superconductivity and Magnetic Order 185

Fig. 4.13. Experimental upper critical field H

vs.tempera-

ture for c-axis and a-axis directions in ErRh

.Thelower

critical field H

along the a-axisisalsoshown;thatforthe

c-axis is similar [58]

The magnetization and H

measurements in

ErRh

[58] give that the samples were clean and

that the experimental curve, shown in Fig. 4.13, re-

sembles strongly the theoretical ones in Fig. 4.12.The

conclusion is that the behavior ofthe critical fieldH

in ErRh

uniquely proves the dominant role of the

EX mechanism inthe destructionof superconductiv-

ity near the magnetic transition temperature T

(iii) H

in polycrystalline FS.Most ferromagnetic su-

perconductors were synthesized as polycrystals and

are also characterized by the rather large anisotropy

of the magnetic susceptibility near T

,i.e.M



. For instance in ErRh

with the easy plane

anisotropy one has 

/

⊥

≈ 1/64. Sincethe effective

exchange field is large in these compounds it inﬂu-

ences superconductivity strongly.

If the size of the crystallites is larger than the su-

perconducting coherence length 

,thenH

in each

crystallite depends critically on the direction of the

applied field H. If the orientations of the crystallites

are random, then the decrease of the magnetic field

increases the number of crystallites that are in the su-

perconducting state. This causes the decrease of the

sample resistance. When the concentration of crys-

tallites,where the superconductivity is set in,reaches

the critical concentration C

=0.25 in 3D systems, a

continuous superconducting path appears through-

out the sample.In this case the resistance of the sam-

ple is significantly decreased. Therefore, we are here

dealing with a typical percolation phenomenon in

ferromagnetic superconductors as it was recognized

and studied in [59].

In the field H

min

< H < H

max

the concentration

C(H) of crystallites in the superconducting state is

C(H) = 1 − cos

(H), where 

(H)isthebound-

ary angle between the applied field H and the axis

of anisotropy up to which superconductivity is pre-

served. This angle is determined from the condi-

tion that H = H

(

), i.e. the given H is the crit-

ical field for the angle 

.TocalculateH

(

)one

should take into account:(i) the exchange field which

acts on electronic spins, h

=  (

⊥

+ 



)

1/2

with  = J

−1)/n

and (ii) the orbital field

|B = H +4M |. Since the studied polycrystals

of ErRh

where in the dirty limit H

()isthen

given by

= (

)−Re





DeH

2T





(1 + 4

⊥

)

sin

 +(1+4



)

cos



+ i



2T





⊥

sin

 + 



cos





. (4.59)

was experimentally determined from the con-

dition R

)/R

=0.5, where R

is the measured

resistance and R

isthenormal resistance.The perco-

lation theory gives the relation between the effective

medium resistance R

and the concentration C(H)

of crystallite in the superconducting state by [61]

(H)=R

[1 − 3C(H)] . (4.60)

If one uses the experimental values for 

⊥

≈ 0.087

and 

⊥

≈ 64



and for the coefficient of diffusion D

obtained fromtheslope of H

at T

one obtains very

nice agreement for R

(H)atT =4.35 K between this

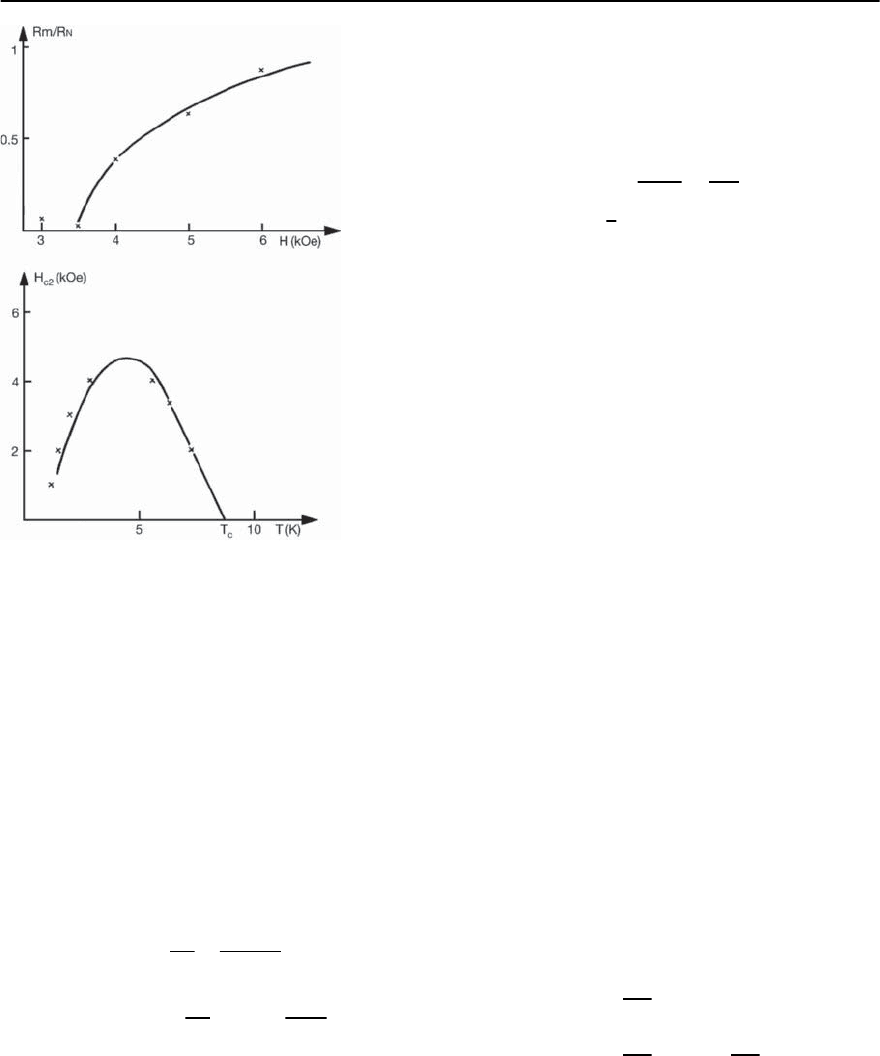
186 M.L. Kuli´candA.I.Buzdin

Fig. 4.14. Resistance R

(H) and upper critical field H

vs.

temperature of polycrystalline ErRh

. Line: theory [59];

(x): experimental results [60]

theory and experiments; see Fig. 4.14. In such a way

the determined experimental curve H

(T)isvery

well described by this theory [59] as can be seen in

Fig. 4.14.

(iv) Lower critical field. H

is very weakly affected

bytheexchangefield.Thiscanbeeasilydemon-

strated by adding to Eq. (4.10) the magnetic field

term −



B·HdV/4.The minimization of the Gibbs

free-energy with respect to the relative magnetiza-

tion S(r) one obtains the Gibbs-energy for the single

vortex

G =







8

32





∇' −

2



−

B · H

4



(4.61)

Here ' is the phase of the SC order parameter, ¥

the ﬂux quantum and p

=1−

(

+ 

+ ˜





(T))

−1

is the“screening”parameter that charac-

terizes the renormalization of the Meissner screen-

ing in the presence of the exchange field [8]. Here



(T)= ˜

/(T − T

) is the magnetic susceptibility.

By minimizing G in Eq. (4.61) with respect to A one

obtains H

in the standard way

4



eff



, (4.62)

where 

eff

= 

√

p. Note that in the theory, which

neglects the EX interaction, i.e. with 

=0,oneob-

tains p

→ 0 for T → T

.Thisoddresultmeans

that the effective penetration depth 

eff

tends to zero

and the Ginzburg–Landau (G-L) parameter also goes

to zero,i.e.  =(

eff

/) → 0.If this assumption were

realized in the RE ternary superconductors, then at

temperatures near T

we would have a change from

type-II to type-I superconductivity. However, this

cannot be realized in the RE ternary superconduc-

tors, since one has 

∼ 

,thusmakingp finite

andthe G-L parameter  stayspractically unchanged.

So, the change of the type of transition near T

not due to the change of  but to the much faster

temperature fall-off of H

(T)thanofH

(T)[8].

(v) Surface energy of fer romagnetic superconductors.

A very interesting result is obtained for the surface

energy 

(FS)

of ferromagnetic superconductors (FS)

placed in magnetic field at T > T

.Inthiscasein

the normal state the magnetization is M = 

H and

decays in FS on the distance 

eff

. The surface energy

of FS was calculated in [62] and it was obtained that

in systems with large Ginzburg–Landau parameter



eff

= 

eff

/ the surface energy 

(FS)

(T) changes sign

at some temperature T

> T

,as shown in Fig.4.15.

The reason for such a behavior lies in the strong tem-

perature dependence of the thermodynamic critical

field H

(T)(< H

(T)) given by Eqs. (4.54)–(4.55).

The surface energy for non-magnetic( 

(S)

)andfer-

romagnetic (

(FS)

) superconductors has the follow-

ing approximate forms, respectively ( = /)



(S)

= 

8

(1 − ) , (4.63)



(FS)

= 

8



1−

eff



. (4.64)

The first term in Eqs. (4.63) and (4.64) denotes the

lossin thecondensationenergy onthe length ,while