Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


3 Electron–Phonon Superconductivity 97
The spectral representation for the phonons is al-
ready present in Eqs. (3.43) and (3.45). Therefore
the Matsubara sum can be performed straightfor-
wardly (see, for example, [12,81]), and the analyti-
cal continuation can be done. Upon integrating over
momentum (using, as in Eqs. (3.55)–(3.58) electron-
hole symmetry and a constant (and infinite in extent)
density of electron states),one arrives at the standard
real-axis Eliashberg equations [4, 12]. These equa-
tions are much more difficult to solve than the imag-
inary axis counterparts.They require numerical inte-
gration of principal value integrals and square-root
singularities, and the various Green function com-
ponents are complex. In contrast the imaginary axis
equations are amenable to computers (the sums are
discrete) and the quantities involved are real. More-
over a considerable number of thermodynamic and
magnetic properties can be obtained directly from
the imaginary axis solutions.
The discrepancy in computational ease between
the two formulations led to an alternative path to
dynamical information, namely the direct analytic
continuation of the solutions of the imaginary axis
equations to the real axis by a fitting procedure with
Pad´e approximants [160]. This method is in general
very sensitive to the input data, and has (surmount-
able [161,162]) difficulties at high temperatures and
frequencies.
More recently yet another procedure was formu-
lated [163],which first requires a numerical solution
of the imaginary axis equations, followed by a nu-
merical solution of analytic continuation equations.
This latter set is formally exact (i.e. no fitting re-
quired) and yet avoids the complications of the real-
axis equations. These equations are
£(k, z)=
1
Nˇ
∞
k
m
=−∞
kk
(z − i!
m
)
N()
G(k
, i!
m
)
+
1
N
k
∞
0
d
˛
2
kk
F( )
N()
(3.75)
×
f ( − z)+N( )
G(k
, z − )
+
f ( + z)+N( )
G(k
, z + )
,
(k, z)=
1
Nˇ
∞
k
m
=−∞
kk
(z − i!
m
)
N()
− V
kk
× F(k
, i!
m
)
+
1
N
k
∞
0
d
˛
2
kk
F( )
N()
(3.76)
×
f ( − z)+N( )
F(k
, z − )
+
f ( + z)+N( )
F(k
, z + )
,
where z can actually be anywhere in the upper half-
plane. Thus, for example, Eqs. (3.43) and (3.45) can
be recovered by substituting z = i!
m
. On the other
hand, once these equations have been solved, one
can substitute z = ! + iı, and iterate the result-
ing equations to convergence. When the “standard”
approximations for the momentum dependence are
made (i.e. Fermi surface averaging, constant density
of states, particle-hole symmetry, etc.) the result is
Z(! + iı)=1+
iT
!
∞
m=−∞
(! − i!
m
)
×
!
m
Z(i!
m
)
!
2
m
Z
2
(i!
m
)+
2
(i!
m
)
(3.77)
+
i
!
∞
0
d˛
2
F( )
N( )+f ( − !)
×
(! − )Z(! − + iı)
(! − )
2
Z
2
(! − + iı)−
2
(! − + iı)
+
N( )+f ( + !)
×
×
(! + )Z(! + + iı)
(! + )
2
Z
2
(! + + iı)−
2
(! + + iı)
,
(! + iı)=
T
∞
m=−∞
(! − i!
m
)−
∗
(!
c
)(!
c
− |!
m
|)
×
(i!
m
)
!
2
m
Z
2
(i!
m
)+
2
(i!
m
)
(3.78)

98 F. Marsiglio and J.P. Carbotte
+ i
∞
0
d˛
2
F( )
N( )+f ( − !)
×
(! − + iı)
(! − )
2
Z
2
(! − + iı)−
2
(! − + iı)
+
N( )+f ( + !)
×
(! + + iı)
(! + )
2
Z
2
(! + + iı)−
2
(! + + iı)
.
Note that in cases where the square-root is complex,
the branch with positive imaginary part is to be cho-
sen.
One important point has been glossed over in
these derivations. Because of the infinite bandwidth
approximation, an unphysical divergence occurs in
the term involving the direct Coulomb repulsion,
V
k,k
, both in the imaginary axis formulation,(3.58),
and in the real-axis formulation, Eq. (3.78). The so-
lution to this difficulty is to introduce a cutoff in
frequency space (even though the original premise
was that the Coulomb repulsion was frequency in-
dependent), as is apparent in the two equations. In
fact, this cutoff should be of order the Fermi energy,
or bandwidth. However, this requires a summation
(or integration) out to huge frequency scales. In fact
one can use a scalingargument [3,164,165] toreplace
thissummation(or integration)byonewhich spansa
small multiple (≈ 6) of the phonon frequency range.
Hence the magnitude of the Coulomb repulsion is
scaled down, and becomes [164]
∗
(!
c
) ≈
N()U
1+N()U ln
F
!
c
, (3.79)
where U is a double Fermi surface average of the
direct Coulomb repulsion. This reduction is cor-
rect physically, in that the retardation due to the
phonons should reduce the effectiveness of the direct
Coulomb repulsion towards breaking up a Cooper
pair. It does appear to overestimate this reduction,
however [166].The analytic continuationof this part
of the equations has been treated in detail in [167].
In the zero temperature limit, Eqs. (3.77) and
(3.78) are particularly simple. Then the Bose func-
tion is identically zero and the Fermi function be-
comes a step function: f ( − !) → (! − ). Once
the imaginary axis equations have been solved, so-
lution of Eqs. (3.77) and (3.78) no longer requires
iteration. One can simply build up the solution by
construction from ! = 0 (assuming ˛
2
F( )hasno
weight at = 0); in fact, if the phonon spectrum has
no weight below a frequency,
min
, then only the first
lines in Eqs. (3.77) and (3.78) need be evaluated. In
particular, if the gap (still to be defined) happens to
occur below this minimum frequency (often a good
approximation for a conventional superconductor)
then the gap can be obtained in this manner.
1
In the following two sections we explore the pos-
sibilityof using Eqs.(3.77)and (3.78)to obtaininfor-
mation about the microscopic parameters of Eliash-
berg theory.
Tunneling
Perhaps the simplest, most direct probe of the exci-
tations of a solid is through single particle tunneling.
In this experiment electrons are injected into (or ex-
tracted from) a sample, as a function of bias voltage,
V.The resultingcurrent is proportional to the super-
conducting density of states [46,168–170]:
I
S
(V) ∝
d!Re
|!|
√
!
2
−
2
(!)
f (!)−f (! + V )
,
(3.80)
wherewehaveusedthegapfunction,(!), defined
as
(!) ≡ (! + iı)/Z(! + iı). (3.81)
The proportionality constant contains information
about the density of states in the electron supplier (or
acceptor), and the tunneling matrix element. These
are usually assumed to be constant. If one takes the
zero temperature limit,then the derivative of the cur-
rent with respect to the voltage is simply proportional
to the superconducting density of states,
dI
dV
S
/
dI
dV
N
=Re
|V|
V
2
−
2
(V)
%
, (3.82)
1
The reader may notice that this amounts to simply changing the imaginary frequency i!
m
where it occurs in Eqs.(3.55)
and (3.56) to ! before doing the Matsubara sum.
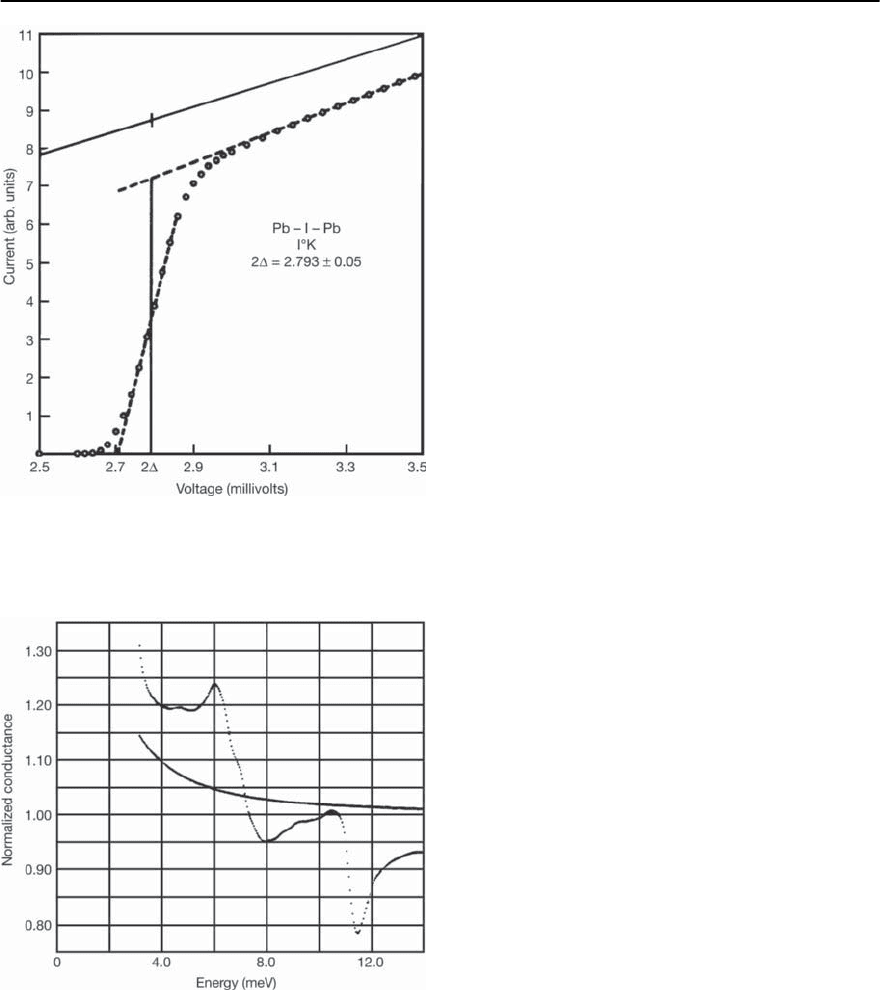
3 Electron–Phonon Superconductivity 99
Fig. 3.16. I-V characteristic of a Pb-I-Pb junction showing
the construction used to find the energy gap.The solid line
and open circles are the current in the normal and super-
conducting states, respectively. Reproduced from [50]
Fig. 3.17. Conductance dI/dV of a Pb-I-Pb junction in
the superconducting state normalized by the conductance
in the normal state vs. voltage. Also shown is the two-
superconductor conductance calculated from the BCS den-
sity of states which contains no phonon structure. Repro-
duced from [50]
where S and N denote “superconducting” and “nor-
mal” state, respectively. The right-hand side of
Eq. (3.82) is simply the density of states, computed
within the Eliashberg framework (see, for example,
[50]). It is not at all apparent what the structure of
the density of states is from Eq. (3.82), until one has
solved for the gap function from Eqs. (3.77), (3.78)
and (3.81). At zero temperature the gap function
(!) is real and roughly constant up to a frequency
roughly equal to that constant. This implies that the
density of states will have a gap, as in BCS theory.At
finite temperature the gap functionhas a small imag-
inary part starting from zero frequency (and, in fact
therealpartapproacheszeroatzerofrequency[171])
so that in principle there is no gap,even for an s-wave
order parameter. In practice, a very well-defined gap
still occurs for moderate coupling, and disappears at
finite temperature only when the coupling strength
is increased significantly [172,173].
In Figs. 3.16 and 3.17 we show the current-
voltage and conductance plots for superconducting
Pb, taken from McMillan and Rowell [50]. These
data were obtained from a superconductor-insulator-
superconductor (SIS) junction,with Pb being the su-
perconductor on both sides of the insulating barrier,
sothat,ratherthandirectlyusingEq.(3.82),thecur-
rent is given by a convolution of the two supercon-
ducting densities of states. Two features immediately
stand out in these plots.First, a gap is clearly present
in Fig. 3.16, given by 2
◦
,where
◦
is the single elec-
tron gap defined by
◦
≡ Re(! =
◦
), (3.83)
a definition one can use for all temperatures. Sec-
ondly, a significant amount of structure occurs be-
yond the gap region, as is illustrated in Fig. 3.17.
McMillan and Rowell were able to deconvolve
their measurement, to produce the single electron
density of states shown in Fig. 3.18. Since the su-
perconducting density of states is given by the right
hand side of Eq. (3.82), the structure in the data
must be a reflection of the structure present in the
gap function, (!). The structure in the gap func-
tion is in turn a reflection of the structure in the
input function, ˛
2
F( ). In other words, Eqs. (3.77)
and (3.78) can be viewed as a highly nonlinear
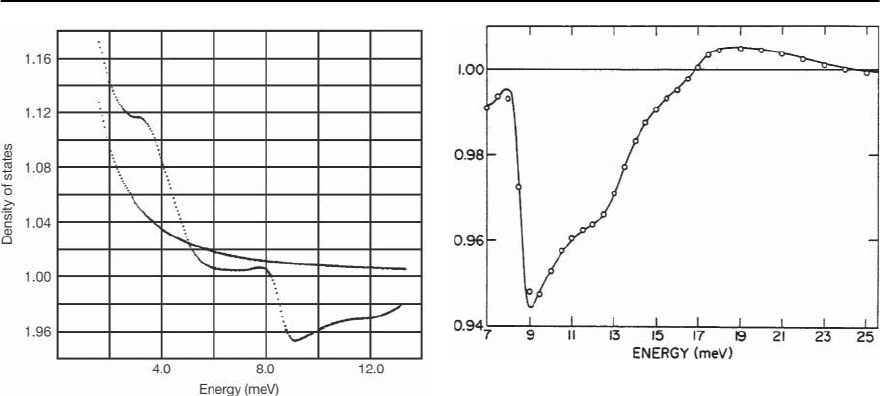
100 F. Marsiglio and J.P. Carbotte
Fig. 3.18. Electronic density of states N(E)vs.E −
◦
for Pb,
obtained from the data of Fig.3.17.The smoo th curve is the
BCS density of states. Reproduced from [50]
transform of ˛
2
F( ). Thus the structure present in
Fig. 3.18 contains important information (in coded
form) concerning the electron–phonon interaction.
One has only to“invert”the“transform”to determine
˛
2
F( ) from the tunneling data. This is precisely
what McMillan and Rowell [48, 50] accomplished,
firstinthecaseofPb.
The procedure to do this is as follows. First a
“guess”ismadefortheentirefunction,˛
2
F( ), and
the Coulomb pseudopotential parameter,
∗
.Then
the real axis Eliashberg equations (Eqs. (3.76 and
(3.77)) are solved, and the superconducting den-
sity of states (Eq. (3.82)) is calculated. The result
attained will in general differ from the experimen-
tally measured function (represented, for example,
by Fig. 3.18); a Newton–Raphson procedure (using
functional derivatives rather than normal deriva-
tives)isusedtodeterminethecorrection tothe initial
guess for ˛
2
F( ) that will lead to better agreement.
Very often another parameter (for example,the mea-
sured energy gap value) is used to fit
∗
.Thisprocess
is iterated until convergence is achieved. The result
for Pb is illustrated by the dotted curve in Fig. 3.13.
Once ˛
2
F( )(and
∗
) has been acquired in this
way one can use the Eliashberg equations to calculate
other properties, for example, T
c
. These can then be
compared to experiment, and the agreement in gen-
Fig. 3.19. The predicted (solid curve) normalized density of
states in Pb as a function of energy ! compared with mea-
sured values (open dots) as a function of energy measured
from the gap edge. The measured density of states divided
by the BCS density of states above 11 meV was not used
in the fitting procedure that produced ˛
2
F(!)andacom-
parison of theory and experiment in the multiple-phonon
region is a valid test of the theory. Reproduced from [50]
eral tends to be fairly good. One may suspect, how-
ever,a circular argument,since the theory was used to
produce the spectrum (from experiment), and now
the theory is used as a predictive tool, with the same
spectrum. There are a number of reasons, however,
for believing that this procedure has produced mean-
ingful information. First, the spectrum attained has
come out to be positive definite, as is required phys-
ically. Second, the spectrum is non-zero precisely in
the phonon region,asit shouldbe.Moreover,it agrees
very well with the calculated spectrum. Thirdly, as
already mentioned, various thermodynamic prop-
erties are calculated with this spectrum, with good
agreement with experiment. Finally, the density of
states itself can be calculated in a frequency regime
beyond the phonon region, as is shown in Fig. 3.19.
The agreement with experiment is spectacular.
None of these indicators of success can be taken
as definitive proof of the electron–phonon interac-
tion. For example, even the excellent agreement with
the density of states could be understood as a mathe-
matical property of analyticfunctions[174].Also,we
have focussed on Pb; in other superconductors this
procedure has not been so straightforward. For ex-
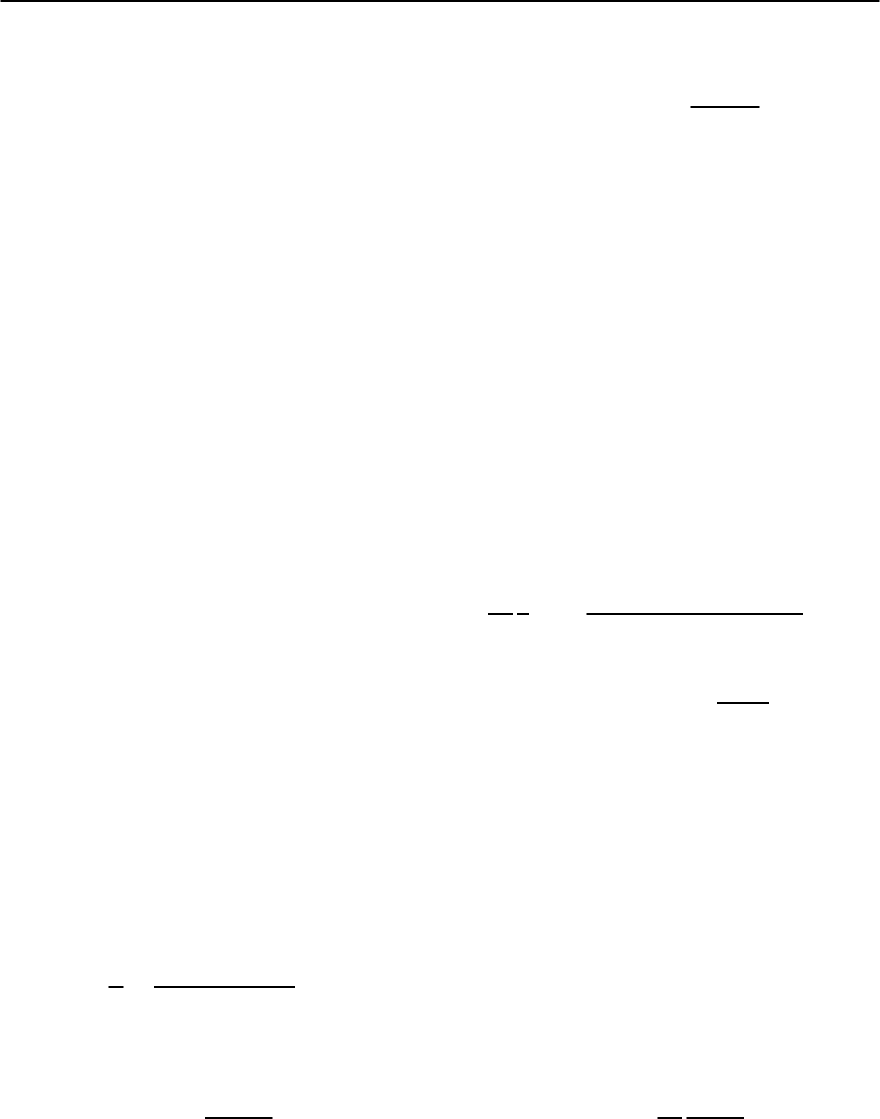
3 Electron–Phonon Superconductivity 101
ample,in Nb a proximity layer is explicitly accounted
for in the inversion [170,175], thus introducing ex-
tra parameters. In the so-called A15 compounds (eg.
Nb
3
Sn, V
3
Si,etc.),althoughthemeasuredtunnel-
ing results have been inverted [142], several experi-
ments do not fit the overall electron–phonon frame-
work [9].
More details are provided in [10]. An alternate
inversion procedure is also provided there [176],
which utilizes a Kramers–Kronig relation to extract
(!) from the tunneling result. An inversion of
Im(! + iı) then removes
∗
from the procedure.
A variant of this, where the imaginary axis quantity
(i!
m
) is extracted directly from the tunneling I-V
characteristic,and then the imaginary axis equations
are inverted for ˛
2
F( ), also works [177], but the ac-
curacy requirements for a unique inversion are very
debilitating.
Optical Conductivity
In principle, any spectroscopic measurement will
contain a signature of ˛
2
F( ). In particular, sev-
eral attempts have been made to infer ˛
2
F( )from
optical conductivity measurements in the supercon-
ducting state [178–180]. In this section we describe
a procedure for extracting ˛
2
F( )fromthenormal
state [181].
A common method to determine the optical con-
ductivity is to measure the reflectance [182] as a
function of frequency, usually at normal incidence.
The reflectance, R( ), is defined as the absolute ratio
squared of reflected over incident electromagnetic
wave amplitude. The complex reflectivity is defined
by
r( ) ≡ R
1/2
( )exp(i()) , (3.84)
where ( ) is the phase, and is obtained through a
Kramers–Kronig relation from the reflectance [182]
( )=
∞
0
ln R(
)−lnR( )
2
−
2
d
. (3.85)
The complex reflectivity is related to the complex in-
dex of refraction,n( ),
r( ) ≡
1−n( )
1+n( )
, (3.86)
which, finally, is related to the complex conductivity,
( ) (using the dielectric function, ( )):
( ) ≡ n
2
( )=
∞
+
4i ( )
, (3.87)
where
∞
is the dielectric function at high frequency
(in principle, for infinite frequency this would be
unity). It is through such transformations that the
“data” is often presented in “raw” form. Nonethe-
less, assumptions are required to proceed through
these steps; for example, Eq. (3.85) indicates quite
clearly that the reflectance is required over all posi-
tive frequencies. Thus extrapolation procedures are
required at low and high frequencies; a more thor-
ough discussion can be foundin [183]; see also [184].
For this review,we will consider both static impu-
rities and phonons as sources of electron scattering.
Both contribute to the optical conductivity, and can
be treated theoretically either with the Kubo formal-
ism or with a Boltzmann approach [81]. In the Born
approximation the result for the conductivity,in the
normal state, at zero temperature, is [179]:
( )=
!
2
P
4
i
0
d!
1
+ i/ − £(!)−£( − !)
, (3.88)
where
£(!)=
∞
0
d§˛
2
F(§)ln
§ − !
§ + !
− i
|!|
0
d§˛
2
F(§)
(3.89)
is the effective electron self-energy due to the
electron–phonon interaction. The spectral function
that appears in Eq. (3.89) is really a closely related
function, as has been discussed by Allen [179] and
Scher [185]. For our purposes we will treat them
identically.The other two parameters that enter these
expressions are the electron plasma frequency, !
P
,
and the (elastic) electron-impurity scattering rate,
1/.
Equation (3.88) has been written to closely resem-
bletheDrudeformas
Dr
( )=
!
2
P
4
i
+ i /
. (3.90)
102 F. Marsiglio and J.P. Carbotte
The equation could well be recast in this form with
a frequency-dependent scattering rate and effective
mass (in the plasma frequency) [186]. Equations
(3.88) and (3.89) make clear that the optical conduc-
tivity is given by two integrations over the electron–
phonon spectral function. One would like to “un-
ravel” this information as much as possible before
attempting an inversion, so that, in effect, the signal
is “enhanced”. To this end one can attempt various
manipulations [187–189].
As a first step one can make a weak coupling type
of approximation to obtain [181] the explicit result:
˛
2
F( )=
1
2
!
2
P
4
d
2
d
2
Re
1
( )
. (3.91)
Note that the conductivity data,including a measure-
ment of the plasma frequency, provides us with both
the shape and magnitude of ˛
2
F( ). Equation (3.91)
works extremely well, as Fig. 3.20 shows, in the case
of Pb. It tells us that, with a judicious manipulation
of the conductivity data, the underlying electron–
phonon spectral function emerges in closed form.
The very simple formula (3.91) introduces some er-
rors — it was derived with some approximations —
Fig. 3.20. ˛
2
F( ) for Pb (solid curve) vs. , along with the
estimates obtained from (3.91) with an impurity scatter-
ing rate, 1/ =1meV(dotted)and10meV(dot–dashed).
These are both qualitatively quite accurate,before they be-
come negative at higher frequencies. Also plotted is the
result (dashed cur ve, indiscernible from the solid curve)
obtained from a full numerical inversion, as described in
the text.Taken from the second reference in [181]
as can be seen in Fig. 3.20. In fact, a full numerical
inversion will also succeed [190,191]; the first ref-
erence requires a Newton–Raphson iteration tech-
nique, while the second uses an adaptive method (in
the superconducting state). Equation (3.91) was first
applied to K
3
C
60
[181] to help determine whether or
not this class of superconductor was driven by the
electron–phonon interaction. The result is shown in
Fig. 3.21 and provides convincing evidence that the
alkali-doped fullerene superconductorsare driven by
the electron–phonon mechanism. We will return to
these superconductors in a later section, and further
examine the optical conductivity in the supercon-
ducting state in another section.
Before leaving this section we wish to discuss
some more recent work [195] which utilizes the
Memory function M(!)=1/
op
(!)−i!
op
(!).The
real and imaginary parts of this function are related
by a Kramers-Kronig relation, and one can write, for
the optical conductivity,
(!)=
!
2
P
4
i
! + iM(!)
. (3.92)
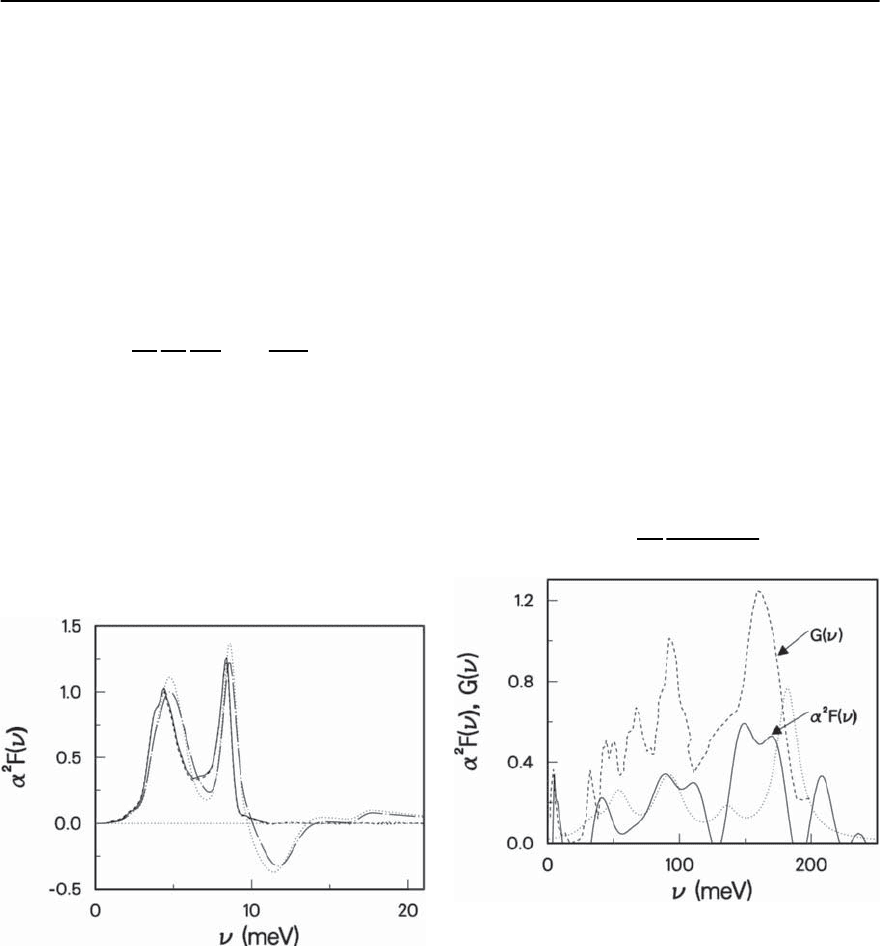
Fig. 3.21. The ˛
2
F( )forK
3
C
60
(solid curve) extracted from
the reflectance data of Degiorgi et al. [192], using (3.91).
For purposes of analysis we have omitted the negative
parts. The neutron scattering results from [193] (dashed
curve) are also shown. Clearly the energy scale in ˛
2
F( )
matches that of the phonons, and some of the peaks even
line up correctly. Finally, the dotted curve comes from an
analysis of photoemission data [194], where we have arbi-
trarily broadened the phonon spectrum with Lorentzian
line-shapes. Taken from the second reference in [181]
3 Electron–Phonon Superconductivity 103
In this way 1/
op
(!)=
!
2
P
4
Re(1/ (!)) is interpreted
as an optical scattering rate and ![1 +
op
(!)] =
−
!
2
P
4
Im(1/ (!)) is ! times the optical mass ra-
tio,
m
∗
(!)/m
op
,and
op
(!)istheopticalmass
renormalization. Using ordinary perturbation the-
ory to second order in the electron-phonon interac-
tion Allen [179] obtained, at zero temperature,
1/
op
(!)=
2
!
!
0
d§˛
2
F(§)(! − §)+1/
imp
.
(3.93)
Note that Eq. (3.91) was derived through differ-
ent considerations, but is completely consistent with
Eq. (3.93). If we consider the case of a single Einstein
mode, at frequency !
E
,weobtain
1/
op
(!)=
1
!
E
! − !
E
!
for ! > !
E
,
0 for ! < !
E
.
(3.94)
This is to be contrasted with the quasiparticle scat-
tering rate given by Eq. (3.26),
−2£
2
(! + i ı) ≡ 1/
qp
(!)
= !
E
(|!| − !
E
) .
(3.95)
Both the optical and the quasiparticle scattering
are zero for frequencies below !
E
.Beyondthisfre-
quency, however, the quasiparticle scattering rate
jumps abruptly to a value !
E
,andremainscon-
stant at that value, whereas the optical scattering rate
increases continuously from zero and reaches the
value !
E
asymptotically for ! →∞.Thus,we
see through this simple example that boson struc-
ture is expected to appear in a more singular fashion
in the quasiparticle scattering rate compared to that
in the optical scattering rate. This is expected since,
according to Eq.(3.89) only the first derivative of the
quasiparticle scattering rate with respect to ! is re-
quired to give ˛
2
F(!), whereas Eq. (3.91) indicates
that a second derivative is required to extract the
spectral function from the optical scattering rate.
An application of the Kramer-Kronig relation to
Eq. (3.94) gives
!
op
(!)=−!
E
×
log
!
E
+ !
!
E
− !
+
!
E
!
log
!
2
E
− !
2
!
2
E
;
(3.96)
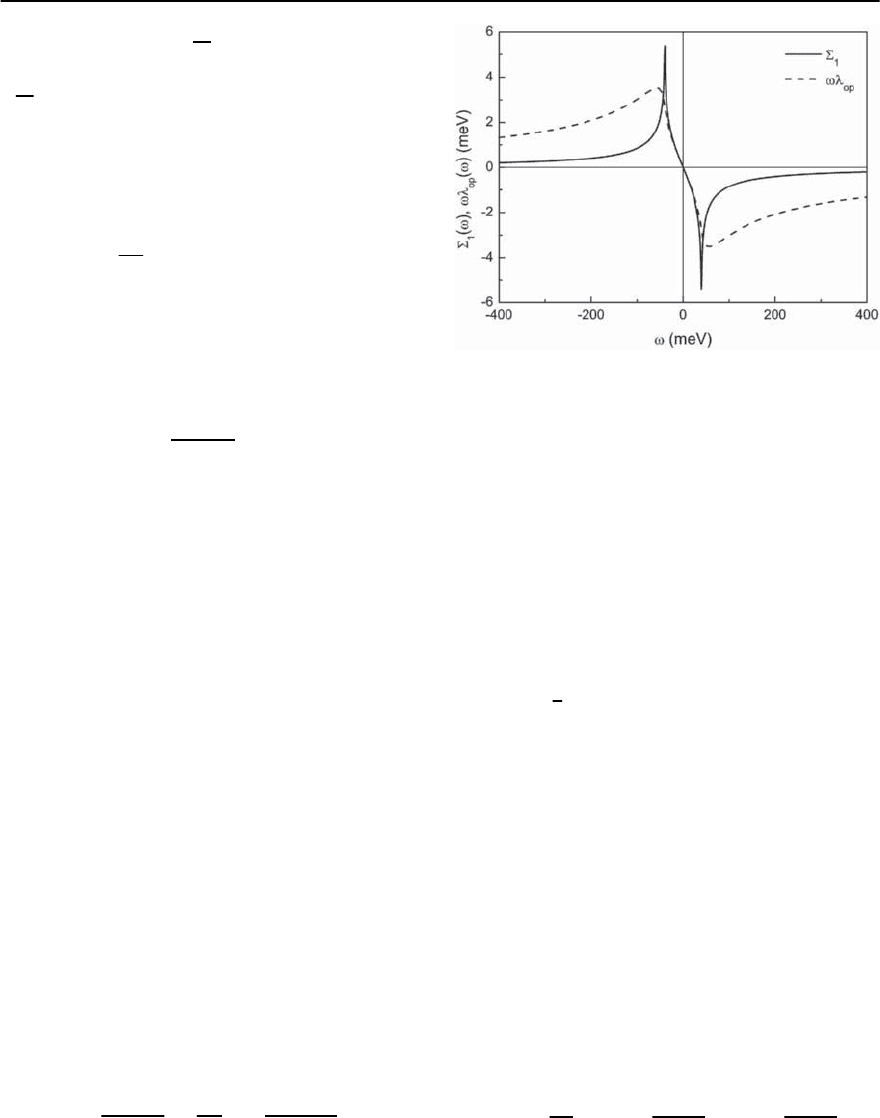
Fig. 3.22. A comparison of the real part of the quasipar-
ticle self-energy with the corresponding optical quantity,
!
op
(!) vs. frequency.Taken from [195]
this is to be contrasted with the expression for
the real part of the quasiparticle self-energy given
in Eq. (3.26). In Fig. 3.22 we compare £
1
(!)and
!
op
(!) as a function of frequency. The solid curve
represents the real part of the self-energy and dis-
plays a logarithmic singularity at ! = !
E
,whilethe
dashed curve for the corresponding optical quan-
tity is much less singular (note that Eq. (3.96) does
not contain a singularity, though its slope does). In
fact the latter quantity has a maximum/minimum
at ! = ±
√
2!
E
. For this figure, !
E
=40meVand
!
E
/2 = 1 meV.Again we conclude that boson struc-
ture that can in principle be identified in both the
self-energy and in optical properties has the more
pronounced signature in the quasiparticle dynam-
ics [195].
Equation (3.24), valid for any frequency and any
temperature,can easily be written for a general spec-
tral function,˛
2
F(§) [12]. The quasiparticle scatter-
ing rate is given by
1/
qp
(!) ≡ −2£
2
(T, !)=
∞
0
d§˛
2
F(§) (3.97)
×
2coth
§
2T
−tanh
! + §
2T
+tanh
! − §
2T
.
104 F. Marsiglio and J.P. Carbotte
Shulga et al. [186] have obtained the approximate
equation
1/
op
(!)=
!
∞
0
d§˛
2
F(§)
×
2!coth
§
2T
−(! + §)coth
! + §
2T
(3.98)
+(! − §)coth
! − §
2T
.
Note that this expression properly reduces to Allen’s
equation (3.93) in the limit of zero temperature.
The corresponding real parts can be obtained from
Eqs. (3.97) and (3.98) through Kramers-Kronig
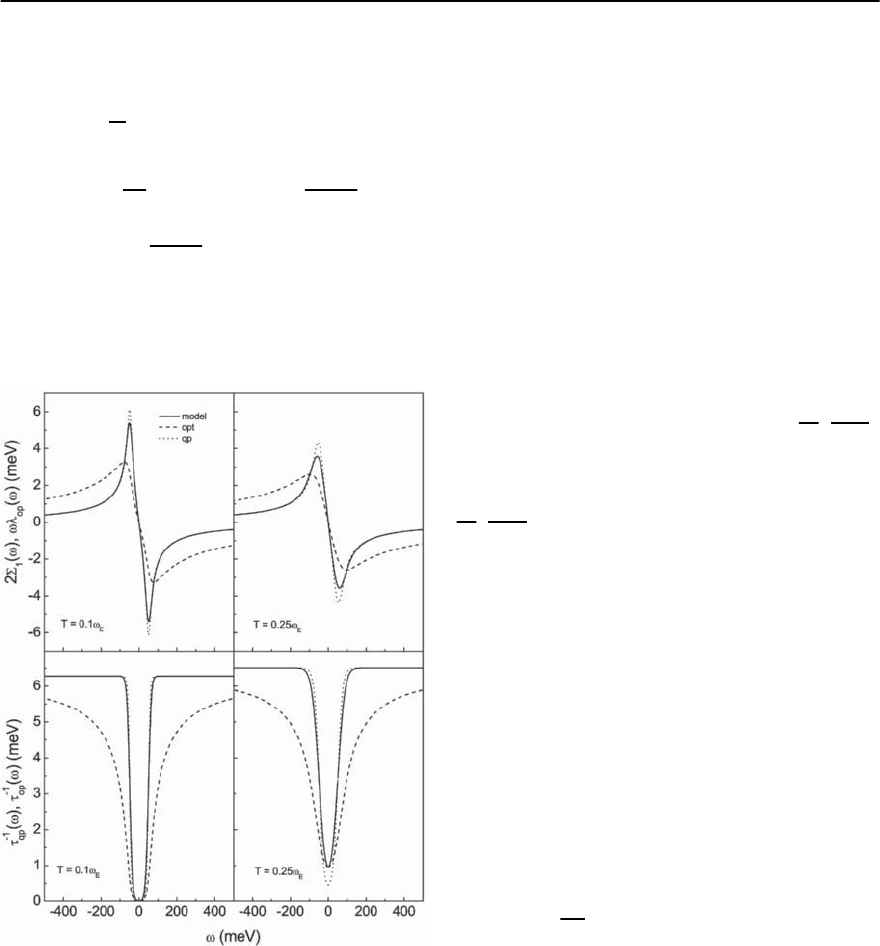
Fig. 3.23. A comparison of the real part of the self-energy
with the corresponding optical quantity, !
op
(!) vs. fre-
quency (top frames), along with the corresponding scatter-
ing rates (bottom frames ). The left-hand side frames are
for T =0.1!
E
and the right-hand side frames are for
T =0.25!
E
.Thesolid curves are for the model scatter-
ing rate defined in the text.An Einstein spectrum was used
with !
E
=40meVand!
E
/2 = 1 meV. Taken from [195]
transformations. Results for both real (top frame)
and imaginary (bottom frame) parts are given in
Fig.3.23 for T =0.1!
E
(left side) and forT =0.25!
E
(right side). Note that temperature does smear out
the signature of the boson structure in these quan-
tities; nonetheless, for the Einstein spectrum used
here, the structure remains apparent, even at the
higher temperature. In all cases the quasiparticle
(optical) properties are denoted by dotted (dashed)
curves. Figure 3.23 shows that the quasiparticle and
optical properties behave in quantitative and even
qualitative different ways.
Comparing such results obtained from optics with
those obtained, for example, from Angle Resolved
Photoemission Spectroscopy (ARPES) is therefore
difficult. The authors of [195] noted that at T =0
Allen’s approximation (Eq. 3.93) gives for
d
d!
!
op
(!)
precisely 1/
qp
(!) obtained from the self-energy
equation (3.89). They therefore defined a quan-
tity (termed “model” scattering rate) as 1/
M
(!) ≡
d
d!
!
op
(!)
, which can be constructed directly from
optical data. This can be compared with 1/
qp
(!)
obtained from ARPES. Of course these are only nec-
essarily equal at T = 0. To test this comparison at
finite temperature we can obtain 1/
M
(!)tohighac-
curacy by using Eq.(3.98); its corresponding realpart
can be obtained by Kramers-Kronig transformation.
The results are plotted as solid curves in Fig. 3.23.
These agree remarkably well with the results for the
quasiparticle self-energies (dotted curves) at finite
temperature.
These results are modified when an energy-
dependent bare EDOS is used [143]. Using a gener-
alization of Allen’s formula for the optical scattering
rate, Mitrovi´c and Perkowitz obtained
1/
op
(!)=
2
!
!
0
d§˛
2
tr
F(§)
!−§
0
d n
S
(), (3.99)
where n
S
() ≡
˜
N()+
˜
N(−)
/2isthe“sym-
metrized” renormalized EDOS. Note that we use
˛
2
tr
F(§) in this expression, which is more accu-
rate than simply using the electron-phonon spectral
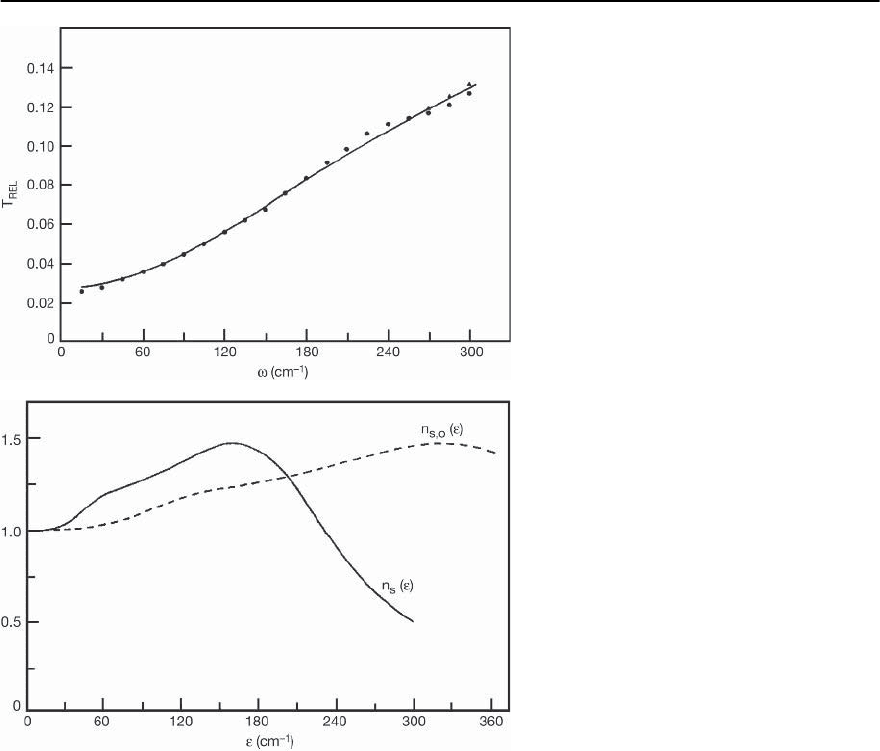
function. In Fig. 3.24 we show the fit (solid curve)
obtained to the data (solid circles) on the suitably
normalized transmission through the V
3
Si thin film.
3 Electron–Phonon Superconductivity 105
Fig. 3.24. Comparison of experiment (solid
dots) for a transmission through V
3
Si thin film
with theoretical fit (solid curve) using Eliash-
berg theory with a non-constant bare EDOS as
discussed in the text. Taken from [143]
Fig. 3.25. The renormalized EDOS (solid curve)
along with the unrenormalized EDOS (dashed
curve)forV
3
Si.See [143] for more details
Thefit isvery good.Using Eq.(3.99)thesymmetrized
renormalized EDOS was obtained and plotted in
Fig. 3.25 [143]. For the electron-phonon interaction,
the electron-phonon spectral function was taken to
be proportional to the measured phonon density of
states for V
3
Si with = 1. The solid curve in Fig. 3.25
is to be compared with the dashed curve (denoted
by n
s0
()) which is the bare EDOS. This latter func-
tion is broader than the renormalized one, as ex-
pected from the discussion in a previous subsection.
Mitrovi´c and Perkowitz also note that inversion of
the data in Fig. 3.24 based on a constant bare EDOS
leads to an ˛
2
tr
F(§) which disagrees strongly with
the known phonon distribution, F(§) [196] for V
3
Si.
In particular, a prominent new peak is found near
5 meV that is not observed in the neutron spec-
trum. This observation constitutes strong evidence
for the energy dependence in N()inV
3
Si. Moreover,
this is expected both from band structure calcula-
tions [132] and from the measured strong degrada-
tion of T
c
with disorder [137,197]. Further analysis
of other data in the superconducting state provides
more evidence for this picture [198].
Finally, returning to tunneling in the supercon-
ducting state,the effect of a non-constant bare EDOS
can be summarized through the following equations
(at T = 0) [139]:
106 F. Marsiglio and J.P. Carbotte
(!)Z(!)=
∞
0
d!
˜
N
(!
)
×
K
+
(!, !
)−
∗
(!
c
− !
)
!(1 − Z(!)) =
∞
0
d!
˜
N
Z
(!
)K
−
(!, !
)
(!)=
∞
0
d!
˜
N
(!
)K
+
(!, !
), (3.100)
with (!) ≡ (!)/Z(!),
K
±
(!, !
)=
∞
0
d§˛
2
F(§)
×
1
!
+ ! + § + i ı
±
1
!
− ! + § − iı
,
(3.101)
and
˜
N
Z
(!)=−
1
Im
+∞
−∞
d
N()
N()
!Z(!)
D(, !)
˜
N
(!)=
1
Im
+∞
−∞
d
N()
N()
+ (!)
D(, !)
˜
N
(!)=−
1
Im
+∞
−∞
d
N()
N()
(!)
D(, !)
, (3.102)
with
D(, !) ≡ !
2
Z
2
(!)n−
2
(!)−(+(!))
2
. (3.103)
Note that here, following the original reference, we
have momentarily dropped the iı in the arguments
of the various functions. Using the same parame-
ters as used in the normal state for Nb
3
Sn, Mitrovi´c
and Carbotte [139] calculated the gap function (!)
and obtained the conductance (at T = 0), given by
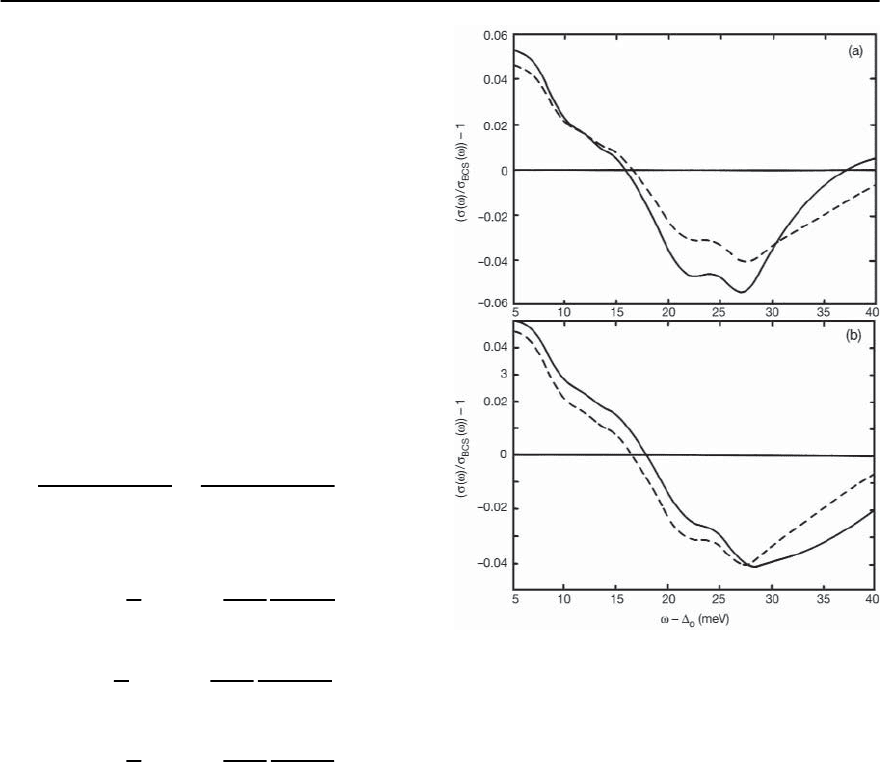
Eq. (3.82). The result is shown in Fig. 3.26 as a func-
tion of ! −
0
,where
0
is the single electron gap
defined by Eq. (3.83). The top (bottom) frame is for
a peak (valley) in the bare EDOS, and the results are
Fig. 3.26. Normalized tunneling conductance (solid curves)
for (a) a peak and (b) a valley in the bare EDOS. The
dashed curves are obtained assuming a constant bare EDOS
equal to the value at the chemical potential. Reproduced
from [139]
given by the solid curves.The dashed curves were cal-
culatedassuming a constantEDOS withN()=N()
for all . In the inserts of Fig. 3.27 details of the two
bare EDOS are shown. While the conductance (!)
vs. ! is significantly affected by the energy depen-
dence of the bare EDOS, it is difficult to differenti-
ate the boson structure (which is also present when
a constant bare EDOS is used) from the structure
due to the bare EDOS. Mitrovi´c and Carbotte in-
verted the data in Fig. 3.26 assuming a constant bare
EDOS [139]. The results are shown in Fig. 3.27. The
solid curves are the results of the inversion and the
dashedcurves arethe actual ˛
2
F(§) usedto compute
the conductance in the first place.While these agree
reasonably well at low frequencies the solid curve
