Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.

3 Electron–Phonon Superconductivity 107
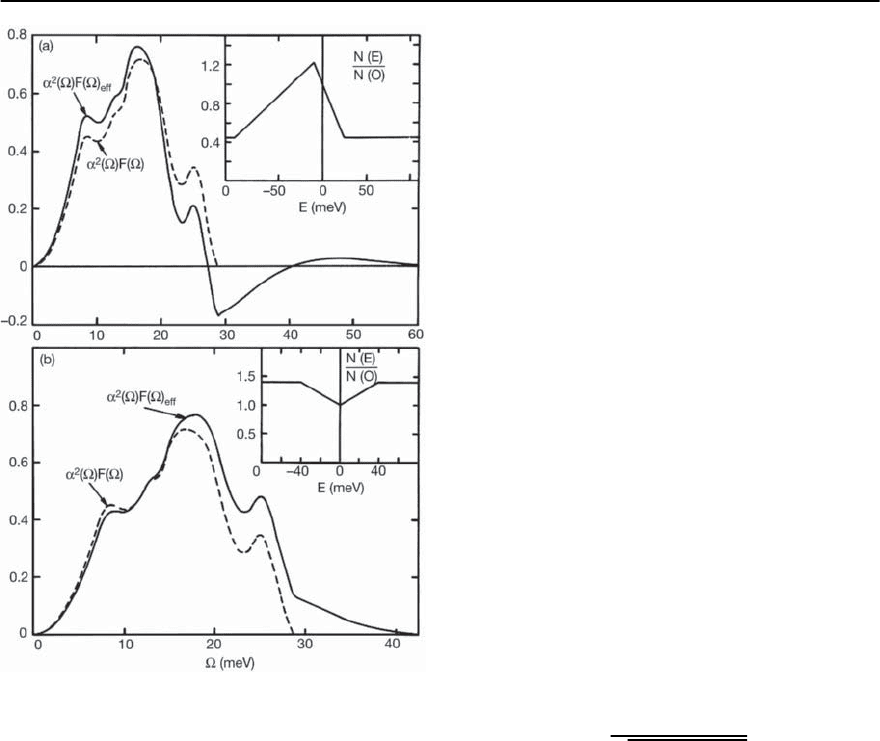
Fig. 3.27. Effective electron–phonon spectral functions ob-
tained through inversion of the conductance calculated
from Eliashberg theory with non-constant bare EDOS, as
indicated. The inversion, however, was carried out assum-
ing a constant bare EDOS. The input ˛
2
F(§)isindicated
by the dashed line,andtheinsets indicate the input bare
EDOS.Reproduced from [139]
shows a negative (positive) tail beyond the maxi-
mum phonon frequency for a peak (valley) in the
bare EDOS. The lesson learned is that an energy de-
pendent bare EDOS will cause extra structure in the
conductance. In one case (positive peak) the struc-
ture will lead to an unphysical result,namely a nega-
tive tail in the inverted ˛
2
F(§), but in the other one,
we have no way of knowing if the inverted ˛
2
F(§)is
reasonable or not (unless, say, neutron spectroscopy
indicates definitively that there are no phonons in
this energy region).
Furtherworkinthisareacanbeconsultedthrough
the reviews mentioned earlier. We also mention the
work of Schachinger et al. [199,200] on thermody-
namic properties based on a generalized free energy
formula derived in [139].A more recent study of the
effect of a more realistic bare EDOS on the tunneling
characteristics of Nb
3
Sn is given in [201].
Photoemission Spectroscopy
Angle resolved photoemission spectroscopy
(ARPES) has been very successful in providing de-
tailed microscopic information about the electronic
properties of the cuprate materials, as described in
another chapter of this book. Photoemission spec-
troscopy has also been successfully applied to several
other electron-phonon superconductors (see [202]
for a review). Without angular resolution photoe-
mission spectroscopy (PES) measures a convolution
of the electron density of states, N(!
), multiplied
by the Fermi function f (!
), with an instrument
resolution function, R(!, !
), characterized by a
peaked distributionwith a width.Here,we follow the
literature [203] and use a Gaussian with width 2.8
meV.Results from Reinert et al.[203] are reproduced
in Fig. 3.28 for a polycrystalline lead sample, taken
at T =4.5 K. The solid black curve is the electron
density of states in the superconducting state,
N(!)=Re
|!|
!
2
−
2
(T, !)
, (3.104)
multiplied by the Fermi function and convoluted
with R(!, !
), where (T, !)isthegapfunction
given by Eliashberg theory. The data (indicated by
thesymbols) agree remarkably well withthistheoret-
ical expectation. The inset highlights the frequency
regime where phonon structure occurs, and shows
excellent agreement with the calculations. These are
basedona tunneling-derivedmodelfor ˛
2
F(§)inPb
shown in the inset of Fig. 3.29 [203].The main frame
of Fig. 3.29 shows data for the electron linewidth
as a function of temperature. The curves are from
Eliashberg theory, and are given by the imaginary
part of the self-energy at zero frequency and at the
maximum phonon frequency, 12 meV (they have
both been shifted upwards because of an unknown
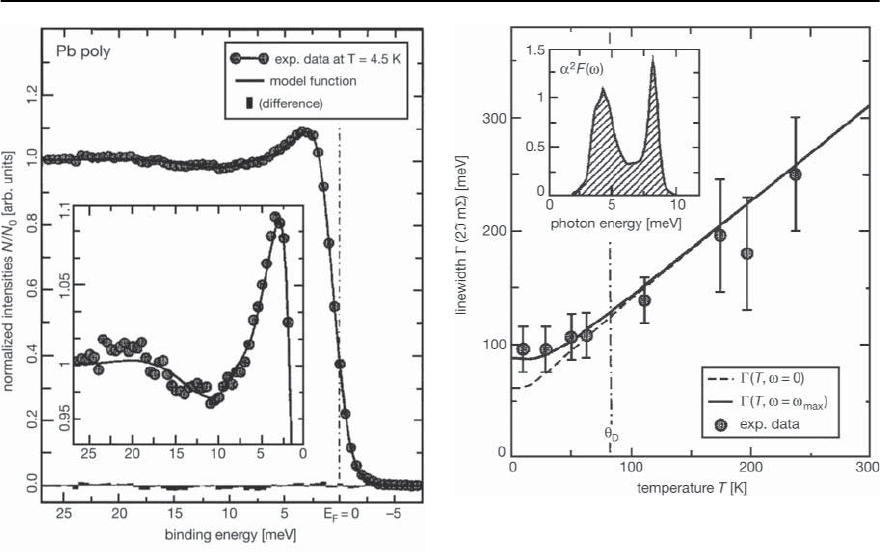
108 F. Marsiglio and J.P. Carbotte
Fig. 3.28. Normalized photoemission intensity in the su-
perconducting state vs. energy. The experimental data are
given by the circles, and a BCS-like EDOS convoluted with
other functions as described in the text is given by the solid
curve. The agreement is very good.Reproduced from [203]
amount of impurity scattering).Chainani et al.[204]
have obtained similar data in Pb. They also show the
temperature evolution of the PES spectrum in Nb
(for 5.3K < T < 10.3K), which illustrates how the
gap disappears as the temperature is raised through
T
c
. These results illustrate that photoemission spec-
troscopy is being used in much the same spirit as
tunneling spectroscopy pioneered by McMillan and
Rowell in the 1960s [50].An earlier study of the A15
compound Nb
3
Al is given in [205]. Other measure-
ments are for V
3
Si [206], MgB
2
[207–209], Ba-K-Bi-
O [210] and in the heavy fermion CeRu
2
[211].
Fig. 3.29. Temperature dependence of the quasiparticle
linewidth as a function of temperature. Data is indicated
by circles with error bars.Theory has used a fitted impurity
contributionto match the magnitude of the data. The inset
shows the spectral function for Pb used to achieve such a
fit. Reproduced from [203]
3.4 The Critical Temperature and
the Energy Gap
Perhaps the most important property of a supercon-
ductor isthecritical temperature,T
c
.Forthisreasona
considerable amount of effort has been devoted both
towards new materials with higher superconducting
T
c
, and, on the theoretical side, towards an analytical
solution of the linearized Eliashberg equations (set
m
to zero, where it appears in the denominator in
Eqs. (3.55)–(3.58) ) for T
c
(see [10,12] for reviews);
the experimental “holy grail” has enjoyed some suc-
cess, particularly in the last 15 years; the theoretical
goal has had limited success. In fact numerical so-
lutions are so readily available at present, that the
absence of an analytical solution is not really debili-
tating to understanding T
c
.
In the conventional theory there are two input
“parameters”: a function of frequency, ˛
2
F( ), about

3 Electron–Phonon Superconductivity 109
whichwehavealreadysaidmuch,and
∗
(!
c
),anum-
ber which summarizes the (reduced) Coulomb re-
pulsion experienced by a Cooper electron pair. The
focus of this chapter will be the effect of size and
functional form of ˛
2
F( )onT
c
.
3.4.1 Approximate Solution: The BCS Limit
The first insight into T
c
comes from reducing the
Eliashberg theory to a BCS-like theory. This is ac-
complished by approximating the kernel
(i!
m
− i!
m
) ≡
∞
0
2˛
2
F( )
2
+(!
m
− !
m
)
2
(3.105)
by a constant as long as the magnitude of the two
Matsubara frequencies are within a frequency rim of
the Fermi surface [123], taken for convenience to be
!
c
, the cutoff used for the Coulomb repulsion,
∗
.
That is,
(i!
m
−i!
m
)=
1
for both |!
m
|, |!
m
| < !
c
,
0otherwise,
(3.106)
where ≡ (0) has already been defined in
Eq. (3.21). Then, the linearized version of Eq. (3.55)
(with A
0
(m
) = 1), for the renormalization function,
Z(i!
m
), reduces to
Z(i!
m
) ≈ 1+ . (3.107)
Using this and solving the linearized version of
Eq.(3.57) for the pairing function yields
1+
−
∗
=
!
c
2T
c
+
1
2
−
1
2
, (3.108)
where (x) is the digamma function. The cutoff in
these equations is along the Matsubara frequency
axis; this procedure is to be contrasted with the BCS
procedure, which introduced a cutoff in momentum
space. The former is more physical, insofar as the
true electron–phonon interaction comes from retar-
dation effects, which occur in the temporal domain;
hence the cutoff should occur in the frequency (ei-
ther real, or imaginary) domain. In practice, the two
procedures are connected, so they produce the same
physical equation in the weak coupling limit.
Returning to Eq. (3.108), for large x, (x) ≈
log (x), so, in the weak coupling limit (T
c
!
c
),
we obtain a BCS-like equation,
T
c
=1.13!
c
exp
−
1+
−
∗
. (3.109)
This equation has essentially summarized all the de-
tailedinformation containedin the electron–phonon
spectral function ˛
2
F( ) into two parameters, and
!
c
. The mass enhancement parameter, ,isasimple
moment of ˛
2
F( ) (see Eq. (3.21)), while the param-
eter !
c
physically is meant to represent some typ-
ical phonon frequency. In more refined treatments
[123,212], !
c
is given by some moment of ˛
2
F( )as
well. For example, in [123], the logarithmic average
is used to define !
ln
(see Eq. (3.71)), a quantity we
shall use extensively in the following sections. They
modified the McMillan equation [212] to read
k
B
T
c
=
!
ln
1.2
exp
−
1.04(1 + )
−
∗
(1 + 0.62)
. (3.110)
A derivation of this equation is given in Refs.
[123,212].
3.4.2 Maximum T
c
, Asymptotic Limits,
and Optimal Phonon Spectra
Equation (3.109)(or (3.110))describes the weak cou-
pling limit of Eliashberg theory reasonably well. It
errs in the strong coupling limit; for example, it
predicts that T
c
saturates as increases, whereas
the Eliashberg equations themselves predict that T
c
grows indefinitely with . (Of course, physically we
know that Eliashberg theory gets this limit com-
pletely wrong; T
c
should peak at some point and
then decrease to zero as the coupling strength in-
creases. That an approximation to Eliashberg theory
improves upon this doesn’t justify that approxima-
tion; it simply means two errors have undone one
another to get closer to the “right answer”.) Asymp-
totic results from Eliashberg theory can be obtained
correctly and analytically [10,123] through a variety

110 F. Marsiglio and J.P. Carbotte
of arguments. (D. Rainer first obtained the asymp-
toticresult noted in the text in 1973 (private commu-
nication).) The methodology based on scaling theo-
rems is particularly powerful, and has been applied
to other thermodynamic properties as well [10].
The correct asymptotic result for T
c
is [123]:
T
c
=0.183
√
!
E
, (3.111)
as →∞. In obtaining Eq. (3.111), an Einstein
spectrum has been assumed (this is not required),
which in turn is characterized by two parameters:
the weight, A ≡ !
E
/2, and the frequency, !
E
.In
writing Eq. (3.111), one tacitly has assumed that the
parameter ≡ 2A/!
E
is increased while keeping
the frequency !
E
fixed.In reality,the two parameters
are not independent — this is the main point of the
article by Cohen and Anderson [213]. For example,
often phonon softening occurs because the coupling
strength increases. In fact, this is made explicit in
McMillan’s definition [212] of :
≡
N(
F
)˛
2
M!
2
E
, (3.112)
where N(
F
) is the electron density of states at the
Fermi energy, M is the ionic mass, and ˛
2
is the
electron–ion coupling referred to in the Holstein
Hamiltonian, Eq. (3.4) (in a more realistic electron–
phonon Hamiltonian, ˛
2
would be given by a Fermi
surface average of the electronic matrix element of
thechangeincrystalpotentialasoneatomismoved
[212]).
To determine what the optimal phonon frequen-
cies actually are, functional derivatives were intro-
duced [121]. These had already been utilized ex-
tensively as an iterative aid in inverting tunneling
data with the Eliashberg equations [50]. The most
commonly used functional derivative is that of T
c
with respect to infinitesimal changes in ˛
2
F( ), with
fixed area, A ≡
∞
0
d˛
2
F( ), first computed by
Bergmann and Rainer [121]. An approximate result,
derived in [214], is given by the expression
ıT
c
ı˛
2
F(§)
=
1
1+
∞
n=1
4
¯
§
¯
§
2
+4
2
n
2
B
n
, (3.113)
where
¯
§ ≡ §/k
B
T
c
,andtheB
n
are numbers given by
Fig. 3.30. The universal function G(
¯
§) as a function of nor-
malized phonon energy
¯
§ = §/T
c
which enters the curve
for the functional derivative of T
c
with respect to ˛
2
F(!)
in the
ŸŸ
model of [214],from which this figurewas taken
B
n
=
n
m=1
1
n
2
2m −1
+
2
(2m −1)
2
−
2
4
. (3.114)
This function (which is universal) is shown in
Fig. 3.30, and reflects well the generic behaviour of
the more precise calculation.It illustrates that the op-
timal phonon frequency lies at some finite frequency
(i.e. non-zero, and non-infinite),which is a factor of
order 10 times the critical temperature. Thus if one
could imagine shifting small amounts of weight in
˛
2
F( )aroundthenT
c
would increase if spectral
weight is shifted either from very high or from very
low frequencies towards frequencies near the max-
imum of the curve shown in Fig. 3.30. The reason-
ing above leads naturally to the concept of an opti-
mum spectrum, first determined by Leavens [215],
and elaborated upon in Refs. [216–220]. In an op-
timum spectrum calculation, one imagines having
a fixed area of ˛
2
F( ), and asks at what frequency
it would best be situated in order to optimize some
particular property.An appropriate scaling of thelin-
earized Eliashberg equations for an Einstein phonon
spectrum with frequency !
E
leads to the result
T
c
/A = f ( ¯!
E
,
∗
) , (3.115)
where A is the area, ¯!
E
≡ !
E
/A,andf is a univer-
sal function of ¯!
E
, to be determined numerically for
each choice of
∗
(a very weak A dependence in the

3 Electron–Phonon Superconductivity 111
Fig. 3.31. The constant c(
∗
)intherelationk
B
T
c
= c(
∗
)A
for the maximum T
c
associated with a given A as a function
of
∗
. Placed on the same figure (solid do ts) are the results
for T
c
/A obtained in the case of many strong coupling su-
perconductors forwhich ˛
2
F(!) is known from tunneling
spectroscopy. The solid points all fall below the maximum
curve as they must.Adapted from [215]
cutoff associated with
∗
has been neglected). The
resultisacurvewithamaximumat ¯!
E
≈ 1; placing
a spectral function at this frequency will yield the
maximum T
c
. This procedure yields a result,
T
c
≤ Ac(
∗
) , (3.116)
where c(
∗
)isafunctionof
∗
shown in Fig. 3.31.
Also shown are data from many superconductors for
which˛
2
F( ) is known from tunneling spectroscopy,
all of which fall below the optimum curve. Interest-
ingly, some superconductors have a critical tempera-
ture reasonably close to their optimal value. The last
few paragraphs demonstrate the usefulness of func-
tional derivatives in understanding the systematics
of T
c
.A variant of these results can easily be obtained,
which may shed even more light on T
c
systematics.
As we have already mentioned,the functional deriva-
tivediscussed involves the moving around of spectral
weight, subject to the condition that the area remain
constant.However,as Eq.(3.112) suggests,it is not the
area which likely remains constant while phonons
soften, but rather the area times a frequency. Hence,
one can define a different spectral function,
˛
2
G( ) ≡ ˛
2
F( ) , (3.117)
and take functional derivatives with respect to this
new function. The result is easily obtained from that
in Eq. (3.113),simply by dividing by §.Then
ıT
c
ı˛
2
G(§)
will peak at zero frequency, and it would seem that
it is always advantageous to decrease the phonon
frequency. Continuing this process will result in
a spectrum for which the calculation which gives
Eq. (3.113) is no longer valid, and one would have
to self-consistently calculate the functional deriva-
tive,numerically.To our knowledge this has not been
done for T
c
or any other superconducting property.
3.4.3 Isotope Effect
As already remarked in the Historical Developments
subsection, the discovery of an isotope effect on T
c
played an important role in the subsequent develop-
ment of the theory. In the BCS equation the isotope
effect is clear fromtheprefactor;phonon frequencies
for elemental superconductors are inversely propor-
tional to the square root of the ionic mass, and hence
the isotope coefficient ˇ is
ˇ ≡ −
d lnT
c
d ln M
=
1
2
. (3.118)
The last equality follows from Eq. (3.40), using the
fact that , as defined there, is independent of ion
mass.In the standard Eliashberg theory, as defined
by Eq. (3.21) remains independent of ion mass, and,
with
∗
≡ 0, we once again obtain ˇ =1/2. Compli-
cations can arise,for example,from a finite electronic
bandwidth [221], or from a non-constant density of
states near the Fermi level [222–224].
There are two other clear sources of deviation
from ˇ =1/2. One is that in non-elemental super-
conductors, an isotopic substitution for one of the
elementswill result in varying changes in T
c
,depend-
ing onhowtheelement being substitutedcontributes
to the important phonon modes. One then has to de-
fine partial isotope coefficients, defined by [225]
ˇ
i
≡ −
d ln T
c
d ln M
i
, (3.119)
where M
i
refers to the mass of the ith element. The
total isotope coefficient,ˇ
tot
≡
i
ˇ
i
,willsumto1/2

112 F. Marsiglio and J.P. Carbotte
(in the absence of
∗
). The total isotope coefficient
canalsobebrokendownbyfrequency,with
ˇ(!) ≡ ˛
2
F(!)
d
d!
!
2T
c
ıT
c
ı˛
2
F(!)
, (3.120)
and then
ˇ
tot
=
∞
0
d!ˇ(!) . (3.121)
Equation (3.121) is useful when phonon modes com-
ing from one of the elements are well separated from
those coming from the others, as exists, for example,
in the high temperature perovskites, since oxygen is
much lighter than the other elements, and hence is
chiefly responsible for the high frequency modes.Ex-
ample calculations can be found in Refs. [10,226].
The second source of deviation from ˇ =1/2is
because
∗
(!
c
) is non-zero. To understand why this
causes less of a reduction in T
c
(when a heavier mass
is substituted) recall that
∗
(!
c
) is reduced from
some larger value (!
B
) through the pseudopoten-
tial effect. That is, it is through retardation that a
weaker electron–phonon interaction can overcome
the stronger direct Coulomb repulsion. In analyti-
cal treatments this is often modelled by endowing
a mass dependency to the Coulomb pseudopoten-
tial through the cutoff [212].Forexample,inspection
of Eq. (3.79) shows a mass dependency if the cut-
off frequency !
c
is made to correspond to a phonon
frequency. Then one can derive, from the McMillan
equation for T
c
, Eq.(3.110), the following expression
for the isotope coefficient (assuming one element):
ˇ =
1
2
1−
1.04(1 + )(1 + 0.62)
[ −
∗
(1 + 0.62)]
2
∗2
. (3.122)
This result properly reduces to 1/2when
∗
=0,
and shows that the isotope coefficient is generally
reduced when
∗
isfinite.Infactitisclearfrom
Eq. (3.122) that the isotope coefficient is reduced for
both positi ve and negative
∗
.The isotope coefficient
is reduced for positive
∗
because, when you lower
the ionic mass,the increase in phonon frequency will
raise T
c
, but not as much as would be the case if the
Coulomb repulsion were not present. This is because
thediscrepancy in frequency scaleshasbeen reduced
slightly,and the retardation-induced attractiveinter-
action is not as large as before the isotopic substitu-
tion.On the other hand a negative
∗
represents some
unknown attractive non-phonon mechanism [226],
which contributesto T
c
.A weakening of the phonon-
induced attraction(throughanisotopicsubstitution)
reduces T
c
only partially, resulting again in a reduced
isotope coefficient.
A more accurate determination of the isotope co-
efficient can be obtained simply numerically, follow-
ing the prescription of Rainer and Culetto [225]. In
this case a cutoff is imposed on the Eliashberg equa-
tions, which is independent of (but much greater
than) the maximum phonon frequency. An isotopic
substitution results in only a shift in the phonon
spectrum, and a subsequent calculation of T
c
will
yield the isotope coefficient. This is physically more
transparent than the analytical approach described
above, as an isotope substitution does not alter (at
this level of theory) the direct Coulomb repulsion.
There is a substantial literature on the isotope
effect; much of the older results are summarized
in [168]. By 1969 many low T
c
superconductors had
been found, several of which had very low isotope
coefficients. These had, for the most part, been ex-
plained through detailed calculations [3,227], due to
the physicsoutlinedabove.It isworthnoting thatthis
explanation of the sometimes low isotope coefficient
observed was not universally accepted [228].
The discovery of the high temperature cuprate
materials prompted considerable activity concern-
ing the isotope coefficient, as is reviewed in [229].
The isotope coefficient displays some unusual dop-
ing dependence in the La
2−x
{Sr,Ba}
x
CuO
4−ı
systems,
but is essentially zero in the optimally doped 90 K
YBa
2
Cu
3
O
7−y
system. The question is, can a realis-
tic (and conventional) electron–phonon interaction
give rise to a 90 K superconductor with a near zero
isotope coefficient? A qualitative answer can be ob-
tained [230] through the use of the McMillan equa-
tion (3.110), (3.122). For a given electron–phonon
coupling, , and phonon frequency !
E
,onecande-
termine the required value of
∗
(!
c
)tofixT
c
from
Eq. (3.110) (assuming !
c
refers to a cutoff associ-
ated with the phonon spectrum). These parameters
can then be used in Eq.(3.122) to determine the iso-
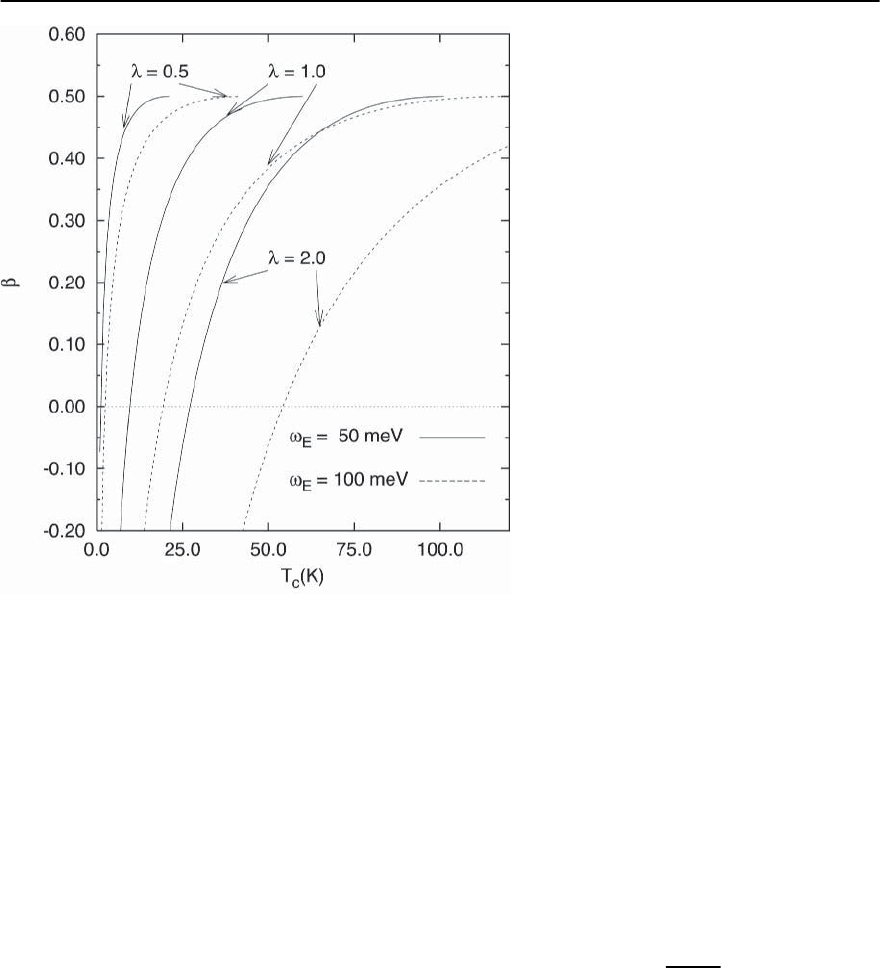
3 Electron–Phonon Superconductivity 113
Fig. 3.32. The isotope coefficient, ˇ,vs.T
c
,for
variousvaluesof and !
E
. Along each curve
T
c
changes because the Coulomb pseudopoten-
tial
∗
is being varied. These results show that a
low value of ˇ is difficult to attain with high-T
c
.
On the other hand, for low T
c
materials, it is not
so difficult
tope coefficient, ˇ. Some such results are plotted in
Fig. 3.32. To obtain the desired results for optimally
doped YBa
2
Cu
3
O
7−y
(T
c
≈ 90 K and ˇ ≈ 0) would
require high frequency phonons !
E
≈ 100 meV
with very strong electron–phonon coupling ( ≈ 5).
That such a coupling strength is unrealistic, particu-
larly for such very high frequency phonons, was dis-
cussed much earlier by Cohen and Anderson [213].
The qualitative validity of Fig. 3.32 has been ver-
ified by several numerical solutions to the Eliash-
berg equations [221,230,231].In particular, in [221]
a natural bandwidth cutoff was employed, with sim-
ilar results. In summary the conventional Eliashberg
theory can yield a near-zero isotope coefficient, pro-
vided T
c
is low.One must go beyond the conventional
framework to obtain a zero isotope coefficient with
T
c
≈ 90 K.
3.4.4 The Energy Gap
The existence of a single particle energy gap, al-
though not fundamental to superconductivity [232],
nonetheless has played an important role in our un-
derstanding of superconductivity. How an energy
gap arises in the I-V characteristic of a conven-
tional superconductor has already been discussed in
Sect. 4.4.3; there we focussed on extracting detailed
information about the mechanism. Here we turn our
attention to the gap, a much more prominent feature
in the experimental result, and learn what a particu-
lar value may imply about the superconductor.
The first step is to examine what occurs in BCS
theory. The order parameter is then given by a con-
stant,as written in Eq.(3.36). Suitable generalization
to the model interaction given by (3.106) yields
=2!
c
exp
−
1+
−
∗
, (3.123)
in the weak coupling limit.Thesolutionat finitetem-
perature is somewhat more complicated; it can be
obtained numerically, and shows the typical mean
field behaviour near T
c
[5]:
(T) ∝ (T
c
− T)
1/2
. (3.124)
114 F. Marsiglio and J.P. Carbotte
Near T = 0 the order parameter is exponentially flat
(see, for example, [233]):
(T) ≈ (0) − [2(0)T]
1/2
e
−(0)/T
. (3.125)
The order parameter is a real (i.e. not complex) num-
ber for all temperatures. (This is not to be taken as
a statement regarding the phase of the order param-
eter; we have ignored the phase up to this point, or,
equivalently, set it to zero. Rather, as is evident from
Eqs. (3.77) and (3.78), in Eliashberg theory the quan-
tity which takes on the role of the order parameter
acquires an imaginary part, whose significanceis as-
sociated with lifetime effects. ) Thus, Eq.(3.82) shows
that the dI/dV curve(which providesan image of the
density of states) will show an energy gap at (T)
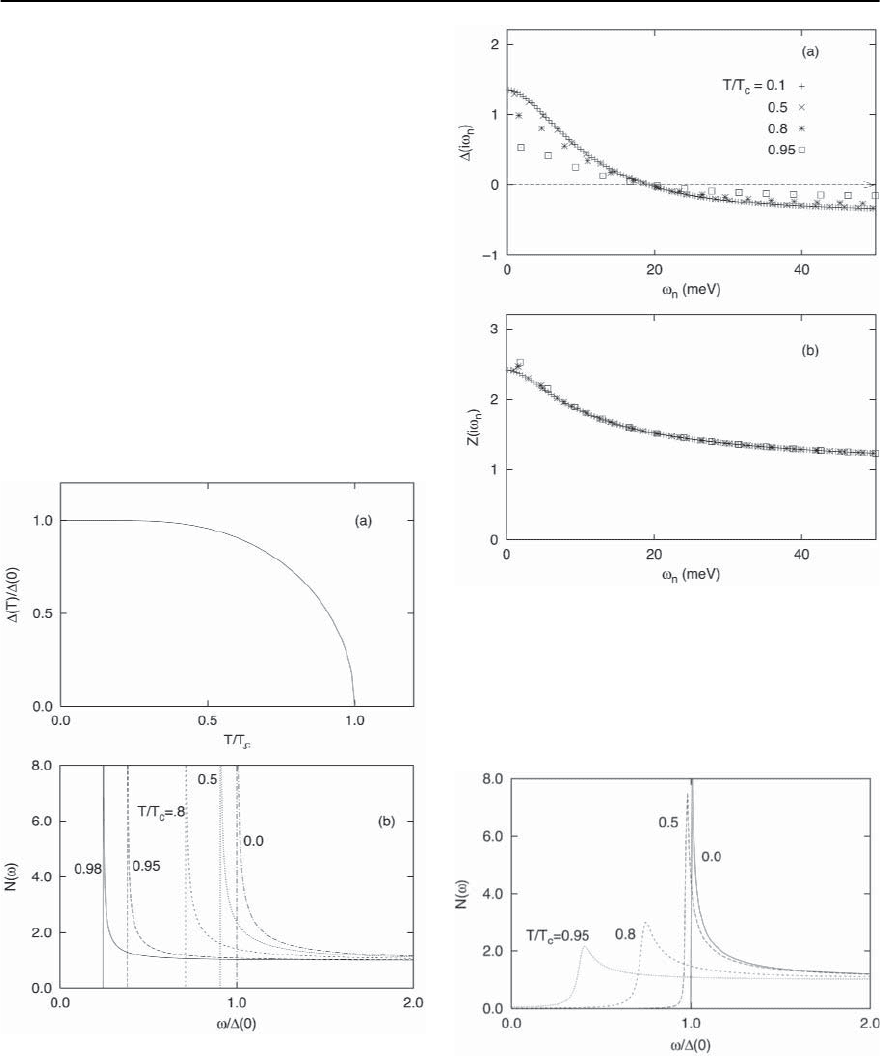
at each temperature. An illustration of the tempera-
ture dependence of the order parameter is given in
Fig. 3.33. (a) The temperature dependence of the BCS or-
der parameter, and (b) the resulting densities of states at
various temperatures below T
c
. The only effect of finite
temperatures on these latter curves is a reduced gap
Fig. 3.34.(a) (i!
n
)and(b)Z(i!
n
)vs!
n
,theFermionMat-
subara frequency, for various temperatures, as indicated.
Note that the curves are relatively smooth and featureless,
and at low temperatures little change occurs, except that
more Matsubara frequencies are present. In (a)theunits
of are meV. These were produced for Pb
Fig. 3.35. Calculated densities of states of Pb for various
temperatures. In contrast to the BCS case (Fig. 3.33b), at
high temperatures there is considerable smearing
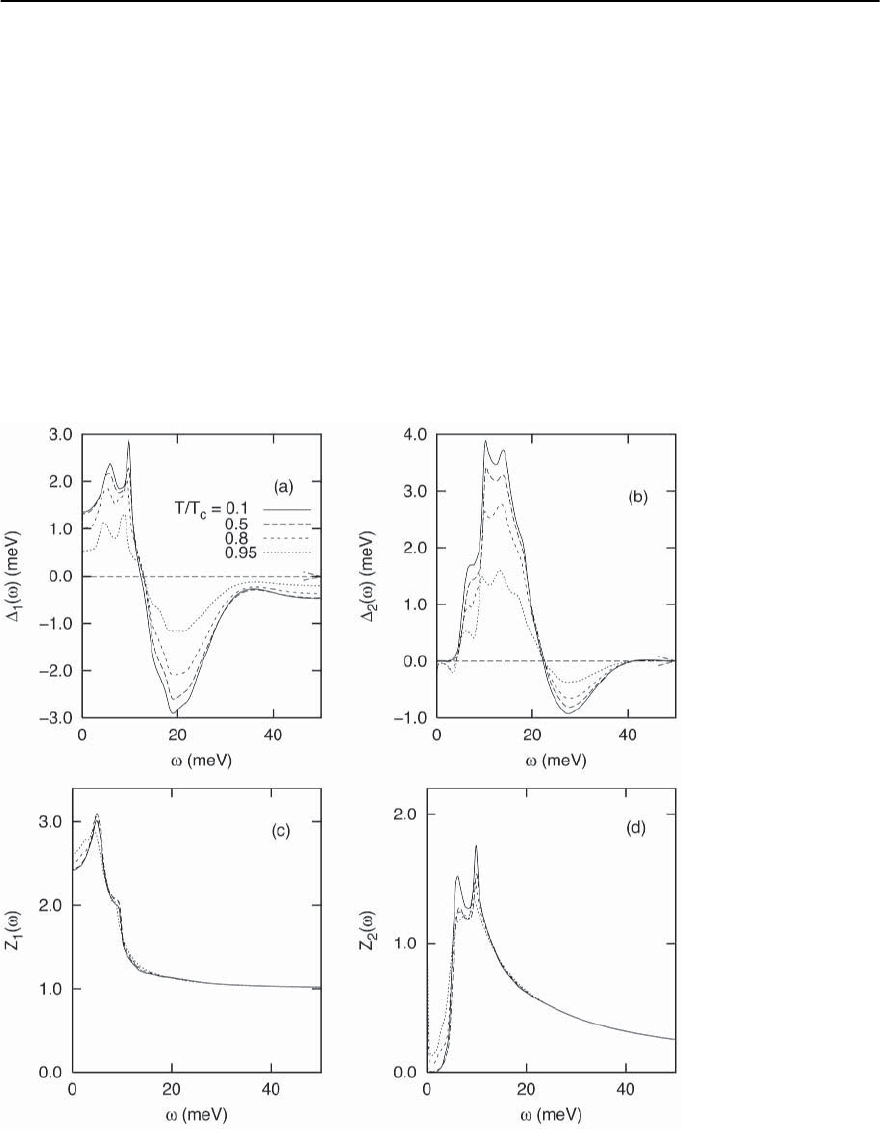
3 Electron–Phonon Superconductivity 115
Fig. 3.33a, along with the density of states at several
temperatures (Fig. 3.33b).
Within Eliashberg theory, the calculation of the
corresponding property is much more complicated.
First of all, a careful distinction between the gap or
pairing function (which is now a function of fre-
quency at any given temperature) and the energy
gap is required. The energy gap is defined through
Eq. (3.83). The gap function is, in general, a compli-
cated and complex functionof frequency,that results
from a solution of the Eliashberg equations. These,
in turn, can be solved either on the imaginary axis
(Eqs. (3.55) and (3.58) for the “standard” theory) or
the real axis (Eqs. (3.77) and (3.78)). Example solu-
tions for a real electron–phonon spectrum (Pb) are
shown in Fig. 3.34. The solutions on the imaginary
axis turn out to be real; on the real axis they are com-
plex.The corresponding densities of states are shown
in Fig. 3.36.
The low frequency behaviour of the various func-
tionsplottedisnotclearonthefiguresshown.A
careful analysis [171] leads to
Re(!)=c,
Im(!)=0,
ReZ(!)=d,
ImZ(!)=0.
(3.126)
at zero temperature, where c and d are constants,
whereas at any non-zero temperature, we obtain
Fig. 3.36. The (a)real
and (b)imaginaryparts
of the gap function (in
meV) on the real fre-
quency axis, for Pb,
for various tempera-
tures, as in the previous
figure. Note the consid-
erable structure present
on the real axis. Also
shown is the (c)real
and (d) imaginary part
of the renormalization
function, Z(!)vs.!

116 F. Marsiglio and J.P. Carbotte
Re(!) ∝ !
2
,
Im(!) ∝ !,
ReZ(!)=d(T),
ImZ(!) ∝ 1/!.
(3.127)
The latter result in particular implies that, strictly
speaking, at finite temperature there is always “gap-
less”superconductivity.However,as can be seen from
Fig.3.36,in reality the“finitetemperature”density of
states at zero energy is generally quite small (except
for very close to T
c
). The extent to which this is true
depends on the electron–phonon coupling strength;
as this increases the zero frequency density of states
can be a significant fractionof the normal state value
at temperatures near T
c
[173].
In the remaining subsections we wish to exam-
ine the dependence of the energy gap on coupling
strength. Since the electron–phonon interaction is
characterized by a spectral function, ˛
2
F(§),we first
must decide how to quantify the coupling strength
of a particular superconductor.Historicallythe mass
enhancement parameter, given by Eq. (3.21), has
played this role. However, depending on the mate-
rial, the direct Coulomb repulsion, characterized by
∗
(!
c
), where !
c
is some suitable cutoff frequency,
can offset the effect of . Another possible parame-
ter is the ratio of the critical temperature to an aver-
age phonon frequency, a quantity first advocated by
Geilikman and Kresin [234–237]. This approach was
further quantified by Mitrovi´cet al.[238].In this ref-
erence (see also [239]), the Allen–Dynes parameter
T
c
/!
ln
emerged naturally in the derivation of strong
coupling corrections, as an indicator of coupling
strength. A large number of superconducting prop-
erties were obtained in this way (see Refs. [10,240]
for derivationsandmore details),andsemi-empirical
fits were obtained based on accurate numerical solu-
tions. We discuss these further in the next section.
3.4.5 The Energy Gap:
Dependence on Coupling Strength T
c
=!
`n
As we have already emphasized, T
c
cannot be reli-
ably calculated at present.The first,perhaps simplest,
test for the accuracy of Eliashberg theory is then its
ability to properly obtain the gap ratio, 2
◦
/k
B
T
c
,
where,by
◦
,wemeanthezerotemperaturegapedge.
In[238] (seealso [10]),numerically calculatedresults
were compared to experimental tunneling results for
◦
, obtained for a variety of conventional elemental
and alloy superconductors.Thedeviations of the gap
ratio from the BCS universal result, 2
◦
/k
B
T
c
=3.53,
are up to 50 %; yet the level of experimental error is
about 5 % , with one notable exception (Nb
3
Sn). The
theoretical results are obtained from a solution of
the imaginary axis equations (Eqs. (3.55) and (3.58),
with the standard approximations of infinite band-
width and particle-hole symmetry), followed by an
analytical continuation to the real axis. To obtain the
gap edge, a Pad´e approximant suffices to get very
accurate results [160], as the more systematic con-
tinuation [163] verifies. In any event it is desirable
to have an analytic form for these corrections. The
result of Mitrovi´c et al. [238] is
2
◦
k
B
T
c
=3.53
1+12.5
T
c
!
ln
2
ln (
!
ln
2T
c
)
. (3.128)
In obtaining this result the spirit of the McMillan
equation was followed, and the coefficients 12.5and
2 were chosen from fits to the numerical data for a
large number of superconductors. These results are
plotted in Fig. 3.37. From this Figure it is clear that
Eq. (3.128) describes the overall trend very well. As
the electron–phonon interaction increases (i.e. be-
comes more retarded), the gap ratio increases to val-
ues exceeding 5.0.
Figure 3.37 illustrates that a simple analytic form
describes the trend of the gap ratio as a function of
T
c
/!
ln
rather well for a variety of conventional su-
perconductors. In each case electron–phonon spec-
tral functions were used, as obtained from tunnel-
ing data, or, in some cases, model calculations. On
occasion, one sometimes uses a phonon spectrum
obtained from inelastic neutron scattering, scaled to
give the measured critical temperature. This latter
process assumes that the electron–phonon coupling
is constant as a function of frequency (seen to be rea-
sonable in the case of Pb), and often assumes a value
of the Coulomb pseudopotential,
∗
(!
c
=6!
max
) ≈
0.1(!
max
is the maximum phonon frequency). Spe-
cific references to the sources of these spectra can be
found in Refs. [10,240].
