Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.

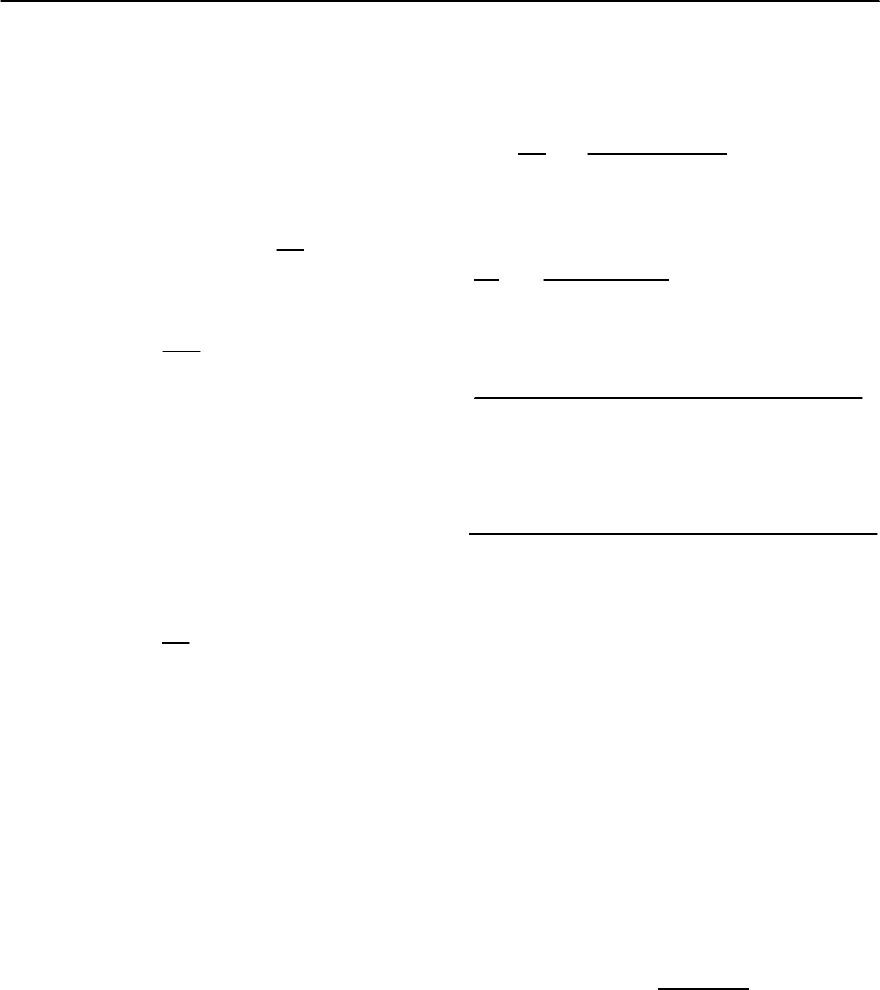
3 Electron–Phonon Superconductivity 87
T
c
= !
D
/2. (3.41)
It is clear that T
c
or the zero temperature variational
parameter depend on material properties such as
the phonon spectrum (!
D
), the electronic structure
(N()) and the electron–ion coupling strength (V).
However, it is possible to form various thermody-
namic ratios, which turn out to be independent of
material parameters. The obvious example from the
preceding equations is the ratio
2
k
B
T
c
.Inweakcou-
pling (most relevant for conventional superconduc-
tors), for example, we obtain
2
k
B
T
c
=3.53, (3.42)
a universal result, independent of the material in-
volved. Many other such ratios can be determined
within BCS theory,and the observed deviationsfrom
these universal values contributed to the need for an
improved formulation of BCS theory. For example,
the observed value of this ratio in superconducting
Pb was closer to 4.5,a resultthat is readily understood
with Eliashberg theory.It is worth noting that simply
extending BCS theory to the strong coupling limit
(see Eqs. (3.38) and (3.41) above) results again in a
universal constant,
2
k
B
T
c
= 4, which is the maximum
value attainable within BCS theory with a constant
interaction [108], and is still clearly too low.
Other aspects of BCS theory, particularly those
which prove to inadequately account for the super-
conducting properties of some materials (notably Pb
and Hg) will not be reviewed here. Instead, we will
makereference to the BCS limit as we encounter vari-
ous properties within the experimental or Eliashberg
context.
Eliashberg Equations
In most reviews and texts that derive the Eliashberg
equations, the starting point is the Nambu formal-
ism [2]. While this formalism simplifies the actual
derivation, it also provides a roadblock to further
understanding for the uninitiated.For this reason we
have followed the conceptually much more straight
forward approach (provided by Rickayzen [55], for
example) in the derivation outlined in the Appendix.
The result can be summarized by the following set of
equations:
£(k, i!
m
) ≡ (3.43)
1
Nˇ
k
,m
kk
(i!
m
− i!
m
)
N()
G(k
, i!
m
) ,
(k, i!
m
) ≡ (3.44)
1
Nˇ
k
,m
kk
(i!
m
− i!
m
)
N()
− V
kk
F(k
, i!
m
) ,
G(k, i!
m
) = (3.45)
G
−1
n
(−k, −i!
m
)
G
−1
n
(k, i!
m
)G
−1
n
(−k, −i!
m
)+(k, i!
m
)
¯
(k, i!
m
)
,
with
F(k, i!
m
) = (3.46)
(k, i!
m
)
G
−1
n
(k, i!
m
)G
−1
n
(−k, −i!
m
)+(−k, −i!
m
)
¯
(−k, −i!
m
)
G
−1
n
(k, i!
m
)=G
−1
◦
(k, i!
m
)−£(k, i !
m
). (3.47)
Another couple of equations identical to Eqs. (3.45)
and (3.46), except with
¯
and
¯
F instead of and F,
have been omitted; they indicate that some choice of
phase is possible,which will be important for Joseph-
son effects [109] but not for what will be considered
in the remainder of this chapter. Therefore, we use
¯
= .
Note, that G
−1
◦
(k, i!
m
) is the inverse of the
non-interacting Green function, in which Hartree–
Fock contributions from both the electron–ion and
electron–electron interactions are assumed to be
contained.
Following the standard practice we have used a
kernel given by
kk
(z) ≡
∞
0
2˛
2
kk
F( )
2
− z
2
d , (3.48)
where ˛
2
kk
F( ) is given by Eq. (3.16). Equations
(3.43)–(3.48) have been written in a fairly gen-
eral way; in this way they can be viewed as hav-
ing arisen from a microscopic Hamiltonian as in

88 F. Marsiglio and J.P. Carbotte
Eqs. (3.2)–(3.4) (although electron–electron interac-
tions have been included in the pairing channel only,
and not in the single electron self-energy), or, alter-
natively, from a treatment of real metals, where, as
mentioned earlier, the electron and phonon struc-
ture come from previous calculations and/or ex-
periments. These equations emphasize the electron–
ion interaction; attempts to explain superconductiv-
ity through the electron–electron interactions have
been proposed in the past, mainly through collec-
tive modes [110–117]; some of these attempts will
be treated elsewhere in this volume in the context of
high temperature superconductivity.
Assuming the electron and phonon structure is
given, Eqs. (3.43)–(3.48) must be solved for the two
functions, £(k, i!
m
)and(k, i!
m
). The procedure
is as follows: it is standard practice to separate the
self-energy, £(k, i!
m
),into its even and odd compo-
nents [12]:
i!
m
1−Z(k, i!
m
)
≡
1
2
£(k, i!
m
) (3.49)
− £(k, −i!
m
)
,
(k, i!
m
) ≡
1
2
£(k, i!
m
)
+ £(k, −i!
m
)
,
where Z and are both even functions of i!
m
(and,
as we’ve assumed all along, k). Then, Eq. (3.43) be-
comes two equations,
Z(k, i!
m
)=1+
1
Nˇ
k
,m
kk
(i!
m
− i!
m
)
N()
(3.50)
×
!
m
/!
m
Z(k
, i!
m
)
!
2
m
Z
2
(k
, i!
m
)+
k
− + (k
, i!
m
)
2
+
2
(k
, i!
m
)
,
(k, i!
m
)=−
1
Nˇ
k
,m
kk
(i!
m
− i!
m
)
N()
(3.51)
×
k
− + (k
, i!
m
)
!
2
m
Z
2
(k
, i!
m
)+
k
− + (k
, i!
m
)
2
+
2
(k
, i!
m
)
along with the gap equation (3.44):
(k, i!
m
)=
1
Nˇ
k
,m
kk
(i!
m
− i!
m
)
N()
− V
kk
(3.52)
×
(k
, i!
m
)
!
2
m
Z
2
(k
, i!
m
)+
k
− + (k
, i!
m
)
2
+
2
(k
, i!
m
)
.
These are supplemented with the electron num-
ber equation, which determines the chemical poten-
tial, :
n =
2
Nˇ
k
,m
G(k
, i!
m
)e
i!
m
0
+
, (3.53)
or
n =1−
2
Nˇ
(3.54)
×
k
,m
k
− + (k
, i!
m
)
!
2
m
Z
2
(k
, i!
m
)+
k
− + ((k
, i!
m
)
2
+
2
(k
, i!
m
)
.
These constitute general Eliashberg equations for
the electron–phonon interaction, in which electron–
electron interactionsenter explicitly only in the pair-
ing equation. Very complete calculations of these
functions (linearized, for the calculation of T
c
)were
carried out for Nb by Peter et al. [118], and for Pb by
Daams [119].
The more standard practice is to essentially con-
fine all electronic properties to the Fermi surface;
then only the anisotropy of the various functions
need be considered. Often these are simply aver-
aged over (due to impurities, for example), or the
anisotropy may be very weak and therefore ne-
glected.In this case Eqs.(3.50)–(3.54) can be written
Z
m
=1+T
m
(i!
m
− i!
m
) (3.55)
×
(!
m
/!
m
)Z
m
!
2
m
Z
2
m
+
2
m
A
0
(m
) ,
m
=−T
m
(i!
m
− i!
m
)A
1
(m
) ,(3.56)
m
= T
m
(i!
m
− i!
m
)−N()V
coul
(3.57)
×
m
!
2
m
Z
2
m
+
2
m
A
0
(m
) ,
n =1−2TN()
m
A
1
(m
) , (3.58)

3 Electron–Phonon Superconductivity 89
wherewehaveadoptedtheshorthandZ(i!
m
)=Z
m
,
etc, (z )andV
coul
represent appropriate Fermi sur-
face averages of the quantities involved, and the
functions A
0
(m
)andA
1
(m
) are given by integrals
over appropriate density of states, using the pre-
scription (3.19) to convert from Eqs. (3.50)–(3.54)
to Eqs. (3.55)–(3.58). If the electron density of states
is assumed to be constant, then, with the additional
approximation of infinite bandwidth, A
0
(m
) ≡ 1
(actually a cutoff, (!
c
− | !
m
|), is required in
Eq. (3.58)), and A
1
(m
) ≡ 0. This last result effec-
tively removes
m
(and Eqs. (3.56) and (3.58) ) from
further consideration. An earlier review by one of
us [10] covered the consequences of the remaining
two coupled equations in great detail.
All of the equations discussed so far have been
developed on the imaginary frequency axis. Because
practitioners in the field at the time were interested
in tunneling spectroscopy measurements [47], the
theory was first developed on the real frequency
axis [4,45]. The resulting equations are complicated,
even for numerical solution. It wasn’t until quite a
number of years later that numerical work returned
to the imaginary axis [120], where, for thermody-
namic properties, the numerical solution was very
efficient [121–124]. The difficulty, however, was that
imaginary axis solutions are not suitable for dynam-
ical properties. We will return to the interplay be-
tween imaginary and real frequency axis solutions
as we encounter them throughout the chapter.
The other complication we have mentioned is an
energy variation in the EDOS, as seems to exist in
some A15 compounds. If this energy dependence oc-
curs on a scale comparable to !
D
,thenN()can-
not be assumed to be constant, and cannot be taken
outside of the integrals in Eqs. (3.50)–(3.54). Such
EDOS energy dependence is thought to be respon-
sible for some of the anomalous properties seen
in A15 compounds — their magnetic susceptibility
and Knight shift [125], and the structural transfor-
mation from cubic to tetragonal [126–128]. Several
electronic bandstructurecalculations[129–132] also
findsharpstructurein N() at the Fermi level.An ac-
curate description of the superconducting state thus
requires a proper treatment of this structure. This
was first undertaken to understand T
c
by Horsch
and Rietschel [133] and independently by Nettel and
Thomas [134]. A more general approach to under-
standing the effect of energy dependence in N()on
T
c
was given by Lie and Carbotte [135], who for-
mulated the functional derivative ıT
c
/ıN(); they
found that only values of N()within5to10times
T
c
around the chemical potential have an apprecia-
ble effect on the value of T
c
. More specifically they
found that ıT
c
/ıN() is approximately a Lorentzian
with center at the chemical potential; the function
becomes negative only at energies | − |
>
∼
50T
c
.
Irradiation damage experiments illustrate some
of this dependency. For example, irradiation of
Mo
3
Ge causes an increase in T
c
[136]. Washing out
gap anisotropy with the irradiation cannot possibly
account foran increase in T
c
;instead,thisresultfinds
a natural explanation in the fact that the chemical po-
tential for Mo
3
Ge falls in a valley [137] of the EDOS,
and irradiation smears the EDOS, thus increasing
N(), and hence T
c
.
In what follows we will sketch some of the the-
ory behind this work; More details on the formula-
tion of Eliashberg theory with an energy dependent
N() can be found in the work of Pickett [138] and
Mitrovi´c and Carbotte [139], and references therein.
To treat the possible energy dependence in the
band structure EDOS one can return to Eqs. (3.43)–
(3.47). Beginning with the normal state, already an
important point is apparent: namely the Green func-
tion and self-energy must be solved self-consistently
when there is a significant energy dependence in the
bareEDOS.Forexample,inEq.(3.43),ifanisotropyin
theinteraction is neglected,thenthe resulting k
-sum
can be converted into a single integral over energy
with the integrand weighted by the EDOS N(
). In
the zero temperature limit, one obtains, on the real
axis,
£(! + iı)=
+∞
−∞
d!
˜
N(!
)
∞
0
d§˛
2
F(§) (3.59)
×
(!
)
! − !
− § + iı
+
(−!
)
! − !
+ § + iı
,
where the renormalized EDOS is defined by
˜
N(!)=
+∞
−∞
d
N()
N()
−
1
Im G(, ! + iı)
.
(3.60)
90 F. Marsiglio and J.P. Carbotte
In principle the interaction, though isotropic, could
in fact depend on energy; this leads naturally to the
electron-phonon spectral function
˛
2
F(,
, §)=
k,k
˛
2
k,k
F(§)ı( −
k
)ı(
−
k
)
N()N(
)
.
(3.61)
Usually the dependence on and
is not signifi-
cant so that often these energies are simply evaluated
at the Fermi energy, and the Eq. (3.59) results. The
reader is referred to the work of Mitrovi´candCar-
botte [140] for details concerning the effects of the
energy dependence in Eq.(3.61) on superconducting
properties.
Equations (3.59) and (3.60) must be solved self-
consistently. Solutions for a model bare density of
states N() (used to mimic the calculated bare EDOS
for Nb
3
Sn [129]) are given in [139,141]. The model
(dotted curve) along with the calculated renormal-
ized EDOS (solid curve) is shown in Fig.3.6 in an en-
ergy range near the Fermi energy.The model consists
of a triangular peak superposed on a constant back-
ground. The calculation uses an electron-phonon
spectral functionextracted from tunneling measure-
ments [142]. Note that the calculated renormalized
EDOS is sharper than the bare EDOS. Also, there are
Fig. 3.6. The renormalized EDOS (solid curv e)andthe
model bare EDOS (normalized to its value at the bare
chemical potential) (dotted curve) vs. energy near the
chemical potential (! =0).Thesolid circle indicates the
(bare) chemical potential corresponding to the bare EDOS
at zero temperature. The actual chemical potential for the
interacting system has been defined to be zero.Reproduced
from [139]
slight modulations in the ±20−30 meV regionwhich
correspond to phonon structure. Finally, note that
the bare EDOS does not have particle-hole symme-
try; this results in a shift in the chemical potential
(from the filled dot, which corresponds to the chem-
ical potential for a given electron density in the bare
EDOS, to zero, which is the chemical potential cor-
responding to the renormalized EDOS). The shift is
given by the value of the real part of £(! +iı)atzero
frequency.
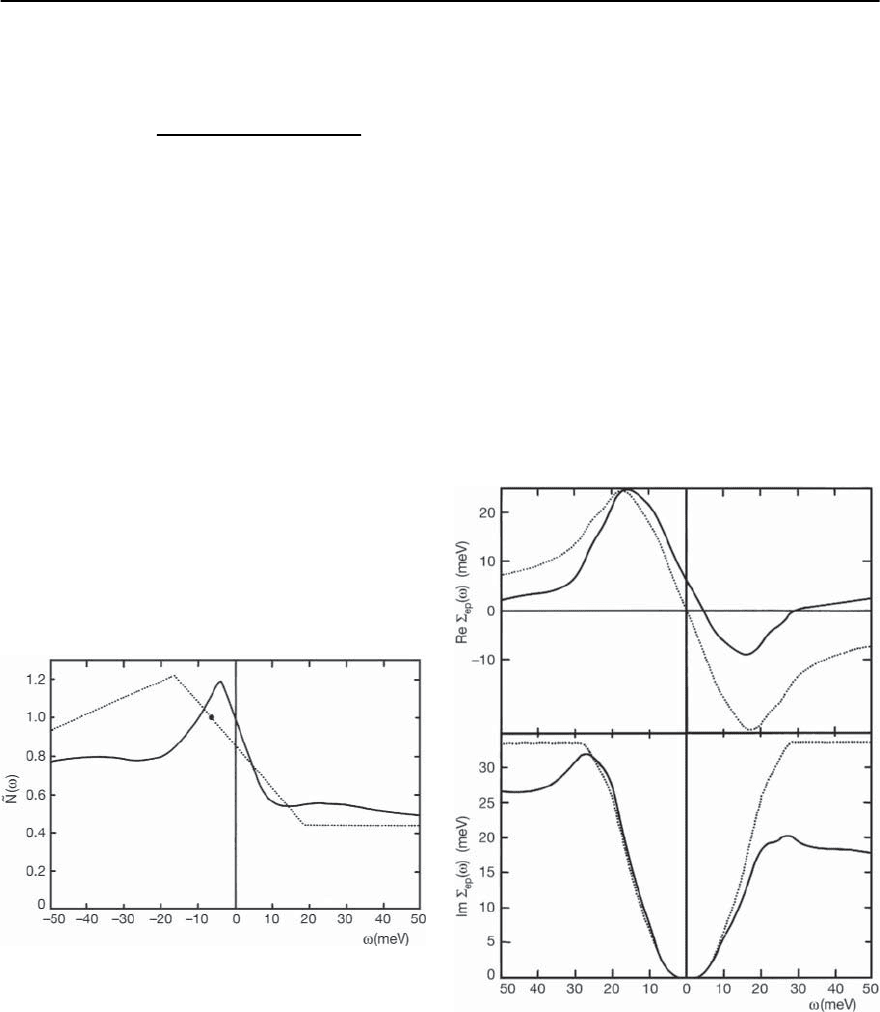
More detailed structure is visible in the self-
energy. The real and imaginary parts of the self-
energy are shown in the top and bottom frames of
Fig.3.7,respectively. The solid curves result from the
full calculation, consistent with Fig. 3.6. The dotted
curves are obtained with a constant EDOS with value
equal to that of the bare EDOS at the chemical po-
tential. These curves have electron-hole symmetry,
Fig. 3.7. The real (top frame) and imaginary (bottom f rame)
parts of the electron–phonon self-energy computed for the
model EDOS in Fig. 3.6 (solid curve) and for a constant
EDOS (dotted line) with value equal to that at the chemical
potential.Reproduced from [139]
3 Electron–Phonon Superconductivity 91
while the solid curves obviously do not. For exam-
ple, in the real part of the self-energy the maximum
value at negative frequency is clearly much higher in
magnitude than the minimum value at positive fre-
quency. Also note that Re £(! + iı) for ! =0isno
longer zero. For this case it has a significant value of
6.43 meV. Another noteworthy result is that
˜
N(! =0)=
−
1
Im
+∞
−∞
d
N()/N()
− −Re£(0 + iı)+iı
= N( =−Re£(0 + iı))/N(). (3.62)
ThevalueoftherenormalizedEDOSatthechemi-
cal potential remains equal to unity.This means that
the chemical potential is shifted by an amount equal
to Re £(0 + i ı) with respect to the “bare” chemical
potential ().
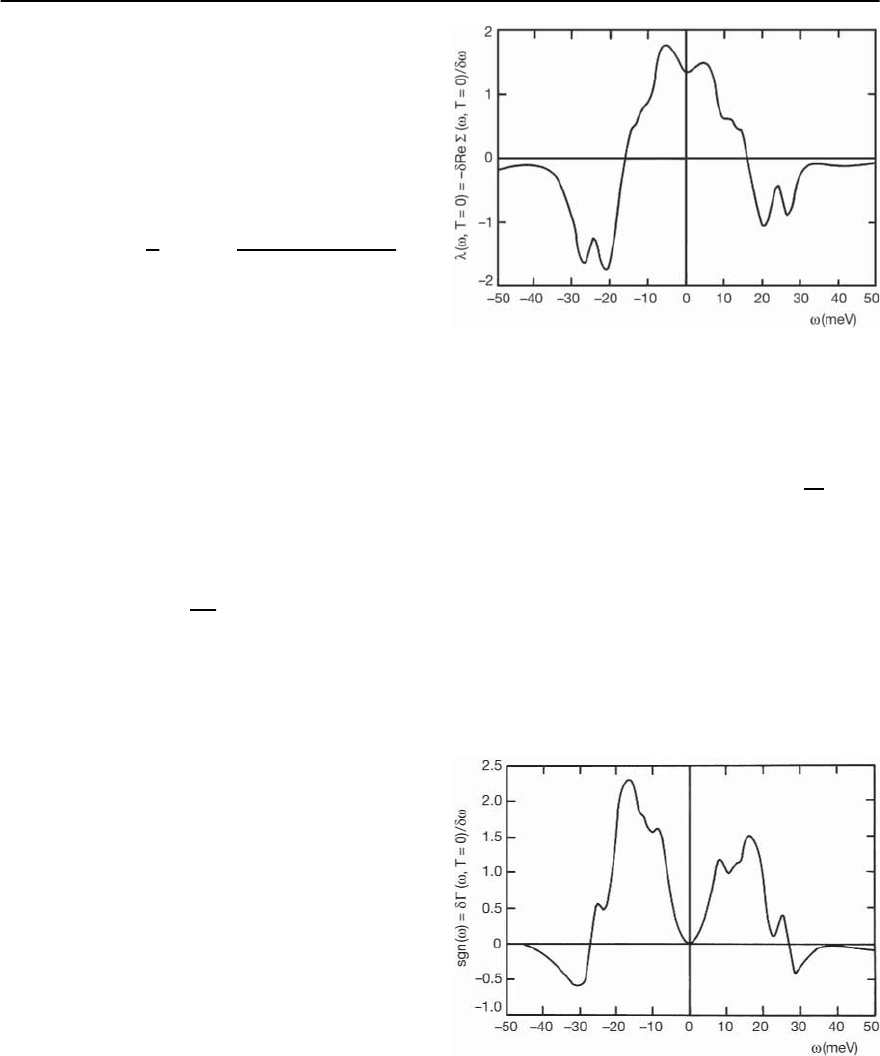
As in the case with a constant bare EDOS, here we
can define a frequency dependent mass renormal-
ization parameter (!) and a damping factor (!)
through the relations
(!) ≡ −
@
@!
Re£(! + iı) (3.63)
and
(!) ≡|Im£(! + iı)|. (3.64)
In Fig. 3.8 we show (!)vs.! forthe parameters dis-
cussed above. Note the lack of particle-hole symme-
try. According to the prescription (3.63) (0) = 1.33,
which is 22% smaller than that given by the stan-
dard definition, Eq. (3.21) (which gives 1.7 for the
Nb
3
Sn spectrum). For a constant bare EDOS these
two definitions would agree. One can also derive an
expression for (!)(atT =0):
(!)=
|!|
0
d!
×
(!)
˜
N(!
)+(−!)
˜
N(−!
)
× ˛
2
F(|!| − !
),
(3.65)
which reduces to the “standard” formula when
˜
N(!) = 1. Then the frequency derivative of the
Fig. 3.8. The electron–phonon renormalization parameter
as a function of frequency near the chemical potential, at
zero temperature. Reproduced from [139]
imaginary part of the self-energy gives ˛
2
F(!)di-
rectly. This is no longer true for a non-constant bare
EDOS, as shown in Fig. 3.9 where we plot
d
d!
| (!)|
vs.!.Once again the resultis asymmetric,anddiffers
considerably from the actual ˛
2
F(!), particularly
for |!|
>
∼
20 meV, where the derivative is negative.
More details are provided in [139]. Results concern-
ing far-infrared spectroscopy, obtained by Mitrovi´c
and Perkowitz [143]for V
3
Si thin films in the normal
state, will be discussed in a later section following
the “standard” description of far-infrared spectro-
scopy.
Fig. 3.9. The derivative of the electron scattering rate with
respect to frequency as a function of frequency at zero
temperature. Reproduced from [139]
92 F. Marsiglio and J.P. Carbotte
3.3 The Phonons
3.3.1 Neutron Scattering
When dealing with model Hamiltonians,the phonon
dispersionrelations(beforeinteractionwith theelec-
trons) are generally given, and simple: they are Ein-
stein modes, or Debye-like modes, for example. A
notable exception is the case where the model con-
tains anharmonic forces,in which case eventhe“non-
interacting”phonon spectrum is unknown.
In the case of real solids, and in particular metals,
the situation is much worse. In this case the elec-
trons cannot be ignored, though they can be treated
in the Born–Oppenheimer approximation.Nonethe-
less the results require parametrization (with input
from other experiments) and are generally not reli-
able. Pseudopotential methods [144,145] can be ap-
plied to this problem, again, with limited success. In
contrast, the spectacular success of inelastic neutron
scattering techniques [87,88] to simply measure the
phonon dispersion curves in real metals effectively
eliminates the need to calculate them quantitatively.
Various qualitative effects, like the impact of elec-
tronic screening on the long wavelength ionic plasma
mode [146], as well as the existence of Kohn anoma-
lies [147],all due to the presence of electrons,are un-
derstood theoretically. For detailed results, however,
Born–von Karman fits to high symmetry phonon
dispersions suffice for an excellent description of
the low temperature phonon properties. At temper-
atures of order 10 K, the phonons in most conven-
tional superconductors are completely determined,
and no longer changing with temperature. Hence,
as far as understanding (low temperature) super-
conductivity is concerned, these higher temperature
measurements are sufficient.
The measured dispersion curves, !
q
(again,
branch indices are suppressed), are summarized in
the frequency distribution
F( )=
1
N
q
ı( − !
q
), (3.66)
where N is the number of ions in the system, and q is
a wavevector which ranges over the entire First Bril-
louin Zone(FBZ),(andimplicitly containsthe branch
index). It should be stressed that this procedure is
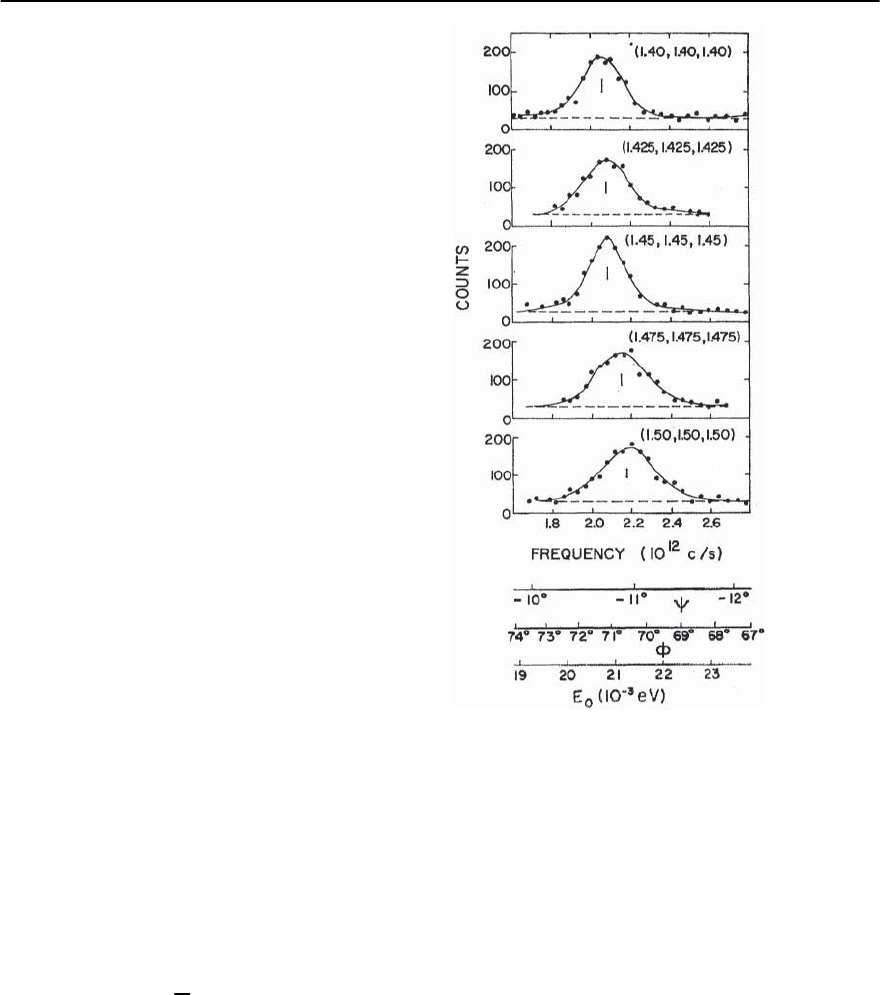
Fig. 3.10. Asetof“constantq” scans in Pb taken at various
points along thediagonal in the Brillouin zone.Reproduced
from [87]
an idealization; in actual fact a set of “constant q”
scans are performed (usually along high symmetry
directions).A typical result [87] is shown in Fig.3.10
for Pb, for a set of wavevectors along the diagonal in
reciprocal space. Note that the neutron counts tend
to form a peak as a function of energy transfer (to
the neutron), . In general these peaks have a fi-
nite width, i.e. broader than the spectrometer reso-
lution; these are due to a variety of effects, for ex-
ample, anharmonic effects. Nonetheless, because the
peaks are relatively sharp compared to the centroid
energy, (i.e. the phonon inverse lifetimes are small
compared to their energies), these data are usually
presented in the form of Fig. 3.11, as a set of disper-

3 Electron–Phonon Superconductivity 93
Fig. 3.11. The dispersion curves for Pb
at 100 K, as a function of momen-
tum along various high symmetry di-
rections. Reproduced from [87]
sion curves. Figure 3.11 does obscure, however, the
lifetimesof thevarious phonons,andhence the valid-
ity of Eq. (3.66), where infinitely long-lived phonons
are assumed throughout the Brillouin zone, is called
into question.
Nonetheless, for most of the Brillouin zone the
approximation of infinitely long-lived excitations is
a good one (hence, the name, phonon), and so the
spectrum of excitations can be constructed accord-
ing to Eq. (3.66). Such a procedure relies on coherent
neutron scattering.An alternative is to use incoherent
neutron scattering, whereby one measures the spec-
trum more or less directly. This latter procedure has
advantages over the former, but also includes multi-
phonon scattering processes, and for non-elemental
materials, weighs the contribution from each ele-
ment differently, according to their varying scatter-
ing lengths. The result is often denoted the “general-
ized density of states” (GDOS). A comparison for a
Thallium-Lead alloy is shown in Fig. 3.12 [148,149].
Also shown is the result from tunneling, to be dis-
cussed in the next subsection. There is clearly good
agreement between the various methods. Amongst
the two neutron scattering techniques, inelastic co-
herent neutron scattering produces the sharpest fea-
tures, but requires a model (i.e. a Born–von Karman
fit) to extract the spectrum F( ) from the dispersion
curves measured along high symmetry directions.
3.3.2 The Eliashberg Function, ˛
2
F(): Calculations
First-principle calculations of the electron–phonon
spectral function, ˛
2
F( ) require a knowledge of the
electronic wave functions,thephonon spectrum,and
the electron–phonon matrix elements between two
single–electron Bloch states. A fairly comprehensive
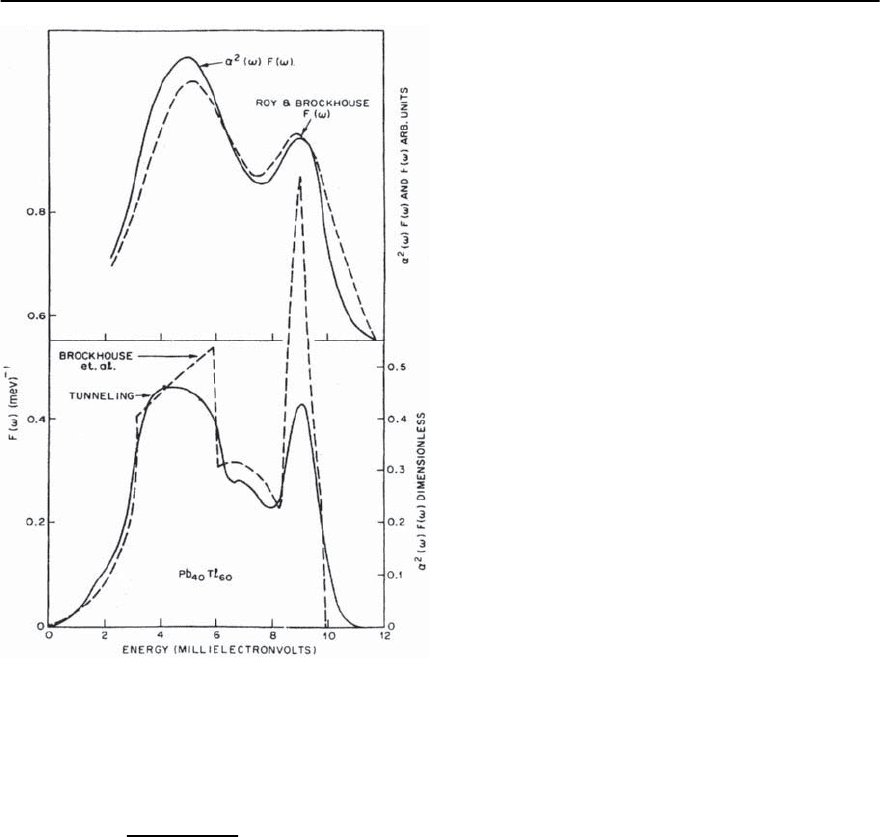
94 F. Marsiglio and J.P. Carbotte
Fig. 3.12. The electron–phonon spectral function ˛
2
F(!)
(solid curve)forPb
.40
Tl
.60
determined from tunneling ex-
periments and convoluted by instrument resolution of
the neutron spectrometer compared with the neutron re-
sults for the phonon frequency distribution F(!)(dashed
curve) measured by incoherent inelastic neutron scatter-
ing [149] (upper f rame). The lower frame shows the tun-
neling results (solid curve) compared with the phonon
frequency distribution (dashed curve) determined from a
BornvonKarmananalysisofthephonondispersioncurves
in Pb
.4
Tl
.6
[148]
review is given in [86]. For our purposes, we note
that, since the phonon spectrum will come from ex-
periment, Eq. (3.16) requires calculation of g
k,k
.It
is [10,86]
g
k,k
j
= <
k
|
j
(k − k
) ·∇V |
k
>
×
2M!
j
(k − k
)
1/2
,
(3.67)
where,for this equation we haveincluded the phonon
branch index j explicitly. The Bloch state is denoted
|
k
>,and
j
(k) is the polarization vector for the
(jk)th phonon mode.The crystal potential is denoted
V, and as one might expect, the electron–phonon
coupling depends on its gradient.
Tomlinson and Carbotte[150] used pseudopoten-
tial methods [151,152] to compute g
k,k
j
and, from
Eq. (3.16), ˛
2
F( ), for Pb. The phonons were taken
from experiment [87,88,153,154] through Born–von
K´arm´an fits. The result is plotted in Fig. 3.13, along
with results from tunneling experiments (to be de-
scribed below). The agreement is qualitatively very
good;thisprovidesverystrongconfirmationofthe
electron–phonon mechanism of superconductivity.
Further details of more modern calculations of
electron–phonon coupling constants can be found
in, for example, Refs. [74] and [75] and references
therein. Their reliability appears to remain an is-
sue, both with the high temperature cuprates, and
perhaps less so with the fulleride and more con-
ventional superconductors. The spirit of these cal-
culations is somewhat different than the older ones,
in that coupling constants are extracted from the
phonon linewidths, where it is assumed that the
phonon broadening is entirely due to the electron–
ion interaction (and not, say, anharmonic effects).
Allen [155, 156] derived a formula (Fermi’s Golden
Rule) for the inverse lifetime,
q
( ),of a phonon with
momentum (and branch index) q:
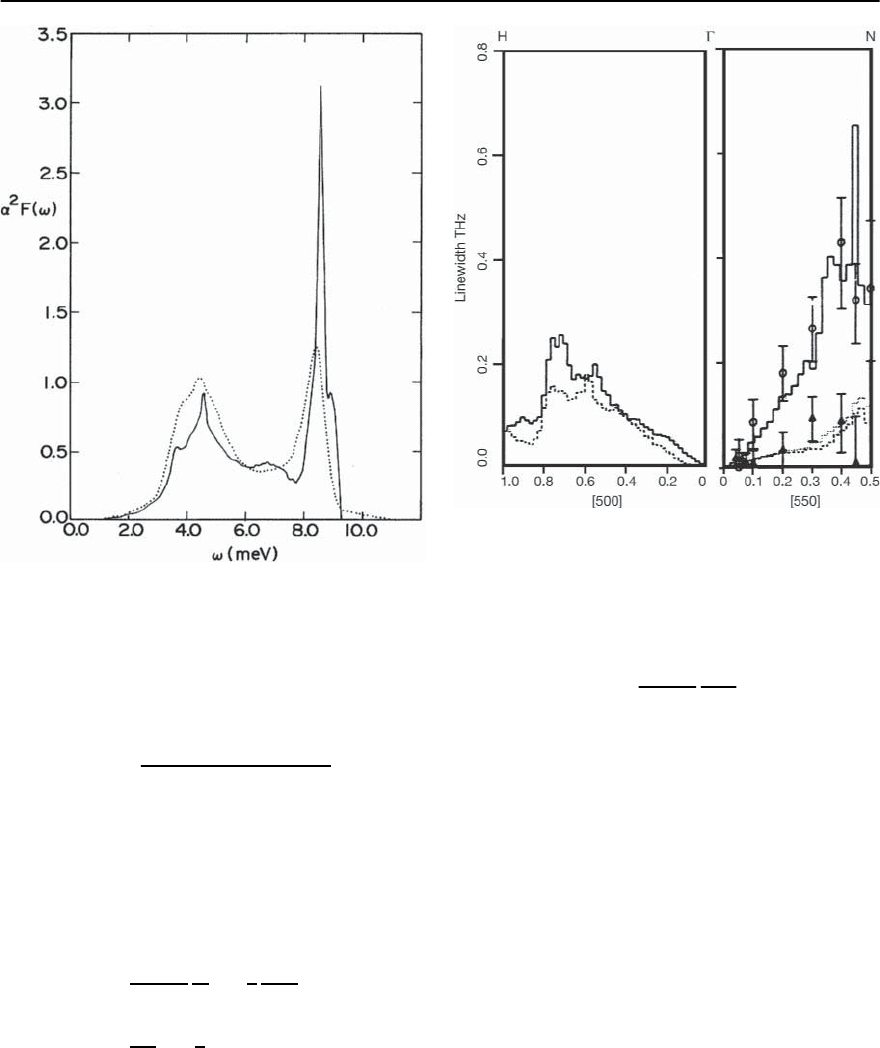
3 Electron–Phonon Superconductivity 95
Fig. 3.13. The electron–phonon spectral function ˛
2
F(!)
measured in tunneling experiments (dotted curve)com-
pared with that which is calculated from first principles
(solid curve) [150]
q
=2!
q
k
|g
k,k+q
|
2
×
f (
k+q
− )−f (
k
− )
!
q
(3.68)
×ı(
k+q
+ !
q
−
k
) ,
where again we have suppressed both phonon
branch indices and electron band labels. Using this
equation, in the approximation that the expres-
sion
f (
k+q
− )−f (
k
− )
/(!
q
)isreplacedby
ı(
k
− ) makes it resemble Eq.(3.17), one can write
˛
2
F( )=
1
N()
1
N
q
1
2
q
!
q
ı( − !
q
)
=
1
3N
q
1
2
!
q
q
ı( − !
q
) , (3.69)
where the second line serves to define a q-dependent
coupling parameter:
Fig. 3.14. A histogram of phonon linewidths in Nb. The
linewidths represent the full width at half-maximum for
both longitudinal modes (solid) and transverse modes
(dashed and do tted). The circles and triangles are from
experiment. Reproduced from [157]
q
≡
3
N()
q
!
2
q
. (3.70)
It is through these relations that coupling parameters
are often determined.
Butler et al. [157, 158] have made extensive cal-
culations of electron-phonon linewidths in Nb. Re-
sults of their calculated phonon lifetimes, based
on extended band structure calculations, are pre-
sented in Fig.3.14 for two high symmetry directions,
[, 0, 0] and [, , 0] for transverse (dashed and dot-
ted curves) and longitudinal (solid curve) branches.
A comparison with experimental results is also given.
The reader is referred to their papers for details. The
electron-phonon spectral density ˛
2
F( ) obtained
in this way through Eq. (3.69) is shown in Fig. 3.15
(histogram), where it is compared with an early ex-
perimental spectral function extracted from tunnel-
ing inversion by Robinson and Rowell [159] (solid
curve).
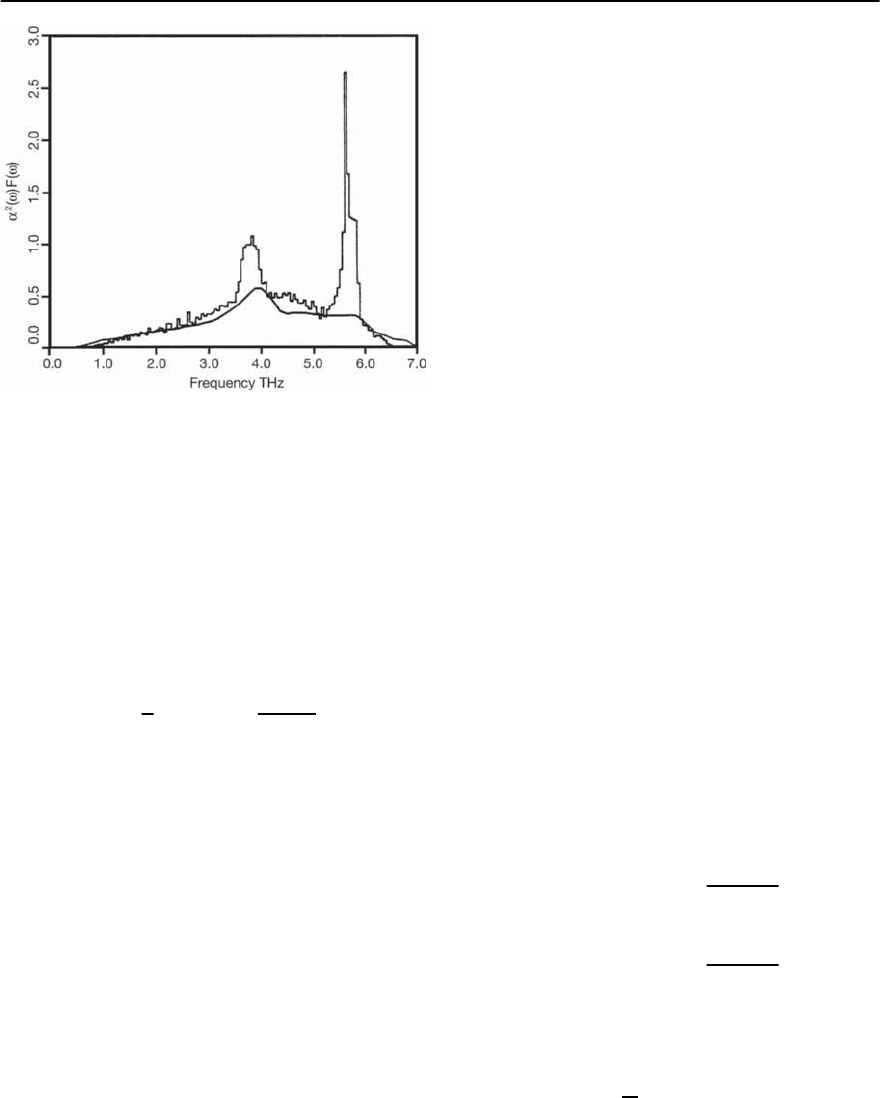
96 F. Marsiglio and J.P. Carbotte
Fig. 3.15. Calculated (histogram) and experimental (solid
curve) electron–phonon spectral function, ˛
2
F(§)forNb.
Reproduced from [157]
It is worth noting at this point that several
moments of the function ˛
2
F( )haveplayedan
important role in characterizing retardation (and
strong coupling) effects in superconductivity. Fore-
most amongst these is the mass enhancement pa-
rameter, , already defined in Eq. (3.21); in addition,
the characteristic phonon frequency, !
ln
is given by
!
ln
≡ exp
⎡
⎣
2
∞
0
d ln ( )
˛
2
F( )
⎤
⎦
. (3.71)
Further discussion of these calculations can be found
in Refs. [10,86].
3.3.3 Extraction from Experiment
Experiments which probe dynamical properties do
so as a function of frequency, which is a real quan-
tity.However,the Eliashberg equations as formulated
in the previous section are written on the imaginary
frequency axis. To extract information from these
equations relevant to spectroscopic experiments,one
must analytically continue these equations to the real
frequency axis. Mathematically speaking, this is not
a unique procedure; one can often imagine several
functions whose values on the imaginary axis are
equal, and yet differ elsewhere in the complex plane
(and in particular on the real axis). For example,
replacing unity by − exp (ˇi !
m
), in any number of
places in the equations does not affect the imaginary
axis equations, or their solutions, and yet on the real
axis the corresponding number of factors − exp (ˇ!)
will appear.
Physically speaking, however, the Green functions
involved have to satisfy certain conditions; comply-
ing with these conditions determines the function
uniquely [92]. This allows a unique determination of
theanalytic continuation oftheEliashbergequations
on the real axis. This procedure will be discussed in
the following subsection, followed by subsections on
experimental spectroscopies, and how they can be
used to extract the Eliashberg function, ˛
2
F( ).
The Real-Axis Eliashberg Equations
We begin with Eqs.(3.43)–(3.47).To analytically con-
tinue Eqs.(3.46)–(3.47) is trivial;one simply replaces
the imaginary frequency i!
m
wherever it appears
with ! + iı.Theiı remains to remind us that we are
analytically continuing the function to just above the
real axis; it is important to specify thissincethere isa
discontinuity in the Green function as one crosses the
real axis.A simple replacement of i!
m
with ! + iı in
Eqs. (3.43) and (3.45) (leaving the summations over
m
) would in general be incorrect. The correct proce-
dure is to first perform the Matsubara sum, and then
make the replacement. To perform the Matsubara
sum, however, one has to introduce the spectral rep-
resentation for the Green functions, G and F.These
are given by
G(k, i!
m
)=
∞
−∞
d!
A(k, !)
i!
m
− !
, (3.72)
F(k, i!
m
)=
∞
−∞
d!
C(k, !)
i!
m
− !
, (3.73)
where A(k, !) is given by Eq. (3.27) and C(k, !)is
givenbyasimilarrelation:
C(k, !) ≡ −
1
ImF(k, ! + iı). (3.74)
