Беляев В.М., Миронов В.М. Конструирование и расчет элементов оборудования отрасли. Часть 1: Тонкостенные сосуды и аппараты химических производств
Подождите немного. Документ загружается.

61
.;
4
1
;
2
;ctg
1
1
2
2
2
MKpR
k
M
pR
T
k
pR
U μ=
μ−
=
μ
=
⎟
⎠
⎞
⎜
⎝
⎛
ϕ
μ−
−=
Затем проверяются условия прочности, как минимум, для двух сечений при
kx=0 и при kx=π/4.
3.4. Цилиндрическая обечайка и днище в виде сферического сегмента,
нагруженные внутренним газовым давлением р
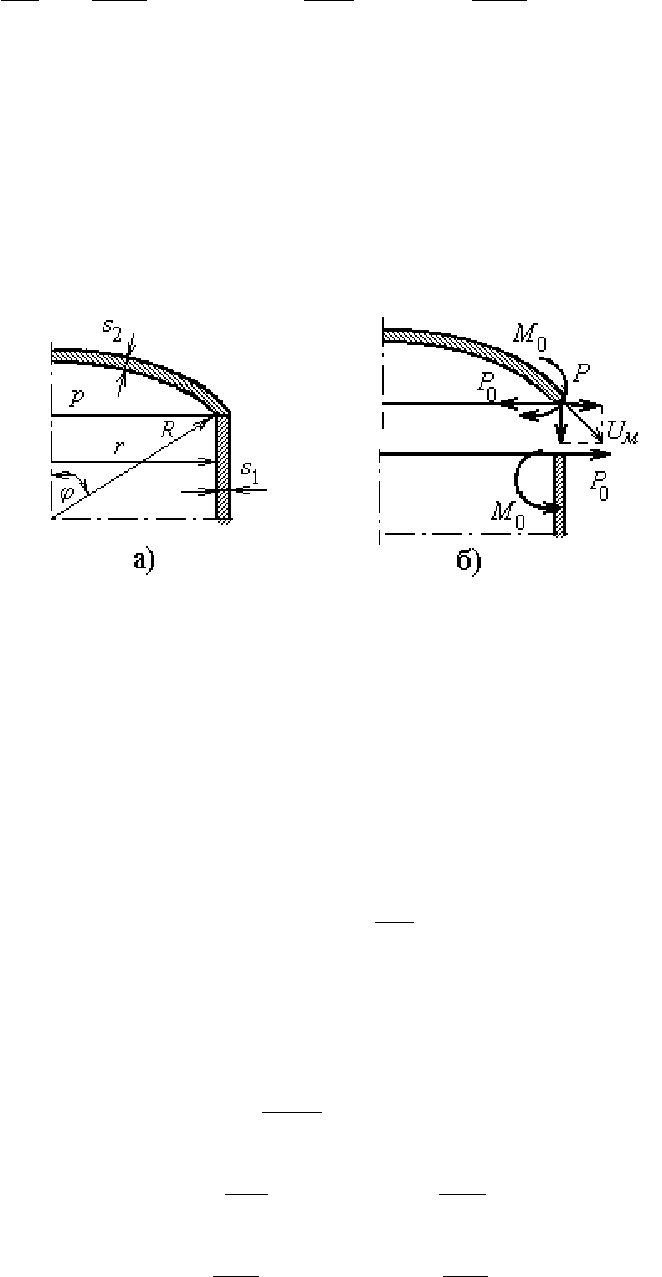
Схема нагружения и эквивалентная схема представлены на рис.3.10.
Рис. 3.10. К примеру 3.4
а – схема нагружения; б – эквивалентная схема
Введем обозначения:
s
1
и r – толщина стенки и радиус цилиндрической обечайки;
s
2
и R – толщина стенки и радиус сферического сегмента;
f=s
2
/s
1
– отношение толщин стенки крышки и стенки корпуса.
Распорная сила, приложенная к краю крышки,
.cos
2
cos ϕ=ϕ=
pR
UP
м
Радиальные и угловые перемещения краев соединяемых частей под действи-
ем давления p, краевых сил Р
0
и моментов М
0
будут равны:
а) для цилиндрической обечайки
;0;
2
2
ц
вн
2
1
ц
вн
=θ
μ
−
−=Δ pr
Es
;
2
;
2
2
0
1
2
ц2
0
1
ц
rP
Es
k
rP
Es
k
PoPo
=θ−=Δ
;
4
;
2
2
0
1
3
ц2
0
1
2
ц
rM
Es
k
rM
Es
k
MoMo
=θ−=Δ
б) для сферического сегмента
62
;0;sin
2
1
c
вн
2
2
c
вн
=θϕ
μ
−
−=Δ pR
Es
;sin)(
2
;sin)(
2
0
2
2
1
c
)(
2
0
2
1
c
)(
ϕ−=θϕ−=Δ
−−
PP
Es
k
RPP
Es
k
PPoPPo
.
4
;sin
2
0
2
3
1
c
0
2
2
1
c
M
ERs
k
M
Es
k
MoMo
−=θϕ−=Δ
Значения k и k
1
для цилиндра и сферы соответственно равны
.
)1(3
;
1(3
4
2
2
22
1
1
4
2
s
R
k
rs
k
μ−
=
μ−
=
Составим уравнение совместности деформации
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
−ϕ−=+
ϕ−ϕ−−
−ϕ
μ−
−=−−
μ−
−
.
4
sin)(
2
42
;sin
2
sin)(
2
sin
2
122
2
2
0
2
3
1
0
2
2
1
2
0
1
3
2
0
1
2
0
2
2
1
2
0
2
1
2
2
2
0
1
2
0
1
2
1
M
ERs
k
PP
Es
k
rM
Es
k
rP
Es
k
M
Es
k
RPP
Es
k
pR
Es
rM
Es
k
rP
Es
k
pr
Es
Поскольку
ϕ
=
sin
r
R
, а s
2
=f⋅s
1
, то k
1
можно представить в виде
.
sin
sin
1(3
)1(3
1
4
2
4
2
2
22
1
ϕ
=
ϕ
⋅μ−=
μ−
=
f
kr
fs
kr
s
R
k
После замены коэффициентов затухания k
1
на k получим
⎪
⎪
⎩
⎪
⎪
⎨
⎧
ϕ
−−=+
−−
ϕ
+
ϕ
μ−
−=−−
μ−
−
.
sin
2
)(
1
2
;
2
)(
sin2
sin2
1
22
2
2
00
2
00
0
2
2
1
00
2
0
M
ff
k
PP
f
kMP
M
f
k
PP
ff
k
p
f
MkkPp
В случае s
1
= s
2
= s, f=1 получим
⎪
⎪
⎩
⎪
⎪
⎨
⎧
ϕ
−−=+
−−ϕ+
ϕ
μ−
−=−−
μ−
−
.
sin
2
2
;2)(sin2
sin2
1
22
2
2
0000
0
2
00
2
0
M
k
PPkMP
MkPPkpMkkPp
При решении любой из указанных систем уравнений определяются
краевые силы Р
0
и моменты М
0
и соответствующие им напряжения.
Для сферических крышек и днищ влияние распорных сил на краевые
силы и моменты очень велико и оно увеличивается с уменьшением угла ϕ.

63
Напряжения в месте соединения обечайки и крышки получаются очень
большими, при этом краевые меридиональные напряжения намного превы-
шают мембранные. Поэтому применение неотбортованных сферических
днищ допускается только в аппаратах, работающих при давлениях не выше
0,07 МПа.
3.5. Цилиндрическая обечайка, соединенная с плоским
днищем и нагруженная давлением р
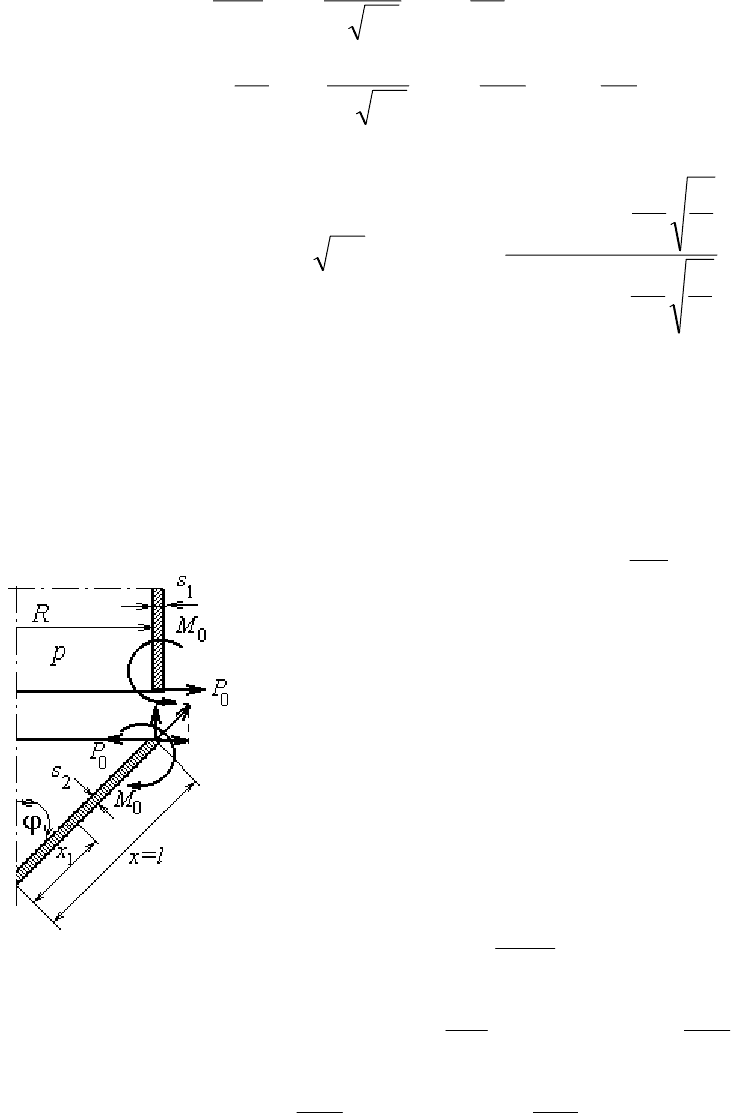
Схема нагружения и эквивалентная схема представлены на рис.3.11.
Рис. 3.11. К примеру 3.5
а – схема нагружения; б = эквивалентная схема
Линейные и угловые деформации:
а) для плоского днища
;
)1(8
1
;0
3д
вн
д
вн
pr
D μ+
−=θ=Δ
;0;0
1
д
0
2
д
=θ≈
μ
−
−=Δ
PoPo
rP
Es
,
)1(
1
;0
2
0
дд
rM
D
MoMo
μ−
=θ≈Δ
где D – цилиндрическая жесткость пластинки;
;
)1(12
2
3
2
μ−
=
Es
D
б) для цилиндрической обечайки
;0;
2
2
ц
вн
2
1
ц
вн
=θ
μ
−
=Δ pr
Es
;
2
;
2
2
0
1
2
ц2
0
1
ц
rP
Es
k
rP
Es
k
PoPo
−=θ−=Δ
.
4
;
2
2
0
1
3
ц2
0
1
2
ц
rM
Es
k
rM
Es
k
MoMo
=θ=Δ
Уравнения совместности деформации –
64
⎪
⎩
⎪
⎨
⎧
θ+θ=θ+θ
Δ=Δ+Δ+Δ
.
;
дд
вн
цц
ццц
вн
MoMoPo
MoPo
Принимая для стали μ=0,3 и подсчитывая значения k и D, получим
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−=+−
=+−
.
4,805,148,83,3
;0
3,357,285,0
0
3
2
2
3
2
0
1
2
1
0
2
1
0
2
1
0
11
1
M
s
pr
s
M
rss
P
s
M
s
rP
rss
pr
s
После решения системы имеем
.
31,356,6
85,082,0
;33,0
2
11
3
2
11
3
2
0100
pr
s
r
rs
s
s
r
rs
s
MrspkMP
+
+
=+=
Далее определяются краевые силы и моменты N, U, T, M и K как для
цилиндрической обечайки, так и для круглой плоской крышки.
3.6. Цилиндрическая обечайка,
соединенная с коническим днищем и нагруженная давлением р
Эквивалентная схема представлена на рис.3.12. Распорная сила равна
.sin
2
sin ϕ−=ϕ−=
pR
UP
Уравнение совместности деформации имеет
вид
⎪
⎩
⎪
⎨
⎧
θ+θ+θ=θ+θ+θ
Δ+Δ+Δ=Δ+Δ+Δ
−−
−−
.
;
кк
)(
к
вн
цц
)(
ц
вн
кк
)(
к
вн
цц
)(
ц
вн
MoPPoMoPPo
MoPPoMoPPo
Радиальные и угловые деформации под дейст-
вием внутреннего давления р, распорных сил Р,
краевых сил Р
0
и моментов М
0
будут равны:
а) для цилиндрической обечайки
;0;
2
2
ц
вн
2
1
ц
вн
=θ
μ
−
=Δ pR
Es
;
2
;
2
2
0
1
2
ц2
0
1
ц
RP
Es
k
RP
Es
k
PoPo
−=θ−=Δ
;
4
;
2
2
0
1
3
ц2
0
1
2
ц
RM
Es
k
RM
Es
k
MoMo
=θ=Δ
Рис. 3.12

65
б) для края конического днища, которое у вершины считается замкну-
тым, т.е. х
1
=0 и х=l
;
2
tg3
);2(
2
tgsin
2
2
к
вн
2
2
к
вн
Es
px
Es
px ϕ
=θμ−
ϕϕ
=Δ
;)(
)1(32
;)(
td
)1(32
0
2
2
к
)(
2
0
4
2
к
)(
RPP
Es
RPP
slsE
PPoPPo
−
μ−
=θ−
ϕ
μ−
=Δ
−−
;
cos
2
2
2
3
4
)
2
1(34
0
к
;
0
2
2
4
)
2
1(32
к
ϕ
μ−
=θ
μ−
=Δ
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
s
R
Es
M
Mo
RM
Es
Mo
).(
tg
)1(32
4
2
1
xl
s
k −
ϕ
μ−
=
Угловую деформацию можно выразить и так:
[
]
.
tg
)1(34
2
3
4
2
0
к
s
l
Es
M
Mo
ϕ
μ−
=θ
Подставляя значения линейных и угловых перемещений в уравнение
совместности деформаций и решая систему, получим значения краевых сил
Р
0
и моментов М
0
. Далее определяются краевые силы и моменты N, U, T, M и
K как для цилиндрической обечайки, так и для конического днища.
4. РАСЧЕ Т ТОНКИХ ПЛАСТИН
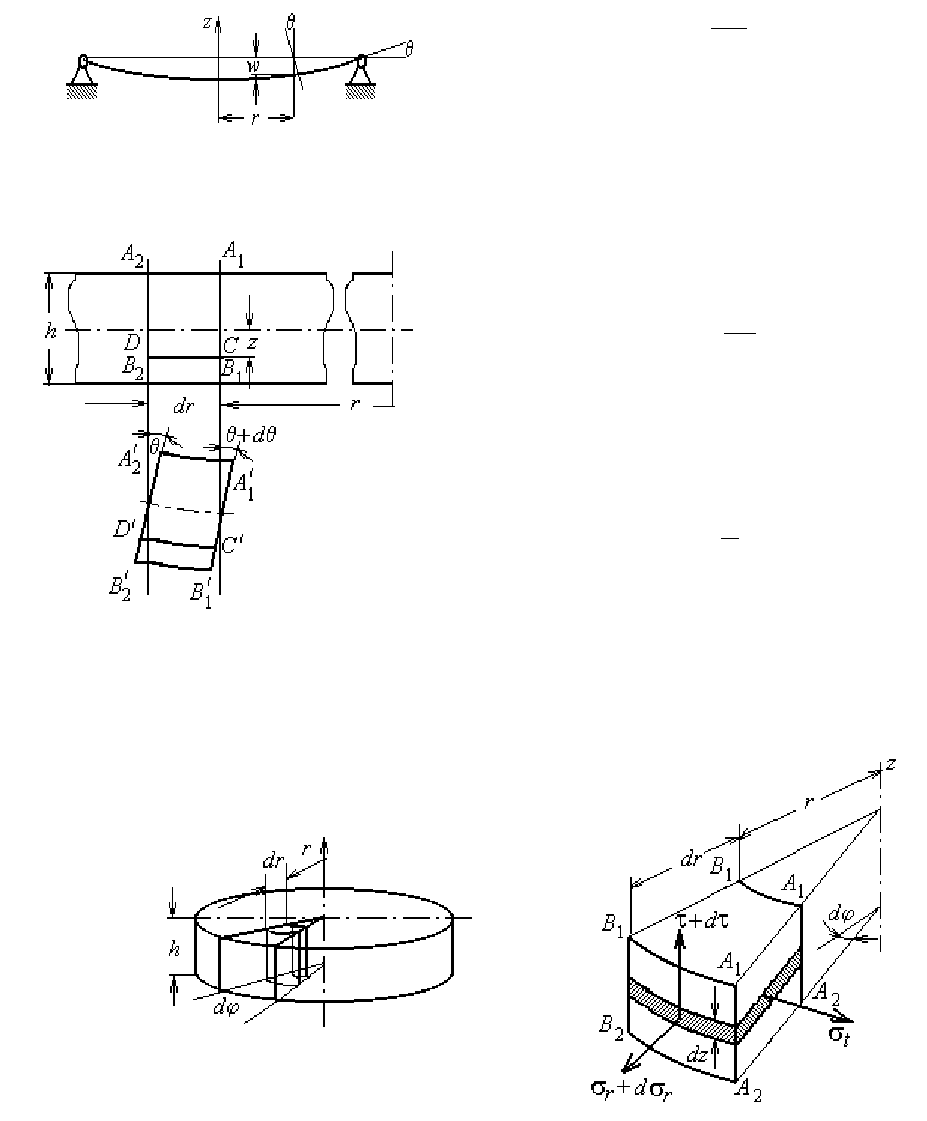
Под действием внешних сил пласти-
на (рис. 4.1) меняет свою кривизну одно-
временно в двух плоскостях. Форма полу-
ченной упругой поверхности характеризу-
ется законом изменения прогибов w. Если
допустить, что прогибы много меньше
толщины пластины h, т.е. w<<h, то изгиб
пластины можно рассматривать независимо от ее растяжения.
При расчете тонких
пластин вводятся также допущения:
а) точки, расположенные на некоторой прямой, нормальной к средин-
ной поверхности до деформации, нормальны к ней и после деформации;
б) нормальные напряжения в сечениях, параллельных срединной по-
верхности, пренебрежимо малы по сравнению с изгибными.
Рис. 4.1
66
4.1. Расчет круглых, симметрично нагруженных пластин
Рассмотрим пластину постоянной толщины h, нагруженную силами
симметрично оси z (рис. 4.2). Прогиб пластины w и угол поворота нормали θ
являются функцией только радиуса r и связаны соотношением
dr
dw
−=θ . (4.1)
Рассмотрим элемент в осевом сечении
пластины (рис. 4.3). Нормаль А
1
В
1
повернется
на угол θ, а нормаль А
2
В
2
– на угол θ+dθ. От-
резок CD на расстоянии z от срединной по-
верхности получит удлинение
θ=
θ
−
θ
+
θ
zdzdz )(.
Относительное его удлинение будет
dr
d
z
r
θ
=ε . (4.2)
До изгиба пластины длина окружности,
проходящей через точку С, была равна 2πr, а
после изгиба - 2π(r+zθ). Относительное удли-
нение окружности
r
z
t
θ
=ε . (4.3)
Двумя осевыми сечениями под углом
dϕ друг к другу и двумя цилиндрическими
сечениями с радиусами r и r+dr выделим из
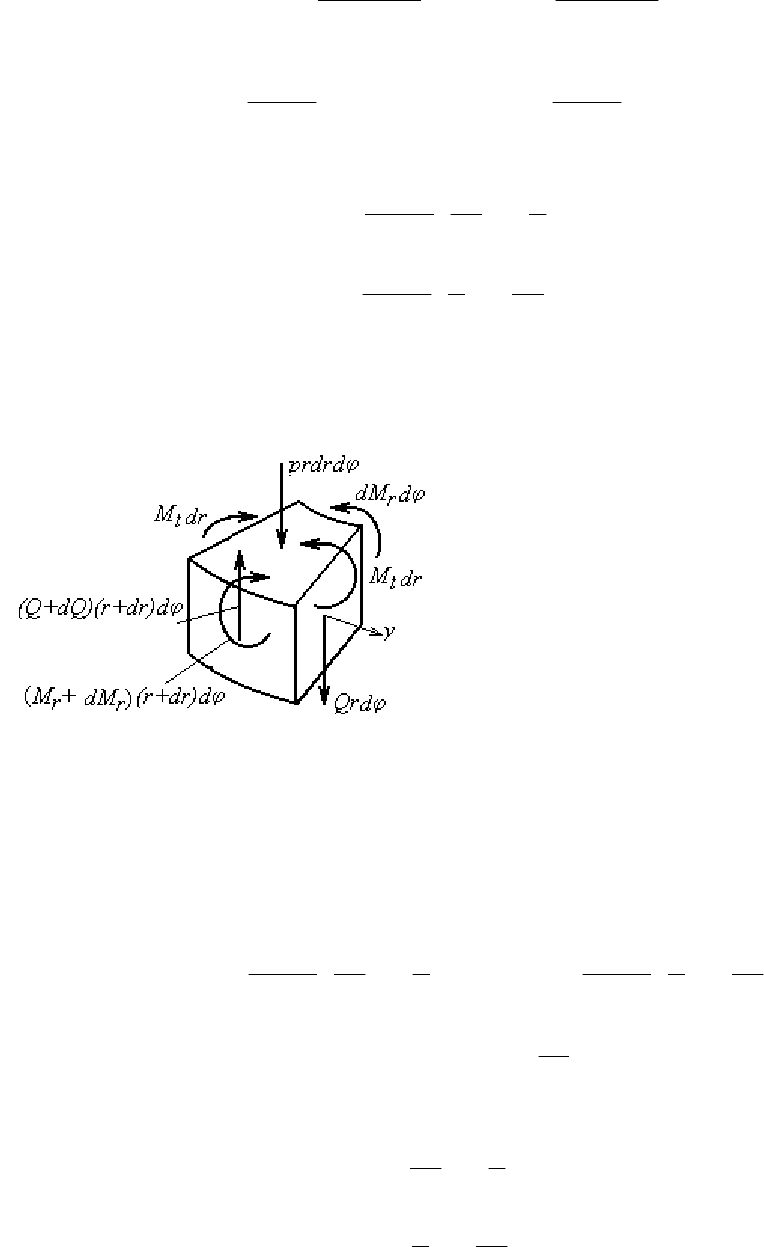
пластины элементарную призму (рис. 4.4).
Рис. 4.4
Связь между удлинениями и напряжениями определяется законом Гука
в виде
Рис. 4.2
Рис.4.3
67
E
E
rt
t
tr
r
μ
σ
+
σ
=ε
μ
σ
+
σ
=ε ;.
Выразим напряжения через деформации
)(
1
);(
1
22
rtttrr
EE
με+ε
μ−
=σμε+ε
μ−
=σ .
Согласно выражениям (4.2) и (4.3), получим
⎟
⎠
⎞
⎜
⎝
⎛
θ
μ+
θ
μ−
=σ
rdr
dEz
r
2
1
; (4.4)
⎟
⎠
⎞
⎜
⎝
⎛
θ
μ+
θ
μ−
=σ
dr
d
r
Ez
t
2
1
. (4.5)
На гранях призмы, кроме нормальных, возможно возникновение каса-
тельных напряжений τ в вертикальном направлении перпендикулярно радиу-
су.
Рассмотрим условие равновесия
выделенной призмы (рис 4.5). Введем
обозначения:
Q – перерезывающая сила, при-
ходящаяся на единицу длины, (для со-
кращения – поперечная сила);
М – моменты, приходящиеся на
единицу длины (для сокращения
– просто моменты).
Зная
r
и
t
, определим равнодей-
ствующие моменты на гранях
∫∫
−−
σ=σϕ=ϕ
2/
2/
2/
2/
.;
h
h
tt
h
h
rr
zdzdrdrMzdzrdrdM
Используя выражения (4.4) и (4.5), получим
;
1
;
1
22
Int
dr
d
r
E
MInt
rdr
dE
M
tr
⎟
⎠
⎞
⎜
⎝
⎛
θ
μ+
θ
μ−
=
⎟
⎠
⎞
⎜
⎝
⎛
θ
μ+
θ
μ−
=
∫
−
==
2/
2/
3
2
12
h
h
h
dzzInt
.
Отсюда следует
;
⎟
⎠
⎞
⎜
⎝
⎛
θ
μ+
θ
=
rdr
d
DM
r
(4.6)
,
⎟
⎠
⎞
⎜
⎝
⎛
θ
μ+
θ
=
dr
d
r
DM
t
(4.7)
где D – жесткость пластины, равная
Рис. 4.5

68
)1(12
2
3
μ−
=
Eh
D .
К элементу также приложена сила prdrdϕ. Проектируя все силы на ось
симметрии, получим
0))((
=
ϕ
−
ϕ
−
ϕ
+
+
p
rdrdQrddd
r
r
dQQ ,
откуда
)(Qr
dr
d
pr = .
Сумма моментов всех сил относительно оси у, касательной к дуге ра-
диуса r в срединной плоскости, равна
0))((
2
))(( =ϕ+++ϕ−ϕ−ϕ−++ drddrrdQQ
dr
prdrddrdMrdMdrrdMM
trrr
.
Пренебрегая величинами высшего порядка малости и переходя к пределу,
получим
QrrM
dr
d
M
rt
=−= )(.
Заменяя моменты M
t
и M
r
их выражениями и полагая жесткость D постоян-
ной, имеем
D
Qr
rdr
d
d
r
d
r −=
θ
−
θ
+
θ
2
2
,
откуда
D
Q
r
dr
d
rdr
d
−=
⎥
⎦
⎤
⎢
⎣
⎡
θ⋅ )(
1
.
После двукратного интегрирования находим
∫∫
−+=θ drQdrr
D
r
r
C
rC )(
1
2
1
. (4.8)
Постоянные интегрирования С
1
и С
2
определяются граничными условиями
для каждого конкретного случая.
После того как функция θ найдена, по уравнениям (4.6) и (4.7) опреде-
ляются моменты M
t
и M
r
, а также прогиб w по формуле (4.1). По величинам
моментов находятся напряжения
z
h
M
r
r
3
12
=σ ; (4.9)
z
h
M
t
t
3
12
=σ . (4.10)
Наибольшие напряжения имеют место при
2
h
z ±=
,
поэтому
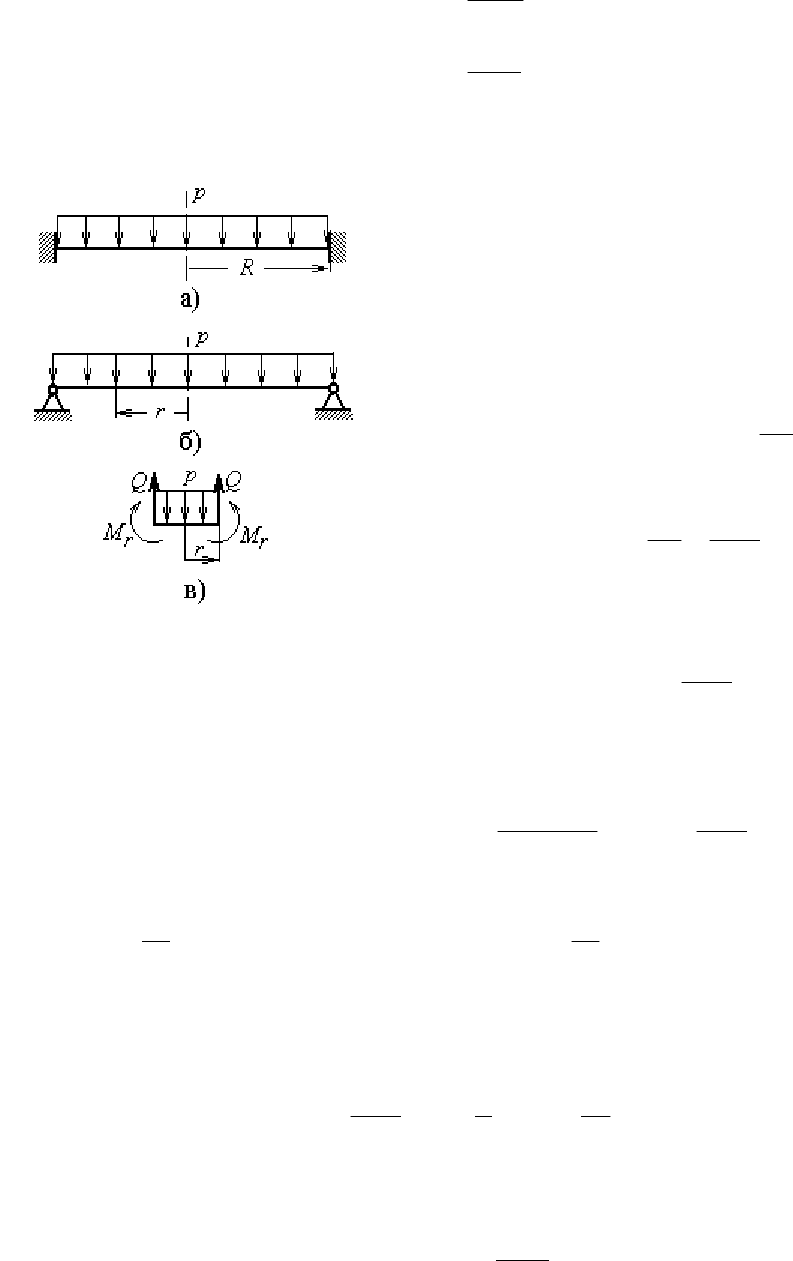
69
2
max
6
h
M
r
r
±=σ ; (4.11)
2
max
6
h
M
t
t
±=σ . (4.12)
ПРИМЕР 4.1. Определить напряжения и перемещения в круглой пла-
стине, нагруженной распределенной нагрузкой р:
а) при защемлении пластины по конту-
ру;
б) при свободном опирании пластины на
контур.
РЕШЕНИЕ. Определим схемы нагруже-
ния на рис. 4.6. Для центра пластины уравне-
ние равновесия дает
2
;2
2
pr
QrprQ =π=π⋅ .
Из выражения (4.8) имеем
D
pr
r
C
rC
16
3
2
1
−+=θ .
При r=0 уравнение теряет смысл, так как
θ=0, поэтому С
2
=0 и
D
pr
rC
16
3
1
−=θ
.
Случай защемлении пластины.
При r=R θ=0, откуда
)(
16
;
16
32
2
1
rrR
D
pDpR
C −=θ= .
Далее,
)3()1([
16
22
μ+−μ+= rR
p
M
r
; )31()1([
16
22
μ+−μ+= rR
p
M
t
.
Эпюры моментов представлены на рис. 4.7,а. Из уравнения (4.1)
d
r
dw
θ
−
=
,
откуда
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+−=
42
1
16
4
22
3
r
rRC
D
p
w
.
Постоянная С
3
определяется из граничных условий:
при r=R w=0, тогда
2224
3
)(
64
;25,0 rR
D
p
wRC −== .
На основании полученных уравнений видно, что пластина изгибается
по поверхности четвертого порядка.
Рис. 4.6. Схемы нагружения:
а – при защемлении;
б – при свободном опирании;
в – определение поперечной
силы

70
Рис. 4.7. Эпюры изгибающих моментов:
а – при жестком защемлении пластины; б – при ее свободном опирании
Случай свободного опирания.
На контуре при r=0 σ
r
=0 и М
r
=0, откуда
0=
μ
θ
+
θ
rdr
d
.
Подставим выражение θ, получим
0
1616
3
2
1
2
1
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−μ+−
D
pR
C
D
pR
C ,
откуда
⎟
⎠
⎞
⎜
⎝
⎛
−
μ+
μ+
=θ
μ+
μ+
=
32
2
1
1
3
16
;
)1(16
)3(
rR
D
p
D
pR
C
.
Изгибающие моменты, эпюры которых представлены на рис.4.7,б, оп-
ределяются по уравнениям
))(3(
16
22
rR
p
M
r
−μ+= ;
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
−+=
22
3
31
)3(
16
rR
p
M
t
μ
μ
μ
.
Выражение для перемещения
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+⋅
μ+
μ+
−=θ−=
421
3
16
;
422
3
rrR
C
D
p
wdrdw .
При r=R w=0, откуда
μ+
μ+
⋅=
1
5
4
4
3
R
C ,
поэтому
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+⋅
μ+
μ+
−
μ+
μ+
⋅=
421
3
1
5
416
4224
rrRR
D
p
w .
Максимальные прогибы в первом и втором случае будут соответствен-
но равны
D
pR
w
64
4
max
=
и
D
pR
w
4
max
1
5
⋅
μ+
μ+
= .
