Беляев В.М., Миронов В.М. Конструирование и расчет элементов оборудования отрасли. Часть 1: Тонкостенные сосуды и аппараты химических производств
Подождите немного. Документ загружается.

21
2.1. Основы безмоментной теории
Безмоментная теория расчета тонкостенных оболочек предполагает
следующие допущения:
1. Толщина оболочки должна быть достаточно малой по сравнению с
ее другими геометрическими размерами. Например, для цилиндра
2,01,0 −≤
B
R
s
,
где R
В
– внутренний радиус оболочки.
Вследствие малой толщины нормальные напряжения растяжения или
сжатия по толщине оболочки не изменяются, величина их в R
B
/s раз больше
изгибных, что и определяет безмоментное состояние.
2. По форме сосуд обязательно должен представлять оболочку враще-
ния.
3. Нагрузка (давление на стенки) должна быть симметричной относи-
тельно оси вращения.
Давление на стенки может изменяться вдоль оси вращения, например,
при наличии жидкости в вертикальном аппарате. Такой аппарат можно счи-
тать
по мембранной теории, однако если его положить горизонтально, то на-
грузка станет несимметрична оси и использование теории будет невозможно.
Оболочкой вращения называется оболочка,
срединная поверхность которой образована враще-
нием какой-либо плоской кривой вокруг оси, лежа-
щей в ее плоскости. Срединная поверхность – это
поверхность, равноотстоящая от внутренней и на-
ружной стенок
оболочки. Радиусы кривизны мери-
дионального и кольцевого сечений срединной по-
верхности
R
1
=bO≈dO, R
2
=aA≈bA.
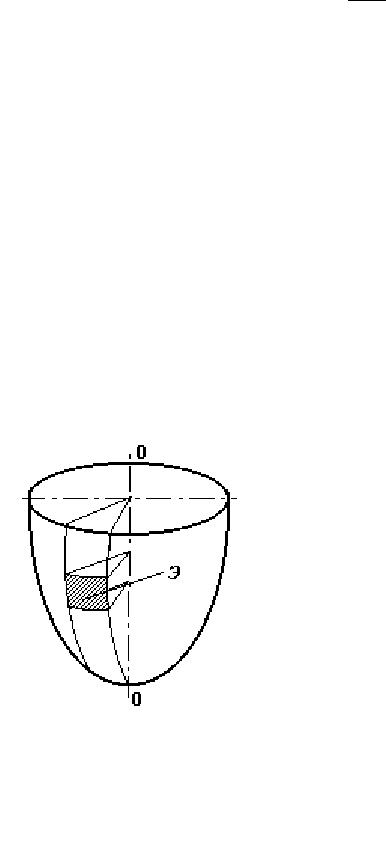
Для определения усилий и напряжений в
оболочке вращения (рис. 2.1) от действия внут-
реннего давления р выделим методом сечений
элемент Э, образованный двумя меридиональными и двумя кольцевыми се-
чениями.
Меридиональное сечение – это сечение оболочки плоскостью,
проходящей через ось вращения.
Кольцевое сечение – это сечение оболочки конической поверхностью с
вершиной на
оси вращения и с образующими, пересекающими поверхность
оболочки под прямым углом.
Рис. 2.1. Схема обо-
лочки вращения
22
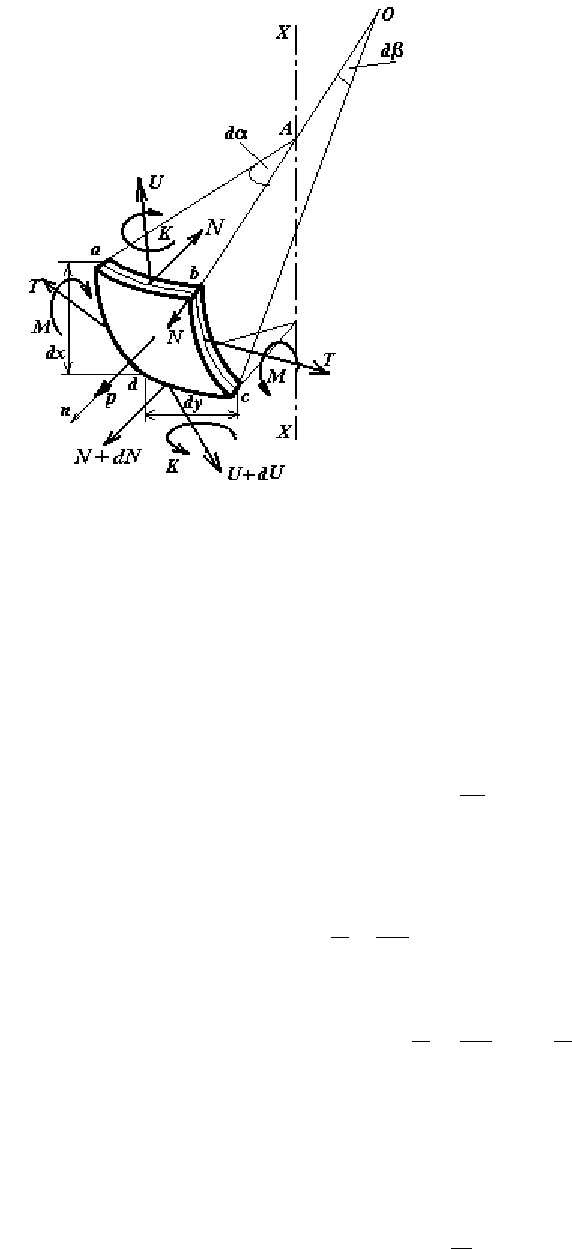
На выделенный элемент Э действуют
силы и моменты, указанные на рис. 2.2.
Рассмотрим условие равновесия выделен-
ного элемента Э.
Так как рассматривается безмомент-
ная теория, то принимают K=M=N=0,
где K – кольцевой момент на единицу
длины меридиана срединной поверхности;
М – меридиональный момент на
единицу длины кольцевого сечения сре-
динной
поверхности;
N – перерезывающая сила на едини-
цу длины кольцевого сечения срединной
поверхности.
Действующие силы, не равные нулю:
U – меридиональная сила на едини-
цу длины кольцевого сечения срединной
поверхности;
Т – кольцевая сила на единицу дли-
ны меридиана срединной поверхности.
Запишем уравнение равновесия элемента в проекциях на нормаль n к
срединной
поверхности.
На грани ab длиной dy действует нормальное меридиональное напря-
жение σ
m
:
s
U
m
=σ . (2.1)
Тогда меридиональная сила упругости, действующая на грань ab,
sdyUdy
m
σ
=
.
Она действует под углом
22
β
+
π d
к нормали, поэтому ее проекция на нормаль
будет
βσ−≈
⎟
⎠
⎞
⎜
⎝
⎛
β
+
π
σ sdyd
d
sdy
mm
2
1
22
cos .
Сила, действующая на грань
cd, дает, без учета бесконечно малой
третьего порядка, такую же проекцию на нормаль
n.
На гранях
ac и bd длиной dy действует нормальное кольцевое напряже-
ние σ
t
:
s
T
t
=σ . (2.2)
Тогда кольцевая сила упругости, действующая на гранях
ac и bd
sdxTdx
t
σ
=
.
Рис. 2.2. Схема действия сил
и моментов на элемент Э
23
Эта сила составляет с нормалью угол
22
α
+
π
d
. Ее проекция на нормаль
ασ−≈
⎟
⎠
⎞
⎜
⎝
⎛
α
+
π
σ sdxd
d
sdx
tt
2
1
22
cos .
Сила от действия внутреннего давления р P=pdxdу.
Алгебраическая сумма проекций всех сил должна быть равна нулю. То-
гда
0
=
−
α
σ
+
β
σ pdxdysdxdsdyd
tm
.
Так как
1
Rddx
β
=
и
2
Rddy
α
=
, получим окончательно уравнение
Лапласа
s
p
RR
tm
=
σ
+
σ
21
. (2.3)
Для расчета одного уравнения с двумя неизвестными недостаточно, по-
этому следует найти еще одно уравнение. Таковым будет уравнение равнове-
сия зоны оболочки.
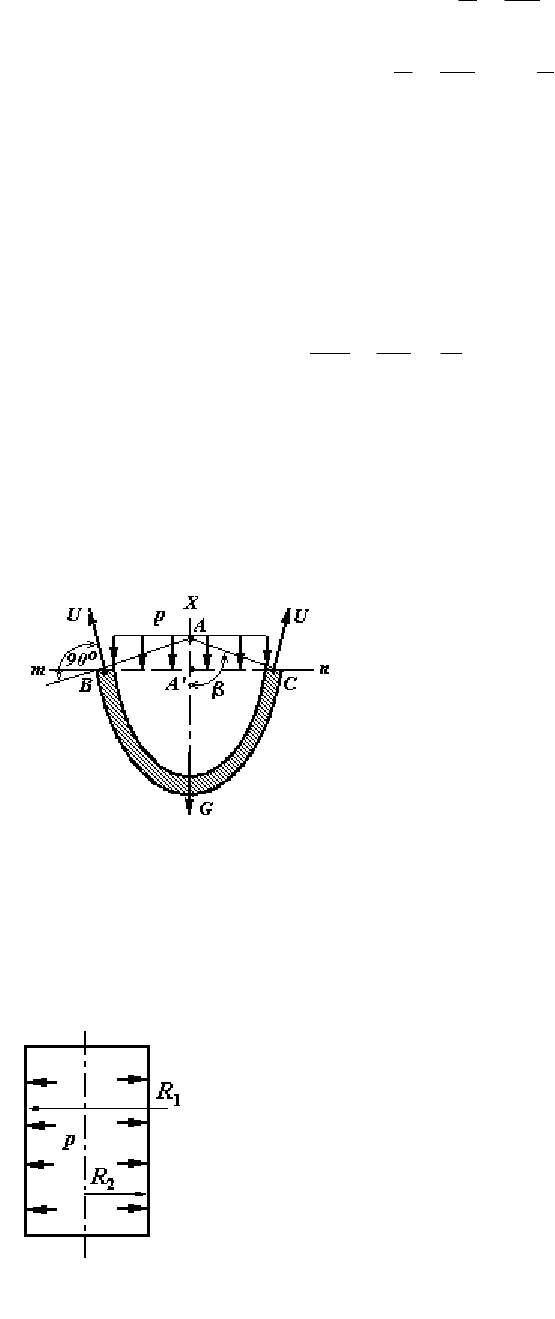
Рассмотрим условие равновесия зоны оболочки ниже уровня ее опоры
(рис. 2.3). Кольцевым сечением выделим эту зону на уровне mn. На зону дей-
ствуют силы:
- от давления среды p
на уровне mn;
- вес оболочки и содержимого в зоне G;
- сила упругости U – меридиональная сила.
Так как расчет производится по безмоментной
теории, то моменты и перерезывающие силы
принимаются равными нулю.
В соответствии с рисунком:
2
RACAB
=
=
.
r
CA
B
A =
=
//
;
β
= sin
2
Rr .
Тогда уравнение равновесия зоны оболоч-
ки, т.е. сумма проекций всех сил на ось Х, будет
0sinsin2
22
2
2
2
=βπ−βπσ GRpsR
m
∓ , (2.4)
где знак (-) характерен для данного случая, а (+) – когда сечение mn находит-
ся выше уровня опоры и рассматривается верхняя отсеченная часть.
Используя уравнения (2.1) – (2.4) можно получить
расчетные формулы для вычисления напряжений в любой
точке оболочки вращения.
Тонкостенная цилиндрическая оболочка, нагруженная
внутренним газовым давлением р (рис. 2.4). Радиусы мери-
дионального и кольцевого сечений равны
соответственно
R
1
=∞; R
2
=R,
где R – радиус цилиндра.
Тогда, по уравнению Лапласа (равновесия элемента оболочки),
Рис. 2.3. Равновесие
зоны оболсчки
Рис. 2.4
24
s
pR
pRTp
R
T
R
U
t
=σ==+ ;;
1
.
Из уравнения равновесия зоны оболочки (без учета веса среды и оболочки)
получим
;
2
;0sinsin2
π
=β=β−β pRU
s
pRpR
U
m
2
;
2
=σ= .
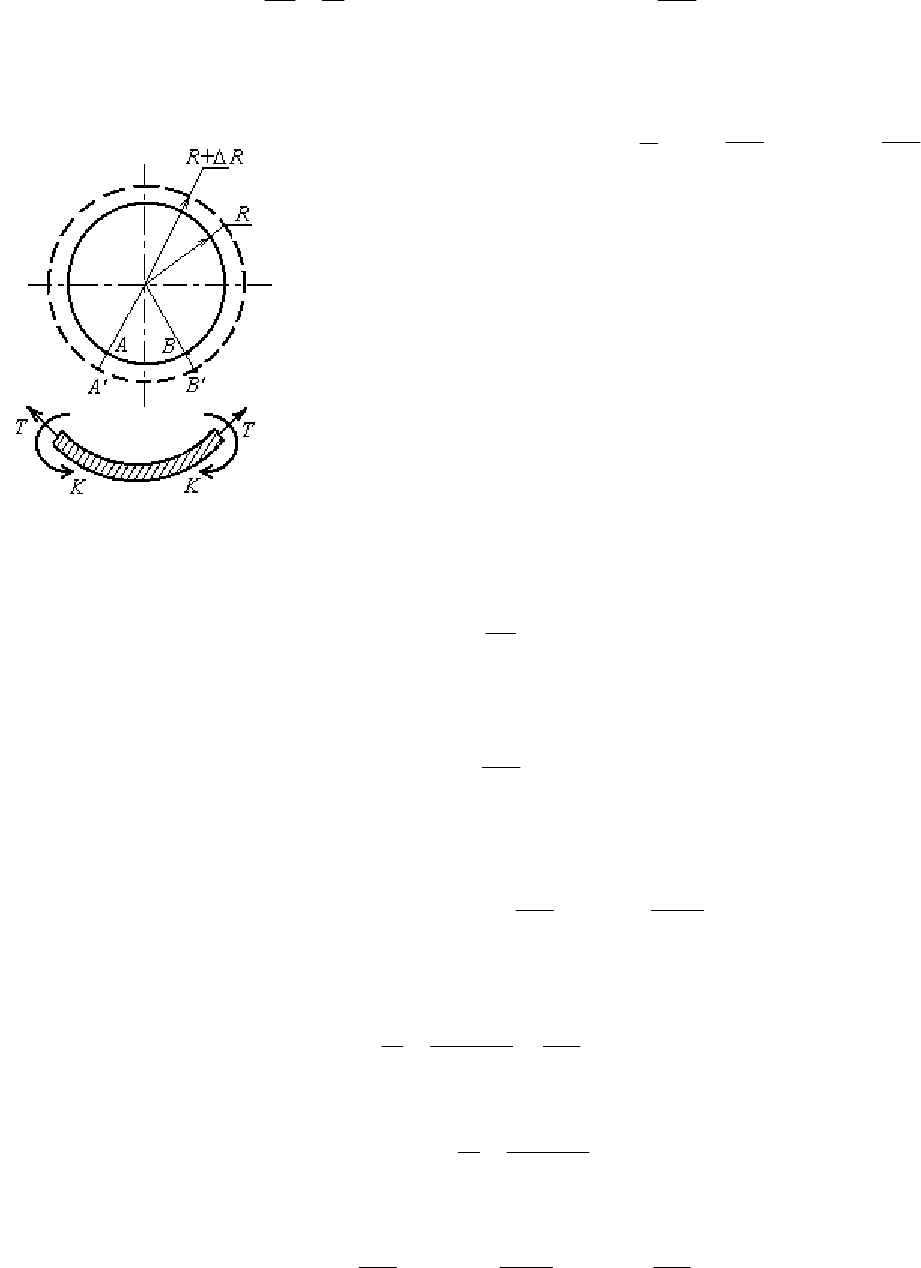
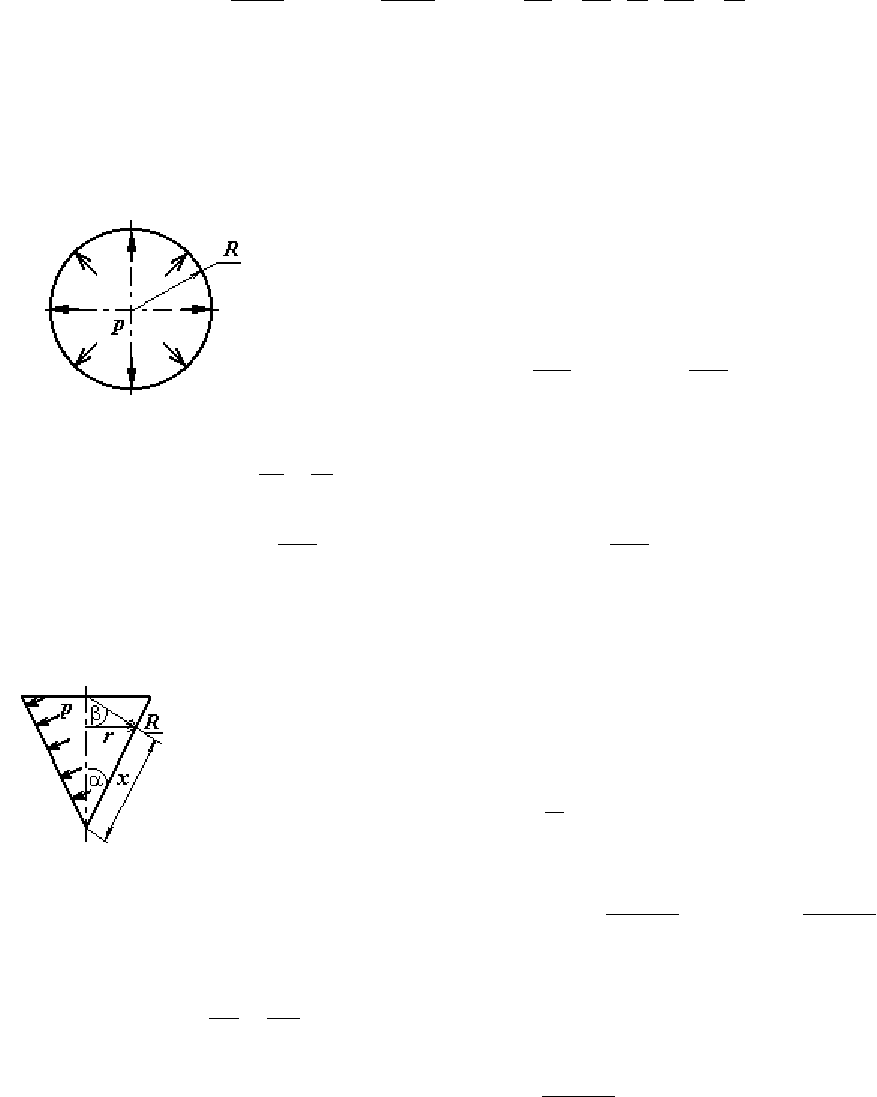
В действительности в результате действия нор-
мальных напряжений в стенке тонкостенного сосуда
все же возникают изгибающие моменты, изменяющие
кривизну оболочки. Для оценки их значения рассмот-
рим определение кольцевых моментов в цилиндриче-
ской оболочке (рис. 2.5).
В результате упругой деформации от давления р
дуга АВ принимает размер А
/
В
/
. Это происходит за
счет растягивающих сил Т. Кривизна дуги уменьшает-
ся за счет действия кольцевых моментов К, лежащих в
плоскости кольца.
Относительное удлинение элемента цилиндра
определяется по формуле
E
t
σ
=ε ,
где Е – модуль упругости материала цилиндра.
Для цилиндрической обечайки
sE
pR
=ε .
Под влиянием момента К изменяется кривизна элемента, т.е. радиус R полу-
чает приращение
ΔR:
sE
pR
RR
sE
pR
RRRRR
2
+=+=ε+=Δ+
.
Величину изменения кривизны элемента под влиянием момента К
можно выразить так:
EJ
K
RRR
=
Δ
+
−
11
,
откуда
⎟
⎠
⎞
⎜
⎝
⎛
Δ+
−=
RRR
EJK
11
.
Преобразуя выражение в круглых скобка и учитывая, что R
2
>>RΔR, получим
s
pJ
K
sE
pR
R
R
R
EJK ==Δ
Δ
= ;;
2
2
.
Рис. 2.5
25
Относя кольцевой момент к единице длины стенки, т.е. к прямоуголь-
нику длиной 1 и шириной s, находим
2
6
12
;
6
1
;
12
1
2
323
p
s
s
ps
W
Ks
W
s
J =⋅⋅==σ
⋅
=
⋅
= .
Таким образом, величина напряжения от изгиба в цилиндрической
обечайке равна примерно p/2, что в R/s раз меньше σ
t
.
Тонкостенная сферическая оболочка, нагруженная внутренним газо-
вым давлением р (рис. 2.6). Радиусы меридионального и кольцевого сечений
равны радиусу шара: R
1
=R
2
=R.
По уравнению равновесия зоны оболочки (без
учета веса среды и оболочки) получим
0sinsin2
=
β
−
β
p
R
U
;
s
pRpR
U
m
2
;
2
=σ= .
Из уравнения Лапласа
;; pRTUp
R
T
R
U
=+=+
.
2
;
2
s
pR
pRT
pR
mt
=σ=σ=+
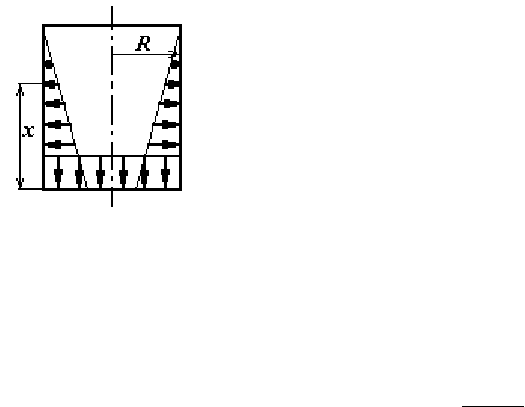
Тонкостенная коническая оболочка, нагруженная внутренним газовым
давлением р (рис. 2.7).
Для возможного применения уравнения равновесия зо-
ны оболочки выразим текущий радиус и угол β через из-
вестные величины
α=βα−
π
=βα= cossin;
2
;sinxr .
Тогда (без учета веса среды и оболочки) получим
s
pxpx
UpxU
m
2
tg
;
2
tg
;0sincos2
α
=σ
α
==α−α .
По уравнению Лапласа
;tg)(;;
21
21
α==∞==+ xxRRRp
R
T
R
U
s
px
pxT
t
α
=σα=
tg
;tg .
Полученные формулы применимы для конических оболочек с углом
при вершине конуса 2α≤160°.
Рис. 2.6
Рис. 2.7
26
Тонкостенная цилиндрическая оболочка, нагруженная внутренним гид-
ростатическим давлением жидкости плотностью ρ (рис.
2.8).
В случае опоры оболочки на днище гидростатиче-
ское давление столба жидкости вызывает только кольце-
вые напряжения. Без учета веса оболочки меридиональная
сила и меридиональные напряжения равны нулю, т.е.
0;0
=
σ
=
m
U
.
Тогда из уравнения Лапласа, при R
2
=R и гидростатиче-
ском давлении на высоте уровня жидкости x, равном ρgx,
кольцевая сила Т будет равна
gxR
T
ρ
=
.
Соответственно кольцевые напряжения
s
gxR
t
ρ
=σ .
2.2. Основы расчета тонкостенных сосудов,
работающих под внутренним давлением
Согласно безмоментной теории расчета на прочность в каждом элемен-
те тонкостенного сосуда действует два напряжения – меридиональное σ
m
и
кольцевое σ
t
, причем всегда σ
t
≥σ
m
.
Продольные и поперечные швы обечаек сварных стальных сосудов и
аппаратов должны быть только стыковыми. Допускается тавровое соедине-
ние при приварке плоских днищ, фланцев и т.п. В продольных сечениях тон-
костенных сосудов кольцевые напряжения больше меридиональных (за ис-
ключением сферических оболочек), поэтому при раскрое листов следует
обеспечить минимум продольных швов
в обечайке. Продольные швы в
смежных обечайках должны быть смещены относительно друг друга не ме-
нее чем на 100 мм. Не рекомендуется делать отверстия по продольным швам.
Мембранная теория не учитывает радиальных (σ
r
) и изгибающих (σ)
напряжений (в принципе σ
r
=р, σ=p/2) вследствие их малости по сравнению с
кольцевыми и меридиональными. Поэтому для расчета толщины стенки тон-
костенных оболочек применяют третью теорию прочности:
minmaxэкв
σ
−
σ
=
σ
,
где σ
экв
– эквивалентное напряжение;
σ
max
– максимальное напряжение;
σ
min
– минимальное напряжение.
Условие прочности имеет вид ][
экв
σ
≤
σ
.
В случае мембранной теории
0;
minmax
≈
σ
=
σ
σ
=
σ
rt
. Тогда
t
σ
=
σ
экв
, или ][
σ
≤
σ
t
.
Рис. 2.8
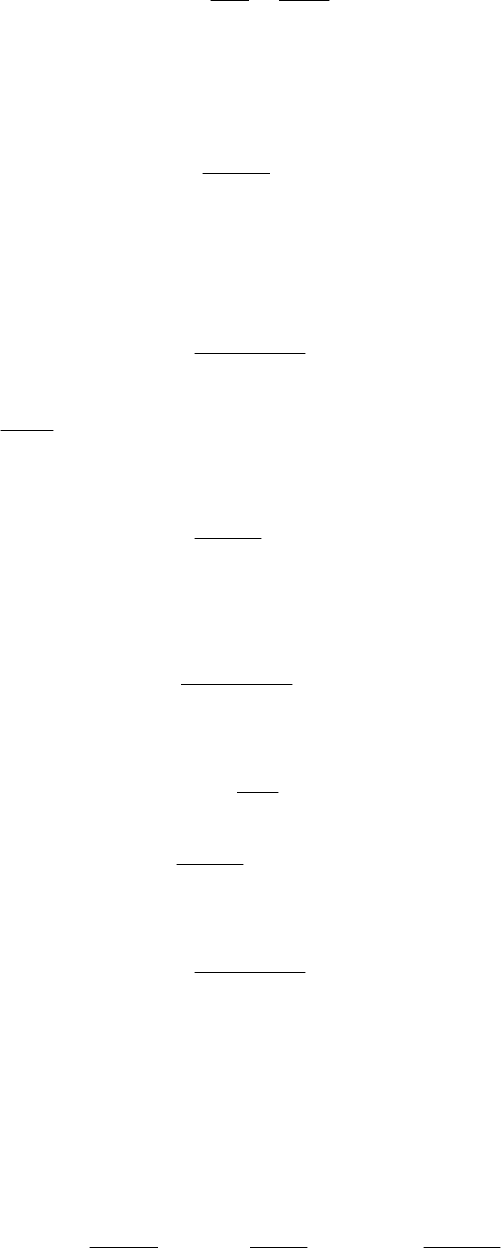
27
Если принять, что ][
σ
=
σ
t
, то для случая тонкостенного цилиндра
можно получить расчетную формулу для толщины стенки
][2][ σ
=
σ
=
pDpR
s
R
, (2.5)
где D – срединный диаметр цилиндрической обечайки.
Учитывая наличие сварных швов, исполнительная толщина стенки ци-
линдра будет
c
pD
s +
ϕσ
=
][2
,
где ϕ - коэффициент прочности продольного сварного шва.
Подставляя в уравнение (2.5) вместо диаметра D срединной поверхно-
сти внутренний диаметр обечайки
RB
sDD
−
=
, получим для цилиндра
c
p
pD
s
B
+
−ϕσ
=
][2
. (2.6)
При соотношении
50
][
≥
ϕσ
p
величиной р в знаменателе уравнения (2.6) мож-
но пренебречь и использовать упрощенное уравнение
c
pD
s
B
+
ϕσ
=
][2
. (2.6)
Используя при расчете в качестве базового наружный диаметр цилинд-
ра, т.е.
R
sDD +=
н
, получим
c
p
pD
s +
+ϕσ
=
][2
н
.
Рассматривая аналогичным образом сферическую оболочку, имеем
0;
4
minmax
≈σ=σ=σ=σ=σ=σ
rUt
s
pD
.
Тогда
c
pD
s +
ϕσ
=
][4
, или
c
p
pD
s
B
+
−ϕσ
=
][4
. (2.8)
Рассматривая коническую обечайку, можно полагать, что максималь-
ные меридиональные и кольцевые напряжения будут на расстоянии l от вер-
шины конуса, где l – длина образующей конической оболочки. Тогда
0;
minmax
≈
σ
=
σ
σ
=
σ
rt
;
α
=σ
α
=
α
=σ=σ
cos
][;
sin
;
tg
][
s
pRR
l
s
pl
R
t
.

28
Окончательно
c
p
pD
s
B
+
−αϕσ
=
cos][2
. (2.9)
2.3. Основы расчета тонкостенных сосудов,
работающих под наружным давлением
При работе обечаек под внутренним давлением в их стенках возникают
нормальные растягивающие напряжения, а при их работе под наружным дав-
лением – сжимающие напряжения. Поэтому при расчете на прочность обеча-
ек, работающих под наружным давлением, можно использовать формулы,
выведенные для обечаек, работающих под внутренним давлением. Однако
наличие наружного давления может привести к
потере устойчивости формы
оболочки.
Из теории расчета на устойчивость упругих стержней следует, что
стержень легко выдерживает растягивающую нагрузку и не выдерживает оп-
ределенной, т.н. критической, нагрузки при сжатии. При постепенном на-
гружении стержня сжимающей нагрузкой сохраняется одна и та же форма
устойчивого равновесия. По достижении критической величины нагрузки
скачком
теряется первоначальная форма стержня и появляется новая форма
устойчивого равновесия.
Это относится и к другим конструкциям, где возникают деформации
сжатия. Так, тонкостенные сосуды, работающие под наружным давлением,
должны иметь более прочную конструкцию, чем такие же аппараты, рабо-
тающие под внутренним давлением.
Давление, при котором тонкостенные сосуды теряют устойчивость
формы, называется критическим
. Под действием такого давления попереч-
ное сечение первоначально круглой обечайки приобретает волнообразную
форму, причем напряжения сжатия в ее стенках могут быть меньше предела
текучести материала элемента аппарата.
Потеря устойчивости формы цилиндрической оболочки может про-
изойти и при давлении ниже критического в случае овальности ее попереч-
ного сечения, которое ограничивается нормами.
Овальность стальных свар-
ных сосудов при нагружении их наружным давлением не должна быть менее
0,005D, но не более 20 мм, а для корпусов теплообменников – не более 7 мм.
Величина критического давления зависит от геометрической формы,
размеров аппарата и от механических свойств материала его стенок.
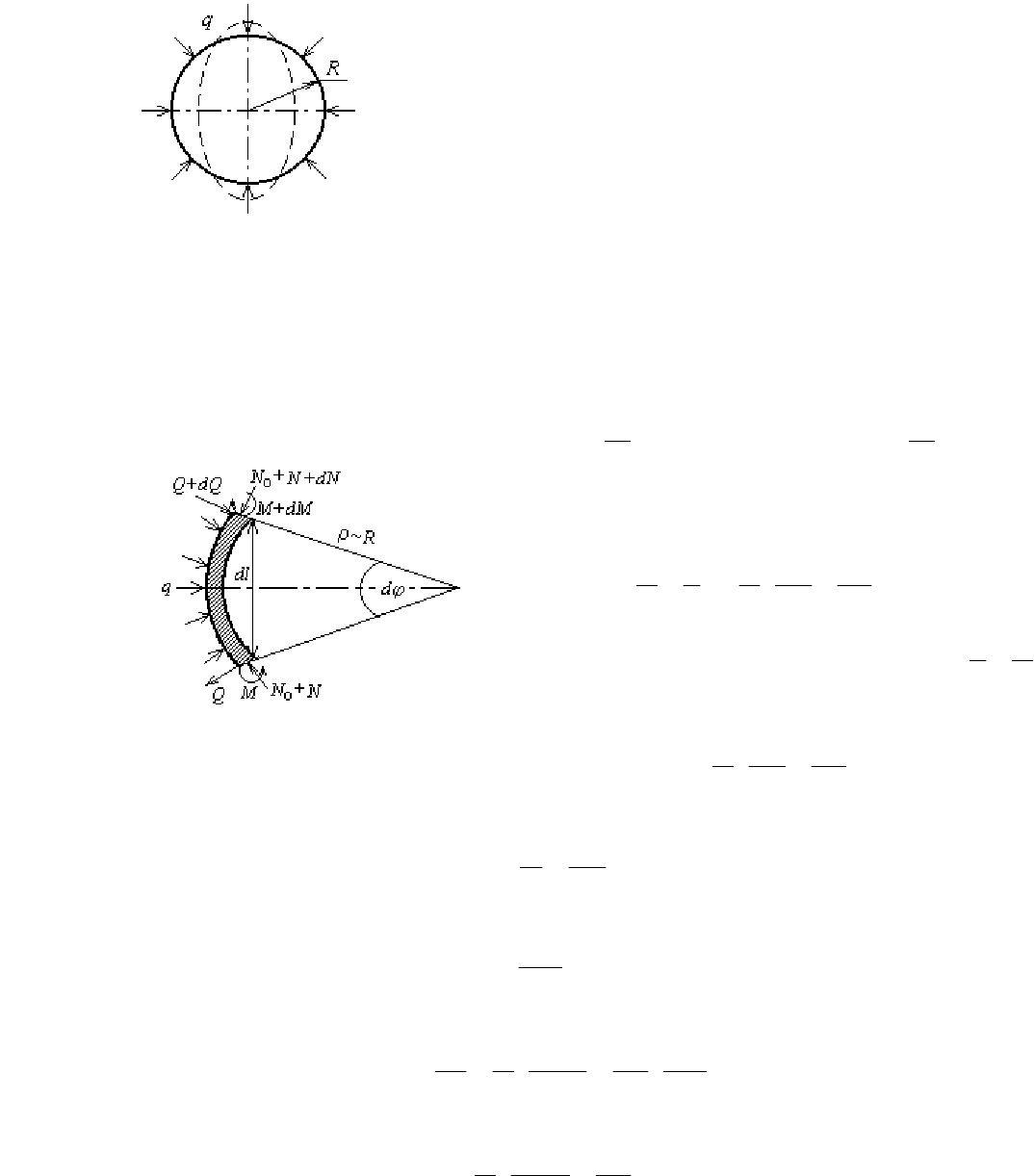
Определение критического давления. Рассмотрим задачу об устойчиво-
сти
кольца, сжатого равномерно распределенной нагрузкой интенсивности q
(рис. 2.9).
При некотором значении этой нагрузки круговая форма кольца стано-
вится неустойчивой и оно изгибается, принимая примерно форму эллипса.
29
Выделим из изогнутого кольца элементарный участок длиной dl (рис.
2.10). Местный радиус кривизны будем считать рав-
ным R, т.е. ρ≈R. В сечениях кольца возникают нор-
мальные силы и изгибающие моменты. Нормальная
сила состоит из двух слагаемых:
N
0
– нормальная сила до потери устойчи-
вости;
N – изменение нормальной силы вследст-
вие изгиба кольца.
Таким образом, N
0
+N – нормальная сила после потери устойчивости.
Из условия равновесия в докритическом состоянии
qRN =
0
.
Рассмотрим условие равновесия изогнутого элемента. Спроектируем
все силы на направление нормали и запишем, полагая, что
ρ
=ϕ
dl
d
,
0)(
0
=
ρ
+−+
dl
NNdQqdl
.
Далее, подставляя значение qRN =
0
, полу-
чим
0
111
=
ρ
−⋅+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ρ
−
R
N
dl
dQ
RR
q .
Обозначая изменение кривизны
R
11
−
ρ
=χ
и учитывая, что ρ≈R, получим
0
1
2
=−⋅+χ−
R
N
dL
dQ
R
q .
Составим еще два возможных уравнения равновесия:
;0=+
dl
dN
R
Q
0=+ Q
dl
dM
.
Из трех уравнений исключаем Q и N. Тогда
0
11
23
3
=⋅+⋅+
χ
dl
dM
R
d
l
Md
Rdl
d
q ,
или после интегрирования
1
22
2
11
CM
R
d
l
Md
R
q =+⋅+χ . (2.10)
Изгибающий момент связан с изменением кривизны известным соот-
ношением
Рис. 2.9
Рис. 2.10
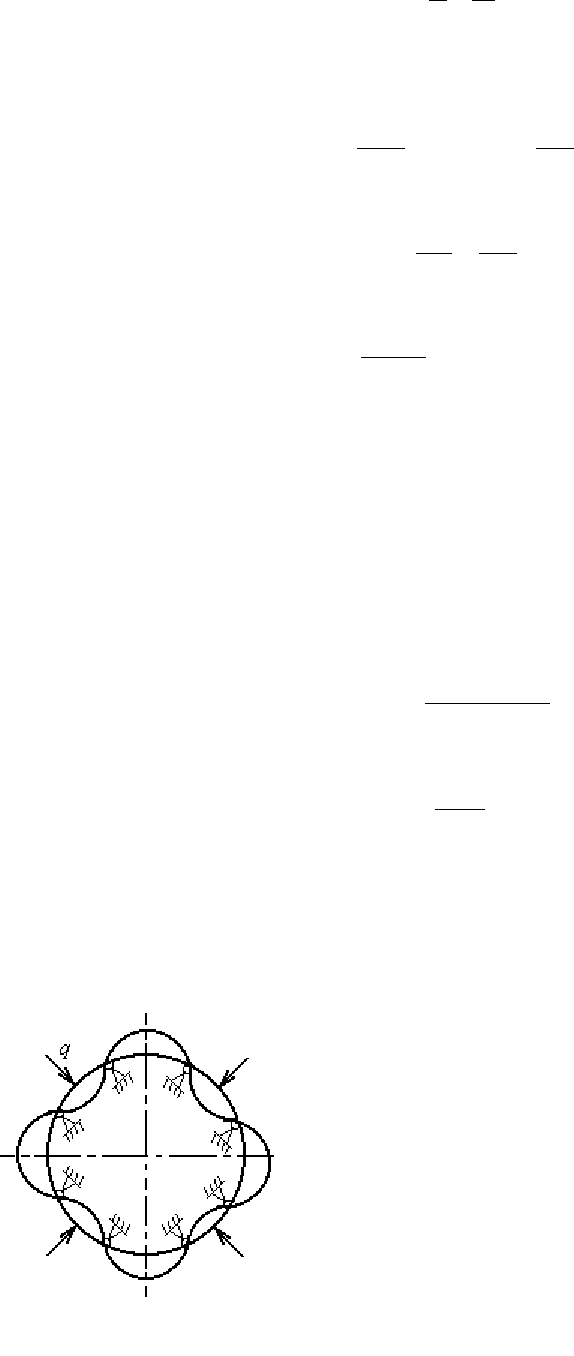
30
χ=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
ρ
= EJ
R
EJM
11
.
Исключая из (2.10) момент М, получаем уравнение относительно одного не-
известного χ
EJ
R
Ck
d
l
d
1
2
2
2
=χ+
χ
, (2.11)
где
EJ
qR
R
k +=
2
2
1
. (2.12)
Решение уравнения (2.11) –
klCklC
EJ
k
R
С cossin
32
2
1
++=χ . (2.13)
Для замкнутого кольца критическую нагрузку можно определить из ус-
ловия периодичности решения (2.13), т.е. если
R
l
π
=
2, то функция χ остает-
ся неизменной. Но для этого необходимо, чтобы kl менялось кратно 2π. По-
этому
nk
l
R
l
k
π
=
−
π
+
2)2(,
где n – любое целое число. Тогда
kR=n.
Подставляя значение k в (2.12), получим
3
2
кр
)1(
R
EJn
q
−
= . (2.14)
Минимальное, отличное от нуля, значение критической нагрузки будет
при n=2, т.е.
3
min
кр
3
R
EJ
q = .
При таком значении нагрузки кольцо теряет свою форму, приобретая оваль-
ность (эллипсность).
Если кольцо подкрепить четным числом (2n при n>2) равноотстоящих
опор (рис. 2.11), то изгиб произойдет по 2n полуволнам и критическое значе-
ние нагрузки можно определить по формуле (2.14) для заданного значения n.
В большинстве случаев для сохранения ус-
тойчивости
формы оболочки целесообразно не уве-
личивать толщину ее стенки, а устанавливать спе-
циальные кольца жесткости, которые будут вос-
принимать часть нагрузки. Они могут располагать-
ся внутри и снаружи аппарата. Их обычно соеди-
няют с обечайкой методом сварки двухсторонними
прерывистыми швами с общей длиной шва не ме-
нее половины длины окружности
кольца в месте
его соединения. Расстояние между сварными уча-
Рис. 2.11
