Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

9.6 Electrons, positrons and neutrinos 423

/ n

−15

−10

−5

0.1

100

/ kT

a) symmetric universe

b) asymmetric universe

thermal equilibrium

electrons

positrons

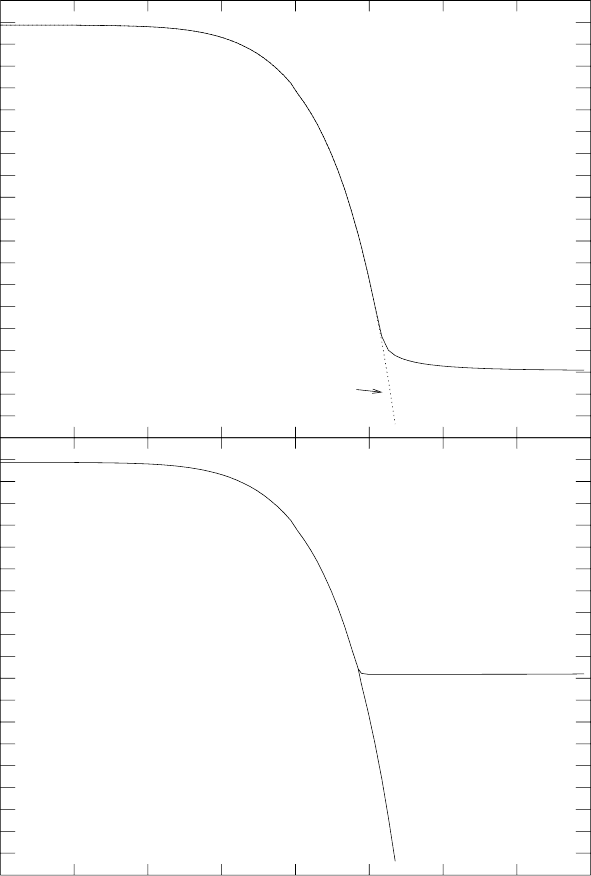
Fig. 9.8. log(n

) versus temperature for a symmetric universe, n

= n

−

= n

(top panel) and for a asymmetric universe, (n

−

− n

)/n

=3× 10

−10

(bottom

panel). For the symmetric universe, the dotted line shows log(n

) in the case of

thermal equilibrium.

424 9. Nuclear Cosmology

wheretheefactorsofkT come for n

and two factors from the cross-section.

Since the annihilation rate is proportional to T

while the expansion rate

(9.56) is proportional to T

, the reaction rate must win at high temperature.

Numerically, one ﬁnds that the annihilation rate is greater than the expansion

rate for kT > 1 MeV so we can conclude that for temperatures greater than 1

MeV, neutrinos were in chemical equilibrium. After the annihilation reactions

freeze-out at T

∼ 1 MeV, the neutrinos decouple and their number density

falls like n

∝ a

−3

We are now in a position to understand why the temperature for rel-

ativistic neutrinos ends up being lower than the photon temperature. For

kT > 1 MeV, photons, neutrinos, and electron–positrons were in thermal

equilibrium with a unique temperature, T

= T

. Apart from factors

due to the Pauli principle and the small electron–positron asymmetry the

numbers of electrons, positrons, neutrinos and photons were equal.

When kT

and kT

dropped below m

the e

−

pairs were transformed

into photons (by e

−

→ γγ) but not into the decoupled neutrinos. After these

annihilations, the number of photons was therefore greater than the number

of neutrinos. Since the distributions are thermal with n ∝ T

, it follows

that T

for kT < m

. One says that the photons were “reheated” be

electron–positron annihilation.

The ratio between the post-annihilation photon and neutrino tempera-

tures can be calculated by using the fact that the electron–positron–photon

system remains in thermal equilibrium until there are very few remaining

electrons and positrons which implies that the post- and pre-annihilation

entropies of this system are equal. The calculation gives

=(4/11)

1/3

. (9.84)

This corresponds to a neutrino number density of

+ n

=(3/11)n

per species . (9.85)

The temperature ratio (9.84) is maintained as long as the neutrinos remain

relativistic since in this case both photon and neutrino temperatures fall as

−1

. If the neutrinos have masses that are suﬃciently small m

 kT

they are still relativistic and have a present temperature of

)=(4/11)

1/3

) ∼ 2K (if m

 10

−4

eV) . (9.86)

On the other hand, the density ratio (9.85) is maintained whether or not the

neutrinos remain relativistic, so today we expect

+ n

=1.12 × 10

−3

per species . (9.87)

9.7 Cosmological nucleosynthesis

At suﬃciently high temperatures and densities, nuclear reactions can take

place and it is important for cosmologists to understand the mix of elements

9.7 Cosmological nucleosynthesis 425

that is produced in the early Universe. The calculations were originally per-

formed by Gamow and collaborators in the 1940s with the hope that the

relative abundances of all elements could be explained. We now know that

nuclear reactions froze at kT ∼ 30 keV leaving most nuclei in the form of hy-

drogen and helium. Nucleosynthesis started up again once stars were formed

providing “gravitational conﬁnement” for astronomical “fusion reactors.”

In this section, we will present a very brief introduction to the theory and

conﬁrming observations [106]. The essential theoretical result will be predic-

tions for the relative abundances of the light elements (A ≤ 7, Table 9.3).

Observationally, it is very diﬃcult to determine the primordial abundances

because of “pollution” by stellar nucleosynthesis. The best observational es-

timates are given in Table 9.3. Apart from

Hand

He, small quantities of

He,

Li were produced in the early Universe.

Table 9.3. The important nuclei for nucleosynthesis with their binding energies

per nucleon, B/A, their observed primordial abundances, their half-lives and decay

modes. (The half-life of

Be by electron capture is given for atomic beryllium.) We

note the high binding energy of

He in comparison with the other light nuclei, which

implies that this species will be the primary product of primordial nucleosynthesis.

The absence of stable nuclei at A =5orA = 8 prevents the production of heavy

elements by two-body reactions between

H and

He. Primordial nucleosynthesis

therefore stops at A = 7. The production of heavy elements occurs in stars where

the triple-α reaction 3

He →

C takes place.

nucleus B/A n

half-life decay mode

(MeV) primordial

(observed)

p01 > 10

n 0 0 10.24 min n → pe

−

H1.11∼ 5 × 10

−5

H 2.83 0 12.3 yr

H →

He e

−

He 2.57 ?

He 7.07 0.08

Li 5.27 0 3 × 10

−22

Li → p

Li 5.33 < 10

−10

Li 5.61 ∼ 3 × 10

−10

Be 5.37 0 53.3 d e

− 7

Be → ν

Be 7.06 0 6.7 × 10

−17

Be →

426 9. Nuclear Cosmology

We will see that the abundances are predicted as a function of the baryon

to photon ratio η. The calculated values agree with the best observations for

η =

∼ 5 × 10

−10

⇒ Ω

ηn

∼ 0.04 . (9.88)

This is an extremely important result since it is signiﬁcantly less than the

estimates of the total matter density Ω

∼ 0.3 implying the existence of

nonbaryonic dark matter.

Calculation of the primordial abundances are performed by numerically

integrating the appropriate Boltzmann equations for each nuclear species.

While this obviously requires a complicated computer code, we can under-

stand things quantitatively because at high temperature most of the nucleons

are free and remain so to a surprisingly low temperature, kT ∼ 70 keV. Most

of the results can be understood by considering three epochs illustrated in

Fig. 9.9:

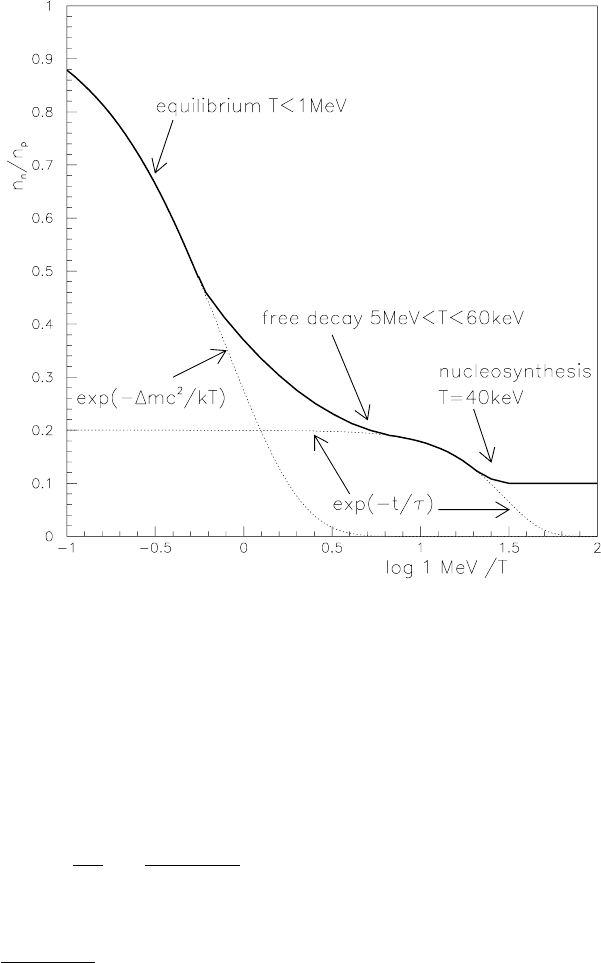
• kT > 800 keV. Neutrons and protons are free and in chemical equilibrium

implying

∼ exp



−

− m



, (9.89)

where (m

− m

=1.29 MeV. The chemical equilibrium is possible

because of reactions transforming neutrons into protons and vice versa:

n ↔ e

−

p ↔ e

n . (9.90)

The cross-sections for these weak reactions are of the same order of mag-

nitude as that for ν

ν ↔ e

−

considered in the previous section so the

reaction rate per baryon is approximately given by (9.83). The equilibrium

is lost when the reaction rates fall below the expansion rate (9.56). The

freeze-out temperature turns out to be kT ∼ 800 keV, similar to that for

νν ↔ e

−

. From (9.89) it follows that the neutron–proton ratio at the

end of this epoch is of order

) ∼ 0.2 kT

∼ 800 keV . (9.91)

• 800 keV >kT >60 keV. The neutrons decay freely. The duration of this

period is ∆t = t(60 keV) −t(800 keV) ∼ 3 min (Exercise 9.5) so about half

the neutrons decay leaving a neutron–proton ratio of

(60 keV) ∼ 0.2exp(−∆t/τ

) ∼ 0.1 . (9.92)

• kT ∼ 60 keV: nucleosynthesis. The remaining neutrons are rapidly incor-

porated into nuclei via a series of reactions, the most important being:

np→

H γ (9.93)

H →

He n

H →

9.7 Cosmological nucleosynthesis 427

Fig. 9.9. The neutron–proton ratio as a function of temperature, as explained in

the text.

H →

He p

H →

He n

H →

He γ .

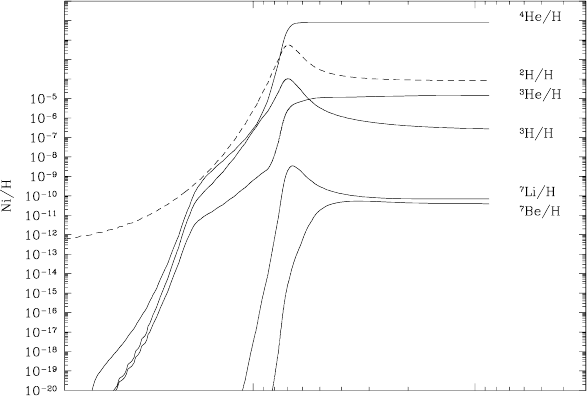
The nuclear abundances versus time are shown in Fig. 9.10. For η ∼ 5 ×

−10

, practically all the neutrons are incorporated into

He, the most

bound light nucleus.

The number of available neutrons (9.92) therefore

determines the quantity of helium:

1 − n

∼ 0.25 (η ∼ 5 × 10

−10

) . (9.94)

There are two obvious questions that we can ask about this scenario: why

does nucleosynthesis start so late (kT ∼ 70 keV) and why does it stop so soon

The most bound nucleus is abundant not because it is easy to produce but rather

because it is very diﬃcult to destroy at kT ∼ 60 keV.

428 9. Nuclear Cosmology

T (MeV)

0.1 0.01

0.0001

0.001

0.01

0.1

Fig. 9.10. The calculated abundances of the light elements as a function of temper-

ature for η =3× 10

−10

as calculated in [104]. The abundances are negligible until

kT ∼ 70 keV, after which most of the available neutrons are incorporated into

He.

After kT ∼ 30 keV, nuclear reactions are frozen and the abundances are constant

in time except for the later decays of

H and

Be. Figure courtesy of Elisabeth

Vangioni-Flam.

without the production of heavy elements. The ﬁrst question is especially

interesting because the nuclear binding energies are all in the MeV range

so it might be expected that nuclei would be produced when T ∼ MeV.

The reason for the late start is the tiny baryon–photon ratio η ∼ 5 × 10

−10

and its eﬀect on the ﬁrst step of nucleosynthesis, the formation of

H via

reaction (9.93). For η ∼ 5 × 10

−10

and for T ∼ MeV the rate per neutron of

this reaction is greater than the expansion rate (Exercise 9.3), from which it

follows that there is approximate chemical equilibrium between n , p and

Under these conditions, the formation rate of

H is equal to the destruction

rate by photo-dissociation:

σ

v

= n

σ

2γ

v

, (9.95)

where n

is the number density of

H. Since n

 n

, (9.95) can be

satisﬁed only if n

 n

to compensate for the large number of photons.

This situation persists until the temperature is suﬃciently low that σ

2γ

v

becomes small because very few photons have energies above the threshold

for photo-dissociation (2.2 MeV). Using the Saha equation, it can be shown

(Exercise 9.3) that n

 n

for kT > 70 keV. Since heavier nuclei cannot

9.7 Cosmological nucleosynthesis 429

be formed until

H is formed, it follows that nucleosynthesis cannot start

until kT ∼ 70 keV.

The end of nucleosynthesis so soon after its start is due to two eﬀects.

The ﬁrst is the absence of stable or metastable elements with A =5or

A = 8 which makes it impossible to form anything from the two primary

species,

He and

H. The second is the increasing eﬃciency of the Coulomb

barrier between charged nuclei which strongly suppresses the cross-sections

for kT < 60 keV. Nuclear reactions therefore freeze-out at a temperature of

kT ∼ 30 keV with a non-equilibrium relic abundance of nuclei characterized

by the complete lack of heavy nuclei.

As we have already mentioned, one of the great interests of the theory of

primordial nucleosynthesis is that a comparison with observations permits us

to estimate η. The predicted abundances as a function of η are shown in Fig.

9.11. The abundance of

He, the primary product of primordial nucleosyn-

thesis, is an increasing function of η. The abundances of the loosely bound

intermediate nuclei

Hand

He are decreasing functions of η. The reason for

this behavior is quite simple. Nucleosynthesis can proceed only if the reac-

tion rates between nuclei are greater than the expansion rate. The nuclear

reaction rates are proportional to densities of initial state nuclei, which are

themselves proportional to the total baryon density. For the ﬁrst reaction

(9.93), it is easy to show (Exercise 9.3) that its rate per neutron is smaller

than the expansion rate for η<10

−13

implying that there is essentially no

nucleosynthesis for η<10

−13

.Forη>10

−13

, nucleosynthesis proceeds with

an eﬃciency that increases with η. More precisely, the temperature of the

nuclear freeze-out is a decreasing function of η. The later the freeze-out, the

more eﬃcient the destruction of the intermediate nuclei and the production

He.

We see in Fig. 9.11 that for η ∼ 5 × 10

−10

the abundance of

He is

rather insensitive to η.Thisissimplybecausethegreatmajorityofthe

available neutrons are incorporated into this nucleus. On the other hand, the

abundance of

H is very dependent on η, so a reliable measurement of the

primordial abundance of

H would yield a robust measurement of η.

It is in principle simple to measure the quantity of

H in intergalac-

ticcloudsbymeasuringtherelativeabsorptionbydeuteriumandhydro-

gen of photons from background objects. The brightest background objects

are quasars, believed to be massive black holes radiating photons as matter

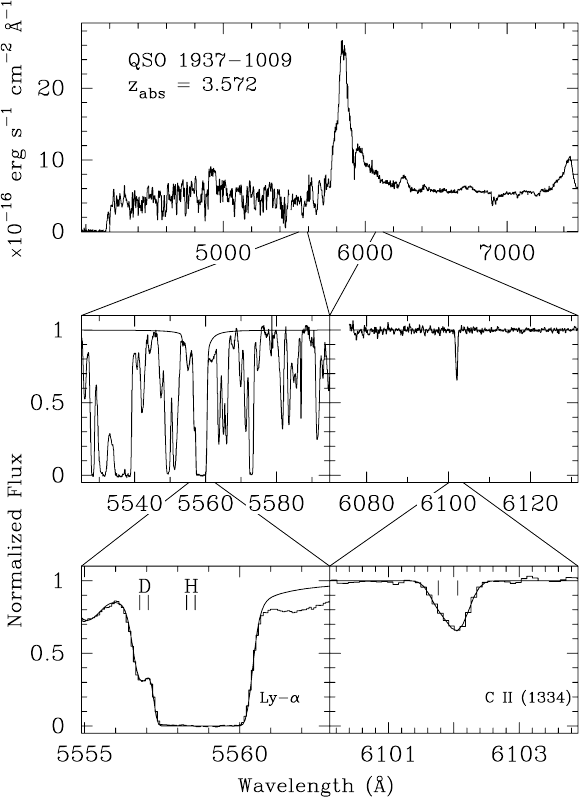
falls into them. Figure 9.12 shows the spectrum of a high-redshift quasar. The

spectrum exhibits a prominent “Lyman-α” emission line corresponding to the

n =2→ n = 1 states of atomic hydrogen, caused by ﬂuorescence of material

surrounding the black hole. The line is at λ = 121 nm but in the spectrum

it is redshifted to 580 nm. Blueward of the quasar’s Lyman-α emission, we

see the forest of lines corresponding to Ly-α absorption in individual clouds

along the line-of-sight. The formation of these absorption lines is illustrated

in Fig. 9.13.

430 9. Nuclear Cosmology

0.0001 0.001 0.01 0.1 1

0.0001

0.001

0.01

0.1

Fig. 9.11. The abundances of the light elements as a function of the assumed

baryon–photon ratio η (Bottom Horizontal Axis) or of the assumed value of Ω

(Top Horizontal Axis), as calculated in [104]. For

He, the abundance is given as

the fraction Y

= ρ

/ρ

of the total baryonic mass that is in the form of

He,

while the other elements are reported as number densities normalized to

H. The

abundance by mass of

He is a slowly increasing function of η. The abundances

of the loosely bound intermediate nuclei

H and

He are decreasing functions of

η. The form of the curve for

Li is due to the fact that the production is mostly

direct for η<3 × 10

−10

and mostly indirect via production and subsequent decay

Be for η>3 × 10

−10

. Observations [105] indicate that

H ∼ 3.4 × 10

−5

high-redshift intergalactic clouds. If this ﬁgure reﬂects the primordial abundance,

we can conclude that η ∼ 5×10

−10

corresponding to Ω

∼ 0.04 (Ω

∼ 0.04). Figure

courtesy of Elisabeth Vangioni-Flam.

9.7 Cosmological nucleosynthesis 431

Fig. 9.12. A quasar spectrum showing Ly-α emission at 580 nm and, blueward of

this line, the “forest” of Ly-α absorption lines by intervening gas clouds [105]. The

zoom on the left shows Ly-α hydrogen and deuterium absorption by one cloud.

The

H line is shifted with respect to the hydrogen line because the atomic energy

levels are proportional to the reduced electron–nucleus mass. The ratio between the

hydrogen and deuterium absorption can be used to determine the two abundances

within the cloud. Courtesy of D. Tytler.

432 9. Nuclear Cosmology

1+z

observer z=0

quasar zq

Fig. 9.13. The formation of absorption lines in quasar spectra by intervening clouds

of intergalactic gas. The emission at λ

corresponding to the n =2→ n = 1 line

of atomic hydrogen (right) is observed to be redshifted to λ

/(1 + z

) (left). The

observed spectrum also shows absorption in the cloud at λ

/(1 + z

) corresponding

to the inverse transition, n =1→ n =2.

The amount of absorption is determined by the quantity of hydrogen in

the cloud. The trick is to ﬁnd a cloud that has an optical depth that per-

mits the observation of absorption by both hydrogen and deuterium. Such

a cloud appears in the spectrum with absorption at 555.8 nm for hydrogen.

The absorption is total at the center of the hydrogen line but the quantity

of hydrogen in the cloud can be estimated from the width of the absorption

proﬁle. Also visible is the deuterium absorption line and the quantity of deu-

terium can be estimated from the total absorption at this line. The spectrum

shows that only clouds within a narrow range of optical depth can be used to

measure the deuterium–hydrogen ratio. The measurement would be impos-

sible for clouds with less absorption (making the deuterium line too weak to

be observed) or for clouds with more absorption (causing the hydrogen line

to widen into the deuterium line).

Only a handful of appropriate absorption systems have been found in

quasar spectra. The three best examples give results that are consistent with

[105]:

=(3.4 ± 0.3) × 10

−5

. (9.96)

The quantity of heavy elements in the three high-redshift clouds is very

small (∼ 10

−3

solar abundance) which suggests that the

H abundance might

be unperturbed by stellar nucleosynthesis. If we suppose that (9.96) reﬂects

the primordial abundance, the theory of nucleosynthesis gives a precise value

of η and Ω

η ∼ (5.1 ± 0.3) × 10

−10

⇒ Ω

=0.039 ± 0.002 . (9.97)

As is often the case in astrophysics, the cited error is purely formal be-

cause the real uncertainty comes from the hypotheses necessary to interpret