Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

9.3 Gravitation and the Friedmann equation 413

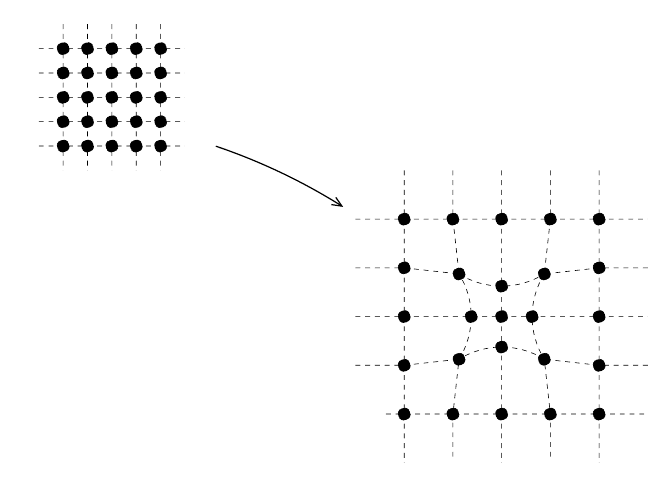
We also note that the equations of general relativity for a homogeneous

Universe will be simple because the coordinate grid can be described by one

function a(t). In an inhomogeneous Universe, the situation is much more

complicated, as illustrated in Fig. 9.5. In the ﬁgure we have supposed that

there is an excess of mass in the center of the ﬁgure. The gravitational at-

traction of matter to this excess will cause the test particles to expand in

a non-uniform manner. Even if the coordinate system is simple at the be-

ginning, it will evolve into a complicated system with distances between test

particles deﬁned by three metric functions

==g

(t, x, y)dx

+ g

(t, x, y)dxdy + g

(t, x, y)dy

. (9.46)

We now have 3 functions of position and time to describe the coordinate

system. The three functions g

, g

and g

deﬁne the (spatial) metric of

the coordinate system. The equations that govern the metric can be quite

complicated.

=dx +dy

+gdxdy

+2g

Fig. 9.5. Same as Fig. 9.4 but with a mass excess near the center of the region.

The excess gravity causes the test particles to separate less rapidly near the center

than in the homogeneous case. The resulting formula for dS is more complicated.

Fortunately for us, the metric of a homogeneous Universe is described by

only one function a(t) and we can expect the Einstein equation to be simple.

It turns out to be

414 9. Nuclear Cosmology

¨a

−4πG

(ρ +3p) , (9.47)

where ρ is the energy density and p is the “pressure.” As expected, a positive

energy density ρ>0 works to decelerate the Universe. In fact, the part of the

r.h.s. that is proportional to ρ can be guessed through a simple Newtonian

argument, as shown in Exercise 9.4. On the other hand, the appearance of

a correction proportional to the pressure p is surprising, especially since a

positive pressure also works to decelerate the Universe, out of line with our

intuition of thermal pressure encouraging the expansion of a gas. This is

however not the role of the pressure in the gravitational context where it acts

as a source of gravitation that is normally ignored in Newtonian problems.

To see why it can often be ignored, we note that for a collection of particles

(number density n), the pressure can be deﬁned to be proportional to the

mean value of |p|

/3E:

p ≡ n|p|

/3E . (9.48)

For instance, for a thermal collection of nonrelativistic particles of mass m,

the energy density is ρ = mc

n and the pressure is given by

p = n(|p|c)

/3E = nkT , (9.49)

wherewehaveused|p|

/2m =(3/2)kT. This value of the pressure is just

that of the ideal gas law. Because kT  mc

for a non-relativistic gas, this

shows that the relativistic correction is small. On the other hand, for a rela-

tivistic gas (|p|c ∼ E)wehave

p = n(|p|c)

/3E = ρ/3 . (9.50)

An example of such a gas is the cosmic (photon) background radiation. For

such a gas, the relativistic correction proportional to the pressure is large and

doubles the deceleration rate.

In an adiabatic expansion, the volume and energy of a gas change accord-

ingtothelawdE = −pdV . This suggests that in a cosmological context the

pressure can be deﬁned by the way that the energy density changes as the

Universe expands:

p = −

dρa

. (9.51)

Using the laws (9.39) and (9.40) for the evolution of the energy density, we

see that (9.51) implies that, as expected, p = 0 for a non-relativistic gas and

p = ρ/3 for a relativistic gas. On the other hand, the fact that the vacuum

energy density is constant (9.41) implies that for vacuum energy we have

p = −ρ vacuum . (9.52)

A negative pressure is perhaps counter intuitive but we should not forget that

our intuition for pressure is based on the pressure of collections of particles

whereas the vacuum is the absence of particles.

9.3 Gravitation and the Friedmann equation 415

The solution ˙a(t) of (9.47)with the pressure (9.51) is

˙a



8πGρ



+const.

To evaluate the constant we use the present values ˙a(t

)=H

and

8πGρ(t

)/3c

= H

Ω

to ﬁnd

˙a

8πGρa

+ H

(1 − Ω

) . (9.53)

Dividing (9.53) by a

we ﬁnd the “Friedmann equation”:



˙a



8πGρ

+ H

(1 − Ω

)





. (9.54)

We note that the measurement previously discussed of the Cosmic Back-

ground Radiation anisotropies indicate Ω

∼ 1 so that the second term on

the r.h.s. nearly vanishes. At any rate, it can be ignored in the primordial

Universe since it diverges as a

−2

whereas the radiation density diverges as

−4

We will be mostly interested in the expansion rate in the primordial Uni-

verse when the energy density and pressure were dominated by relativistic

radiation given by the Stefan–Boltzmann law:

ρ(T )=g(T )

(kT)

(¯hc)

, (9.55)

where g(T ) is the eﬀective number of relativistic spin degrees of freedom in

thermal equilibrium at the temperature T (g = 2 for a blackbody photon

gas). At T = 1 MeV, photons, three neutrino species and electron–positron

pairs are in equilibrium corresponding to g(kT =1MeV)∼ 10.75. (Note

that a fermion degree of freedom counts for only ∆g =7/8 because the Pauli

principles restricts the number of fermions.) When nucleosynthesis occurs at

kT ∼ 50 keV, only photons and neutrinos [with T

∼ (4/11)

1/3

] are present

giving g(kT =50keV)∼ 3.36.

We then have

˙a



8πG

g(T )

(kT)

(¯hc)



1/2

∼ 0.65 s

−1



1MeV





g(T )



1/2

. (9.56)

The Hubble time, i.e. the time for signiﬁcant changes in the temperature is

the inverse of ˙a/a. It is about 1 sec for T ∼ 1 MeV and about 100 sec for

kT ∼ 100 keV when nucleosynthesis begins.

416 9. Nuclear Cosmology

9.4 High-redshift supernovae and the vacuum energy

The general relativistic equation (9.47) combined with the surprising nega-

tive pressure for a positive vacuum energy (9.52) means that the expansion

accelerates in a Universe dominated by vacuum energy:

¨a

8πG

if ρ

tot

∼ ρ

. (9.57)

The observational evidence for acceleration involves the observed photon ﬂux

from high redshift supernovae.

Understanding the relation between the measured ﬂux of a supernova and

its redshift requires the use of general relativity. However, we can understand

the relationship qualitatively through the following argument. The ﬂux is

determined by the present distance R to the supernova

φ ∝

∼

− t

)

, (9.58)

where in the second form we replace the distance by the ﬂight time c(t

−t

)

where t

and t

are the explosion and detection times.

On the other hand, the redshift, z, is deﬁned by the emitted (λ

)and

observed (λ

) wavelengths of photons

1+z ≡

. (9.59)

For nearby objects, this redshift is most simply interpreted as a Doppler shift

(9.27). However, equation (9.35) tells us that more generally the redshift is

the universal expansion factor between the time of the explosion and the time

of the observation

1+z =

a(t

)

a(t

)

. (9.60)

If the expansion is accelerating (decelerating), the expansion rate in the

past was relatively slower (faster) implying a longer (shorter) time between

the explosion and observation. Equation (9.58) then implies that in an ac-

celerating (decelerating) Universe, a ﬁxed redshift therefore corresponds to a

relatively small (large) photon ﬂux.

Two teams [95, 96] have observed that the ﬂuxes of supernova at z ∼ 0.5

are about 40% smaller than that expected for a decelerated Universe of mass

density equal to the critical density. The eﬀect can be explained by a vacuum

energy Ω

∼ 0.7.

9.5 Reaction rates in the early Universe

These days, not much goes on in intergalactic space. There are no nuclear

reactions occurring and photons and neutrinos very rarely scatter on matter.

9.5 Reaction rates in the early Universe 417

More quantitatively, the number of reactions per particle per unit time, λ,

is much less than one reaction per Hubble time. For example the rate of

Compton scattering per photon is

γe→γe

= n

c ∼ 1.4 × 10

−3

, (9.61)

where the free electron density is set equal to the baryon density from Table

9.1 and σ

is the Thomson cross-section. The numerical value in the second

form means that only one photon out of 700 will scatter in the next Hubble

time. As long as the Universe continues to expand, reactions will become

rarer and rarer as the density decreases. In fact, we will see that the typical

photon will never scatter again.

Things were quite diﬀerent in the early Universe. Just before electrons

and nuclei recombined to form atoms, the temperature was 1000 times its

present value so the density of electrons was 10

times the present den-

sity. The expansion rate, given by the Friedmann equation (9.54), was only

√

Ω

1000

3/2

∼ 2 × 10

times the present rate:

γe→γe

rec

) ∼ n

rec

) σ

c ∼ 80 H(t

rec

) . (9.62)

At this epoch, a typical photon suﬀered 80 collisions per Hubble time.

The thermal spectrum of photons resulted from the high reaction rate in

the early Universe. Elastic scattering, e.g.

γ e

−

↔ γ e

−

, (9.63)

caused energy exchanges between particles and generated “kinetic” equilib-

rium, i.e. a thermal momentum distribution. Inelastic collisions changed the

number of particles and generated “chemical” equilibrium where the parti-

cle densities have thermal values. For example, bremsstrahlung and photon

absorption

−

p ↔ e

−

pγ , (9.64)

creates and destroys photons, generating a thermal number density

2.4

(kT)

(¯hc)

(9.65)

The elementary reactions

γγ ↔ e

−

↔ ν

ν (9.66)

generated thermal (blackbody) densities of electron–positron pairs and neu-

trinos:

= n

−

= n

+ n

=(3/4)n

kT  m

. (9.67)

The factor (3/4) comes from the fact that fermions must respect the Pauli

principle and, as such, have smaller numbers in thermal equilibrium. Also

important are the neutron–proton transitions:

n ↔ e

−

p ↔ e

n . (9.68)

418 9. Nuclear Cosmology

These reactions established chemical equilibrium between protons and neu-

trons (4.35):

=exp



−(m

− m



kT > 1MeV . (9.69)

This determines the number of neutrons available for nucleosynthesis.

The minimal requirement for the establishment of thermal equilibrium is

that the reaction rate per particle be greater than the expansion rate:

λ 

˙a

⇒ thermal equilibrium . (9.70)

The expansion rate is the relevant parameter because its inverse, the Hubble

time t

, gives the characteristic time for temperature and density changes

due to the universal expansion. Collisions can therefore perform the necessary

readjustments of momentum and chemical distributions only if each particle

reacts at least once per Hubble time.

Because of the expansion, the collision epoch was bound to end when the

reaction rate became less than the expansion rate, λ  ˙a/a.Whathappens

to the thermal distributions once the collisions cease depends on the type of

equilibrium. For purely kinetic equilibrium, i.e. the momentum spectrum of

particles, the thermal character of the spectrum may be maintained by the

expansion. This is the case for the CBR photons.

On the other hand, chemical thermal equilibrium is maintained only by

reactions and the equilibrium is lost once the reactions cease. At the present

low temperature, chemical equilibrium would imply that nucleons would tend

to be in their most bound states near

Fe.Thisisnotthecasebecausethe

nuclear reactions necessary to reach this state ceased when the temperature

was much higher, kT ∼ 30 keV. Most nucleons were thus “stranded” in hydro-

gen and helium. We say that the nuclear reactions “froze” at a temperature

∼ 30, keV. The “freeze-out” left the Universe with a “relic” density of

hydrogen and helium nuclei that is far from the equilibrium density.

The nuclear freeze-out left the Universe with a reserve of free energy,

i.e. energy that can now be degraded by entropy producing (exothermic)

nuclear fusion reactions. In particular, hydrogen can be converted to helium

and helium to heavier elements once matter is gravitationally conﬁned in

stars. Fusion reactions in stellar interiors transform mass into kinetic energy

of the reaction products which is then degraded to thermal energy including

a multitude of thermal photons. It is this increase in the number of photons

which is primarily responsible for the entropy increase.

After the photons escape from a star, entropy production can continue

if the photons are intercepted by a cold planetary surface. On Earth, solar

photons (T ∼ 6000 K) are multiplied into ∼ 20 thermal photons (T ∼ 300 K).

The accompanying entropy increase more than compensates for the entropy

decrease associated with the organization of life induced by photosynthesis.

Entropy is always approximately proportional to the number of particles.

9.5 Reaction rates in the early Universe 419

Without the thermal gradient between the Sun and Earth photosynthesis

would not be possible because of the second law of thermodynamics. We see

that the loss of thermal nuclear equilibrium in the early Universe provides the

free energy necessary for life on Earth. Without this energy source, life would

depend on the photons produced during the contraction phases of stars (Fig.

8.3).

The explanation for the current thermal disequilibrium is one of the great-

est triumphs of modern cosmology. Nineteenth century physicists were puz-

zled by the disequilibrium because they knew that all isolated systems tend

toward thermal equilibrium. They also worried about the future “heat death”

of the Universe when equilibrium will be reached, terminating all intelligent

activity. Modern cosmology appears to have inverted the sequence of events

since the state of thermal equilibrium occurred in the past rather than the

future.

It should be noted, however, that the early Universe can be said to have

been in thermal equilibrium only if we ignore the possibility of gravitational

collapse of inhomogeneities. Gravitational collapse results in the radiation of

photons (Sect. 8.1.1) and this process generates entropy. The initial homo-

geneous (and therefore low entropy) conditions of the Universe are therefore

“special” and require an explanation as to how they were established.

In order to establish the formalism for the study of reactions in an ex-

panding Universe, we consider a general two-body reaction

ij → kl (9.71)

In Sect. 3.1.4 we saw that the reaction rate per particle i is proportional to

the number of j particles present and to the cross-section times velocity:

ij→kl

≡ n

σ

ij→kl

v . (9.72)

We note that λ

ij→kl

= λ

ji→kl

. This is simply because the reaction rate per

particle i is proportional to the number of particles j and vice versa.

The Boltzmann equation governing the time dependence of n

was derived

in Chap. 3 for a time-independent volume (3.32). For an expanding Universe,

the equation is modiﬁed to include the eﬀect of the expansion:

= −3

˙a

− n

ij→kl

+ n

kl→ij

. (9.73)

The three terms in this equation describe the three eﬀects that change n

the expansion of the Universe, destruction of i particles, and creation of i

particles.

While there is no analytic solution to the Boltzmann equation, there are

two very simple limits with approximate solutions. The ﬁrst is if the expansion

rate is much greater than the destruction rate, ˙a/a  λ

ij→kl

, and production

rate ˙a/a  (n

)λ

kl→ij

. In this case the ﬁrst term dominates

= −3

˙a

⇒ n

∝ a

−3

. (9.74)

420 9. Nuclear Cosmology

As expected, the number density of i particles just dilutes with the expansion

of the Universe.

The second case occurs if the reaction rates are much greater than the

expansion rates, the Boltzmann equation is simply that for a gas of particles

in a ﬁxed volume

= − n

ij→kl

+ n

kl→ij

⇒ n

∼ n

(T ) . (9.75)

The solution in this case is the thermal equilibrium solution (principle of

detailed balance). This comes about since if n

is greater than (less than)

the equilibrium value, the ﬁrst term (second term) dominates and the time

derivative of n

is negative (positive). The equation then pushes n

to the

equilibrium value where the two terms cancel. The slow time dependence

due to the temperature decrease with the expansion is then enforced by the

ﬁrst term of (9.73).

We can therefore get a qualitative understanding of the solution of the

Boltzmann equation by simply comparing expansion and reaction rates. De-

pending on which is greater, we will either have free dilution or thermal

equilibrium. This will be our strategy in the following sections.

9.6 Electrons, positrons and neutrinos

As a ﬁrst application of the Boltzmann equation, we will treat the case of

electrons and positrons. These particles are created and destroyed principally

by the reaction

−

↔ γγ . (9.76)

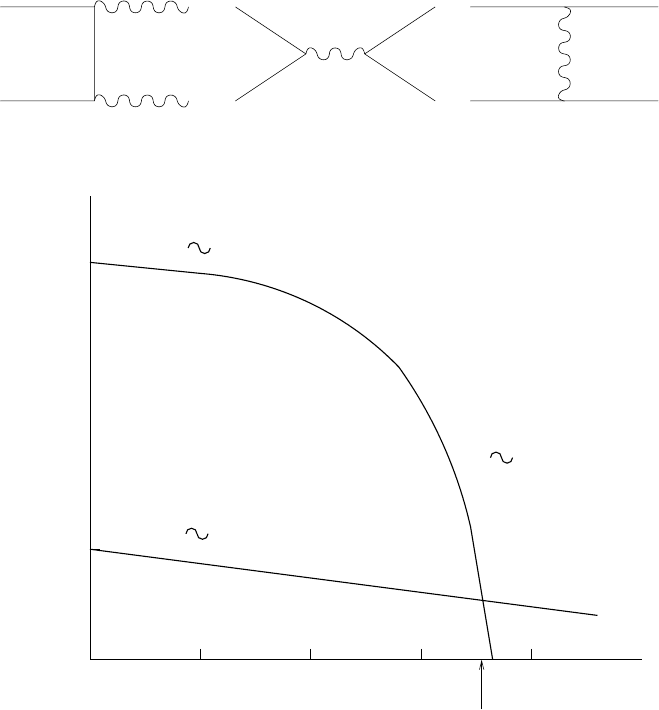
The diagram is shown in Fig. 9.6. For high center-of-mass energies, E



, the annihilation cross-section is

−

→γγ

=(¯hc)

2πα

[2ln(E

) − 1] E

 m

. (9.77)

For low energy, v  c, the cross-section is proportional to 1/v as is expected

for barrier-free exothermic reactions:

−

→γγ





=(¯hc)

πα

v  c. (9.78)

To determine if the electrons and positrons are in chemical equilibrium

with the photons, we only need to calculate the thermal equilibrium value

of the annihilation rate and compare it with the expansion rate given by the

Friedmann equation (9.56). The expansion and annihilation rates are shown

in Fig. 9.7. For the annihilation rate, there are two simple limits, kT  m

and kT  m

For kT  m

,wesimplyreplaceE

in (9.77) with its mean value ∼ kT

so σv∝T

−2

(ignoring the logarithmic factor). The densities of electrons

9.6 Electrons, positrons and neutrinos 421

Fig. 9.6. The diagrams for the reactions e

−

↔ γγ and ν

ν ↔ e

−

−m

/kT

−2

−1

Γlog (T)

110100

log H

kT / m

Fig. 9.7. The annihilation rate λ(e

−

→ γγ) and the expansion rate H =˙a/a

as a function of temperature under conditions of thermal equilibrium and with

−

= n

.ForT>T

, λ> ˙a/a and n

will take its equilibrium value. For

T<T

, λ< ˙a/a and the reactions are “frozen.” After the freeze-out, the number

of electrons and positrons is constant so n

decreases as 1/a

422 9. Nuclear Cosmology

and positrons are proportional to T

and the annihilation rate is therefore

proportional to the temperature:

−

→γγ

∼ ¯h

−1

kT ∼ 10

−1



1MeV



kT  m

, (9.79)

where we have suppressed the numerical prefactors. Comparing (9.56) and

(9.79), we see that λ>˙a/a for kT < 10

GeV. For example, at kT ∼ m

λ ∼ 10

˙a/a, i.e. 10

reactions per Hubble time. We can conclude that the

electrons and positrons were in chemical equilibrium with the photons for

<T <10

GeV.

The equilibrium is inevitably lost for T  m

because, for a Universe

with equal numbers of electrons and positrons, the equilibrium density falls

rapidly with an exponential Boltzmann factor (Exercise 9.6):

−

= n

∝ exp(−m

/kT ) m

 kT . (9.80)

The annihilation rate drops accordingly and one ﬁnds numerically that it falls

below the expansion rate when kT ∼ m

/40 when the electron–photon ratio

is ∼ 2 × 10

−16

. The temperature at which this occurs is called the “freeze-

out” temperature T

because after this temperature is reached the number of

electrons and positrons is frozen.

Figure 9.8a shows the ratio between the number of electrons and the

number of photons as a function of temperature calculated by numerically

integrating the Boltzmann equation. For T  T

the electron–photon ratio

is ﬁxed at about ∼ 2 × 10

−16

, conﬁrming our qualitative argument.

The evolution of n

−

and n

for a universe like our own with an excess

of electrons over positrons is shown in Fig. 9.8b. The electron excess coupled

with charge conservation leads to a small number of electrons surviving the

primordial epoch.

The evolution of the neutrino density is governed by the same principles

as that of the electron–positron density. The three neutrino species can be

produced and destroyed at kT ∼ MeV by the reaction (Fig. 9.6)

ν ↔ e

−

. (9.81)

Since this reaction is due to the weak interactions, the cross-section for all

species is of order

σ ∼

(¯hc)

 E

 m

. (9.82)

The annihilation rate is therefore

ν→e

−

= n

σv∼

(kT)

¯h(¯hc)

∼ 1s

−1



1MeV



 kT , (9.83)