Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

8.4 Nuclear astronomy 393

1000

1200

1400

1600

−20

E (keV)

820

840

860

880

−4

−2

E (keV)

photons cmflux (10

−

keV

−

)

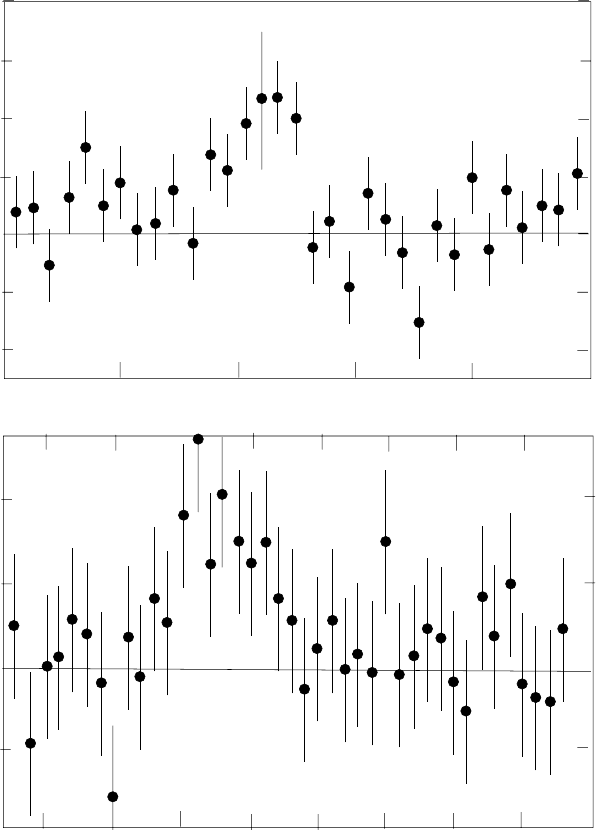
Fig. 8.18. γ-ray spectra from supernova remnants. The top panel shows the 847 keV

line (

Co) from SN1987A [90]. The bottom panel shows the 1157 keV line (

Ti)

from the region Cas A [91]. This region is believed to be the remnant of a supernova

that exploded about 300 years ago.

394 8. Nuclear Astrophysics

Table 8.2. Radioactive nuclei giving rise to observable γ-rays. β-emitters with

511 keV annihilation radiation are labeled with e

Decay t

1/2

sites

(keV)

Ni →

Co 6.077 day 158, 269, 480 supernovae

Co →

Fe 77.27 day 847, 1238, e

supernovae

Ni →

Co 35.60 hr 127, 1377, 1919 supernovae

Co →

Fe 271.79 day 14, 122, 136 supernovae

Ti →

Sc 63 yr 68, 78, e

supernovae

Sc →

Ca 3.927 hr 1157, e

supernovae

Fe →

Co 1.5 × 10

yr supernovae, WR, AGB

Co →

Ni 5.2714 yr 1173, 1332 supernovae, WR, AGB

Al →

Mg 7.17 × 10

yr 1160 supernovae, novae,

WR,AGB

Be →

Li 53.12 day 478 novae

Na →

Ne 2.6019 yr e

, 1274 novae

Bibliography

1. H. Karttunen, P. Kr¨uger,H.Oja,M.Poutanen,K.Donner,Fundamental

Astronomy, Springer, Berlin, 2003.

2. Hansen, Carl J., Kawaler, Steven D., Trimble, Virginia, Stellar Interiors

Springer, Berlin, 2004.

3. D. D. Clayton, Principles of Stellar Evolution and Nucleosynthesis

,Uni-

versity of Chicago Press, Chicago, 1983.

4. B. E. J. Pagel, Nucleosynthesis and Chemical Evolution of Galaxies

Cambridge University Press, Cambridge, 1997.

5. J. Audouze and S. Vauclair, An introduction to nuclear Astrophysics

Reidel, 1980.

6. D. Arnett, Supernovae and Nucleosynthesis

, Princeton University Press,

Princeton, 1996.

Exercises

8.1 Find a relation between the stellar temperature and density gradients

assuming that they are due to adiabatic convection of material between lower

Exercises for Chapter 8 395

and higher regions. Show that the photon–baryon density (∝ T

/ρ) is propor-

tional to ρ, consistent with Fig. 8.2 in the outer convective zone, r>0.7R



8.2 Poincar´e gave the following proof of the virial theorem, in the absence

of radiation pressure. Consider a self-gravitating system of N particles whose

potentialenergyis

φ = −G



i=1



j=i+1

− r

where G is Newton’s constant. We denote by E

the sum of kinetic energies

of the N particles.

The moment of inertia of this system with respect to its center of gravity,

which we take as the origin of coordinates is I =



) . Assuming that

the second derivative of I is zero, which is the case for quiet stars such as the

sun, prove that one has

+ φ = 0 hence E = −E

8.3 Calculate the energy liberated in the transformation of carbon and

oxygen to

Ni in a white dwarf of mass 10

. Compare this to the gravi-

tational binding energy of the white dwarf.

8.4 Estimate the time of a neutrino of energy 10 MeV to escape from a

neutron star.

8.5 The fundamental reaction in the sun can be written globally as

4p + 2e

−

→

He + 2

. (8.98)

The binding energy of

He is −28.30 MeV. What is the energy release in this

reaction?

The total luminosity of the sun is L

=410

kW. How many protons

are consumed per second by the reaction (1)?

In its present phase, since it was formed, the sun burns quietly with a

constant luminosity. Its mass is M =210

kg, 75% of which was initially

hydrogen and 25% helium. Only 15% of the hydrogen can actually be burnt

in the reaction (1) in the solar core. For what length of time T can the sun

burn before it becomes a red giant?

8.6 The binding energy of

He is 7.72 MeV. Is the reaction pd →

He + γ

exothermic? Is the inverse reaction possible in the core of a star like the sun?

(The mean photon blackbody energy is ∼ 2.7kT with kT ∼ 1keV.)

396 8. Nuclear Astrophysics

8.7 Consider a completely degenerate fermion gas. What is the equation of

state P (n, T ) of the gas in, respectively, the non-relativistic and the rela-

tivistic regimes. We call kT

the maximum energy of these fermions (T

the Fermi temperature), and p

their maximum momentum. What does the

limit T  T

correspond to? What is the corresponding pressure? Compare

this pressure with the pressure of an ideal gas for a density n ∼ 10

−3

and a temperature T ∼ 10

K (for the ideal gas).

We recall the virial theorem which relates the total internal energy U of a

star to its gravitational energy U

= −αGM

/R with α ∼ 1. A star is formed

by gravitational contraction of a mass M of gas. How does the temperature

of an ideal gas evolve during that collapse? What happens when T ≥ 10

(We recall that the mean temperature of the sun given by the virial theorem

is  2 × 10

K.)

Show that there exists a maximum temperature T

max

in the contraction

if one takes into account the possibility that the electron gas becomes de-

generate. Show that the electron gas becomes degenerate long before the ion

gas, so that the latter can be considered as an ideal gas.

If T

max

≤ 10

K, the star is called a brown dwarf. What is the peculiarity

of such stars? What is the minimum mass of a star that does not become a

brown dwarf?

How is the gravitational stability of a planet ensured? What is the diﬀer-

ence between a planet and a brown dwarf?

8.8 In a massive star at the end of its life, the fusion

Si →

Fe takes place

in a shell around an iron core. The core is degenerate. What happens when

the mass of the core increases because of the Si fusion?

What is the order of magnitude of the Fermi energy of electrons at the

beginning of the collapse? In what follows, we shall use



 3MeV(ρ/10

gcm

−3

) (8.99)

and ρ ∼ 10

gcm

−3

) initially. If the electron capture reactions e

−

+(A, Z) →

(A, Z −1) + ν

are endothermic with Q ∼ a few MeV, why do these reactions

take place when ρ ≥ 10

gcm

−3

? Why don’t the inverse reactions take place?

Neutrinos interact with heavy nuclei in the core with a cross-section of

σ ∼ 10

−42

/1MeV)

The radius of the core evolves as R ∼ 100 km (ρ/10

gcm

−3

)

−1/3

(M/M



)

1/3

Show that the neutrinos produced are trapped when ρ ≥ 10

gcm

−3

The diﬀusion time of neutrinos up to the “neutrinosphere ,” i.e. the region

where neutrinos cease to be coupled to matter is of the order of 1 − 10 sec.

The temperature of the emitted neutrinos is T ∼ 5 MeV. Calculate the

total energy E

tot

carried away by the neutrinos, assuming neutronization is

complete.

Assuming that the collapse ceases at a density of ρ ∼ 10

gcm

−3

, calcu-

late the gravitational energy which is liberated, and compare it with E

tot

9. Nuclear Cosmology

As discussed in the previous chapter, natural nuclear reactions are now mostly

conﬁned to stellar interiors. In the distant past, nuclear reactions are believed

to have occurred throughout the Universe during the ﬁrst few minutes af-

ter the “Big Bang.” At this time the Universe was suﬃciently hot that the

Coulomb barrier could not prevent the fusion of nuclei.

We believe that the Universe went through such a hot epoch because

the Universe is now expanding. By this we mean that the distances between

galaxies are observed to be increasing with time. Speciﬁcally, galaxies are

observed to recede from us with a recession velocity, v, proportional to their

distance R:

v = H

= (70 ±4)(km s

−1

)Mpc

−1

, (9.1)

where we use the conventional astronomic distance unit, 1 pc = 3.085 ×

m. If the galactic velocities were constant in time, this would imply that

all galaxies were superimposed and the cosmological density inﬁnite at a time

inthepastgivenbytheHubbletime

≡ H

−1

=1.4 × 10

yr . (9.2)

Gravitational forces would be expected to make the galactic velocities time-

dependent but the Hubble time nevertheless gives the order of magnitude of

what one calculates for the age of the Universe if the known laws of physics are

used to extrapolate into the past. We do not know if such an extrapolation to

inﬁnite density is justiﬁed but we can say with conﬁdence that the expansion

has been proceeding at least since an epoch when the density was 45 orders

of magnitude greater than at present, with a temperature of kT > 1GeV.

Going backward in time, we would see stars and galaxies melt into a uniform

plasma of elementary particles.

Under such conditions, reactions between elementary particles and nu-

clei took place until the Universal expansion caused the temperature to drop

to a level where the reactions cease because of the decreasing density and

increasing eﬃciency of the Coulomb barrier. It is believed the period of reac-

tions lasted about 3 minutes, ending when the Universe had a temperature

of kT ∼ 40 keV and leaving a mixture of 75%

H and 25%

He (by mass).

This mixture provided the initial conditions for stellar nucleosynthesis that

started once stars were formed some millions of years later.

398 9. Nuclear Cosmology

The job of primordial cosmology is to understand how this process pro-

ceeded from the earliest possible moments. While we cannot say what existed

at “the beginning” (if there was a beginning), we can extrapolate backward in

time to temperatures of order 1 GeV when the Universe was believed to con-

sist of a thermal plasma of relativistic quarks, antiquarks, gluons, neutrinos

and photons. When the temperature dropped below a transition temperature

estimated to be kT ∼ 200 MeV, the quarks and antiquarks combined to form

bound hadrons (mostly pions) which then, for the most part, annihilated

leaving nothing but photons and neutrinos. If there had been equal num-

bers of quarks and antiquarks this would have been pretty much the end of

the story. However, the small excess of order 10

−9

of quarks over antiquarks

meant that a small number nucleons remained at T ∼ 100 MeV, of order

−9

with respect to the photons and neutrinos. This was the initial condi-

tion for cosmological nucleosynthesis that came about when some nucleons

later combined (kT ∼ 40 keV) to form nuclei.

The process of cosmological nucleosynthesis diﬀers from that of stellar

nucleosynthesis in several important respects. Among them are

• The presence of neutrons. Because of the lack of neutrons in stars, stellar

nucleosynthesis must start with the weak reaction 2

H →

.Cosmo-

logical nucleosynthesis starts with an abundant supply of neutrons which

need only combine with protons to form nuclei, starting with the reaction

np→

Hγ.

• A low baryon–photon ratio. Whereas the baryon to photon ratio in stars

is greater than unity (∼ 10

for the sun, Fig. 8.2), it is of order 5 ×10

−9

the primordial Universe. This has the important consequence of delaying

nucleosynthesis since the abundant photons quickly dissociate any nuclei

that are produced until the temperature drops to ∼ 100 keV at which

point the probability of a thermal photon having suﬃcient energy to break

a nucleus becomes small enough.

• A low baryon–neutrino ratio, nearly equal to the baryon–photon ratio.

This was important during the time when most nucleons were free since

weak reactions like ν

n ↔ e

−

p can change neutrons into protons and vice

versa. In fact, for kT > 800 keV it turns out that these reactions are suf-

ﬁciently rapid that they can maintain a “chemical” equilibrium between

the neutrons and protons so that the neutron to proton ration takes the

thermal value of exp(−(m

−m

/kT ). The weak interaction rate drops

to negligible values at a temperature of around 800 keV when the neutron

to proton ratio is about 0.2. Free neutron decay then lowers the ratio to

about 0.1 when nucleosynthesis starts at kT ∼ 100 keV. The proton excess

results in a large quantity of post-nucleosynthesis

• A limited amount of time. The elapsed time from the quark–gluon phase

transition to the end of cosmological nucleosynthesis is about three min-

utes. Below temperatures of ∼ 60 keV, the Coulomb barrier prevents fur-

9.1 The Universe today 399

ther reactions, leaving the primordial mixture of 75% hydrogen and 25%

He.

In this chapter we provide a basic introduction to this process. Section 9.1

summarizes what is believed to be the present state of the observable Universe

and sec. 9.2 discusses how this state evolves as the Universe expands. Section

9.3 shows how the universal expansion is governed by gravity. Section 9.5

discusses the basic physics that governs the particle and nuclear reactions

in the primordial Universe and the following sections apply this physics to

electrons, neutrons, nuclei and some more speculative elementary particles

that may have played an important role in cosmology.

9.1TheUniversetoday

When averaged over large volumes containing many galaxies, the observable

Universe is believed to have the following characteristics:

• Atinydensity,ρ ∼ 10

−26

kg m

−3

, and starlight output, J ∼ 10

−39

−3

;

• A curious “chemical” composition (Table 9.1) with most particles being

cold photons or neutrinos and most mass being in the form of ordinary

“baryonic” matter (protons and nuclei plus electrons), and not-so-ordinary

“cold dark matter” (CDM). Most of the energy is in the form of an eﬀective

vacuum energy or, equivalently, a cosmological constant.

• A non-equilibrium thermal state characterized by a deﬁcit of highly-bound

heavy nuclei.

• A hierarchy of gravitationally bound structures ranging from planets and

stars to galaxies and clusters of galaxies.

In this section, we will review the major components of the Universe listed

in Table 9.1. It will be convenient to express the mean densities in units of

the “critical density”

8πG

(9.3)

where H

is the “Hubble constant”

= (70 ± 4)km sec

−1

Mpc

−1

(9.4)

The physical signiﬁcance of the critical density and the Hubble constant will

be discussed in the next section but here we note only the very low value of

=0.92 h

× 10

−26

kg m

−3

(9.5)

=1.4 h

× 10



Mpc

−3

=0.51 h

× 10

eV m

−3

. (9.6)

where the reduced Hubble constant is h

= H

/70 km sec

−1

Mpc

−1

400 9. Nuclear Cosmology

Table 9.1. The known and suspected occupants of the Universe. For each species,

i, the table gives estimated number density of particles, n

, and the estimated

mass or energy density, Ω

= ρ

/ρ

, normalized to the “critical density,” ρ

(0.92 ±0.08)×10

−26

kg m

−3

. Other than the photon density taken from the COBE

data [92], the numbers are taken from the global ﬁt of cosmological parameters by

the WMAP collaboration [94]. The lower limit on the neutrino density comes from

the oscillation data of [49].

species n

−3

) Ω

= ρ

/ρ

γ (CBR) n

=(4.104 ± 0.009) × 10

Ω

=(5.06 ± 0.4) × 10

−5

=(2.725 ± 0.002) K

, ν

=(3/11)n

0.0006 <Ω

< 0.015

(per species)

baryons n

∼ 0.25 ± 0.01 Ω

=(0.044 ± 0.004)

cold dark n

= ρ

CDM

Ω

CDM

=0.226 ± 0.04

matter (m

unknown)

“vacuum” 0 Ω

∼ 0.73 ± 0.04

total Ω

∼ 1.02 ± 0.02

9.1.1 The visible Universe

The “building blocks” of the visible Universe are galaxies which are them-

selves composed of stars, interstellar gas, and unidentiﬁed dark matter.

Galaxies have a wide variety of shapes (spirals, ellipticals and irregulars),

masses, and luminosities. Nevertheless, most of the light in the Universe is

produced in galaxies containing 10

to 10

stars that generate a typical

galactic luminosity of

L

gal

∼2 × 10



, (9.7)

where L



is the solar luminosity, L



=2.4 × 10

eV s

−1

. The mass of the

visible matter in a galaxy is typically

M

gal

∼4 × 10



, (9.8)

Galaxies are not uniformly distributed in space, a fact that is not sur-

prising in view of their mutual gravitational attraction. Galaxies are often

grouped in bound clusters, the largest of which contain thousands of galax-

ies. In spite of this “small-scale” inhomogeneity, at large scales > 100 Mpc

the Universe appears to be uniform with a number density of visible galaxies

gal

∼ 0.005 Mpc

−3

(9.9)

9.1 The Universe today 401

corresponding to a typical intergalactic distance of ∼ 6 Mpc. The total mass

density ρ

vis

associated with the “visible” parts of galaxies is

vis

= M

gal

n

gal

∼ 3 × 10



Mpc

−3

. (9.10)

The density of visible matter (9.10) divided by ρ

gives

Ω

vis

≡

vis

∼ 0.002 (9.11)

9.1.2 Baryons

The total density of ordinary “baryonic matter” (protons, nuclei and elec-

trons) is estimated to be an order of magnitude greater than that of visible

baryons (9.11):

Ω

=0.044 ± 0.004 . (9.12)

This estimate came originally from the theory of the nucleosynthesis of the

light elements which correctly predicts the relative abundances of the light

elements only if Ω

is near this value.

Since Ω

>Ω

vis

one can wonder where the missing “dark” baryons are.

Most of them are thought to be in the intergalactic medium in the form of

an ionized gas [98]. Some fraction of them may be in dark compact objects

such as dead stars (neutron stars or white dwarfs) or stars too light to burn

hydrogen (brown dwarfs). It has also been suggested [99] that a signiﬁcant

fraction of the baryons are contained in cold molecular clouds.

Finally, we mention that there are apparently very few antibaryons in the

visible Universe [100]. Any antimatter consisting of antibaryons and positrons

would quickly annihilate in collisions with ordinary matter. Even if the anti-

matter were somehow separated from the matter, annihilations in intergalac-

tic space at the boundaries between matter and antimatter domains would

lead to a ﬂux of high-energy annihilation photons. It thus seems probable

that the density of antimatter is extremely small within the accessible part

of the Universe.

9.1.3 Cold dark matter

About 90% of the matter in galaxies and clusters of galaxies is not visible.

Structure formation theories suggest that the invisible “dark matter” is “cold

dark matter,” i.e. non-relativistic matter that has only weak interactions

with baryonic matter and photons. Often, it is assumed to be in the form of

nonbaryonic weakly interacting massive particles called generically “wimps.”

The present density of CDM is estimated to be an order of magnitude greater

than that of baryons but still less than critical

Ω

CDM

=0.226 ± 0.04 . (9.13)

402 9. Nuclear Cosmology

This dark matter is believed to make up most of the mass of galactic halos

and galaxy clusters.

Unfortunately, there are no wimps in the zoo of known elementary parti-

cles and their existence is a bold prediction of cosmology. Some extensions of

the standard model of particle physics predict the existence of wimps that are

suﬃciently heavy that they would not yet have been produced at accelerators.

For example, a class of models that predict the existence of wimps are “su-

persymmetric” models. In these models, each of the known fermions (bosons)

is paired with a heavy supersymmetric partner that is a boson (fermion). The

lightest of the supersymmetric partners (LSP) is expected to be stable and

to have only weak interactions, making it an ideal wimp candidate. In Sect.

9.8 we will see that the parameters of the supersymmetric model can be cho-

sen so that the wimp has the required present-day density (9.13). The mass

would be expected to be between 10 GeV and 10 TeV. Eﬀorts are underway

to produce supersymmetric particles at accelerators and to detect them in

the Milky Way (Exercises 9.7).

9.1.4 Photons

The most abundant particles in the Universe are the photons of the “cosmic

(microwave) background radiation” (CBR) (also referred to in the litera-

ture as “CMB” for “Cosmic Microwave Background”). These photons have

a nearly perfect thermal spectrum as shown in Fig. 9.1. The photon temper-

ature is

=2.725 K ⇒ kT =2.35 × 10

−4

eV (9.14)

corresponding to a number density of

= 410.4cm

−3

. (9.15)

This is considerably greater than the number of photons that have been

generated by stars (Exercise 9.1). Despite their great abundance, the low

temperature of the CBR results in a small photon energy density, ρ

∼ n

kT:

Ω

=(5.06 ± 0.4) × 10

−5

. (9.16)

The present-day Universe is nearly transparent to photons (Exercise 9.2)

in the sense that the photon mean free path is greater than the distance to

the most distant visible objects. The CBR photons were thermalized in the

early Universe when the temperature was > 0.26 eV and baryonic matter was

completely ionized. At T ∼ 0.26 eV, baryonic matter “recombined” to form

atoms and the resulting decrease in the photon–matter cross-section made

the Universe transparent.

The CBR temperature is not completely isotropic but is observed to vary

by factors of order 10

−5

according to the direction of observation. These small

variations are believed to be due to the density inhomogeneities present at

the moment of recombination. As such, the temperature anisotropies provide