Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

8.2 Nuclear burning stages in stars 363

8.2 Nuclear burning stages in stars

In this section we will give some of the details of the various stages of stellar

nuclear burning. These stages are summarized in Table 8.1.

Table 8.1. The energy released in the (idealized) stages that transform 56 protons

and 56 electrons to one

Fe nucleus and 26 electrons. Columns 2 and 3 give the

available energy. We see that most of the energy comes in the ﬁrst stage when

hydrogen is fused to helium. The fourth column gives f

, the fraction of the energy

released that goes to neutrinos and is therefore not available for heating the medium.

(For hydrogen burning, this fraction depends on the precise reaction chain that

dominates and we have taken those in the Sun.) The ﬁnal two columns give the

approximate stellar ignition temperatures. It should be emphasize that the ﬁve

stages listed here do not represent distinct stages in real stars, in which many

diﬀerent reactions may take place simultaneously but at diﬀerent depths.

reaction Q/56 Q/m f

TkT

(MeV) 10

Jkg

−1

(10

K) (keV)

14[4

H →

He] 6.683 640 0.02 0.015 1.3

2[7

He →

O] 0.775 75 0 0.15 15

O →

Si] 0.598 57 0 0.8-2.0 100

Si →

Ni 0.195 19 0 3.5 300

Ni →

Co →

Fe 0.120 12 0.2

total 8.371 803 .02

8.2.1 Hydrogen burning

There are four principal ways of converting 4

Hto

He via exothermic re-

actions.

The ﬁrst, called “PPI ” uses only

H as the primary ingredient.

The second two, “PPII” and “PPIII” use

He as a catalyst. The fourth, the

“CNO” cycle, is catalyzed by

C and, as such, is only possible in second

generation stars. (The ﬁrst stars created in the Universe contained essen-

tially only the

Hand

He produced in the primordial Universe.) Since two

protons must be converted to neutrons, each chain has two reactions due to

weak interactions, producing two ν

Only exothermic reactions are allowed because of the relatively low temperatures

of hydrogen-burning stars.

364 8. Nuclear Astrophysics

The PPI chain proceeds as follows:

H →

(8.38)

H →

He γ

H →

He γ . (8.39)

He →

He 2

H . (8.40)

Because of the non-existence of

He and

n, reaction (8.38) is the only

reaction involving only

H. PPI thus starts with two such reactions, trans-

forming two protons to neutrons.

Once deuterium is formed by (8.38), it is in principle possible to directly

produce

He via the reaction

H →

Heγ. Since there is little deuterium

initially present in the star, a much more likely possibility is that the

produced by (8.38) quickly captures one of the abundant protons in reaction

(8.39) to produce

He.

There are no non-weak exothermic reactions between

Hand

He so,

unless one uses

He as a catalyst, the star has to wait until the quantity of

He builds to the point where

He can be produced by reaction (8.40). This

reaction terminates PPI. After annihilation of the positrons from (8.38) with

electrons in the medium, the complete chain is

−

H[2

H] → 2e

− 4

He 2ν

H] . (8.41)

where the two

H in brackets are catalysts returned in the ﬁnal reaction

(8.40). In this expression, we ignore the photons which, along with the kinetic

energy of the charged particles, are thermalized.

To avoid waiting for the buildup of

He, a star can make use of the

abundant

He as a catalyst. This is done in the PPII and PPIII chains as

follows:

H →

(8.42)

H →

He γ (8.43)

He →

Be γ (8.44)

− 7

Be →

Li ν

(PPII) or

Be →

B γ (PPIII) (8.45)

Li →

Be γ

B →

Be e

(8.46)

Be → 2

He . (8.47)

In these two cycles, the

He capture (8.40) in PPI is replaced by

He capture

producing

Be (8.44). PPII and PPIII then diﬀer through the fate of the

Be.

In the PPII chain, the

Be captures an electron to produce

Li which then

captures a proton to produce the α-unstable

Be. In the PPIII chain, the

Be captures a proton to produce

Bwhichthenβ-decays to

Be. In both

cases, the ﬁnal decay

Be →

He returns the catalyzing

He introduced

in (8.44).

The complete PPII and PPIII chains are the same as PPI (8.41) except

that the catalyst is

He instead of 2

The ﬁnal “CNO” chain uses

Cor

N as a catalyst.

8.2 Nuclear burning stages in stars 365

C →

N γ (8.48)

N →

(8.49)

C →

N γ (8.50)

N →

O γ (8.51)

O →

(8.52)

N →

He or

N →

O γ (8.53)

O →

F γ (8.54)

F →

(8.55)

O →

He (8.56)

The cycle branches at (8.53) when the proton capture can lead to the produc-

tion of

C or, through radiative capture, of

O. The catalyzing

Cor

introduced at (8.48) or (8.51) is returned at the terminating reaction (8.53)

or (8.56).

The CNO chain avoids the use of the weak two-body reaction (8.38), the

protons being transformed to neutrons via the β-decays of

Nand

Oorof

Oand

F. Since it uses heavy nuclei as catalysts, this reaction chain was

not possible for the ﬁrst generation of stars.

The relative importance of the four hydrogen burning chains depends

on the mass and chemical composition of the star. First generation stars

with practically no carbon cannot use the CNO cycle. For stars with Solar-

type compositions, the CNO chain avoids the initial weak interaction (8.39)

but it is still estimated to be unimportant in the Sun because of the high

Coulomb barrier for proton capture on carbon. The CNO cycle is important

in high-mass hydrogen-burning stars because the burning temperature is an

increasing function of the mass. This is because the luminosity is proportional

to the third power of the mass and the high reaction rate needed to provide

the large luminosity requires a high burning temperature.

In stars burning with the PP chains, the (PPII+PPIII) to PPI ratio is

determined by the relative probability for a

He to capture another

or a

He. Capture of a

He has a higher probability for Coulomb barrier

penetration because of the higher thermal velocity of

He compared to

He.

Low-mass stars therefore prefer PPI. This is the case in the Sun, where 90%

of the energy is produced by PPI. In low-mass stars, PPII is favored by over

PPIII because of the lack of a Coulomb barrier for (8.45). In the Sun, 10%

of the luminosity is generated by PPII and 0.02% by PPIII. About 1% is

generated by the CNO cycle.

366 8. Nuclear Astrophysics

8.2.2 Helium burning

After the core of a main sequence star is transformed to

He, it contracts

until the temperature is suﬃciently high that the star’s luminosity can be

provided by helium burning. The mechanism of

He burning is quite diﬀer-

ent from that of hydrogen burning. There is no lack of neutrons so weak

interactions are not needed. On the other hand, helium burning is strongly

inhibited by the fact that there are no exothermic two-body reactions in-

volving only

He. In particular, the mass of

Be is 92 keV greater than twice

the mass of

He and therefore decays immediately (τ =2× 10

−16

s) back to

He:

He ↔

Be |Q| = 92 keV (8.57)

Unlike the irreversible production of

He from

H due to strongly exother-

mic reactions, the production of

Be is thus endothermic and reversible. As

we showed in Sect. 4.1.5, a thermal equilibrium abundance of

Be is built up

given by:

8Be

4He

(mkT )

3/2

/(4π

¯h

)

−92 keV/kT

, (8.58)

where m is the

He−

He reduced mass. The typical density in a

He-burning

core are ρ ∼ 10

gcm

−3

and kT ∼ 15 keV, so (8.58) gives only a tiny

abundance of ∼ 10

−9

of the

He abundance.

Using this small abundances of

Be, it is possible to produce

C through

the reaction

Be →

C γ Q=7.366 MeV (8.59)

Because of the very small quantity of

Be, this would normally lead to a

very small production rate of

C. However, as we noted in Sect. 7.1.3, the

rate can be greatly increased if

C has an excited state near the Gamow

energy for the reaction, E

∼ 200 keV for kT ∼ 15 keV. This lead Hoyle [75]

to predict the existence of such a state and subsequent measurements lead

to its discovery (Fig. 8.5). This 0

excited state of

C is 7654 keV above

the

C ground state and 283 keV above

He −

Be. It decays mostly via α

decay, returning the original

Be, but also has a ∼ 10

−3

branching ratio to

thegroundstateof

Be →

∗

Q=−283 keV

∗

→

He Γ =8.3eV

∗

→

C γγ Γ

=3× 10

−3

eV (8.60)

The irreversible production of

C thus proceeds through

He →

Be →

∗

→

C γγ . (8.61)

This sequence is called the “triple-α” process.

Only the core must contract so that the gravitational radius decreases. The

envelope of the star expands so that the stars appears as a red giant.

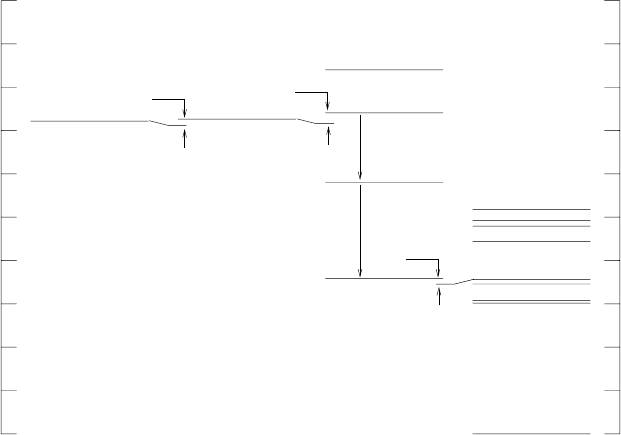
8.2 Nuclear burning stages in stars 367

3−

1−

92keV

283keV

45keV

E (MeV)

Fig. 8.5. The energy levels of four

He nuclei.

The energy liberated by the triple-α process can generate the star’s lumi-

nosity when the central temperature reaches kT ∼ 10 keV, i.e. T ∼ 10

K. As

the

Heinthecoreisdepleted,

C burning is initiated via the non-resonant

reaction

C →

O γ Q=7.162 MeV (8.62)

This reaction competes favorably with the triple-α process once the

He is

depleted because its rate is linear in the concentration of

He while the rate

of the triple-α process is proportional to the third power of the

He con-

centration. The helium-burning stage thus generates a mixture of

Cand

A peculiar characteristic of the triple-α process is that its end result de-

pends critically on the details of the three remarkable energy alignments of

the 0

states of

Be,

Candthe1

−

state of

O (Fig. 8.5):

He →

Be Q

= −0.092 MeV , (8.63)

Be →

∗

= −0.283 MeV , (8.64)

C →

∗

γ Q

=+0.045 MeV . (8.65)

The alignment results in the three reactions being respectively slightly en-

dothermic, slightly endothermic, and slightly exothermic. It turns out that

368 8. Nuclear Astrophysics

this is the only possible arrangement that leads to signiﬁcant production of

First, making reactions (8.63) or (8.64) more endothermic by increasing

their Q-values would have the eﬀect of increasing the temperature at which

the triple-α process takes place. At this higher temperature the Coulomb

barrier for the

He −

C reaction would be less eﬀective so the carbon pro-

duced by the triple-α process would be quickly burned to

O, leaving little

carbon. According to [76], an increase of 250 keV in the

∗

resonance leads

to negligible production of

Changing the signs of the Q-values (while keeping them small) leads to

more interesting scenarios. If (8.63) were exothermic, the hydrogen burn-

ing phase would be followed be a helium burning phase producing only

through

He →

Beγ.Thisphasewouldthenbefollowedatahigher

temperature with a beryllium burning phase with the production of oxygen

via 2

Be →

Oγ.

C would be largely bypassed in this scenario.

On the other hand, if reaction (8.64) were exothermic, the triple-α pro-

cess would not be possible at all since the production of

∗

would not be

resonant.

Finally, if reaction (8.65) were slightly endothermic rather than slightly

exothermic,

He absorption by

C would be resonant so the

Cwouldbe

quickly burned to

O. Once again, little

C would be produced.

Carbon is unique among low-mass elements as having a chemistry that is

suﬃciently rich to allow for life “as we know it” on Earth. Its production in

stars depends upon a delicate alignment of nuclear levels. This alignment is,

in turn, sensitive to the values of the fundamental parameters of physics like

the electroweak and strong interaction couplings. In particular, the aforemen-

tioned increase by ∼ 200 keV in the 0

level of

C would require a change

in the nucleon–nucleon potential of order 0.5% or in the ﬁne-structure con-

stant of order 4% [77]. Such estimates should, however, be treated with cau-

tion since many correlated changes in physics might occur if the parameters

changed.

This sensitivity of stellar nucleosynthesis to nuclear levels is similar to the

sensitivity of cosmological nucleosynthesis to the neutron–proton mass diﬀer-

ence and the binding energies of the A = 2 nuclei. In that case, the physical

parameters are such that they prevent hydrogen from being eliminated in the

primordial Universe, thus leaving us with a store of available free energy.

As emphasized in the introduction, these facts have inspired speculations

concerning the possibility that the physical constants are dynamical variables

that can take on diﬀerent values in diﬀerent parts of the Universe. We know

that physics seems to be the same in other parts of the visible Universe, so

these variations must take place on scales larger than our “horizon,” i.e. the

distance to the furthest visible objects. At any rate, in such a picture, there

will be some parts of the Universe where the parameters take on values that

allow for the production of large quantities of carbon. To the extent that a

8.2 Nuclear burning stages in stars 369

large quantity of carbon increases the probability for the emergence of life, it

would then be natural that we ﬁnd ourselves in such a region.

8.2.3 Advanced nuclear-burning stages

The later stages of nuclear burning are rather complicated for reasons of both

astrophysics and nuclear physics.

The nuclear reaction chains are rather complicated because of the multiple

ﬁnal states for reactions involving two nuclei. For example, in carbon burning,

there are three possible exothermic reactions:

C →

Mn γ Q=13.93 MeV

→

Nap Q=2.24 MeV

→

He Q=4.62 MeV .

These three reactions can be considered to be a single reaction consisting of

the formation of a “compound nucleus,” i.e. an excited state of

Mn which

then decays by photon, proton, or α emission

C →

∗

→ xy. (8.66)

Proton or α emission have larger probabilities than photon emission. The

protons and α-particles produced in

∗

decay is are then absorbed by

C to produce

Nor

After carbon, neon and oxygen burning, the temperature becomes suﬃ-

ciently high that some heavy nuclei are photo-dissociated by the ejection of

α’s. The abundance of

He becomes suﬃciently high that α-capture becomes

the major reaction leading up to the production of iron-peak nuclei.

The astrophysics of the later stages is complicated by several facts. First,

in massive stars, an advanced nuclear stage in the hot core of a star may

alternate with “shell burning” in the outer regions of an earlier (hydrogen

or helium) stage. Second, a core will be hot enough to initiate the thermal

production of neutrinos. Because of their long mean-free paths, neutrino ra-

diation is the dominant source of stellar energy loss and the total (neutrino

plus photon) luminosity given by (8.26) increases. This results in a shorten-

ing of the duration of these neutrino-radiating stages. Finally, a particular

core burning stage may be reached when the electrons are degenerate. As

already emphasized, under such circumstances, the nuclear thermostat is not

operativeandtheburningmaybeexplosive.

The best examples of explosive burning are type Ia supernovae. The pro-

genitor of these supernovae are believed to be carbon–oxygen white dwarfs

supported by degenerate electrons. Such an object would be an star with

a core that has completed it helium-burning and that has lost to a large

extent its helium–hydrogen envelope through various processes. An isolated

white dwarf will simply cool down but if it has a binary companion, it can

370 8. Nuclear Astrophysics

accrete matter until it reaches the Chandrasekhar mass (8.33). At this point,

the star becomes unstable and will explosively burn its carbon and oxygen to

Ni. The energy liberated is enough to completely disrupt the gravitationally

bound star (Exercise 8.3).

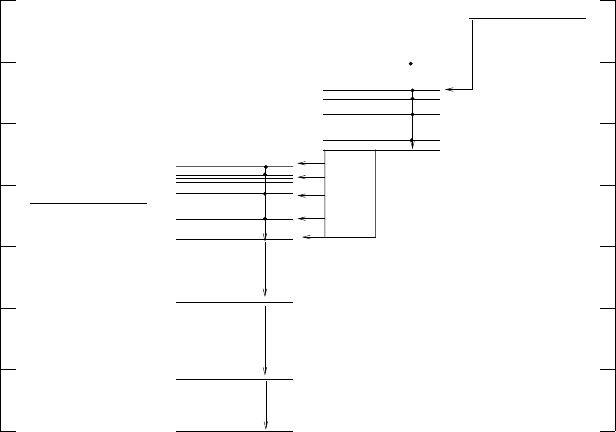
After disruption of the star, the supernova continues to produce energy

via the β-decays of

Ni and

Co (Fig. 8.6). The lifetimes of these two nuclei

determine the luminosity as a function of time of the supernova starting about

a week after explosion. An example of this is shown in Fig. 0.1 for Kepler’s

supernova.

81%

β+ 19%

846.7 keV

1238.3 keV

E (MeV)

Fig. 8.6. The A = 56 system showing the ﬁnal stage of stellar burning, the β-decays

Ni and

Co.

8.2.4 Core-collapse

Stars with M>20M



will burn their cores to

Fe.Atthispoint,thestar

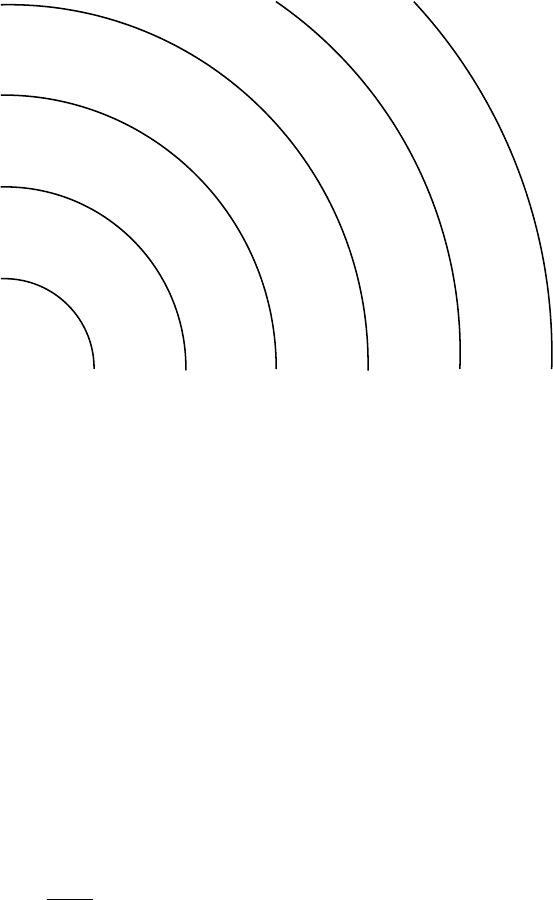
proﬁle will look something like the pre-supernova conﬁguration shown in Fig.

8.7. The various core- and shell-burning phases may have left an onion like

structure with heavy elements at the center and the original hydrogen–helium

mix at the surface. Depending on mass-loss during the lifetime of the star,

some of the outer layers may be missing

When the star reaches this conﬁguration there is nothing left to burn

in the core. The inert core will then accumulate mass until it reaches the

8.2 Nuclear burning stages in stars 371

Si−S

M(r)=2

M(r)=5

M(r)=2.6

M(r)=6

ρ=10

O−Mg

C−Ne

H−He

ρ=10

M(r)=8 M=25

ρ=10

Fig. 8.7. The proﬁle of a 25M



star when its core has burned to

Fe. For each con-

centric shell, the characteristic density (in gm cm

−3

) and dominant nuclear species

are shown.

Chandrasekhar mass. At this point, it will start to implode since no ther-

mal pressure can balance gravitation. As the temperature rises, the nuclei

will start to evaporate to

He and then to nucleons. At the same time, the

Fermi level of the electrons becomes suﬃciently high that the electron are

suﬃciently energetic to be captured on protons to form neutrons

−

p → nν

. (8.67)

The ν

will escape from the star (Exercise 8.4). That these three distinct

events, collapse, nuclear evaporation, and neutronization, all occur at roughly

the same moment is due to the “coincidence” that the electron mass, nuclear

binding energies, and the proton–neutron mass diﬀerence are all in the MeV

range.

Once the protons have been converted to neutrons, the collapse may be

halted at the radius corresponding to a degenerate gas of neutrons. The

energy change of the 1.4M



core in the process of collapsing from R ∼

1000 km to R ∼ 10 km is

∆E ∼ (3/5)

∼ 3 × 10

JforM =1.5M



. (8.68)

Because of their long mean-free paths, the energy is almost entirely evac-

uated in the form of thermally produced neutrinos and antineutrinos. The

produced in the supernova SN1987a in the neighboring galaxy the Large

Magellanic Cloud were detected (Exercise 3.2) conﬁrming the core-collapse

372 8. Nuclear Astrophysics

mechanism for type II supernova. These observations are described in Sect.

8.4.2.

The outer layers of the of the supernova are blown oﬀ into the interstellar

medium. These layers are rich in intermediate mass nuclei A = 4 to 56 and

are a major source of the nuclei present on Earth. It is also believed that the

proto-neutron star generates a large neutron ﬂux that creates many heavy

nuclei through neutron capture, as discussed in Sect. 8.3.3.

Many of the nuclei ejected from the supernova are radioactive. Were it not

for this source of energy, the matter would quickly cool and become invisible.

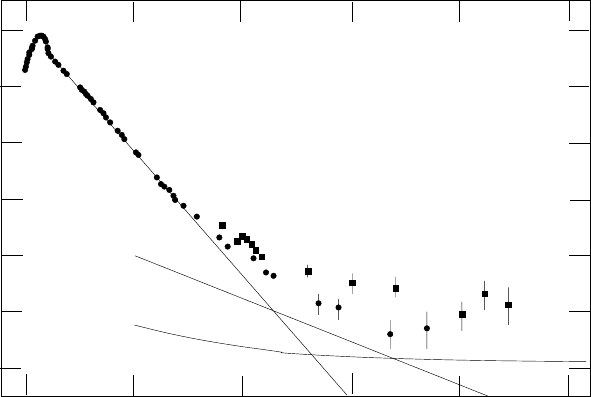
Figure 8.8 shows how the observed luminosity of SN1987a declined with the

lifetime of

Co indicating that this decay (Fig. 8.6) is the primary energy

source for the expanding cloud. A conﬁrming observation (Sect. 8.4.3) is that

the γ-rays from

Co decay were observed in the direction of SN1987a. After

several

Co lifetimes, it is believed that the supernova remnant is powered

by other, longer-lived, radioactive nuclei.

500

1000

1500

2000

t (days)

L (joule/sec)

Fig. 8.8. The total luminosity of SN1987a as a function of time [78]. The labeled

curves show the calculated contribution to the luminosity from the β-decay of

Co,

Co, and

Ti.