Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology
Подождите немного. Документ загружается.

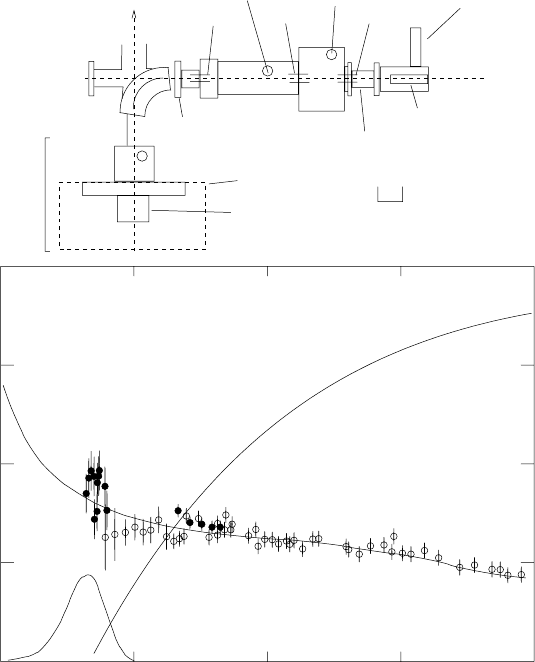
7.1 Fusion reactions 333
10
−12
10
10
−9
−6
−3
0
10
10
cross−section (b)
0
8
12
16
4
S(E) (MeV b)
10
100
1000
E (keV)
ion source
Faraday cage
90 deg double−
focusing magnet
1st pump gas inlet
beam calorimeter
target chamber
2nd pump
50 kV accelerator
electromagnetic
to 3rd pump
steerer
aperature
aperature
aperature
10 cm
Fig. 7.1. Cross-section and S(E) for
3
He
3
He →
4
He p p, as measured by the
LUNA underground accelerator facility [69]. The top panel shows the small (∼ 1m
2
)
experiment consisting of a
3
He ion source, a 50 kV electrostatic accelerator, an
analyzing magnetic spectrometer, a gaseous (
3
He) target chamber, and a beam
calorimeter to measure the beam intensity. The sides of the target chamber are
instrumented with silicon ionization counters that measure dE/dx and E of protons
produced by
3
He +
3
He →
4
He + p p in the chamber. Because of the very small
cross-sections to be measured, the experiment is in the deep underground laboratory
LNGS, Gran Sasso, Italy, where cosmic-ray background is eliminated. The bottom
panel shows the LUNA measurements as well as higher energy measurements [70].
The lowest energy measurements cover the region of the solar Gamow peak for this
reaction (Fig. 7.3). Note that while the cross-section varies by more than 10 orders
of magnitude between E = 20 keV and 1 MeV, the factor S(E) varies only by a
factor ∼ 2.
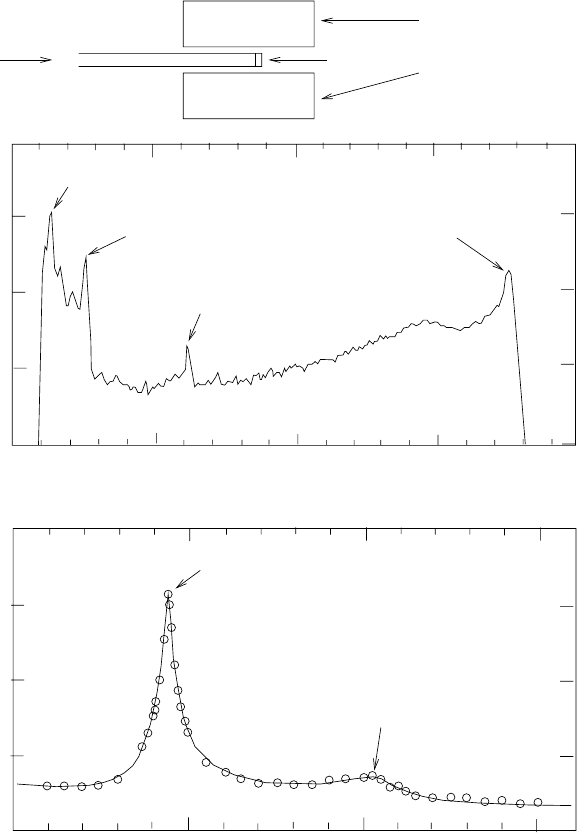
334 7. Fusion
1
−1
1
2
10
10
10
10
3
S(E) (keV−b)
photon energy (MeV)
500
1000
1500
proton energy (keV)
4
5
10
10
10
10
5
10
15
2
0
proton beam
target
12 x 12 inch
NaI
scintillator
3
2
1
10
counts
40
K
208
Tl
F(p, αγ) O
16
19
Li(p,
γ)
8
Be
7
E=1080 keV
E=441 keV
Fig. 7.2. S(E) for p
7
Li →
8
Be γ as measured by [71]. The top panel shows how a
proton beam impinges upon a target consisting of 10 µgcm
−2
of LiF evaporated on
a copper backing. The target is inside a large NaI scintillator that detects photons
emerging from the target. The middle panel shows a typical photon energy spectrum
showing peaks due to
7
Li(p, γ)
8
Be, in addition to peaks due to
19
F(p, αγ)
16
O and
to natural radioactivity in the laboratory walls. The S-factor deduced from the
photon counting rate is shown on the bottom panel as a function of proton energy.
It shows the presence of two resonances due to excited states of
8
Be.

7.1 Fusion reactions 335
σ(E)=
S(E)
E
exp
−
E
B
/E
. (7.15)
where S(E) is a slowly varying function of the center-of-mass energy and E
B
is given by (7.14).
The experimental determination of the nuclear factors S(E) is a problem
of major interest for all calculations in astrophysical and cosmological nucle-
osynthesis, as we shall see in the next chapters. Examples are shown in Figs.
7.1 and 7.2. Considerable effort has been made in recent years to measure the
cross-sections at energies comparable to stellar temperatures. Without such
data it was necessary to extrapolate the S(E).
Table 7.1 lists the S(E) for some important fusion reactions. Note that the
tiny cross-section for the stellar reaction pp →
2
He
+
ν
e
makes this reaction
unobservable. The S(E) must therefore be calculated using weak-interaction
theory.
The Gamow formula (7.15) can also be obtained quite easily in the Born
approximation. A cross-section involves, like any transition rate, the square
of a matrix element between initial and final states |f|M|i|
2
. When forces
are short range, the asymptotic states |i and |f are monochromatic plane
waves.
In the presence of a Coulomb interaction, which is of infinite range, the
asymptotic behavior is different. The wave function is exactly calculable (see
for instance A. Messiah, Quantum Mechanics vol. 1, chap. XI-7) and, asymp-
totically, the argument of the exponential has additional terms of the form
ϕ(r) ∼ exp(i(kr + γ log kr)) with γ = Z
1
Z
2
e
2
/4π
0
¯hv . (7.16)
These asymptotic wave functions are called Coulomb scattering states. Con-
sider, for instance, the reaction d + t →
4
He + n. In the initial state, we must
use Coulomb scattering states (and not the usual asymptotic states). Since
the strong interaction is short range, we can, in good approximation, simply
multiply the usual matrix element by the value of the Coulomb scattering
wave at the origin ψ
coul
(0) = Γ (1 + iγ)e
−πγ/2
, i.e. multiply the nuclear cross
section by the factor |Γ (1 + iγ)e
−πγ/2
|
2
= πγe
−πγ
/ sinh πγ. Once the kine-
matic factors are taken into account, one recovers the tunnel effect factor
e
−2πγ
∼ e
−πγ
/ sinh πγ introduced empirically for γ = Z
1
Z
2
e
2
/4π
0
¯hv 1.
7.1.2 Reaction rate in a medium
Consider the specific case of a mixture of deuterium and tritium. We want to
evaluate the reaction rate per unit volume, i.e. the number R of reactions per
unit volume and unit time, if the number densities of d and t are respectively
n
1
and n
2
. Knowing this rate, we can readily calculate the power emitted.
Consider a deuterium nucleus, of velocity v with respect to the tritium
nucleus. As discussed in Sect. 3.1.4, the probability per unit time λ that a
fusion reaction occurs is:
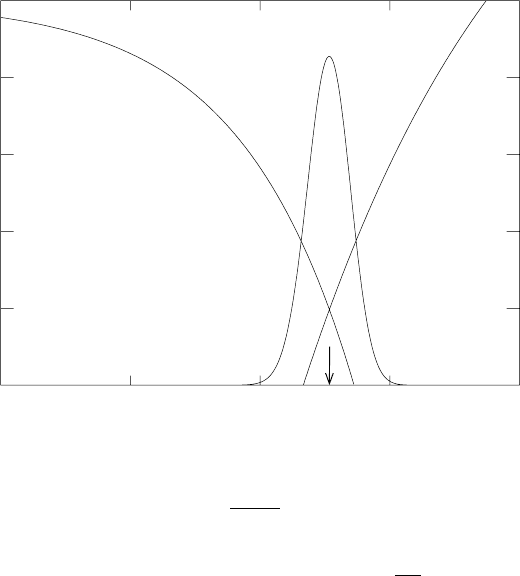
336 7. Fusion
110
1
−2
10
−4
10
−6
10
−8
10
−10
10
exp(−E/kT)
10
10
10
10
10
−16
−14
−12
−10
−8
P(E)
10
−18
100
(keV)
c
m
E
E
G
=18.5 keV
Fig. 7.3. Factors entering the calculation of the pair reaction rate (7.22). The
Boltzmann factor exp(−E/kT) (logarithmic scale on the left) and the barrier pen-
etration probability P (E)=exp(−
E
B
/E) (7.13) (logarithmic scale on the right)
are calculated for kT = 1 keV (corresponding to the center of the Sun) and for the
reaction
3
He
3
He →
4
He pp. The product is the Gaussian-like curve in the center
(shown on a linear scale). It is maximized at E
G
=(
√
E
B
kT/2)
2/3
∼ 18.5 keV
and most reactions occur within ∼ 5 keV of this value. Note the small values of
exp(−E
Gm
/kT ) ∼ 10
−8
and P (E
G
) ∼ 10
−16
.
λ = n
2
σ(v) v (7.17)
where σ is the fusion cross-section (7.15). The rate per unit volume is then
found by multiplying the rate per deuterium nucleus by n
1
:
R = n
1
n
2
σ(v)v. (7.18)
We must average this expression over the velocity distribution in the medium
at temperature T :
R = n
1
n
2
σ(v)v (7.19)
where σ(v)v is the average of the product σ(v)v, the probability of v being
determined by the Maxwell distribution at temperature T . Because of the
decreasing Coulomb barrier, the product σv increases rapidly with the en-
ergy. In the averaging, it is however in competition with the decrease of the
Maxwell distribution with increasing velocity. If only one of the two species
is in motion, we would have

7.1 Fusion reactions 337
σv∼
d
3
v e
−E/kT
σ(v)v ∼
v
3
e
−mv
2
/2kT
σ(v)dv. (7.20)
In reality, both species are in motion so the integral is slightly more compli-
cated. For nuclear of masses of m
1
and m
2
,wehave
σv =
m
1
2πkT
3/2
m
2
2πkT
3/2
e
−(m
1
v
2
1
+m
2
v
2
2
)/2kT
σ(v)v d
3
v
1
d
3
v
2
,
where v = |v
1
− v
2
| is the relative velocity. Turning to center-of-mass vari-
ables, µ = m
1
m
2
/(m
1
+ m
2
) being the reduced mass, we can integrate over
the total momentum (or the velocity of the center of gravity). This leads to
σv =
8
πµ(kT)
3
e
−E/kT
Eσ(E)dE. (7.21)
Using (7.15) this is
σv =
8
πµ(kT)
3
e
−
√
E
B
/E
e
−E/kT
S(E)dE. (7.22)
The integrand contains the product of two exponentials shown in Fig. 7.3.
Their product peaks at the Gamow energy
E
G
= E
1/3
B
(kT/2)
2/3
, (7.23)
where E
B
is given by (7.14). As long as S(E) has no resonances (e.g. as
in Fig. 7.2) only the narrow region around the Gamow energy (called the
Gamow peak) contributes significantly to σ(v)v. Its position determines
the effective energy at which the reaction takes place.
In the absence of resonances, the nuclear factor S(E) varies slowly and
only the value S(E
G
) is relevant so it can be taken out of the integral (7.22).
We can also make a Taylor expansion of the argument of the exponential in
the region E
G
:
E
B
/E + E/kT ∼
3
2
E
B
kT/2
1/3
+
1
2
(E − E
G
)
2
∆
2
E
, (7.24)
where the width of the Gamow peak is
∆
E
=
2
√
3
E
G
kT
E
G
1/2
=
2
√
3
E
1/6
B
kT
2
5/6
. (7.25)
[Note that the Gamow peak is relatively narrow: ∆
E
/E
G
∼ (kT/E
B
)
1/6
.] We
then have
σv =
8π
√
µ
(kT)
−3/2
S(E
G
)exp
−(3/2)
E
B
kT/2
1/3
×
exp
(E − E
G
)
2
2∆
2
E
dE. (7.26)
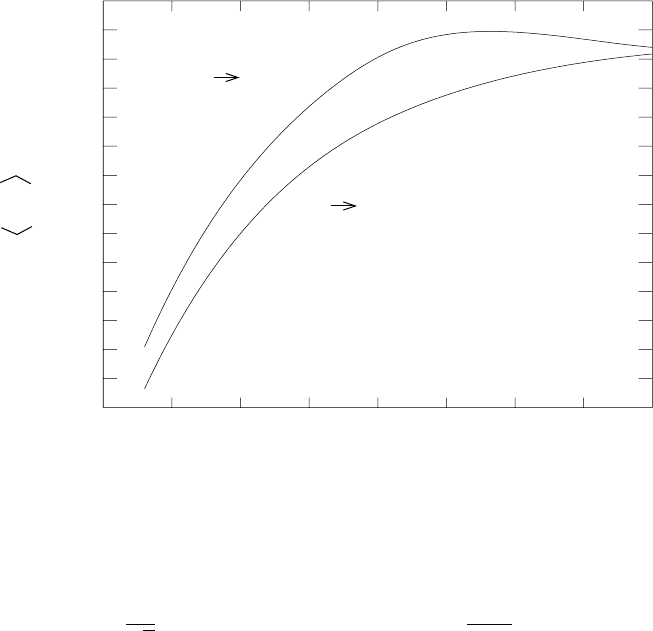
338 7. Fusion
−1 3
12
−20
−22
−24
−28
−26
−30
−32
−34
10
10
10
10
10
10
10
10
10 10 10
3
1
kT (keV)
v
σ
(m
3
s
d d He n
4
He n
3
t d
−1
)
Fig. 7.4. Variation of the pair reaction rate vσ as a function of the temperature
for d-d and d-t mixtures.
The Gaussian integral just gives a factor ∆
E
so we end up with
σv =
8π
√
µ
(kT)
−2/3
E
1/6
B
S(E
G
)exp
−(3/2)
E
B
kT/2
1/3
(7.27)
Figure 7.4 shows σv as a function of temperature for d d → n
3
He
and for d t → n
4
He. The rate rises rapidly for kT < 10 keV before leveling
off. We can say that kT ∼ 10 keV , i.e. T ∼ 1.5 × 10
8
K, defines an optimal
temperature for a fusion reactor.
7.1.3 Resonant reaction rates
If a reaction cross-section exhibits resonances, like those in Fig. 7.2, then the
integral in (7.21) may also receive an important contribution from energies
near the resonance, in addition to the Gamow peak. Such resonances are due
to states of the compound nucleus consisting of the two interacting particles.
For example, the resonance in Fig. 7.2 is due to an excited state of
8
Be
(Exercise 7.3). This state can decay to both the initial particles
8
Be
∗
→ p
7
Li Γ
p
=6keV, (7.28)
and to the ground state of
8
Be

7.2 Reactor performance criteria 339
8
Be
∗
→ γ
8
Be Γ
γ
=12eV. (7.29)
Near the peak of the resonance, the cross-section for p
7
Li →
8
Be γ is given
by (3.183)
σ
i→f
(E) ∼ 4π
(¯hc)
2
2µE
(Γ
p
/2)(Γ
γ
/2)
(E − E
0
)
2
+ Γ
2
/4
, (7.30)
where we have neglected the spin factors and where Γ = Γ
γ
+ Γ
p
.Thecontri-
bution to the integral in (7.21) coming from the resonance region is then just
proportional to the cross-section on resonance, 4π(Γ
γ
/Γ )(¯hc)
2
/(2µE) times
the width Γ :
res
e
−E/kT
Eσ(E)dE ∼ e
−E
res
/kT
(¯hc)
2
µc
2
Γ
γ
. (7.31)
Comparing this with the non-resonant rate (7.22) we get the ratio of the
contributions of the resonance and the Gamow peak
σv
res
σv
Gamow
∼
e
−E
res
/kT
e
−E
G
/kT
1
e
−
√
E
B
/E
G
(¯hc)
2
/µc
2
S(E
G
)
Γ
γ
∆
E
. (7.32)
We have written the ratio as the product of four dimensionless factors. The
fourth favors the Gamow contribution, Γ
γ
/∆
E
∼ 10
−3
, while the third, ∼
10
3
favors the resonance. The relative importance is then determined by
the strongly temperature dependent first and second terms. We leave it to
Exercise 7.5 to show that in the Sun (kT ∼ 1 keV) the Boltzmann factor
suppresses the resonant contribution to a negligible level.
However, for resonances near or below the Gamow peak, the resonance
is generally more important. The most important example in astrophysics is
the reaction
4
He
8
Be →
12
C γ . (7.33)
which proceeds through an excited state of
12
C corresponding to a
4
He−
8
Be
center-of-mass energy of E
res
= 283 keV. This reaction is responsible for the
production of carbon and takes place in stars at kT ∼ 15 keV corresponding
to E
G
∼ 300 keV. In this case, the Boltzmann factors in (7.32) cancel. The
factor exp(−
E
B
/E
G
) ∼ 10
−11
then ensures that the resonant contribution
dominates.
7.2 Reactor performance criteria
A fusion reactor consists of three essential elements
• A confined plasma containing positively charged ions (generally
2
Hand
3
H) and electrons to maintain the neutrality.
• An energy injector to create and, if necessary, maintain a high temperature.
340 7. Fusion
• An energy recovery mechanism that collects the energy of escaping fusion-
produced neutrons and thermal photons.
In practice, the confinement of the plasma is achieved by three different
mechanisms: gravitational confinement, inertial confinement and magnetic
confinement. Gravitational confinement is achieved naturally in stars. The
plasma is maintained indefinitely by the self-gravitation of the star. Inertial
confinement is used in laser induced fusion. It also occurs in supernovae
explosions (and in explosive devices). Magnetic confinement has been the
main method investigated for controlled fusion before laser induced inertial
confinement was declassified.
Let V be the plasma volume, R the reaction rate as defined by (7.19) and
Q the energy released in an elementary fusion reaction. The fusion-generated
power P (before any losses are taken into account) is given by
P = RV Q . (7.34)
For a given value of the temperature, in order to increase the reaction rate
R, one must increase the densities n
1
and n
2
. For a given value of n = n
1
+n
2
,
the best proportion, which maximizes the product n
1
n
2
corresponds to n
1
=
n
2
= n/2, i.e. equal amounts of reagents, at high densities. One therefore
seeks high temperatures (∼ 10
7
K,kT ∼ 1keV) and a strong compression.
Fusion reactors are judged by how much power they create compared to
how much was used in heating the plasma. Three goals, in order of decreasing
difficulty, are defined for any fusion reactor:
• Ignition. After heating, the reaction rate is sufficiently high to maintain
the temperature without further injection of energy. In reaction (7.4), the
neutron escapes so the
4
He energy must be used to compensate for cooling
by radiation of photons and neutrons.
• Breakeven. Power generated by fusion is equal to the input power that
must be continually injected to compensate for energy losses (neutrons
and photons).
• One-shot breakeven (Lawson Criterion). The energy generated by fusion is
equal to the input energy necessary to heat the plasma. A reactor satisfying
only this criterion is similar to the sub-critical fission reactors of Sect. 6.8.
The present goal is to satisfy the Lawson criterion which we now make
more precise. The time τ during which the plasma maintains its temperature
T and its cohesion, after its creation, is called the confinement time. This
time is effectively infinite in stars, in the sense that confinement lasts at least
as long as there is some nuclear fuel left.
In order to heat the plasma to the temperature T , one must furnish, per
unit volume, the energy 3nkT where n is the number density of nuclei. (We
assume one free electron per ion).
Let η be the efficiency to transform nuclear energy into electric energy in
the reactor, in other words the efficiency to recover the energy produced by

7.2 Reactor performance criteria 341
the plasma. The reactor will run in ignition conditions if the energy spent to
heat it is smaller than the electric energy it can produce:
3nkT < (n
2
/4η)vσQτ (7.35)
where we assume that there are two species (d-t mixture) of number densities
n
1
= n
2
= n/2. We must therefore have
nτ > (
1
η
)
12kT
(Qvσ)
(7.36)
where Q is the energy produced in an elementary fusion reaction. This for-
mula is called the Lawson criterion.
From Fig. 7.4 we see that σv∝T
2
for kT ∼ 10 keV:
σv(dt →
4
He n) ∼ 10
−22
m
3
s
−1
kT
10 keV
2
. (7.37)
Substituting this into (7.36) and using Q =17.5 MeV we get the Lawson
criterion for the d-t reaction
nτ
kT
10 keV
>η
−1
1.5 × 10
20
m
−3
s , (7.38)
or equivalently
nτkT > η
−1
1.5 × 10
21
m
−3
skeV , (7.39)
In gravitational confinement, τ is effectively infinite so the Lawson cri-
terion is irrelevant. In magnetic confinement, confinement times achieved so
far are ∼ 1 s, limited by excess cooling due to impurities in the plasma and
to various plasma instabilities. The density is planned to be of the order of
10
20
m
−3
in the project ITER (International Thermonuclear Experimental
Reactor) and the temperature of the order of 10 to 20 keV, which is the igni-
tion threshold. In laser induced inertial confinement, the confinement time is
much shorter τ 10
−11
s. However, the density is much higher 10
31
m
−3
.
The temperature is comparable, of the order of 10 keV.
Table 7.2. Comparison of the parameters in three fusion confinement schemes.
Type n(m
−3
) τ(s) T (keV)
ITER Tokamak 10
20
1 10to20
Inertial; laser 10
31
10
−11
10
Sun (grav) 7. 10
30
10
17
1.3
342 7. Fusion
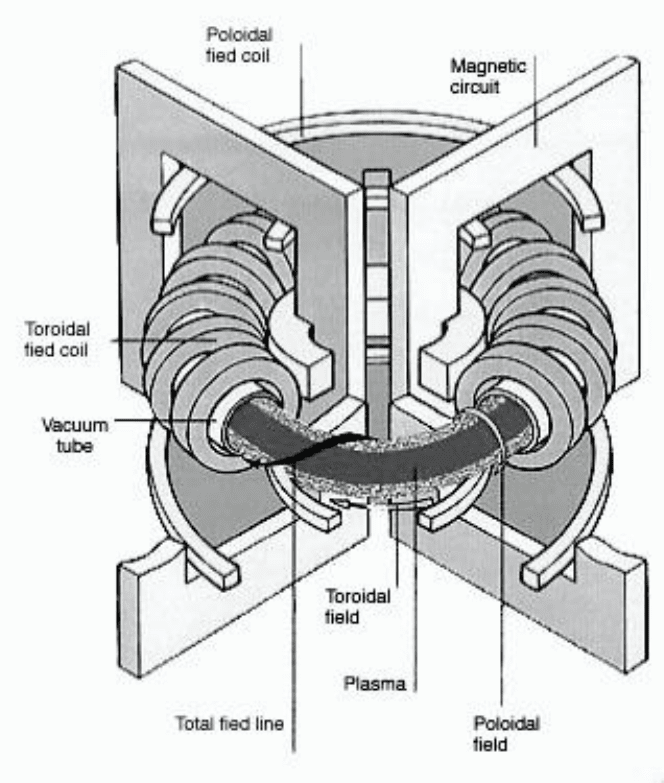
7.3 Magnetic confinement
The magnetic confinement method consists in using a magnetic field to con-
tain the plasma. Tokamaks are toroidal machines where the plasma is main-
tained inside a tube by a strong toroidal field superimposed on a poloidal
field which maintains it in the horizontal plane.
Fig. 7.5. Diagram of a Tokamak.
In the tokamak configuration shown on Fig. 7.5, the toroidal field, created
by external currents, is rotationally symmetric around the vertical axis. The
