Барковський В.В., Барковська Н.В. Вища математика для економістів

Подождите немного. Документ загружается.

381

Частина 13. Числові та степеневі ряди

Візьмемо другий додатний числовий ряд, збіжність чи розбіжність

якого

відома







b 

. (11)

Найчастіше для порівняння беруть ряд геометричної прогресії або

узагальнений

гармонічний ряд.



Ознака. Якщо ряд (11) збігається і, починаючи з деякого

nN

виконуються співвідношення

ab

, тоді й ряд (10) також збігається.

Якщо ряд (11) розбігається і, починаючи з деякого

nN

, викону&

ються співвідношення

ab

, тоді й ряд (10) розбігається.



Приклад 2. Дослідити збіжність ряду









Розв’язання. Порівняємо заданий ряд

234

11 1 1 1

222 32 42 2



 



з рядом геометричної прогресії, знаменник якого

q 

234

11 1 1 1

222 2



Кожний член заданого ряду менший або дорівнює відповідному

члену

ряду геометричної прогресії, який збігається, тому що

1q 



1, 2, 3,







Отже, заданий рад збігається.



Ознака Даламбера. Позначимо

постійну Даламбера, яку

знаходять

за формулою

lim







. (12)

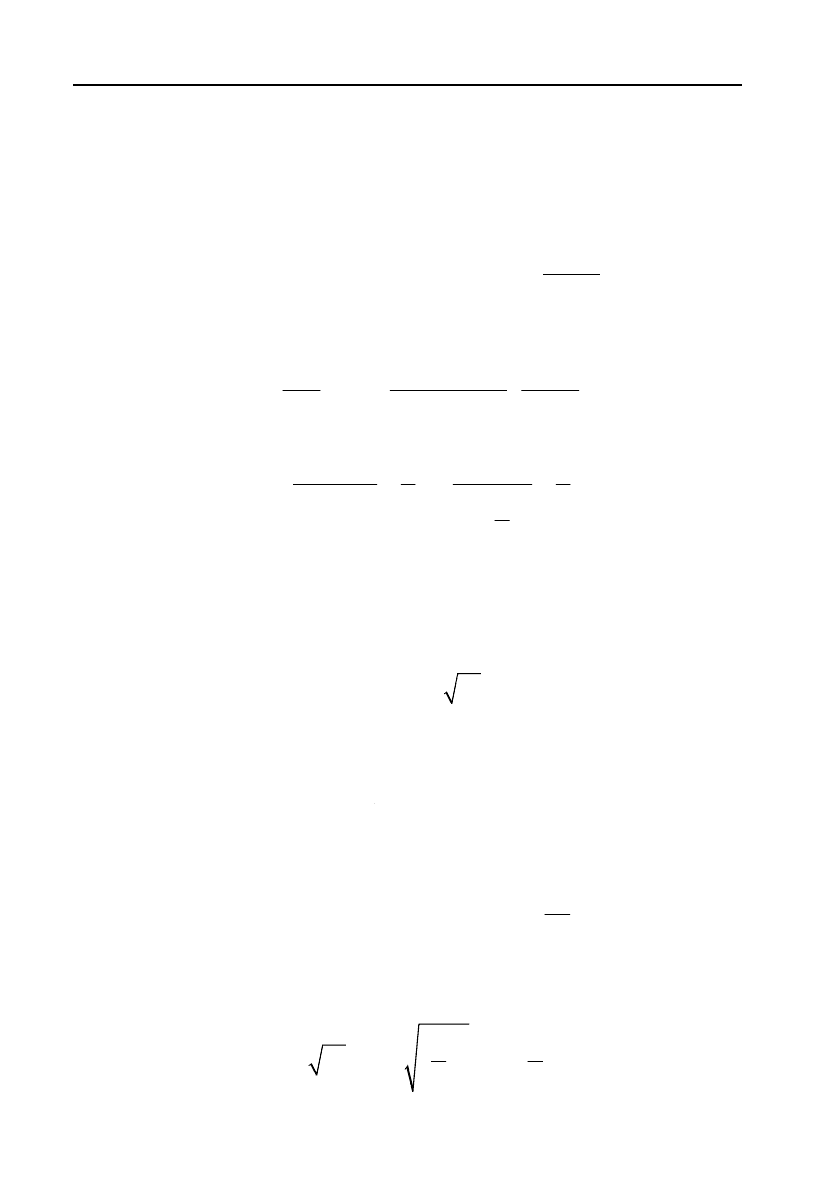
382

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

Якщо

1D 

, тоді додатний числовий ряд







збігається. При

1D 

цей ряд розбігається. При



треба застосовувати іншу

ознаку



Приклад 3. Дослідити збіжність раду











Розв’язання. Застосуємо до заданого раду ознаку Даламбера



lim lim :



 





 











3313

lim lim

21 1

 

 











Отже, заданий ряд розбігається.



Радикальна ознака Коші. Позначимо

постійну Коші, яку

знаходять

за формулою

lim





. (13)

Якщо

1K 

, тоді додатний числовий ряд







збігається. При

1K 

ряд розбігається. Якщо



, то треба застосовувати іншу

ознаку



Приклад 4. Дослідити збіжність ряду









Розв’язання. Застосуємо до заданого ряду радикальну ознаку

Коші

. Тоді

lim lim lim 0

nn n

  



 





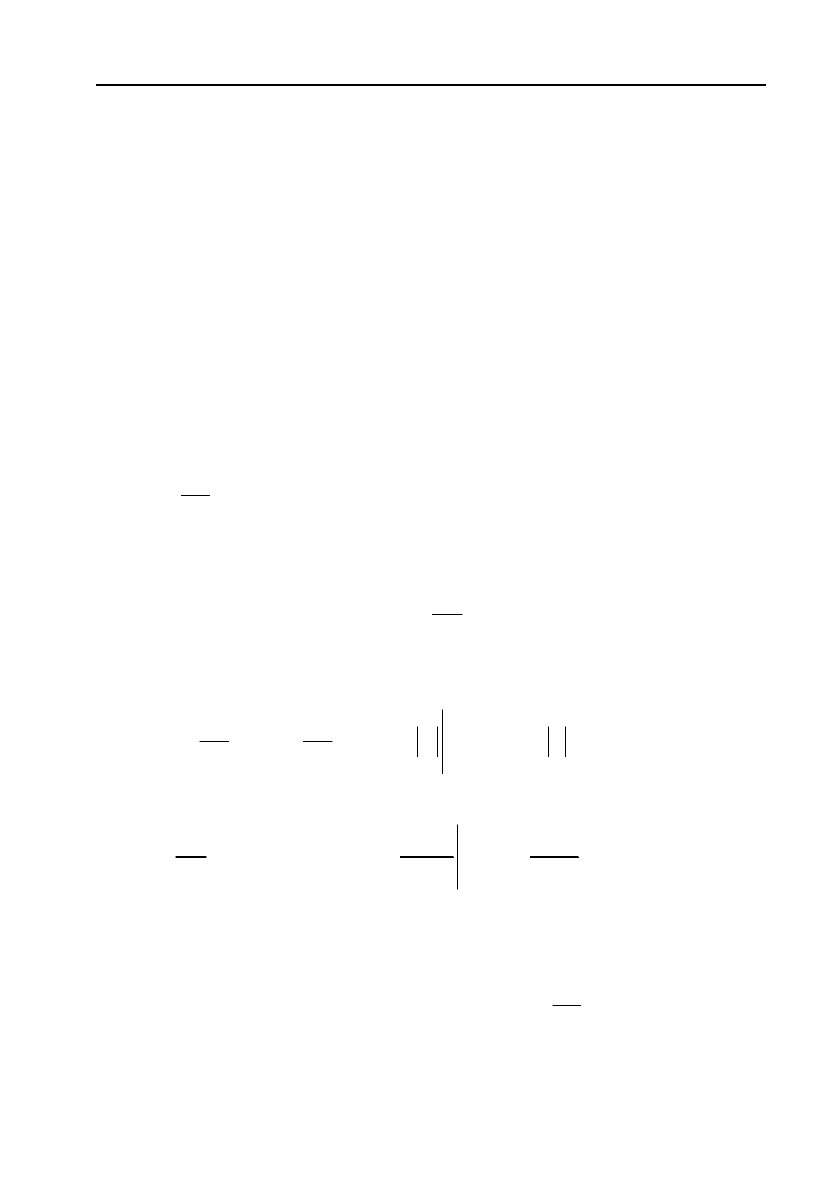
383

Частина 13. Числові та степеневі ряди

Отже, заданий ряд збігається.



Інтегральна ознака Коші. Треба дослідити збіжність додат&

ного числового ряду







, де



afn

. Розглянемо невласний інтег&

рал



xdx





. Якщо цей інтеграл збігається, то числовий ряд також

збігається

. Якщо цей інтеграл розбіжний, то числовий ряд також

розбіжний



Приклад 5. Дослідити збіжність узагальненого гармонічного

ряду









Розв’язання. Застосуємо до цього ряду інтегральну ознаку Коші.

Розглянемо невласний інтеграл





При



одержимо:



lim limln lim ln ln1

bb b

dx dx



  

  



В цьому випадку інтеграл розбіжний, отже і ряд розбіжний



lim lim lim 1

bbb

dx x

xdx b







  

 





Неважко бачити, що при



інтеграл є розбіжним, а при



інтеграл збіжний.

Отже, узагальнений гармонічний ряд







є збіжним, якщо



та розбіжним, якщо



384

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

13.1.5. Знакопочережні числові ряди



Означення 6. Ряд, члени якого почережно мають додатний та

від’ємний знаки, називають знакопочережним. Такий ряд можна

записати

, наприклад, у вигляді

 

1234

UUUUU U















(14)

U 

1, 2, 3,n 





Означення 7. Знакопочережний ряд називають збіжним аб

солютно

, якщо збігається додатний числовий ряд







, складений

абсолютних величин знакопочережного ряду (14).

Якщо ряд, складений з абсолютних величин членів ряду (14)

розбігається, а знакопочережний ряд збігається, то кажуть, що ряд

(14) збігається неабсолютно або умовно.

Абсолютну збіжність знакопочережного ряду досліджують з ви!

користанням достатніх ознак збіжності додатних числових рядів. Не!

абсолютну збіжність знакопочережного ряду досліджують з викори!

станням ознаки Лейбніца.



Ознака Лейбніца. Якщо абсолютні величини знакопочережно&

го ряду монотонно спадають, тобто

12 n

UUU U



і границя його загального члена дорівнює нулю при

n 

, тобто вико&

нується умова

lim 0





тоді знакопочережний ряд збігається, причому його сума

обов’язково

менша

першого члена ряду.

Якщо замінити суму цього ряду

його частковою сумою

тоді абсолютна величина похибки

буде менше першого відкину!

того члена ряду, тобто

1mm





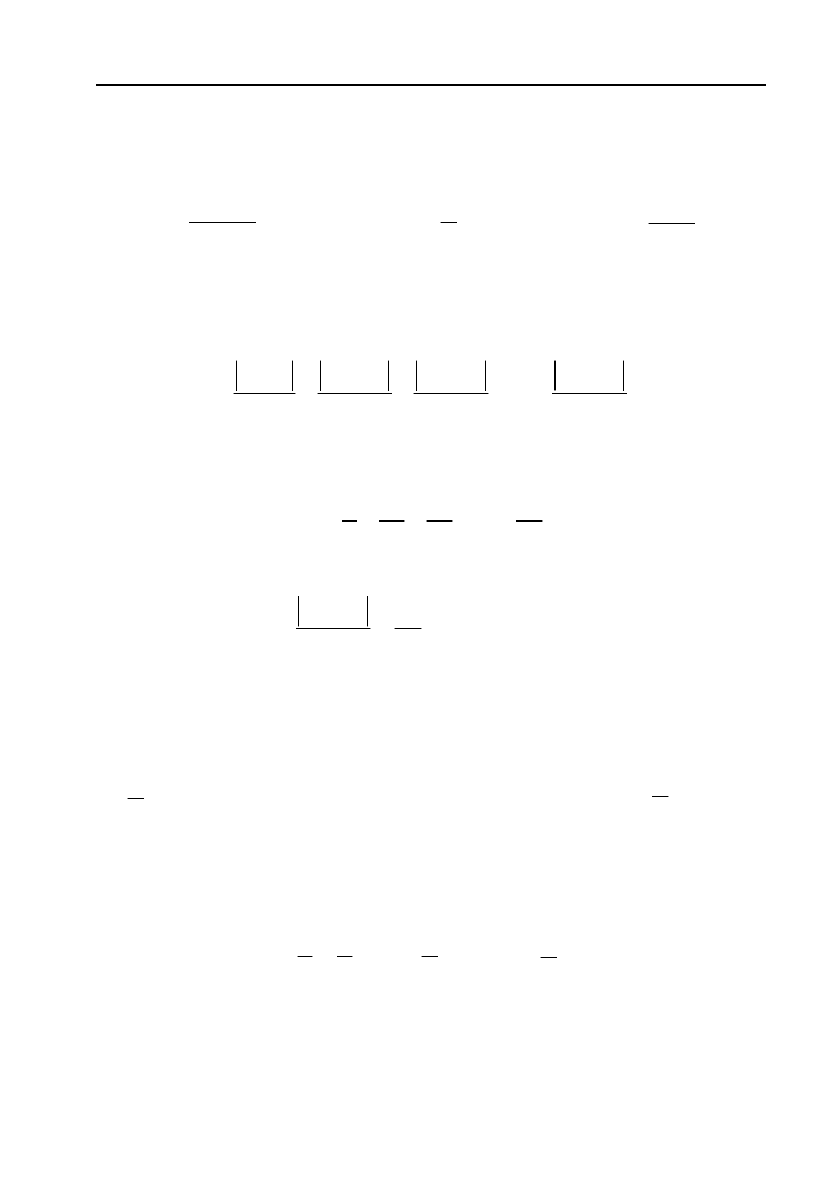
385

Частина 13. Числові та степеневі ряди

Остання оцінка використовується у наближених обчисленнях.



Приклад 6. Дослідити збіжність знакопочережних рядів:

а)

cos









; b)













; c)

















Розв’язання.

а) Складемо ряд з абсолютних величин заданого знакопочереж!

ного ряду (



— довільне число):

22 2

cos cos2 cos3 cos

12 3

 





(15)

Порівняємо цей ряд із збіжним узагальненим гармонічним ря!

дом

22 2

11 1 1

22 3 n





(16)

Кожний член ряду (15) менше або дорівнює відповідному члену

ряду

(16) тому, що

cos





1, 2, 3,n 



Згідно з ознакою порівняння ряд (15) збігається, а це означає,

що заданий знакопочережний ряд а) збігається абсолютно.

У цьому випадку ряд, складений з абсолютних величин







– розбіжний гармонічний ряд, тому ряд













абсолют!

но не збігається. Для дослідження його неабсолютної збіжності тре!

ба застосувати ознаку Лейбніца. У даному випадку обидві умови

ознаки

Лейбніца виконуються:

11 1

23 n

 



lim 0





Тому знакопочережний ряд b) збігається неабсолютно.

с) У цьому випадку не виконується необхідна умова збіжності

числового

ряду тому, що

386

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

lim 2 lim 2 0

 

 



Отже,















розбіжний.

13.1.6. Питання для самоперевірки

1. Як визначають числовий ряд, його часткову суму, суму ряду?

Який ряд називають збіжним, розбіжним? Які властивості ма!

ють збіжні числові ряди?

Як математично записати необхідну умову збіжності числово!

го ряду?

Який рад називають рядом геометричної прогресії? Коли цей

ряд

збігається, чому дорівнює його сума?

Який вигляд має і коли збігається узагальнений гармонічний

ряд

Як формулюються достатні ознаки збіжності додатних число!

вих рядів?

Які різновиди збіжності існують для знакопочережних число!

вих рядів?

Коли застосовуються і як формулюється ознака Лейбніца?

13.1.7. Вправи

1. Знайти загальний член ряду:

111

357





; b)

1111

2468





; c)

11 1

4916

 



;

34 5 6

491625

  



; e)

24 6 8

5 8 11 14

  



387

Частина 13. Числові та степеневі ряди

2. Записати перших 5 членів ряду та перевірити необхідну умову

збіжності

ряду:











; b)









; c)









;

















; e)







; f)









Дослідити збіжність ряду з використанням ознаки порівняння:









; b)









; c)







; d)









Дослідити збіжність ряду за ознакою Даламбера:









; b)









; c)



23 1









;







; e)









; f)



23 1









Дослідити збіжність ряду з використанням радикальної озна!

ки Коші:

















; b)















; c)















;

















; e)

15 1















Дослідити збіжність ряду за інтегральною ознакою Коші:







; b)









; c)











;











; e)









; f)









; g)







388

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

7. Дослідити збіжність знакопочережного ряду:













; b)













; c)













;













; e)













; f)















;





















13.2. Степеневі ряди

13.2.1. Радіус, інтервал та область збіжності



Означення 8. Степеневим рядом називають ряд вигляду

01 2

ax a ax ax ax





   





(17)

або

  

001 02 0 0

n n

axx a axx axx axx





  





, (18)

де



0,1,2,

an



— дійсні числа, які називають коефіцієнтами сте

пеневого ряду

— деяке постійне число.

Підстановка

xx

дозволяє ряд (18) звести до вигляду (17).

Тому нижче будемо розглядати лише ряди вигляду (17), тобто по

степенях



Теорема Абеля. (Нільс Генрік Абель (1802–1829) — норвежсь&

кий математик). Якщо ряд (17) збігається при

x

, то він

збігається абсолютно для усіх

, що задовольняють нерівність

xx

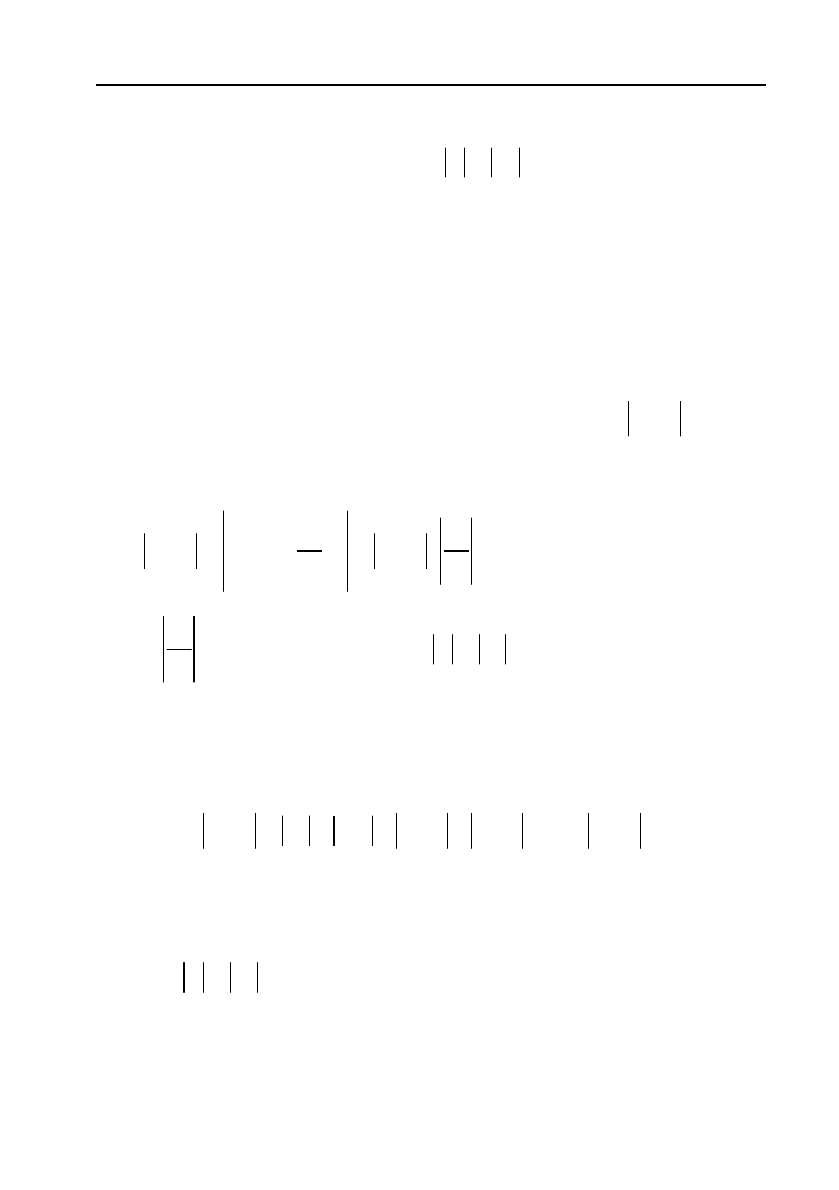
389

Частина 13. Числові та степеневі ряди

Якщо ряд (17) розбігається при

x

, то він розбігається для усіх

, які задовольняють нерівність

xx

Доведення. За умовою теореми ряд (17) при



xxx

збігається. Це означає, що збігається числовий ряд

01121 1

aaxax ax  

Але тоді загальний член цього ряду

ax 

при

n 

, тобто

загальний

член ряду є величина обмежена. Отже, існує таке число

0M 

, що при будь!яких

виконується нерівність

ax M

Тепер запишемо абсолютну величину загального члена ряду (17)

та оцінимо її:

nn n n

nn n

ax ax ax M q



  





0,1,2,3,n 



(19)

де



тому, що за умовою

xx

Запишемо два ряди: ряд, складений із абсолютних величин членів

ряду

(17) та ряд геометричної прогресії, загальним членом якого є

Mq

01 2 3

ax a ax ax ax ax





    





(20)

Mq M Mq Mq Mq





   





(21)

При

x

знаменник

ряду (21) менше одиниці, тому ряд

геометричної

прогресії (21) збігається. Згідно з нерівністю (19)

кожний член ряду (20) не більше відповідного члена ряду (21)

тому, за ознакою порівняння, ряд (20) збігається, а це означає, що

390

Барковський В.В., Барковська Н.В. «Вища математика для економістів»

ряд (17) збігається абсолютно. Отже, перше твердження теореми

доведено

Доведемо друге твердження теореми методом від супротивного.

Нехай ряд (17) збігається при

, які задовольняють нерівність

xx

. Тоді, згідно доведеному першому твердженню теореми, ряд

збігається

і при

x

, що суперечить умові другого твердження.

Отже, теорема повністю доведена.



Наслідок. Якщо степеневий ряд (17) збігається при

x

, то

цей ряд збігається в інтервалі



,xx



Означення 9. Додатне число

, таке, що при

R

степе&

невий ряд збігається, а при

R

ряд розбігається, називають ра

діусом збіжності степеневого ряду

. Інтервал



,RR називають

інтервалом збіжності цього ряду

Якщо степеневий ряд збігається при

xR

або при

xR

, або

при

xR

та

R

, тоді областю збіжності цього степеневого ряду

буде

[

)

RR

або

(

]

RR

, або

[

]

RR

, відповідно.

Радіус збіжності повного степеневого ряду знаходять за форму!

лами:

lim







(22)

або

lim





. ( 23)



Приклад 7. Знайти області збіжності рядів:

 

xxx x







 





;