Барков Ю.А., Зверев О.М., Перминов А.В. Сборник задач по общей физике

Подождите немного. Документ загружается.

5. Момент инерции платформы – диска

ImR

момент инерции человека – материальной точки

= 0; I′

= m

Угловая скорость платформы ω до перехода человека

ω = 2πn.

6. Подставим выражения I

, I

, I′

и ω в формулу (3)

0,5

vnR

mR mR

и упростим:

2π

vRn

Подставляем числовые значения величин:

180 1

23,14 1,5 1

180 2 60 6

v =⋅⋅⋅⋅=

+⋅

№ 3.

На краю диска, масса которого m и радиус R, стоит че-

ловек массой M. Диск совершает вращательное движение с часто-

той n об/с. Чему равна кинетическая энергия системы? Чему равна

работа внешних сил, в результате действия которых частота враще-

ния увеличивается вдвое?

Р е ш е н и е.

Запишем формулу кинетической энергии вращающегося тела:

E = (1)

где I – момент инерции системы; ω – угловая скорость вращения

системы.

Выразим момент инерции системы I и угловую скорость ω.

Момент инерции системы складывается из моментов инерции тел

системы:

I = I

+ I

где I

– момент инерции диска, I

; I

– момент инерции чело-

века, I

. Угловая скорость ω = 2πn. Подставим выражения I

и I

в формулу (1):

222 222

4π 4π

(2π

)(2).

222 4

II mR n R n

EnMRmM



==+=+





22 2

(2)

EnRmM

=+. (2)

Работу сил определяем по теореме об изменении кинетиче-

ской энергии:

к2 к1

EE A

−=

∑

Используя уравнение (2) и условие n

= 2n

, запишем:

А = π

(m + 2M) – π

(m + 2M) = 3π

(m + 2M).

1.4. ГИДРОМЕХАНИКА

Основная задача гидромеханики состоит в том, чтобы найти

законы распределения давлений и скоростей внутри жидкости.

Сравнительно просто эта задача решается для идеальной несжи-

маемой жидкости, в которой отсутствуют силы трения между ее

слоями (нет вязкости). Со стороны идеальной жидкости на тела мо-

гут действовать только нормальные силы упругости.

Задачи, связанные с нахождением давлений и сил давления

в какой-либо точке внутри жидкости, решаются на основании зако-

на Паскаля и вытекающих из него следствий. К ним можно отнести

задачи на сообщающиеся сосуды. Порядок их решения может быть

следующим:

1. Сделать схематический чертеж и отметить равновесные уров-

ни жидкости, которые она занимает по условию задачи. Если даны со-

общающиеся сосуды с разнородными жидкостями, то нужно отметить

уровни каждой из них. Затем следует выбрать поверхность нулевого

уровня, от которого будут отсчитываться высоты столбов всех жидко-

стей. Эта поверхность должна проходить через однородную жидкость;

обычно ее выбирают на нижней границе раздела сред (жидкость –

жидкость, жидкость – воздух) или на уровне трубки, соединяющей

сосуды. Если по условию задачи происходит перетекание жидкости из

одного сосуда в другой и при этом имеется два или несколько равно-

весных состояний жидкостей, то необходимо отметить высоты всех

уровней, отсчитывая их от поверхности нулевого уровня.

Указав высоты столбов всех жидкостей в сосудах относи-

тельно поверхности нулевого уровня, следует записать уравнение

равновесия жидкостей.

Составив уравнение равновесия, следует, при необходимо-

сти, дополнить его условиями, которые связывают между собой вы-

соты h

, h

и т.д. Например, если жидкость перетекала из одного

сосуда в другой, то обычно в качестве дополнительного условия

используется свойство несжимаемости жидкостей: при уменьшении

объема жидкости в одном из сосудов объем этой жидкости в другом

сосуде увеличивается на такую же величину. Совместное решение

полученных уравнений позволяет найти искомые величины.

В другую группу задач можно выделить задачи на примене-

ние силы Архимеда при плавании или движении тел в жидкости.

Принципиально решение таких задач не отличается от решения за-

дач статики и динамики. Здесь, кроме сил, рассмотренных в под-

разд. 2.2, должна быть учтена сила Архимеда.

Основные формулы

1. Давление, производимое силой F, равномерно распреде-

ленной по плоской поверхности площадью S и действующей пер-

пендикулярно поверхности, находим следующим образом:

⊥

= .

2. Давление, создаваемое покоящейся жидкостью, называют

гидростатическим.

При отсутствии движения внутри идеальной жидкости, нахо-

дящейся в равновесии, давление, производимое жидкостью на глу-

бине h, вычисляется по формуле:

p = ρgh,

где ρ – плотность жидкости; g – модуль ускорения свободного

падения.

Формула носит общий характер: давление не зависит от того,

какую форму имеет сосуд, содержащий жидкость.

На тело, погруженное в жидкость, действует выталкивающая

сила, модуль которой равен весу жидкости, вытесненной телом:

= ρ

gV,

где ρ

– плотность жидкости; V – объем вытесненной жидкости.

Уравнение Бернулли:

const.

gh p++=

Примеры решения задач

№ 4.

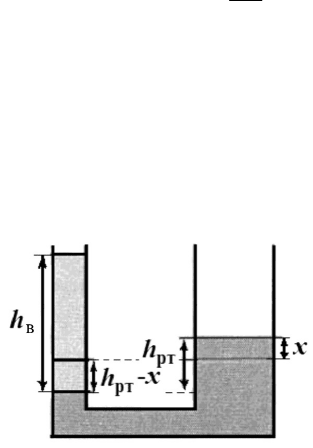
В сообщающихся сосудах находится ртуть. Площадь се-

чения одного сосуда в 2 раза больше, чем другого. В узкий сосуд

наливают столб воды высотой 1,02 м. На сколько миллиметров

поднимется ртуть в широком сосуде? Плотность ртути 13600 кг/м

Р е ш е н и е.

Приравнивая давления в со-

судах на уровне границы ртути

с водой, придем к уравнению

рт

· h

рт

= ρ

· h

Обозначив за x изменение

уровня ртути в широком сосуде,

запишем условие неизменности

объема ртути:

2S · x = S(h

рт

– x)

(

увеличение объема ртути в широком сосуде равно уменьшению

в узком сосуде). Решая совместно эти уравнения, получаем:

вв

рт

3ρ

x ==

25 · 10

–3

м = 25 мм.

№ 5. Однородное тело плавает на поверхности керосина (ρ

800

кг/м

) так, что объем погруженной части составляет 0,92 всего

объема тела. Определить объем погруженной части при плавании

тела на поверхности воды.

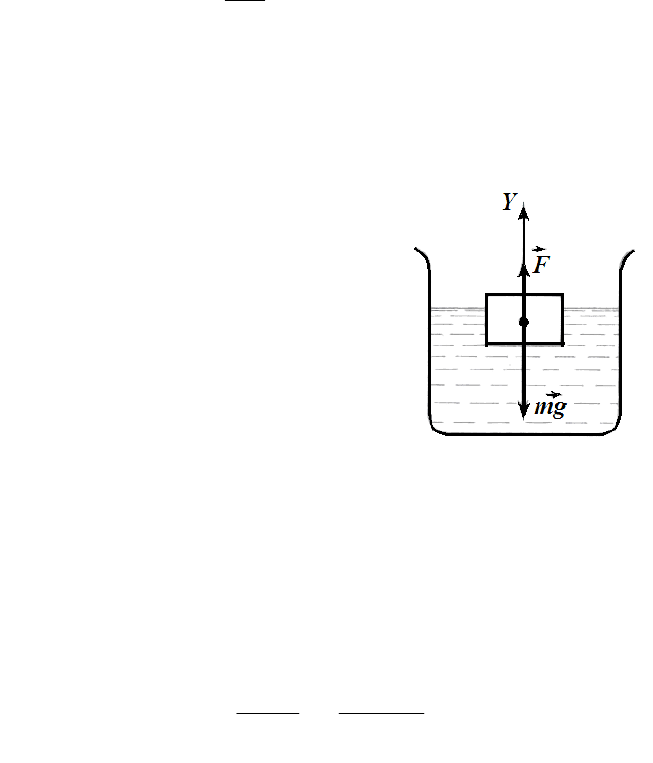
Р е ш е н и е.

Обозначим: V – объем всего тела;

– объем погруженной части тела,

плавающего в керосине;

– объем по-

груженной части тела, плавающего в во-

де. На тело, плавающее в керосине, дей-

ствуют: mg – сила тяжести; F = ρ

·g –

сила Архимеда. Из условия плавания

следует, что mg = F, или

кП к

ρρ

0,92 ,

mg V g V g

=⋅⋅=⋅ ⋅⋅ (1)

где ρ

– плотность керосина.

Аналогично запишем условие плавания тела в воде:

mg = F

или

вП

mg V g

=⋅⋅

(2)

где ρ

– плотность воды.

Из уравнений (1) и (2) получим:

квП

ρ 0,92 ρ

Vg V g

⋅⋅⋅=⋅⋅,

откуда

0,92ρ 0,92 800

0,74 .

ρ 1000

VV VV

⋅

== ≈⋅

Варианты заданий приведены на стр. 182–213.

1.5. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ

Колебательным называется такое движение, при котором те-

ло многократно проходит одно и то же устойчивое положение рав-

новесия. Если при этом оно возвращается в исходное положение

через равные промежутки времени, то такие колебания называют

периодическими. Если в периодических колебаниях изменения всех

физических величин происходят по закону синуса (или косинуса),

то такие колебания называются

гармоническими, а частица, совер-

шающая гармонические колебания, называется

гармоническим ос-

циллятором. Простейшей колебательной системой с одной степе-

нью свободы является линейный осциллятор, описываемый диффе-

ренциальным уравнением

′′

+=.

В данной системе реализуются гармонические колебания вида

x = A · sin(ω

· t + α),

где

А – амплитуда колебаний; ω

– циклическая частота; α – началь-

ная фаза.

Задачи данного подраздела можно условно разделить на три

группы: задачи, требующие применения общих уравнений гармо-

нических колебаний и задачи на сложение колебаний; задачи о ма-

тематических и физических маятниках и задачи о распространении

механических колебаний в пространстве, т.е. волн.

При решении задач

первой группы следует обратить особое вни-

мание на составление дифференциального уравнения для точки, совер-

шающей гармонические колебания. Это уравнение в конечном итоге

приводит к соотношению k = m⋅ω

, в котором коэффициент k должен

быть выражен через те или иные величины, характеризующие колеба-

тельную систему. Нахождение выражения для этого коэффициента фак-

тически и представляет основное содержание задач такого типа.

Для решения задач на сложение колебаний одного направле-

ния достаточно часто используется метод вращающегося вектора

амплитуды (метод векторных диаграмм), когда складываемые коле-

бания изображаются в виде двух векторов, и амплитуда и фаза ре-

зультирующего колебания находятся по теореме косинусов.

При решения задач на сложение взаимно перпендикулярных

колебаний для нахождения траектории результирующих колебаний

можно воспользоваться уравнением эллипса:

cosφ

sin

xxy y

AAB B

−+=.

В этом случае наибольшую сложность представляет опреде-

ление φ

– разности фаз складываемых колебаний. При этом надо

помнить, что складываемые колебания должны иметь одинаковую

частоту. В некоторых случаях задачи данного типа решаются с ис-

пользуем формул тригонометрии.

При решении задач

второй группы нужно представлять, что

при ускоренном движении точки подвеса математического маятни-

ка изменяется сила натяжения нити, что приводит к изменению

равнодействующей силы и, следовательно, частоты и периода коле-

баний. Формулу периода колебаний легко получить для каждого

конкретного случая, внося соответствующую поправку в формулу

периода математического

маятника:

2π

= ,

где l – длина подвеса; a – модуль ускорения, сообщаемого грузу си-

лой натяжения нити. Если маятник в том или ином направлении

приобретает переносное ускорение

, то

aga

=−

GGG

. Найдя обыч-

ными методами модуль этого ускорения и подставив его в приве-

денную выше формулу, получим выражение для периода колебаний

математического маятника с учетом движения точки подвеса.

Что касается задач на физический маятник, то здесь нужно

хорошо знать понятие приведенной длины физического маятника,

которая зависит от момента инерции маятника и расстояния между

точкой подвеса и центром тяжести.

Решение задач

третьей группы сводится обычно к записи

уравнения плоской волны и соотношения между длиной волны и

скоростью ее распространения, что дает возможность определить

фазу (разность фаз) или смещение точки

от положения равновесия

в произвольный момент времени.

Основные формулы

1. Связь между периодом, циклической частотой и частотой:

2π 1

ων

T ==

2. Кинематические характеристики колебательного движения:

– путь (смещение) x = A · sin(ω

· t + φ

);

– скорость v = A· ω·cos(ω

·t + φ

), максимальная скорость:

max

= A·ω;

– ускорение

а = A·ω

·sin(ω

·t + φ

), максимальное ускорение:

max

= A·ω

3. Динамические характеристики колебательного движения:

– сила F = ma = m·A·ω

·sin(ω

·t + φ

);

– кинетическая энергия

()

22 2 2

cos

ωφ

mA t

⋅+

== ;

– потенциальная энергия

()

22 2 2

000

sin

ωφ

mA t

⋅+

;

– полная энергия

⋅

4. Период колебаний математического маятника

2π

5. Период колебаний физического маятника

2π 2π

gmbg

⋅⋅

где I – момент инерции; b – расстояние от точки подвеса до центра

тяжести; L – приведенная длина.

6. Сложение колебаний:

а) сложение колебаний одинаковой частоты, направленных

вдоль одной прямой:

– амплитуда результирующего колебания

()

12 12 21

2cosφφ

AAA AA=++ −

– начальная фаза результирующего колебания

112 2

sinφ

sin

arctg ,

cosφ

cos

где

и А

– амплитуды складываемых колебаний, φ

и φ

– началь-

ные фазы складываемых колебаний;

б) сложение взаимно перпендикулярных колебаний:

x = A·sin ωt, y = B·sin(ωt + φ

);

уравнение эллипса

cos

sin

xxy y

AAB B

−+=

7. Затухающие колебания:

– уравнение x = A

·e

–βt

·sin(ωt + φ

), где β – коэффициент за-

тухания;

– период затухающих колебаний

2π 2π

ωβ

T ==

−

;

– время релаксации

= ;

– декремент затухания

()

At T

⋅

;

– логарифмический декремент затухания δ = lnσ = β · T.

8. Вынужденные колебания:

– амплитуда

()

22 22

ωω

βω

B =

−+

начальная фаза

2βω

arctg ,

ωω

−

где

= F

– амплитуда вынуждающей силы; ω

– циклическая

частота собственных колебаний; ω – циклическая частота вынуж-

денных колебаний;

– резонансная частота

рез 0

ωω

;

=−

–

резонансная амплитуда

рез

2βω β

A =

−

9. Уравнение плоской бегущей незатухающей волны:

2π

sin ω

xA t l



=−





10. Вектор Умова:

pwv

=⋅

где w – объемная плотность энергии; v – скорость распространения

волны. Его модуль равен энергии, переносимой волной за единицу

времени через единичную площадку, расположенную перпендику-

лярно направлению распространения волны.

Примеры решения задач

№ 1.

Материальная точка массой m = 0,01 кг совершает гар-

монические колебания по закону синуса с периодом Т = 2 с и на-

чальной фазой ϕ

, равной нулю. Полная энергия колеблющейся

точки W = 0,1 мДж.

Требуется: найти амплитуду А колебаний; написать закон

данных колебаний x = f (t); найти наибольшее значение силы F

max

действующей на точку.

Р е ш е н и е.

Записываем закон гармонических колебаний

x = A sinωt.

Так как закон не дает возможности определить амплитуду А,

следует обратиться к условию задачи и воспользоваться полной

энергией Е. Полная энергия колеблющейся точки Е равна, напри-

мер, ее максимальной кинетической энергии W

к,max

max

к,max

WW==