Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.


222
где
nnn3n2n1
2n232221
1n131211
1-
cccc
cccc
cccc
= A=C
L
LLLLL
L
L
-
обращенная
матрица
, c
ij
-
элементы
обра
-
щенной
матрицы
.
Искомые
температуры
находятся
из
уравнений
:
.t=bc + bc+ bc+ bc
t=bc + bc+ bc+bc
t=bc + bc+ bc+ bc
nnnn3n32n21n1
2n2n323222 121
1n1n313212111
L
LLLLLLLLLLLLLL
L
L
Отметим
,
что
существуют
стандартные
программы
обращения
матриц
,
напи
-
санные
для
основных
языков
программирования
(
см
.
Приложение
II).
Явный
метод
решения
задач
нестационарной
теплопроводности
Критерий
устойчивости
а
.
Узел
находится
внутри
тела
.
Если
при
рассмотрении
стационарной
теплопроводности
сумма
тепловых
по
-
токов
от
соседних
узлов
к
текущему
равна
нулю
, 0
0i
∑
=
→
Q
&
то
при
нестацио
-
нарном
режиме
поступающий
в
узел
тепловой
поток
идет
на
изменение
энталь
-
пии
вещества
во
времени
∑
=
→
∂τ
∂
0
0i
I
Q
&
.
Переходя
от
дифференциального
уравнения
к
записи
в
конечных
разностях
при
y
x
∆
=
∆
,
получим
(
см
.
рисунки
предыдущего
параграфа
)
(
)
(
)
(
)
(
)
(
)
τ
ρλλλ
τττ
ττττ
∆
∆=
∆
∆++
∆
∆+
∆
∆+
∆
∆
∆
0004030201
λ
-TT
xbc
x
-TT
xb
x
-TT
x b
x
-TT
x b
x
-TT
x b
+
2
где
надстрочный
индекс
τ
определяет
момент
времени
.
Разделим
уравнение
на
λ
:
( ) ( ) ( ) ( )
(
)
τ
ττττττ
τλ
ρ
0
+
0
2
04030201
-
c
---- TTxTTTTTTTT
∆
∆
∆
=+++ .
Вводя
критерий
Фурье
=
∆
∆
=
∆⋅
∆
=∆
∆
ρ
λ
τ
τ
ρ
λ
τλ
ρ
=
Fo
11
c
2
2
2
c
a
x
a
c
x
x ,
получим
(
)
ττττ
τ
0
+
004321
-Fo4Fo+++ TTTTTTT
∆
=−⋅
.
Последнее
уравнение
разрешим
относительно
температуры
в
узле
на
новом
временном
шаге
τ
+∆
τ
(
)
(
)
Fo41Fo+++=
04321
+
0
−+⋅
∆
τ
τ
ττ
TTTTTT
. (18.5)
Искомая
температура
будет
отвечать
реальному
значению
,
если
коэффициент
при
τ
0
T
положителен
или
равен
нулю
,
т
.
е
.
4
1
Fo ≤ .
Последнее
неравенство
можно
рассматривать
как
критерий
устойчивости
численного
решения
.
б
.
Узел
находится
на
поверхности
(
)
(
)
(
)
( )
=∆+
∆
∆
+
∆
∆
+
∆
∆
τ
τττ
αλλλ
0
ж
030201
-
-
2
-
2
-
TTxb
x
TT
x
b
x
TT
x
b
x
TT
xb
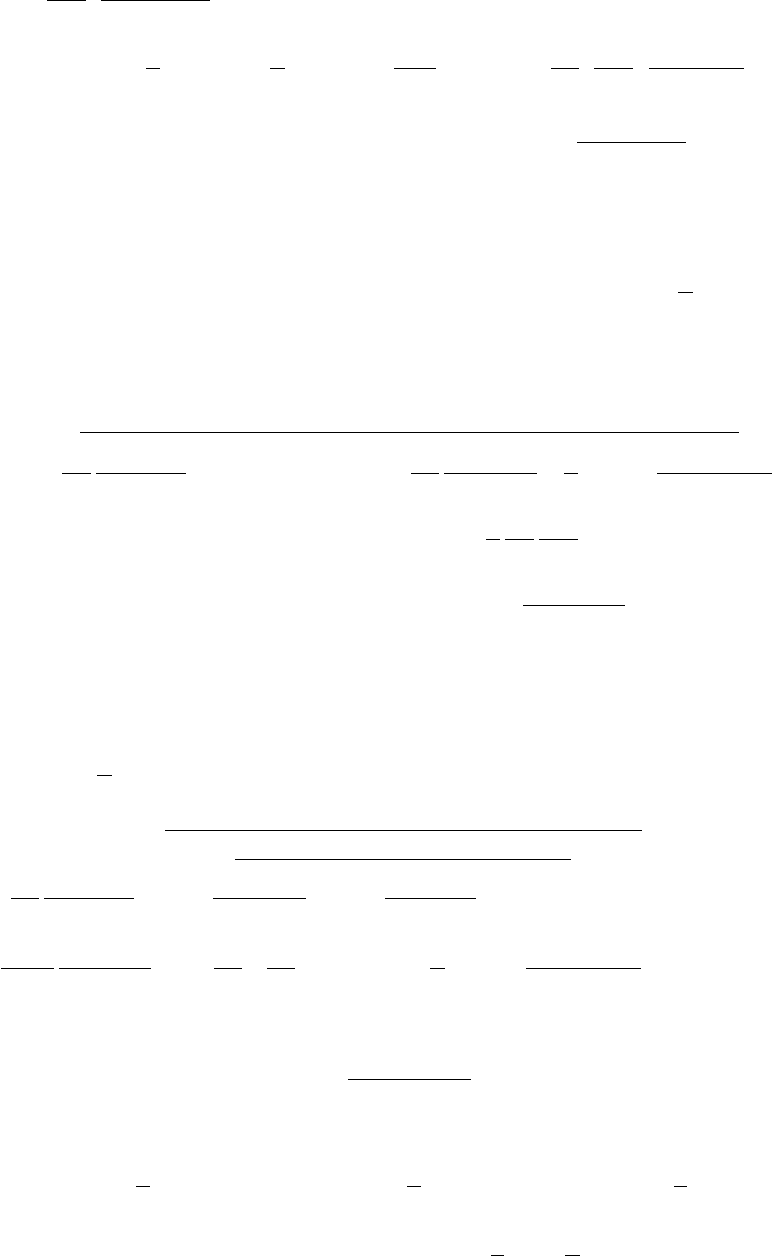
223
(
)
τ
ρ
τττ
∆
⋅
∆
=
∆
0
+
0
2
-
2
TT
x
bc .
( ) ( ) ( ) ( )
,
-
2
c
--
2
1
-
2
1
-
0
+
0
2
0
ж
030201
∆
∆
⋅=
∆
+++
∆
τλ
ρ
λ
α
τττ
ττττ
TT
x
TT
x
TTTTTT
(
)
F
о
-
=2Bi-2Bi+-+-+2-2
0
+
0
0
ж
030201
τττ
ττττττττ
TT
TTTTTTTT
∆
,
(
)
ττττττ
τ
∆
+−+−
+
000
ж
0321
=BiFо2BiFo2Fо4Fо++2 TTTTTTTT ,
(
)
)( )
τ
τ
ττ
0
ж
321
+
0
BiFо(221FoBi2++2= TTTTTT +−+⋅+
∆
. (18.6)
Для узлов этого типа критерий устойчивости имеет вид
( )
2
1
Bi2Fo ≤+ .
Если поверхность теплоизолирована, то в уравнении (18.6) следует поло-
жить Bi=0.
в. Узел образует внешний угол при граничных условиях III рода
(
)
( )
(
)
(
)
τ
ρλαλ
τττ
τ
τ
τ
∆
−
∆=
∆
−
∆
+−∆+
∆
−
∆
∆+
00
2
02
0
01
4
1
2
2
TT
bxc
x
TT
x
bTTxb
x
TT
x
b
ж
( ) ( ) ( )
( )
τττ
τττ
τλ
ρ
00
2
00201
2
1
2 TT
xc
TTBiTTTT
ж
−
∆
∆
=−+−+−
∆+
,
( )
Fо
2
Bi22Bi2
00
0021
τττ
ττ
τ
TT
TTTTT
ж
−
=−−++
∆+
(
)
( ) ( )( )
(18.7).Bi1Fo41Bi2Fo2
FoBi4Fo4Bi2Fo2
021
000210
+−+++=
=+−−++=
∆+
τ
τ
τττ
τ
ττ
TTTT
TTTTTTT
ж
ж
Чтобы решение было устойчивым, необходимо выполнение условия
( )
4
1
Bi1Fo ≤+ .
г. Узел находится в вершине внутреннего угла
при граничных условиях III рода
(
)
(
)
(
)
( )
( )
( )
.
4
3
222
2
00
2
0
04
030201
τ
ρα
λ
λλλ
τττ
τ
τ
τττ
∆
−
∆=−
∆
+
∆
+
∆
−
∆
+
+
∆
−
∆+
∆
−
∆+
∆
−
∆
∆+
TT
xbcTT
xx
b
x
TT
xb
x
TT
xb
x
TT
xb
x
TT
x
b
ж
(
)
(
)
(
)
(
)
( )
( )
.
Fo2
3
Bi2
22
00
0
04030201
τττ
τ
ττττ
TT
TT
TTTTTTTT
ж
−
=−+
+−+−+−+−
∆+
(
)
(
)
ττττττ
τ
00003241
33BiFo4Fo12BiFo42Fo2 TTTTTTTTT
ж
−=−−++++
∆+
( )( )
+−+++++=
∆+
Bi
3
1
1Fo41BiFo
3
4
2Fo
3
2
032410
ττ
τ
ττ
TTTTTTT
ж
(18.8)
4
1
Bi
3
1
1Fo ≤
+
. (*)
Если внутренний угол теплоизолирован, то необходимо положить Bi=0. При-
менение уравнения (18.8) для узла в момент
(
)
τ
τ
∆
+
реали зует явный метод.
При решении задачи явным методом необходимо выполнять условие
224
устойчивости (*), если это условие не выполняется, то полученные значения температур
не будут отвечать действительным.
Неявный метод решения задач нестационарной теплопроводности
В этом методе разностные уравнения записываются для температур в момент
(
)
τ
τ
∆
+
.
Рассмотрим, например, узел на поверхности тела при граничных условиях III рода:
( )
( )
.
2
1
22
00
2
0
030201
τ
ρα
λλλ
τττ
ττ
ττττττ
∆
−
∆=−∆+
+
∆
−
∆
+
∆
−
∆
+
∆
−
∆
∆+
∆+
∆+∆+∆+
TT
xbcTTxb
x
TT
x
b
x
TT
x
b
x
TT
xb
ж
Так
как
значения
температур
на
шаге
τ
+
∆
τ
неизвестны
,
то
для
того
,
чтобы
задача
была
замкнутой
,
следует
решать
систему
с
числом
уравнений
,
равным
числу
узлов
.
Неявный
метод
всегда
устойчив
,
точность
определения
температуры
зависит
от
выбора
шагов
x
∆
и
τ
∆
.
19. Конвективный теплообмен в однородной среде
Основные
понятия
и
определения
Теория
конвективного
теплообмена
изучает
теплоотдачу
между
телом
и
окружающей
его
жидкостью
при
их
движении
.
В
основе
описания
теплоотдачи
лежит
эмпирический
закон
Ньютона
-
Рихмана
:
(
)
∞
−= TTq
с
α
,
Вт
/
м
2
,
где
под
Т
∞
понимается
температура
жидкости
в
невозмущенном
потоке
.
Рис
.19.1
Около
обтекаемого
жидкостью
тела
(
рис
.19.1)
образуется
гидродинамический
пограничный
слой
,
в
котором
скорость
потока
жидкости
меняется
от
значения
скорости
на
бесконечности
W
∞
до
W
=0
на
поверхности
(
так
называемый
эффект
прилипания
).
Практически
считают
,
что
толщина
пограничного
слоя
(
)
x
δ
равна
расстоянию
от
стенки
,
на
котором
скорость
жидкости
составляет
0,99
W
∞
.
Аналогично
гидродинамическому
,
вводят
понятие
теплового
пограничного
слоя
,
внутри
которого
температура
меняется
от
t
∞
до
t
с
.
Вне
теплового
пограничного
слоя
0=
∂
∂
y
t
.

225
Если
в
твердых
телах
плотность
теплового
потока
определяется
законом
Фурье
Tq grad
λ
−=
r
,
то
в
движущихся
средах
необходимо
учесть
,
кроме
того
,
перенос
теплоты
потоком
→→
+−= wiTq
ρλ
grad ,
Вт
/
м
2
,
где
первое
слагаемое
описывает
перенос
теплоты
теплопроводностью
(
на
молекулярном
уровне
),
а
второе
-
конвекцией
(
поток
вещества
переносит
энтальпию
).
На
теплоотдачу
оказывают
влияние
коэффициент
объемного
расширения
и
коэффициент
изотермического
сжатия
жидкости
.
Коэффициент
объемного
расширения
:
p
T
∂
∂
−=
ρ
ρ
β
1
, (19.1)
для
идеального
газа
:
RT
p
=
ρ
,
2
RT
p
T
p
−=
∂
∂
ρ
. (
а
)
Подставим
(
а
)
в
(19.1):
1
2
TRT
p
p
RT
==
β
К
-1
,
то
есть
T
1
ид.газа
=
β
.
Коэффициент
изотермического
сжатия
:
1
T
p
∂
∂
=
ρ
ρ
ε
Па
-1
. (19.2)
Для воды ε=5⋅
110
10
−−
Πа . У воздуха при нормальных условиях ε=10⋅
15
−
−
Π
а
Таким образом, сжимаемость воздуха больше сжимаемости воды в 20 тысяч раз.
Если скорость газа не больше 0,3 термодинамической скорости звука , то поток
можно считать несжимаемым.
Основные уравнения сохранения
Уравнение сплошности
Получим уравнение сплошности для однородной среды. Выделим в бесконечной
изотропной среде неподвижный объем V (рис.19.2) .
Изменение плотности
ρ
в фиксированном объеме в единицу времени
∫
V
dV
∂τ
∂ρ
возможно
за счет потока вещества через поверхность F, ограничивающую объем V, то есть:
dFnw
F
ρ
∫
⋅−
r
r
, здесь знак “-” обусловлен тем, что вектор w
r
имеет направление,
противоположное направлению единичного вектора
r
n
элементарной площадки dF.
Таким образом,
∫ ∫
⋅−=
V F
dFnwdV
ρ
∂τ
∂ρ
rr
, или
dVdFw
VF
n
∫∫
∂
∂
=−
τ
ρ
ρ
. (а)
По теореме Остроградского-Гаусса поток вектора через поверхность F равен дивергенции
этого вектора, взятой по объему, ограниченному данной поверхностью
(
)
∫∫
=
VF
n
dVwdivdFw
v
ρρ
.
(в)
Подставим (в) в (а):
( )
dVdVwdiv
VV
∫∫
∂
∂
=−
τ
ρ
ρ
r
, или
( )
∫
=
+
∂
∂
V
dVwdiv 0
r
ρ
τ
ρ
.
Приравнивая нулю подынтегральное выражение (т.к. dV≠0), получаем искомое уравнение
сплошности в дифференциальном виде
( )
0=+
∂
∂
wdiv
r
ρ
τ
ρ
. (19.3)

226
Уравнение движения
В курсе гидрогазодинамики на основе
положения о том, что сила инерции элементарного
объема уравновешивается суммой всех действующих
на него внешних сил, выводится уравнение
движения, векторная форма записи которого имеет
вид
+
d
D
2
→→
→
∇−∇= F +wp
w
µ
τ
ρ
. (19.4)
Первое слагаемое в правой части описывает силы
давления, второе - силы вязкости, третье - объемные
(массовые) силы. Однако векторная форма есть лишь
краткая форма записи уравнения. Чтобы решить его,
следует найти все составляющие скорости (в декартовой системе координат это
zyx
www и, ), а для этого следует записать проекции уравнения движения на координатные
оси.
Так как в общем случае
( )
x, y,z=f w ,
τ
→
, запишем
→
wd
как дифференциал функции четырех
переменных
dz
z
w
dy+
y
w
dx+
x
w
d
w
=wd
∂
∂
∂
∂
∂
∂
τ
∂τ
∂
→→→→
→
+
, тогда выражение для полной или
субстанциональной производной принимает вид
zd
D
∂
∂
∂
∂
∂
∂
∂τ
∂
τ
→→→→→
+++=
w
w
y
w
w
x
w
w
ww
zyx
.
Здесь
∂τ
∂
→
w
характеризует
локальное
изменение
скорости
как
функцию
времени
,
остальные
слагаемые
определяют
конвективное
изменение
скорости
,
связанное
с
движением
частицы
в
пространстве
.
Представим
уравнение
(19.4)
после
деления
на
ρ
в
виде
системы
трех
уравнений
-
проекций
на
оси
декартовых
координат
:
проекция
на
ось
х
+
ρ
1
=
x
p
z
w
w
y
w
w
x
w
w
w
x
z
x
y
x
x
x
∂
∂
∂
∂
∂
∂
∂
∂
∂τ
∂
−+++
x
xxx
+g
z
w
+
y
w
+
x
w
2
2
2
2
2
2
+
∂
∂
∂
∂
∂
∂
ν
,
проекция
на
ось
у
+
ρ
1
=
y
p
z
w
w
y
w
w
x
w
w
w
y
z
y
y
y
x
y
∂
−+++
∂
∂
∂
∂
∂
∂
∂
∂τ
∂
y
2
y
2
2
y
2
2
y
2
+ g
z
w
+
y
w
+
x
w
+
∂
∂
∂
∂
∂
∂
ν
,
проекция
на
ось
z
+
ρ
1
=
z
p
z
w
w
y
w
w
x
w
w
w
z
z
z
y
z
x
z
∂
−+++
∂
∂
∂
∂
∂
∂
∂
∂τ
∂
z
2
z
2
2
z
2
2
z
2
+ g
z
w
+
y
w
+
x
w
+
∂
∂
∂
∂
∂
∂
ν
.
Запись
в
виде
уравнений
в
проекциях
на
оси
выбранной
системы
координат
используется
при
решении
уравнения
движения
,
например
,
одним
из
численных
методов
.
Рис
.19.2
227
Уравнение
энергии
При
рассмотрении
задач
теплопроводности
,
мы
получили
уравнение
энергии
в
виде
:
→
−= q
i
div
∂τ
∂
ρ
. (19.5)
В
задачах
конвективного
теплообмена
плотность
теплового
потока
имеет
две
составляющие
-
за
счет
теплопроводности
и
за
счет
конвекции
k
qq=q
→→→
+
λ
→
w T + i
ρλ
grad -= . (19.6)
Запишем
дивергенцию
вектора
q
r
z
q
y
q
x
q
=q
z
y
x
∂
∂
∂
∂
∂
∂
++
→
div . (a)
С
учетом
(19.6)
при
постоянных
λ
и
ρ
:
xx
iw +
x
T
q
ρ
∂
∂
λ
−=
,
yy
iw +
y
T
q
ρ
∂
∂
λ
−=
,
zz
iw +
z
T
q
ρ
∂
∂
λ
−=
,
тогда
−=
x
i
+w
x
w
i +
x
T
x
q
x
x
2
2
x
∂
∂
∂
∂
ρ
∂
∂
λ
∂
∂
,
−=
y
i
+ w
y
w
i +
y
T
y
q
y
y
2
2
y
∂
∂
∂
∂
ρ
∂
∂
λ
∂
∂
, (
в
)
−=
z
i
+ w
z
w
i +
z
T
z
q
z
z
2
2
z
∂
∂
∂
∂
ρ
∂
∂
λ
∂
∂
,
+ div
→
2
2
2
2
2
2
z
T
+
y
T
+
x
T
=-q
∂
∂
∂
∂
∂
∂
λ
+
z
i
+w
y
i
+w
x
i
w +
z
w
+
y
w
+
x
w
i
zyx
z
y
x
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
ρ
. (
с
)
Уравнение
сплошности
0 div +
=
→
w
ρ
τ∂
ρ∂
при
ρ
= const
принимает
вид
0 div
=
→
z
w
+
y
w
+
x
w
= w
z
y
x
∂
∂
∂
∂
∂
∂
. (d)
Подставим
(
с
)
в
(19.5)
с
учетом
(d):
( )
++=
2
2
2
2
2
2
zyx
z
T
y
T
x
T
z
i
+w
y
i
+ w
x
i
+w
i
∂
∂
∂
∂
∂
∂
λ
∂
∂
∂
∂
∂
∂
τ∂
∂
ρ
,
или
в
векторной
форме
Tiw
i
2
=
∇
∇⋅+
→
λρ
τ∂
∂
ρ
,
(19.7)
где
2
2
2
2
2
2
2
+
+
= ,
zyx z
k +
y
j +
x
i =
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∇∇
→→→
.
При
p
c
=const ,
уравнение
(19.7)
примет
вид
TaTw
T
2
= +
∇
∇⋅
→
∂τ
∂
, (19.8)
228
или
с
учетом
выражения
для
полной
производной
T w
TT
+
d
D
∇⋅=
→
τ∂
∂
τ
окончательно
получим
=
d
D
2
Ta
T
∇
τ
(19.9)
Уравнение
теплоотдачи
Из
граничных
условий
III-
го
рода
(
)
0=nw
)/( - = -
nTTT ∂∂
∞
λα
получим
уравнение
теплоотдачи
∞
−
∂
∂
TT
nT
)/(
- =
w
0=n
λ
α
. (19.10)
Краевые
условия
(
условия
однозначности
)
Чтобы
решить
конкретную
задачу
,
к
дифференциальным
уравнениям
сохранения
следует
присоединить
условия
однозначности
-
геометрические
(
характеризующие
форму
и
размеры
тела
),
физические
(
характеризующие
свойства
потока
),
начальные
и
граничные
(
распределение
полей
скорости
и
температуры
потока
на
входе
в
канал
,
условия
теплообмена
на
поверхности
тела
).
Часто
поставить
граничные
условия
можно
лишь
в
результате
решения
внешней
и
внутренней
задач
.
Например
,
при
обтекании
трубы
газом
,
внутри
которой
движется
поток
,
температуры
поверхностей
не
могут
быть
назначены
произвольно
,
а
определяются
из
уравнения
теплового
баланса
,
составленного
для
двух
сред
,
с
учетом
теплопроводности
стенки
.
Особенности
теплообмена
при
турбулентном
течении
Исследования
показывают
,
что
в
неподвижной
точке
турбулентного
потока
мгновенная
скорость
w
пульсирует
около
среднего
во
времени
значения
скорости
w
,
то
есть
www
′
+
=
,
где
w′
-
пульсационная
скорость
;
( )
∫
∆+
∆
ττ
τ
ττ
τ
dww
1
= ;
∆
τ
-
промежуток
времени
,
который
значительно
больше
чем
время
периода
п
τ
.
Аналогичное
выражение
можно
написать
для
температуры
T
=
T
T
′
+
,
∫
∆+
∆
=
ττ
τ
ττ
τ
dTT
)(
1
.
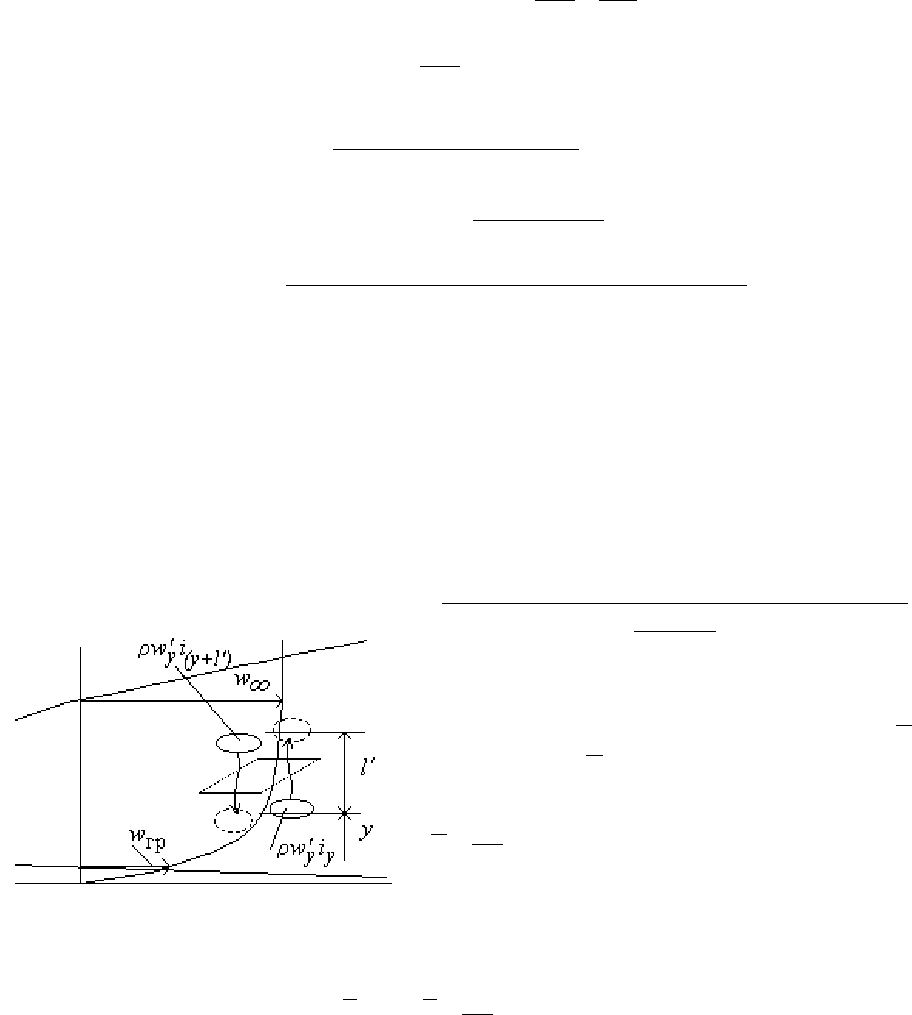
Рассмотрим
процесс
передачи
теплоты
в
турбулентном
пограничном
слое
.
Мысленно
выделим
в
нем
элементарную
площадку
,
параллельную
поверхности
обтекаемой
пластины
и
рассмотрим
потоки
энтальпии
через
нее
(
рис
.19.3).
На
координате
у
в
направлении
от
стенки
имеем
:
yy
i w
ρ
′
,
на
координате
ly
′
+
в
обратном
направлении
:
( )
ly+y
iw
′
′
ρ
,
где
l
′
-
длина
пути
смешения
(
такая
запись
предполагает
равенство
пульсационных
скоростей
и
плотности
на
соответствующих
координатах
).
Результирующий
поток
,
равный
разности
этих
потоков
,
определит
плотность
теплового
потока
Рис
.19.3

229
( )
(
)
( )
( )
=−
′
−=
=
′
′
′
+
′
lyyy
ly+yyy
iiw
iw-i w =-q
ρ
ρ
ρ
т
y
T
y
T
l w = - cl
y
i
w
ypy
∂
∂
λ
∂
∂
ρ
∂
∂
ρ
_
т
__
- −=
′′′′
=
, (19.11)
где
pт
l w
с
y
′
′
=
ρ
λ
-
коэффициент
турбулентной
теплопроводности
,
который
зависит
не
только
от
теплофизических
свойств
жидкости
(
)
ρ
,
p
c
,
но
и
режимных
параметров
потока
(
)
l w
y
′
′
,
.
В
общем
случае
( )
y
T
q
∂
∂
λλ
_
т
+−=
.
Так
как
пульсационная
составляющая
скорости
y
w
l w
x
y
∂
∂
′
≈
′
,
то
вместо
(19.11)
можно
записать
′
−=
y
T
y
w
lq
x
∂
∂
∂
∂
ρ
__
2
pт
c , (19.11а)
где = kyl
′
; k
≈
0,4.
20. Подобие и моделирование процессов конвективного теплообмена
Критерии подобия и критериальные уравнения
Рассмотрим теплоотдачу около вертикальной стенки.
Запишем уравнение сплошности
0
=+
y
w
x
w
y
x
∂
∂
∂
∂
(а)
в безразмерном виде, введя безразмерные величины путем деления на соответствующие
масштабы (l - масштаб длины, w
∞
- масштаб скорости):
∞∞
==
w
w
w
w
w
w
l
y
=y
l
x
=x
y
y
x
x
,, , .
Тогда
∞∞
⋅⋅== ww = w ww = wlyylxx
y
y
x
x
____
,,,
и подстановка в (а) дает
0 =
∞
y
w
+
x
w
l
w
y
x
∂
∂
∂
∂
, или
0 =
y
w
+
x
w
y
x
∂
∂
∂
∂
. (20.1)
Из (20.1) видно, что приведение уравнения сплошности к безразмерной форме не
изменило его. Обезразмерим уравнение движения для стационарного режима
β
+
+
1
=
2
2
2
2
ϑ
∂
∂
∂
∂
ν
∂
∂
ρ∂
∂
∂
∂
g
y
w
x
w
x
p
y
w
+ w
x
w
w
xxx
y
x
x
+
−
,
(20.2)
вводя безразмерные переменные
∞
−
TT =
ww
ϑ
,
=
ww
∞
∞
−
−
=
TT
TT
ϑ
ϑ
θ
,
∞
p
p
=p :
. g
w
θβϑ
∂
∂
∂
∂
ν
∂
∂
ρ∂
∂
∂
∂
+
++⋅−=
+
∞∞∞
2
x
2
2
x
2
2
x
y
x
x
2
y
w
x
w
l
w
x
p
l
p
y
w
w
x
w
w
l
w
Разделим все члены уравнения на комплекс
2
l
w
∞
ν
, тогда:
230
∞∞
∞∞
+++⋅−=
+
w
lg
y
w
x
w
x
p
w
lp
y
w
w
x
w
w
lw
2
w
2
x
2
2
x
2
x
y
x
x
ν
θϑ
∂
∂
∂
∂
∂
∂
νρ∂
∂
∂
∂
ν
β
,
EuRe
=⋅=⋅
∞
∞
∞
∞
∞
∞
∞
νρνρ
lw
w
p
w
w
w
lp
2
,
Re
Gr1
gg
2
3
w
2
w
=⋅=⋅⋅
∞
∞
ν
ν
βϑ
ν
ν
ν
βϑ
lw
l
l
l
w
l
.
θ
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
⋅+++−=
+
Re
Gr
EuReRe
2
x
2
2
x
2
x
y
x
x
y
w
x
w
x
p
y
w
w
x
w
w
(20.3)
Уравнение движения в безразмерном виде содержит три безразмерных критерия подобия:
ν
lw
∞
= Re - критерий Рейнольдса - характеризует соотношение между силами инерции и
силами вязкости,
2
=Eu
∞
∞
w
p
ρ
- критерий Эйлера - соотношение между силами статического давления и
удвоенным динамическим напором
∆
=
∞
2
Eu
виде
в
сязаписывает
он
часто
w
p
ρ
.
2
3
w
=Gr
ν
ϑβ
lg
- критерий Грасгофа - характеризует соотношение между подъемными
силами и силами вязкости.
Обезразмерим уравнение энергии. Для стационарного режима можно написать:
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
2
2
2
2
y
T
x
T
a
y
T
w
x
T
w
yx
.
Вводя обозначения
∞∞
−=−=
TTTT
ww
ϑϑ
, ,
∞
=
w
w
w
x
x
, ,
∞
=
w
w
w
y
y
w
ϑ
ϑ
θ
=
, получим
безразмерную форму
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
∞
2
2
2
2
2
yxl
a
y
w
x
w
l
w
w
yx
w
θθ
ϑ
θθ
ϑ
.
Разделим обе части на комплекс
2
l
a
w
ϑ
:
2
2
2
2
yxy
w
x
w
a
lw
yx
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
∞
θθθθ
.
Введем критерий Пекле
a
lw
∞
=
Pe
l
CwlCw
pp
ϑ
λ
ρϑ
ϑ
ϑ
λ
ρ
∞∞
=⋅=
,
где выражение в числителе характеризует конвективный теплоперенос, а в знаменателе –
перенос теплопроводностью.
2
2
2
2
Pe
yxy
w
x
w
yx
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
θθθθ
. (20.4)
Число Пекле можно записать в виде произведения двух других безразмерных критериев и
тем самым исключить из числа переменных задачи:

231
PrRePe
⋅=⋅=⋅=
a
wl
a
wl
ν
νν
ν
,
где
λ
µ
ρλ
ρ
µ
ν
pp
CC
a
===Pr
- критерий Прандтля, характеризующий соотношение между
теплотой, выделившейся в результате трения, и теплотой, переданной за счет
теплопроводности.
Обезразмерим уравнение теплоотдачи.
∞
=
−
∂
∂
−=
TT
y
T
w
y 0
λ
α
,
w
y
y
ϑ
ϑ
λ
α
0=
∂
∂
−=
,
l
y
w
y
w
ϑ
θ
λϑ
α
0=
∂
∂
−=
,
Nu
0
=
∂
∂
−=
=y
y
l
θ
λ
α
. (20.5)
Здесь Nu - критерий Нуссельта (безразмерный коэффициент теплоотдачи).
Таким образом,
yx
wwyx ,,NuEu,,,Gr,PePr,Re,,,
θ
могут считаться новыми
переменными, которые можно разделить на независимые yx, и зависимые
yx
ww ,,
θ
переменные и постоянные для данной задачи при постоянных физических условиях
величины:
Eu Nu.Gr,Pe,Pr,Re,,
Последние
,
в
свою
очередь
,
разделяются
на
определяемые
критерии
EuNu,
и
определяющие
Re, Pr, Pe, Gr.
Полученные
безразмерные
уравнения
теплоотдачи
,
движения
и
энергии
содержат
меньше
переменных
,
чем
исходные
размерные
,
что
облегчает
их
анализ
и
решение
,
а
также
обобщение
результатов
расчетов
или
экспериментов
.
Уравнения
,
записанные
через
новые
переменные
,
называются
критериальными
уравнениями
:
(
)
GrPr,Re,,,Nu
cc
yx
ϕ
= , (20.6)
(
)
GrPr,Re,,,
yxw
x
ψ
= , (20.7)
(
)
GrPr,Re,,, yxf=
θ
. (20.8)
Критериальные
уравнения
являются
основой
для
обработки
опытных
данных
в
безразмерном
виде
.
Уравнения
сохранения
для
пограничного
слоя
Применим
полученные
уравнения
сохранения
к
пограничному
слою
.
Для
этого
сделаем
оценку
величины
слагаемых
,
входящих
в
уравнения
сплошности
0=
∂
∂
+
∂
∂
y
w
x
w
y
x
и
движения
.Re
2
2
2
2
y
w
x
w
y
w
w
x
w
w
xxx
y
x
x
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
Так
как
в
уравнении
сплошности
xиw
x
имеют
порядок
равный
единице
(
они
изменяются
от
нуля
до
единицы
),
а
−
y порядок
δ
=δ/l
0
,
то
и
y
w
имеет
порядок
δ
.
Исходя
из
этого
в
уравнении
движения
2
2
2
2
y
w
x
w
xx
∂
∂
<<
∂
∂
,
и
оно
для
пластины
принимает
вид
:
2
2
Re
y
w
y
w
w
x
w
w
xx
y
x
x
∂
∂
=
∂
∂
+
∂
∂
(20.9).
