Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.

192
х
=0, а
α
=
∞
:
λ
δ
δ
2
2
0
v
x
q
tt
=−
=
(16.27)
Теплопроводность цилиндрического стержня
при наличии внутренних источников теплоты
Так как 0=
∂
∂
=
∂
∂
z
TT
ϕ
, то дифференциальное уравнение теплопроводности
примет вид: 0
1
=+
ρ
ϑ
c
q
dr
d
r
dr
d
r
a
v
λ
ϑ
v
q
dr
d
r
dr
d
r
−=
1
, где
ϑ
=T
(
r
)-
T
ж
.
Разделив переменные и проинтегрировав два раза,
получим закон изменения температуры в стенке:
rdr
q
dr
d
rd
v
λ
ϑ
−=
,
1
2
2
C
rq
dr
d
r
v
+−=
λ
ϑ
,
r
C
rq
dr
d
v
1
2
+−=
λ
ϑ
, (а)
21
2
ln
4
CrC
rq
v
++−=
λ
ϑ
. (в)
При
r
=0:
0
0
=
=
r
dr
d
ϑ
– в силу симметричности за-
дачи C
1
=0.
При
r=r
0
:
0
0
rr
rr
dr
d
=
=
=
−
αϑ
ϑ
λ
.
Так как
λ
ϑ
2
0
0
rq
dr
d
v
rr
−=
=
, а
2
2
0
0
4
C
rq
v
rr
+−=
=
λ
ϑ
, то
+−=
2
2
00
42
C
rqrq
vv
λ
α
,
λα
4
2
2
00
2
rqrq
С
vv
+=
⇒
.
(с)
Подставляя (с) в (в), получим:
αλλ
ϑ
2
4
4
0
2
0
2
rqrqrq
vvv
++−= , или
αλ
ϑ
2
1
4
0
2
0
2
0
rq
r
r
rq
vv
+
−=
. (16.28)
Найдем плотность теплового потока:
−−=−=
λ
λ
ϑ
λ
2
rq
dr
d
q
v
=
2
rq
v
. (16.29)
На поверхности стержня будем иметь
2
0
0
rq
q
v
rr
=
=
. (16.30)
Вернемся к формуле (16.28):
αλ
ϑ
2
1
4
0
2
0
2
0
rq
r
r
rq
vv
+
−=
.
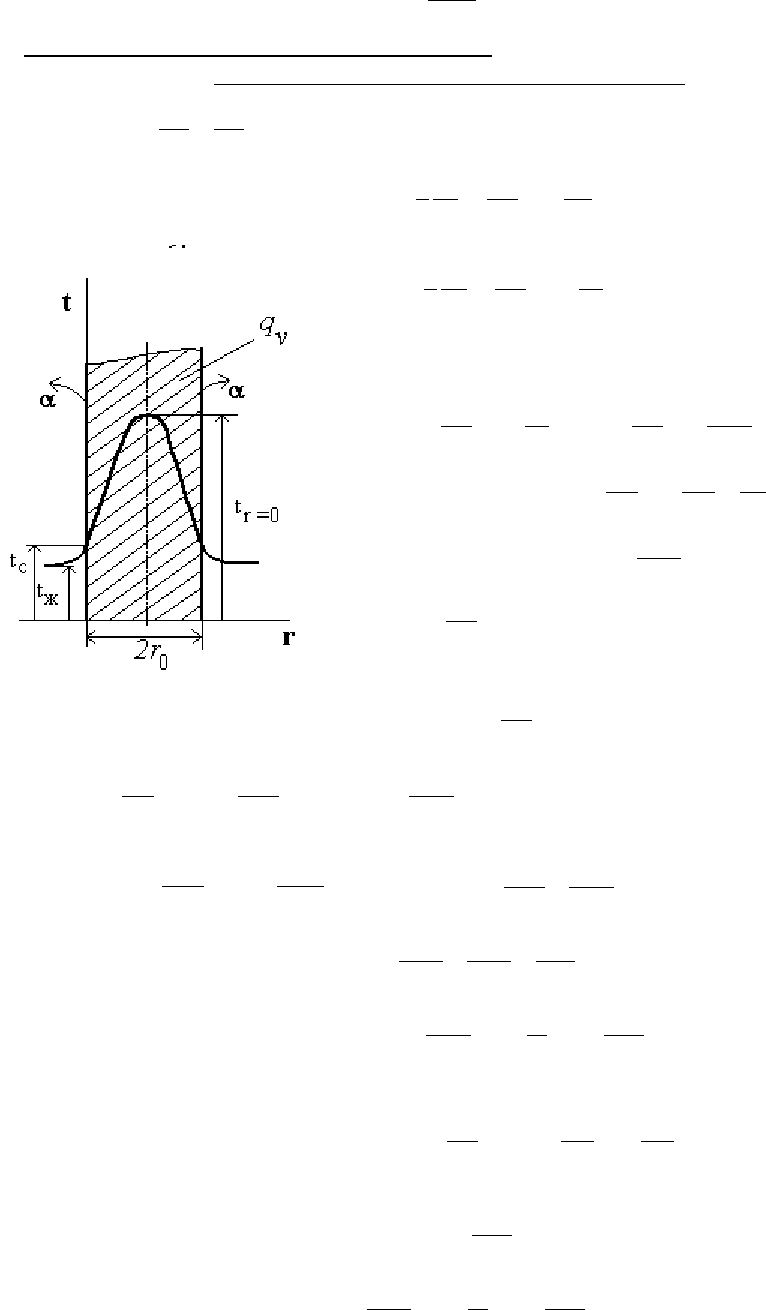
Рис.16.9
193
При
r=r
0
:
ж
0
2
0
tt
rq
c
v
rr
−==
=
α
ϑ
, тогда
α
2
0
ж
rq
tt
v
c
+= . Из полученного выраже-
ния видно, что ухудшение теплоотдачи может привести к значительному росту
температуры стенки.
Полагая в (16.28)
r=r
0
и α=∞, получим разность температур между центром и
пверхностью стержня
λ
4
2
0
0
0
rq
tt
v
r
=−
. (16.31)
В самом общем случае
q
v
является функцией времени и координат.
Теплопроводность цилиндрической стенки при наличии
внутренних источников теплоты
Данная задача разбивается на три задачи:
1.
Внутренняя стенка теплоизолирована.
2.
Наружная стенка теплоизолирована.
3.
Имеет место теплоотдача от внутренней и наружной поверхности.
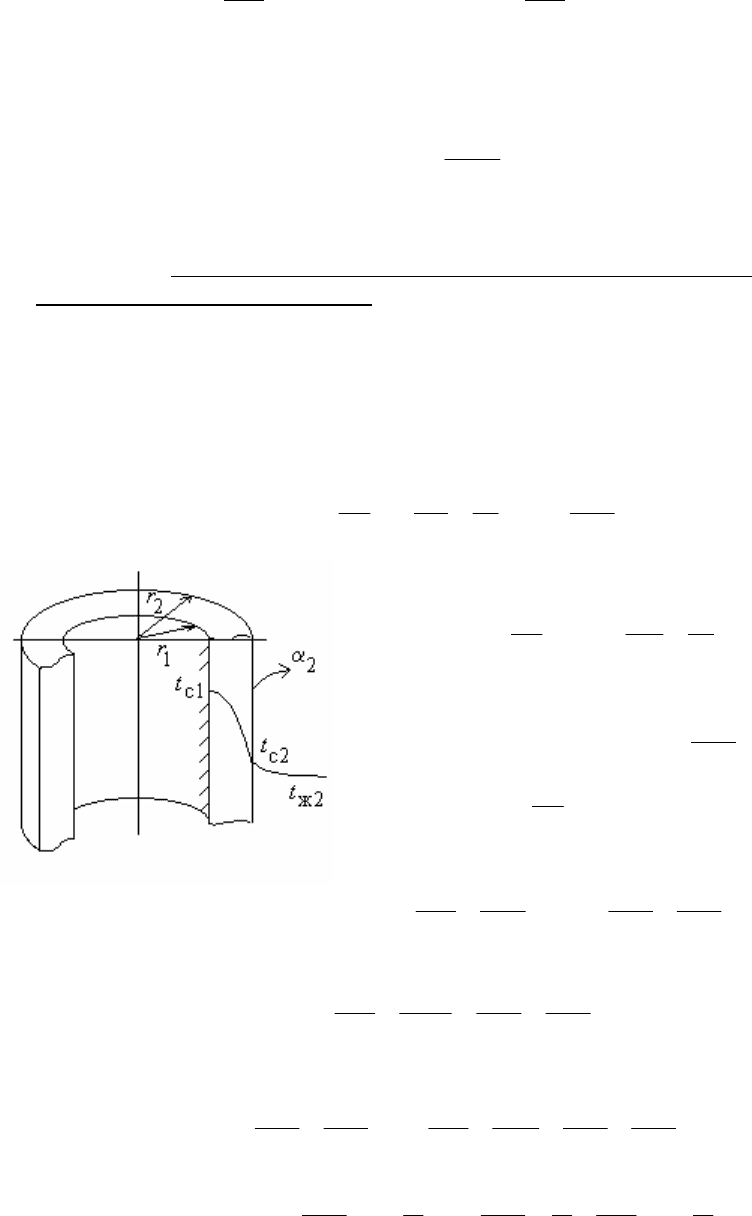
1.Теплота отводится через наружную поверхность (рис.16.10).
Применим полученное выше решение
r
C
rq
dr
d
v
1
2
+−=
λ
ϑ
,
21
2
ln
4
CrC
rq
v
++−=
λ
ϑ
(*)
с новыми граничными условиями для рассматри-
ваемого случая.
При
r
=
r
1
: 0
2
1
1
1
1
=+−=
=
r
C
rq
dr
d
v
rr
λ
ϑ
-внутренняя
стенка теплоизолирована
λ
2
2
1
1
rq
С
v
=
. (а)
При
r=r
2
:
2
2
rr
rr
dr
d
=
=
=
−
αϑ
ϑ
λ
,
++−=
+−−
22
2
1
2
2
2
2
12
ln
2422
Cr
rqrq
r
rqrq
vvvv
λλ
α
λλ
λ
От-
сюда находим
С
2
:
2
2
1
2
2
2
2
12
2
ln
2422
r
rqrq
r
rqrq
C
vvvv
λλαα
−+−= .
Подставим
С
1
и
С
2
в (*):
2
2
1
2
2
2
2
12
2
1
2
ln
2422
ln
24
r
rqrq
r
rqrq
r
rqrq
vvvvvv
λλααλλ
ϑ
−+−++−=
;
−++
−=
2
2
1
2
2
2
1
2
2
2
2
1
2
ln
2
1
4 r
r
rq
r
r
rq
r
r
rq
vvv
αλλ
ϑ
. (16.32)
Плотность теплового потока найдем по формуле
Рис.16.10
194
−=−=
+−−=−=
2
1
2
11
1
2222 r
rrq
r
rqrq
r
Crq
dr
d
q
vvvv
λ
λ
ϑ
λ
. (16.33)
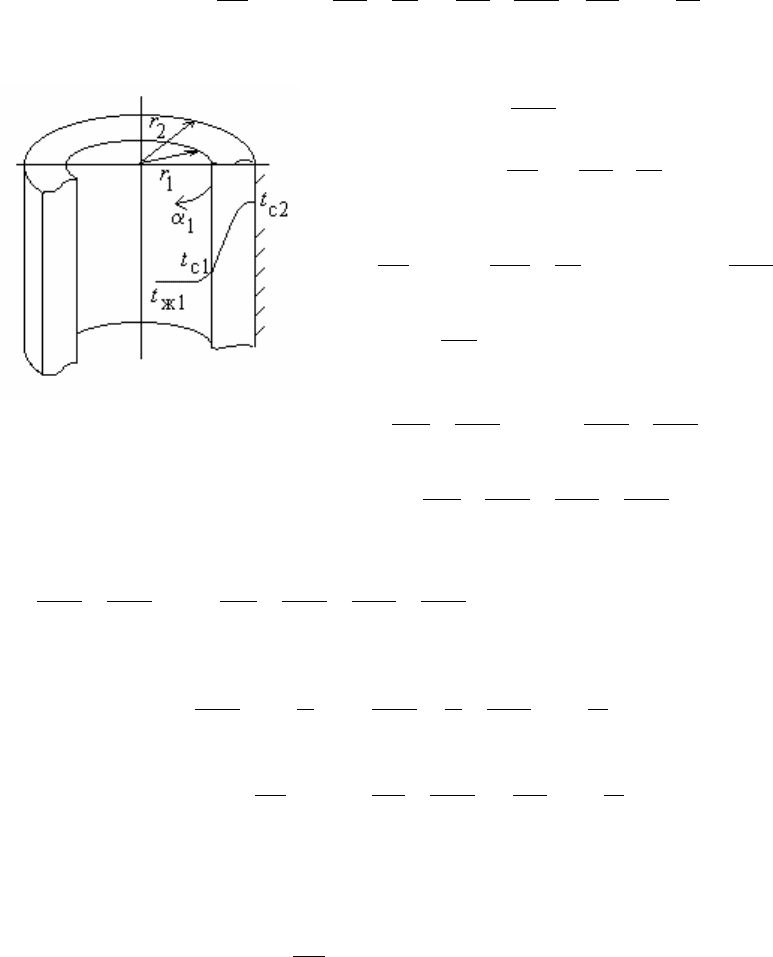
2.Теплота отводится через внутреннюю поверхность (рис.16.11).
21
2
ln
4
CrC
rq
v
++−=
λ
ϑ
, (а)
r
C
rq
dr
d
v
1
2
+−=
λ
ϑ
. (b)
Граничные условия:
r=r
2
, 0=
dr
d
ϑ
, ,
2
0
2
2
2
1
2
1
2
λλ
rq
C
r
C
rq
vv
=
⇒
=+−
r=r
1
,
1
1
rr
rr
dr
d
=
=
=
−
αϑ
ϑ
λ
,
.ln
2422
,ln
2422
1
2
2
2
1
1
2
21
2
21
2
2
2
1
1
2
21
r
rqrq
r
rqrq
C
Cr
rqrq
r
rqrq
vvvv
vvvv
λλαα
λλ
α
λλ
λ
−+−=⇒
++−=
+−−
Подставляя
С
1
и
С
2
в (а), получим:
1
2
2
2
1
1
2
21
2
2
2
ln
2422
ln
24
r
rqrq
r
rqrq
r
rq
rq
vvvvv
v
λλααλλ
ϑ
−+−++−= , откуда, группируя слагаемые,
найдем:
−++
−=
2
1
21
1
2
2
2
1
2
1
1
2
ln
2
1
4 r
rrq
r
r
rq
r
r
rq
vvv
αλλ
ϑ
,
−=
+−−=−=
2
2
2
2
1
222
r
r
rq
r
rqrq
dr
d
q
vvv
λλ
λ
ϑ
λ
. (16.34)
3. Теплота отводится через внутреннюю и наружную поверхности
Очевидно, что в случае отвода теплоты с обеих поверхностей трубы, кри-
вая распределения температуры должна иметь максимум при некотором значении
радиуса
r
0
, следовательно,
0
0
=
r
dr
d
ϑ
. Таким образом, поверхность при
r= r
0
можно считать теплоизолированной и разбить задачу на две уже рассмотренные -
в области
r
1
≤
r
≤
r
0
- с теплоизолированной внешней стенкой и в области
r
0
≤
r
≤
r
2
- с теплоизолированной внутренней стенкой. Задача сводится к определению
неизвестного
r
0
.
Решая задачу с теплоизолированной внешней поверхностью, находят рас-
пределение температуры между
r
1
и
r
0
. После этого рассматривают задачу с теп-
лоизолированной внутренней поверхностью для области
r
0
≤
r
≤
r
2
. Приравнивая
значения температуры при
r= r
0
, находят радиус
r
0
.
Рис. 16.11

195
Теплопроводность тонкого стержня
В технике часто встречаются случаи, когда коэффициенты теплоотдачи по
разные стороны стенки, разделяющей жидкости или газы, значительно отличают-
ся друг от друга.
Для плоской стенки можно написать
(
)
2ж1ж
ttkq −=
, Вт/м
2
, где
21
11
1
αλ
δ
α
++
=
k
;
qFQ
=
&
, Вт ;
τ
qFQ
=
, Дж.
При 0≈
λ
δ
и
12
αα
<<
2
21
21
α
αα
α
α
≈
+
=
k
.
Таким образом, коэффициент теплопередачи приблизительно равен наи-
меньшему коэффициенту теплоотдачи. При заданном тепловом потоке
Q
&
это
приводит к большим значениям поверхности
F
. Применение оребрения позволяет
уменьшить термическое сопротивление со стороны наименьшего коэффициента
теплоотдачи и тем увеличить коэффициент теплопередачи
k
.
Чтобы решать задачи, связанные с отводом или подводом теплоты через
ребристые поверхности, необходимо знать закон распределения температуры в
тонком стержне, так как ребра, как прави
ло, можно считать тонкими стержнями.
Задача стационарная и одномерная , следовательно:
0=
τ∂
∂
T
; 0==
z
Т
y
T
∂
∂
∂
∂
.
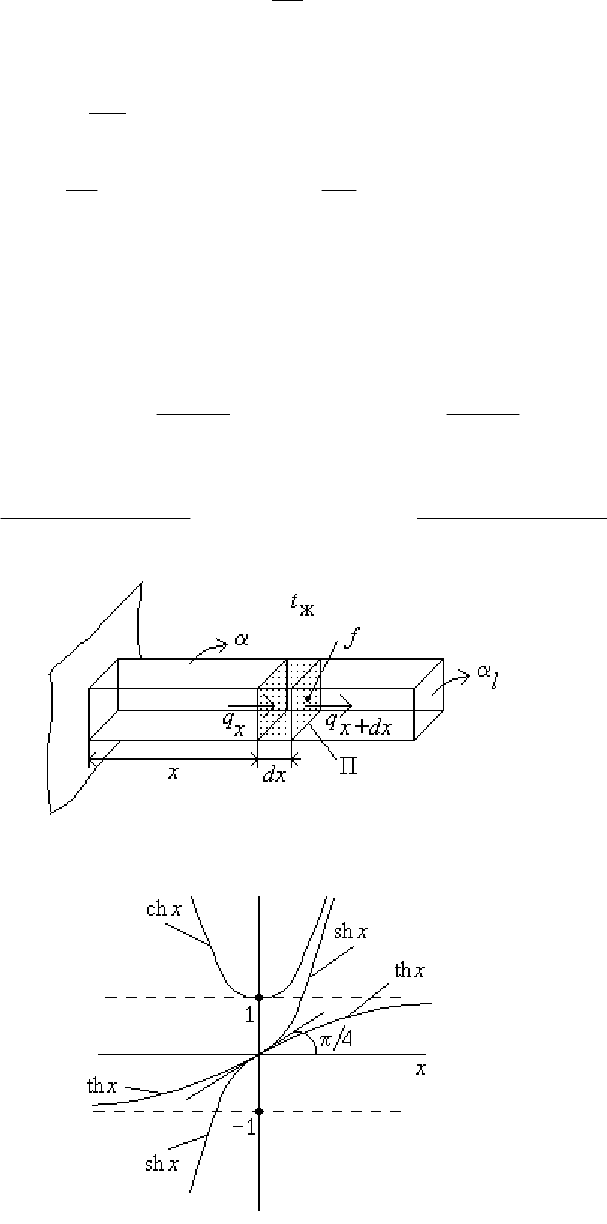
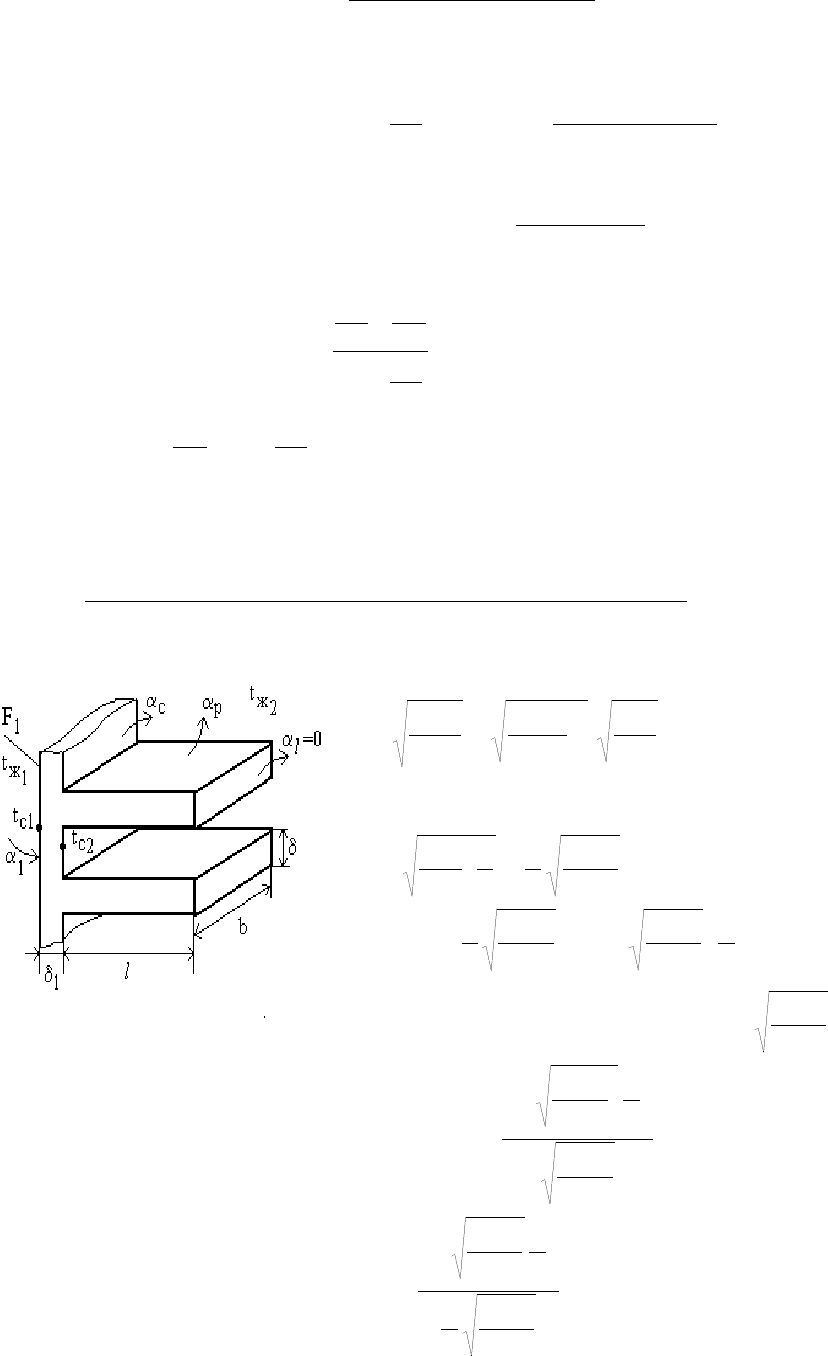
Выделим в стержне с постоянным поперечным сечением
f
элементарный объем
dV=f dx
(рис.16.12) и рассмотрим для него баланс тепловых потоков
( )
dxfqfq
dxxx
Π=−
+
αϑ
, (а)
где
( )
fqfq
dxxx
+
, - соответственно входящий и выходящий тепловые потоки;
dx
Π
αϑ
- тепловой поток, отдаваемый окружающей среде с элементарной боковой
поверхности
dx
Π
, но
( )
....+ ++
dx
dx
dq
dq=q=qq
xxx+dx
. (b)
Подставляя (b) в (а), имеем:
dxdx=f
dx
dq
ϑ
Π−
α
.
(с)
Так как
dx
d
q
ϑ
λ
−= , то
2
2
dx
d
dx
dq
ϑ
λ
−= . (d)
Подставляя (d) в (с), получаем дифференциальное уравнение теплопроводности
для стержня:
ϑ
αϑ
fdx
d
λ
2
2
Π
=
, (16.35)
где
(
)
ж
txt −=
ϑ
;
const
ж
=t
.
Частное решение этого уравнения имеет вид:
mx
Сe
=
ϑ
. (е)
Подставим (е) в (16.35)
⇒
mxmx
Сe
f
eСm
λ
2
Π
=
α
, тогда
f
m
λ
Π
±=
α
.
Теперь общее решение:
-mxmx
eСeС
21
+=
ϑ
. (16.36)
196
Найдем
С
1
и
С
2
из граничных условий.
При
210
0= CCx +=
ϑ
,
102
CC
−=
ϑ
;
при
lxl
l
dx
d
l x
=
=
ϑα
ϑ
=x
λ
- =
. (*)
Подставим значение
C
2
в (16.36) :
mxmxmx
eCeeC
−−
−+=
101
ϑϑ
,
откуда
-ml-mlml
l
meCmemeC
dx
d
101
=x
+−=
ϑ
ϑ
.
Подставим
lx
=
ϑ
и
lx
dx
d
=
ϑ
в (*) и введем
λ
α
m
n
l
= , тогда:
(
)
(
)
-ml-mlml
l
ml-mlml
eCeeCmeCmemeC
101101
−+=+−−
−
ϑαϑλ
,
-ml-ml
0
ml-ml-mlml
neCenneCeCeeC
11101
−+=−+−
ϑϑ
,
(
)
-mlml-mlml-ml
0
neCneCeCeCen
1111
1 −++=−
ϑ
,
(
)
(
)
(
)
-mlml-mlml-ml
eenCeeCen
−++=−
110
1
ϑ
.
Так как
2
)h(c
-xx
ee
x
+
= , а
2
)sh(
-xx
ee
x
−
= (рис.16.13), то
(
)
(
)
(
)
mlnCmlCen
-ml
sh2ch21
110
+=−
ϑ
, откуда
(
)
( ) ( )( )
mlmln
en
C
-ml
chsh2
1
0
1
+
−
=
ϑ
,
(
)
( ) ( )( )
mlmln
en
С
C
ml
chsh2
+1
0
102
+
=−=
ϑ
ϑ
.
Рис. 16.12
Рис. 16.13
Подставляя
C
1
и
C
2
в (16.36), найдем закон изменения температуры в стержне:
197
(
)
(
)
(
)
(
)
( ) ( )( )
mlmln
enen
l-xml-x-m
chsh2
+1-1
0
+
+
=
ϑϑ
. (16.37)
Определим поток теплоты, отдаваемый ребром окружающей среде (он равен по-
току теплоты, проходящему через основание стержня при
х
=0 ) :
(
)
(
)
( ) ( )
mlmln
mlmln
fm
dx
d
f
chsh
shch
Q
0
0=x
p
+
+
=
−=
ϑλ
ϑ
λ
&
. (16.38)
Вернемся к (16.37). Если пренебречь теплотой, отдаваемой торцом стержня
(
α
l
=0,
n=
0 ), то
(
)
(
)
( )
ml
ee
l-xml-x-m
ch2
00=n
+
=
ϑϑ
. (16.39)
Предположим, что стержень бесконечно длинный, тогда :
-mx
ml
ml
mx
ml
ml
mx
ln
e
e
e
e
e
e
e
0= 0,=
1
ϑϑ
=
+
+
=
∞
(16.40)
(в формуле 16.40 0→
ml
mx
e
e
, 0
1
→
ml
e
), следовательно,
(
)
-mx
ln
exp
0= 0,=
ϑϑ
=
∞
.
Вернемся к (16.38). Случай, когда торец стержня теплоизолирован:
(
)
ml f mQ
th
00=n p
ϑλ
=
&
. (16.41)
Плоская ребристая стенка с ребрами постоянного сечения
Преобразуем (16.41) с учетом геометрических размеров ребра
δ
⋅
f=b
,
(
)
δ
+=Π b2
=
Π
f
m=
р
λ
α
=
b
2b
р
λδ
α
λδ
α
р
2
(при
δ
>>
b -
тонкие ребра,
2b
≈
Π
). Умножим и разделим
подкоренное выражение на
δ
:
δ
δ
λδ
α
⋅
р
m
2
=
λ
δα
δ
р
2
1
= , тогда
λ
δα
δ
δλ
р
bQ
2
1
p
=
&
⋅⋅
δλ
δα
ϑ
l
р
2
th
0
Умножим и разделим на
λ
δα
р
2
:
λ
δα
δλ
δα
ϑδα
р
р
р
l
b
2
2
th
2Q
0р
⋅
=
&
.
Умножим
и
разделим
на
l:
,
2
2
th
2
0p
λ
δα
δ
δλ
δα
ϑα
р
р
р
l
l
lbQ
=
&
Рис
. 16.14
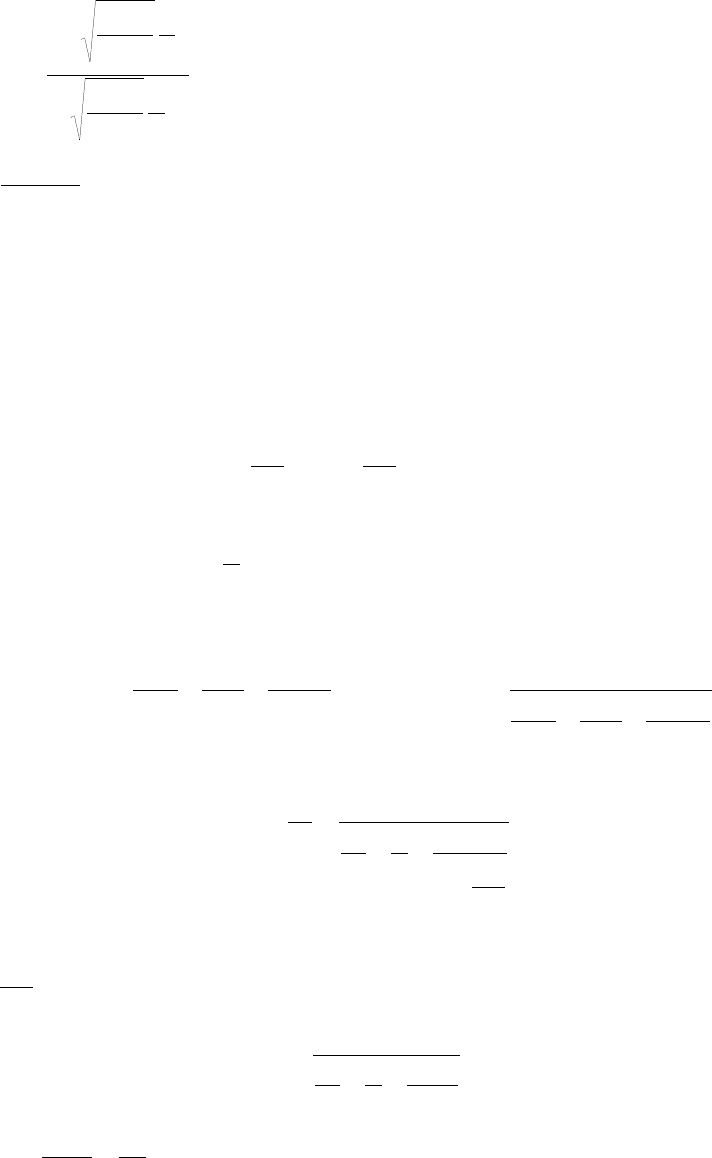
198
где
blF
p
2= -
поверхность
ребра
; EFQ
p 0pp
ϑα
=
&
,
(16.42)
где
δλ
δα
δλ
δα
l
l
E
р
р
2
2
th
=
-
коэффициент
эффективности
ребра
.
Из
(16.42)
следует
0p
p
=
ϑα
F
Q
E
р
&
,
т
.
е
.
Е
характеризует
отношение
теплового
потока
,
отдаваемого
окружающей
среде
ребром
(
p
Q
&
),
к
тепловому
потоку
,
который
отдает
идеальное
ребро
с
нулевым
термическим
сопротивлением
(
)
0p
ϑα
F
р
.
Обозначим
: F
рс
-
пло
-
щадь
поверхности
ребристой
стенки
, zF
р
-
общая
площадь
поверхности
ребер
, F
с
-
площадь
неоребренной
поверхности
(
между
ребер
).
Введем
понятие
приведенного
коэффициента
теплоотдачи
EzFFFQ
oc 0ppc0pcпр
ϑαϑαϑα
+==
&
,
где
z -
число
ребер
.
pc
p
p
pc
c
спр
F
F
zE
F
F
ααα
+= ;
pcpc
+ zFFF = .
Составим
уравнение
теплового
баланса
для
ребристой
стенки
(
)
c1
ж
111
= ttFQ −
α
&
,
( )
1c2c1
= FttQ −
δ
λ
&
,
(
)
ж
2c2pc
пр
= ttFQ −
α
&
.
Разрешая
уравнения
относительно
разностей
температур
и
складывая
их
с
учетом
Q=const,
можно
написать
ж
2
ж
1
pc
пр
111
-
11
tt
FFF
Q =
++
αλ
δ
α
&
;
pcпр111
ж2ж1
11
-
=
FFF
tt
Q
αλ
δ
α
++
&
. (16.43)
Найдем
плотность
теплового
потока
,
отнесенную
к
неоребренной
поверхности
:
1
pc
пр
1
ж2ж1
1
1
11
-
=
F
F
tt
F
Q
q
α
λ
δ
α
++
=
&
.
Введем
понятие
коэффициента
оребрения
:
1
1
pc
>=
F
F
β
,
с
учетом
чего
βαλ
δ
α
пр1
ж2ж1
1
11
-
=
++
tt
q . (16.44)
Так
как
,
11
спр
αβα
<
то
применение
ребристой
поверхности
позволяет
уменьшить
термическое
сопротивление
со
стороны
наименьшего
коэффициента
теплоотдачи
,
следовательно
,
для
заданного
потока
теплоты
Q
&
потребуется
меньшая
по
-
верхность
F
1.
199
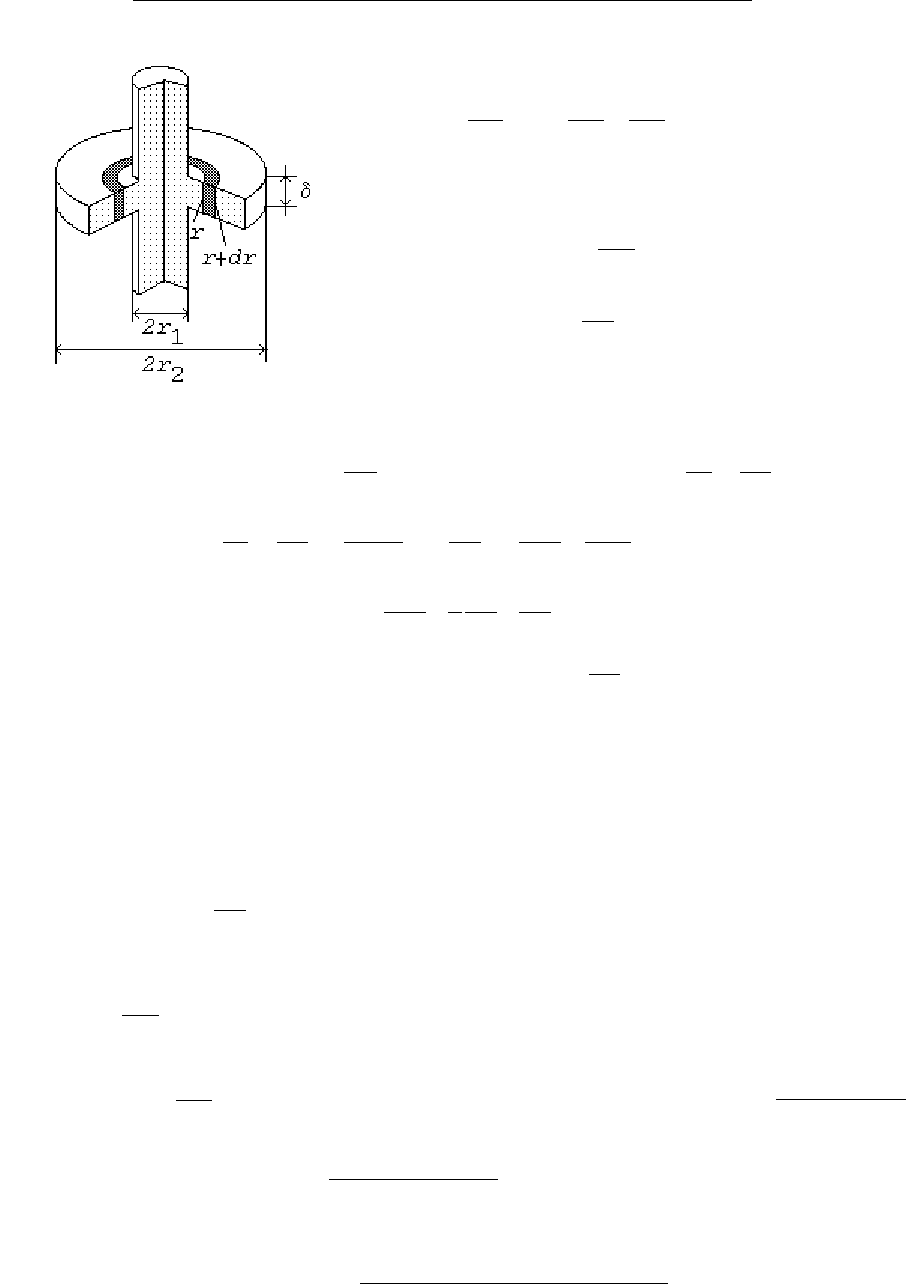
Передача
теплоты
через
круглое
ребро
постоянного
сечения
Повторяя
в
целом
подход
для
случая
тонкого
стержня
,
получим
дифференциальное
уравнение
теп
-
лопроводности
для
круглого
ребра
.
const=
ж
t
, 0=
τ∂
∂
T
, 0==
ϕ∂
∂
∂
∂
T
z
T
,
(
)
ж
-trt=
ϑ
.
Тепло
-
вые
потоки
на
радиусах
r
и
r+dr
соответственно
равны
r
Q
&
= -2
λπ
r
dr
d
ϑ
δ
, (a)
...++=
+
dr
dr
Qd
QQ
rdrr
&
&&
(b)
Вычитая
(b)
из
(a)
и
приравнивая
к
потоку
теплоты
,
отдаваемому
окружающей
среде
от
элемен
-
тарной
поверхности
ребра
22
⋅
rdr
π
,
получим
- 22 ⋅= rdrdr
dr
Qd
αϑπ
&
или
2
αϑπ
ϑ
λπδ
r
dr
d
r
dr
d
4=
,
λδ
αϑϑ
r
dr
d
r
dr
d 2
=
, 0
2
2
2
=−+
ϑ
λδ
αϑϑ
r
dr
d
r
dr
d
,
0
21
2
2
=−+
ϑ
λδ
αϑϑ
dr
d
r
dr
d
. (16.45)
Решение
уравнения
(16.45)
с
учетом
обозначения
2
2
m=
λδ
α
имеет
вид
(
)
(
)
mrKCmrIC
0201
+=
ϑ
, (16.46)
где
0
I
-
модифицированная
функция
Бесселя
I -
ого
рода
нулевого
порядка
;
0
K
-
модифицированная
функция
Бесселя
II -
ого
рода
нулевого
порядка
.
Граничные
условия
:
при
r=r
1
:
(
)
(
)
1021010
mrKCmrIC +=
ϑ
, (a)
при
r=r
2
:
2
2
rr
rr
dr
d
=
=
=
−
αϑ
ϑ
λ
.
Пренебрегая
тепловым
потоком
с
торцевой
поверхности
ребра
,
запишем
:
0
2
=
−
=rr
dr
d
ϑ
λ
,
тогда
,
взяв
производную
от
(16.46),
можно
написать
( ) ( )
0
212211
2
=−=
=
mrmKCmrmIC
dr
d
rr
ϑ
,
откуда
(
)
( )
21
212
1
mrI
mrKC
C =
.
Подставим
С
1
в
(
а
):
(
)
(
)
( )
( )
102
21
10212
0
mrKC
mrI
mrImrKC
+=
ϑ
и
найдем
вторую
констан
-
ту
интегрирования
:
(
)
(
)
(
)
(
)
(
)
2110210212210
mrImrKCmrImrKCmrI +=
ϑ
,
(
)
( ) ( ) ( ) ( )
.
21101021
210
2
mrImrKmrImrK
mrI
С
+
=
ϑ
Подставляя
С
2
в
выражение
для
С
1
,
получим
:
Рис
.16.15
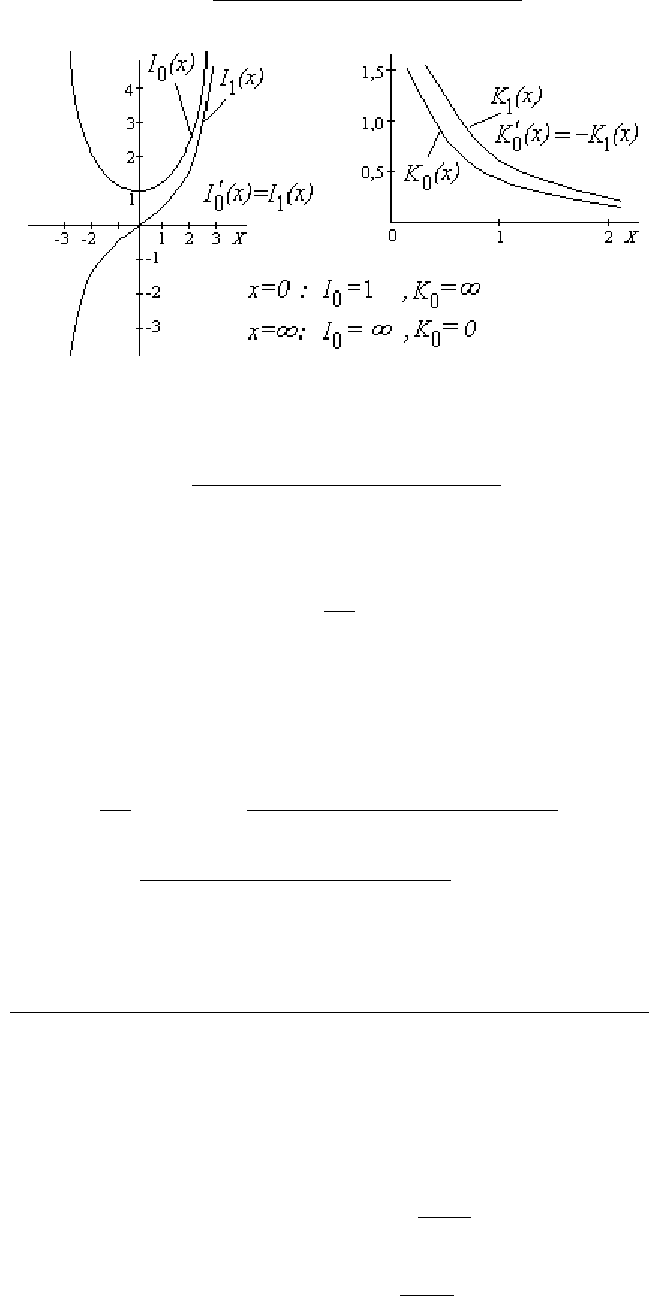
200
(
)
( ) ( ) ( ) ( )
21101021
210
1
mrImrKmrImrK
mrK
С
+
=
ϑ
.
Рис
. 16.16
С
учетом
констант
интегрирования
(16.46)
принимает
вид
:
(
)
(
)
(
)
(
)
( ) ( ) ( ) ( )
21101021
210021
0
mrImrKmrImrK
mrImrKmrImrK
+
+
=
ϑϑ
. (16.47)
Определим
тепловой
поток
,
который
отводит
круглое
ребро
постоянного
сечения
окружающей
среде
.
1
1
2
rr
p
dr
d
rQ
=
−=
ϑ
δλπ
&
.
(16.48)
Взяв
производную
от
(16.47) (
напомним
,
что
(
)
(
)
(
)
(
)
xKxKxIxI
1010
,
−
=
′
=
′
,
где
I
1
-
модифицированная
функция
Бесселя
первого
рода
первого
порядка
, K
1
-
модифицированная
функция
Бесселя
второго
рода
первого
порядка
)
(
)
(
)
(
)
(
)
( ) ( ) ( ) ( )
+
−
=
= 21101021
21111121
0
1
mrImrKmrImrK
mrImrKmrImrK
m
dr
d
rr
ϑ
ϑ
и
обозначая
(
)
(
)
(
)
(
)
( ) ( ) ( ) ( )
Ψ−=
+
−
21101021
21111121
mrImrKmrImrK
mrImrKmrImrK
,
окончательно
получим
Ψ= mrQ
p 01
2
ϑπλδ
&
,
Вт
(16.49)
Передача
теплоты
через
трапециевидные
и
треугольные
ребра
Ребра
такой
формы
более
эффективны
по
сравнению
с
ребрами
постоянной
тол
-
щины
.
Они
близки
по
свойствам
к
ребрам
с
q=const.
Составим
уравнение
теплово
-
го
баланса
для
элементарного
объема
,
выделенного
в
трапециевидном
ребре
(
см
.
рис
.16.18).
Разность
тепловых
потоков
на
координате
x
и
x+dx
при
стационарном
режиме
равна
потоку
,
отводимому
в
окружающую
среду
с
боковой
поверхности
элементарного
объема
.
ϕ
αϑ
cos
dx
QQ
xdxx
Π=−
+
&&
, (
а
)
где
(
)
ж
txt −=
ϑ
,
...++=
+
dx
dx
Qd
QQ
x
xdxx
&
&&
(b)
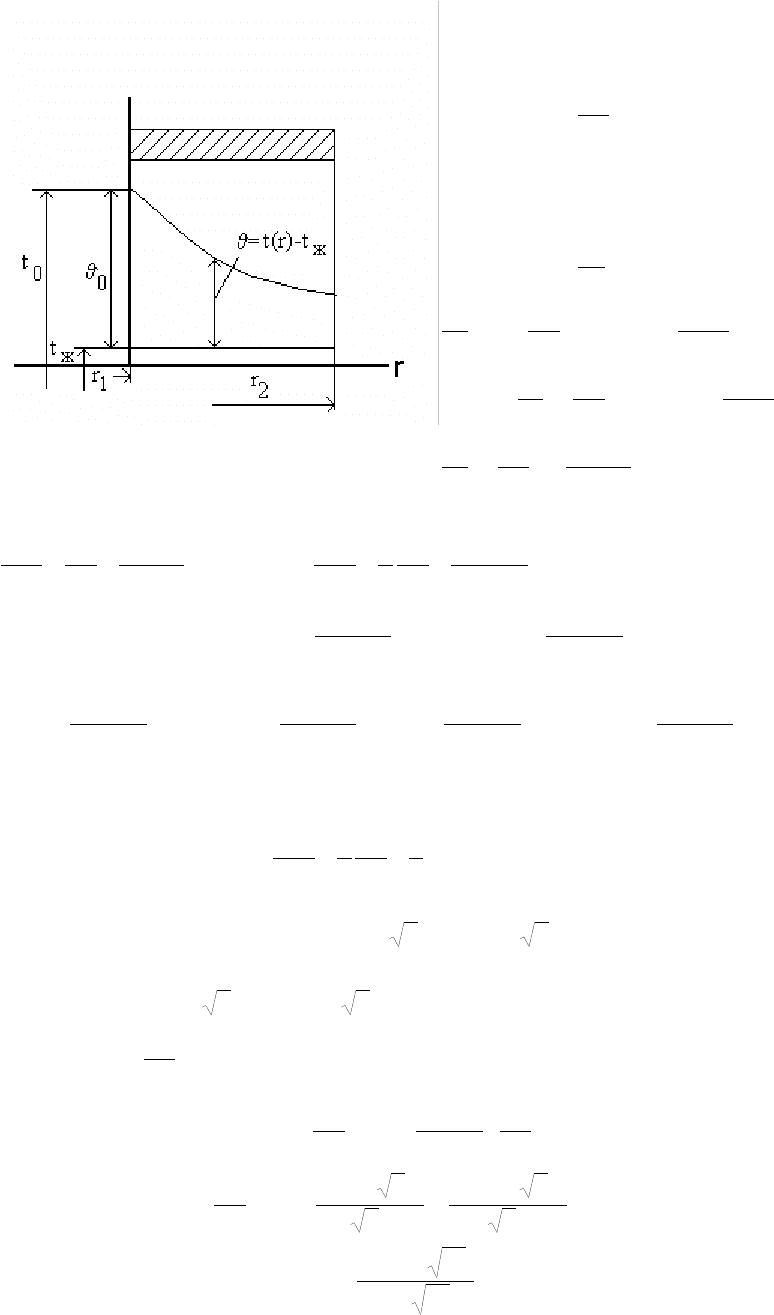
201
Так
как
тепловой
поток
на
-
правлен
противоположно
направле
-
нию
оси
x,
то
dx
d
bQ
x
ϑ
λδ
=
&
. (
с
)
С
учетом
геометрии
ребра
выполним
ряд
преобразований
:
(
)
bb 22 ≈+=Π
δ
,
ϕδ
δ
ϕ
tg2
2
tg x
x
=
⇒
= ,
ϕ
αϑ
ϑ
λδ
cos
2
dx
bdx
dx
d
b
dx
d
=
,
ϕ
αϑ
ϑ
ϕλ
cos
2tg2
dx
bdx
dx
d
x
dx
d
b =
,
ϑ
ϕλ
αϑ
sin
=
dx
d
x
dx
d
.
Теперь
уравне
-
ние
теплового
баланса
примет
вид
0
sin
2
2
=−+
ϑ
ϕλ
αϑϑ
dx
d
dx
d
x
,
или
0
sin
1
2
2
=−+
ϑ
ϕλ
αϑϑ
xdx
d
xdx
d
. (d)
Введем
новую
переменную
xz
ϕλ
α
sin
=
,
тогда
dxdz
ϕλ
α
sin
=
,
2
2
2
sin
dxdz
=
ϕλ
α
,
zx
α
ϕ
λ
sin
=
,
dzdx
α
ϕ
λ
sin
=
,
2
2
2
sin
dzdx
=
α
ϕλ
.
Подставляя
x, dx
и
dx
2
в
(d),
получим
модифицированное
дифференциальное
уравнение
Бесселя
для
трапециевидного
ребра
0
11
2
2
=−+
ϑ
ϑϑ
z
dz
d
z
dz
d
. (16.50)
Общее
решение
этого
уравнения
имеет
вид
:
(
)
(
)
zKCzIC 22
0201
+=
ϑ
. (16.51)
Граничные
условия
:
при
х=х
1
(
)
(
)
1
02
1
010
22 zKCzIC +=
ϑ
, (*)
при
х=х
2
0
2
2
==
−
=
=
xx
xx
dx
d
αϑ
ϑ
λ
(
здесь
мы
пренебрегаем
теплоотдачей
с
тор
-
цевой
поверхности
ребра
),
но
22
sin
zzxx
dz
d
dx
d
==
=
ϑ
ϕλ
αϑ
,
тогда
(
)
(
)
0
22
2
2
12
2
2
11
2
=−=
=
z
zKC
z
zIC
dz
d
zz
ϑ
,
(
)
( )
21
212
1
2
2
zI
zKC
C =
⇒ . (**)
Рис
. 16.17
