Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.

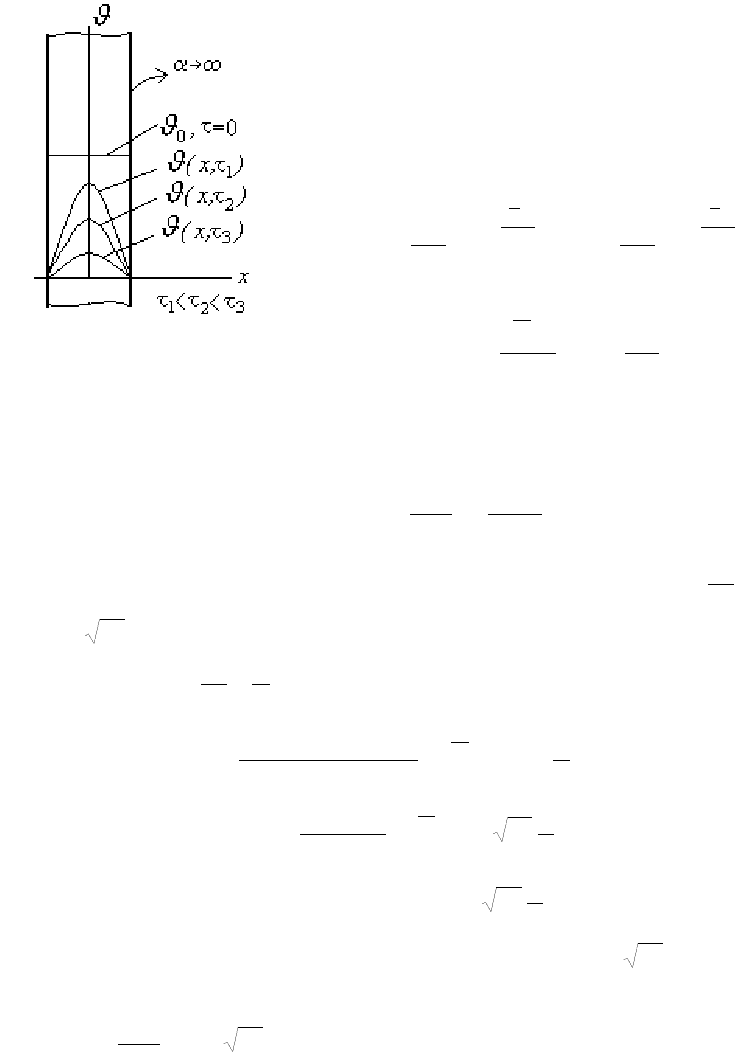
212
при x=
δ
0
=
θ
. При очень интенсивном теплообме-
не (
∞
→
α
) изменение температуры в теле не зави-
сит от внешних условий, а зависит от физических
свойств тела.
Преобразуем (17.5):
τ
δ
π
τ
δ
π
πθ
πθ
2
2
2
2
22
4
,
4
−
==
aa
ee ,
=
πθ
τ
δ
π
4
ln
2
2
2
a .
Эту формулу можно использовать, например,
для определения времени, необходимого для охла-
ждения или нагрева середины пластины до заданной температуры:
=
=
πθπ
δ
τ
0
2
2
4
ln
4
x
a
. (17.6)
2. Bi→0 (Bi<0,1), Fo>0,3 При Bi→0 решением уравнения
µ
µ
ctg=
Bi
бу-
дет Bi=
µ
(т.к. при
µ→
0 1cos ,sin
≈
≈
µ
µ
µ
,
тогда
1
Bi
µ
µ
= ), следовательно, из исходного уравнения
( )
+
=
−
δ
µ
µµµ
µ
ϑϑ
τ
δ
µ
x
e
a
1
111
1
0
cos
sincos
sin2
2
2
1
получим
( )
+
=
−
δµµ
µ
ϑϑ
τ
δ
x
Bie
Bi
a
cos
2
2
11
1
0
, или
=
−
δ
θ
x
Bie
BiFo
cos
. (17.7)
При х=0 ,
BiFo
x
e
−
=
=
0
θ
, (а) при х=
δ
,
(
)
Bie
BiFo
x
cos
−
=
=
δ
θ
.
(в)
Разделив (в) на (а), получим отношение температур на поверхности и в центре
пластины
(
)
1cos
0
≈=
=
=
Bi
x
x
θ
θ
δ
. Как видим, температура в теле практически посто-
янна, не зависит от физических свойств тела и определяется исключительно усло-
виями внешнего теплообмена.
Рис.17.3
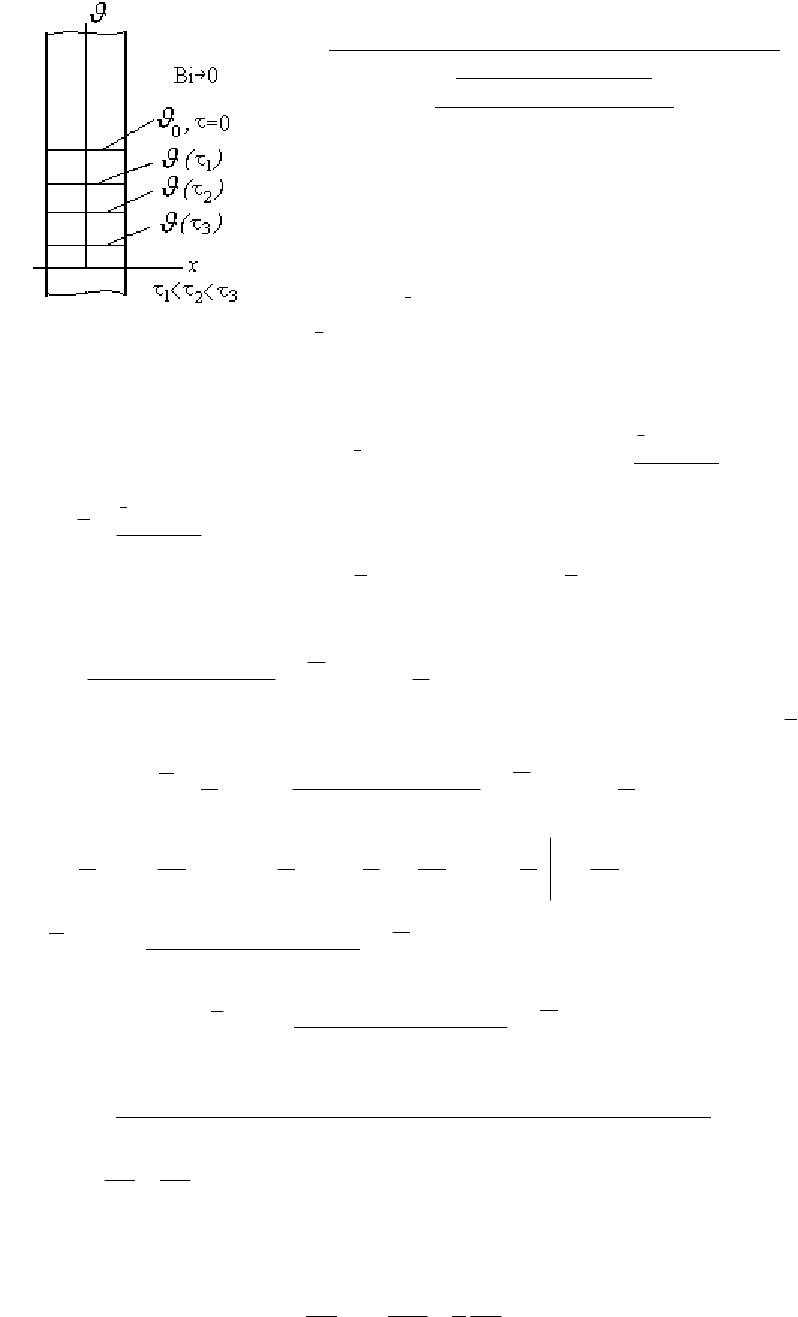
213
Количество теплоты отдаваемое пластиной
окружающей среде
в процессе охлаждения
Теплота, отданная пластиной, нагретой до темпе-
ратуры t
0
, при постоянной теплоемкости
С
, равна убы-
ли энтальпии пластины за время от
τ
0
до
τ
∞
:
(
)
ж
ttCVQ −=
00
ρ
, (а)
где
ρ
и V - плотность и объем пластины.
Теплота, отданная пластиной за время от
τ
до
τ
∞
:
(
)
(
)
ж
ttCVQ −=
ρτ
,
(b)
где
(
)
τ
t
- средняя по толщине температура пластины в
момент времени
τ
. Тогда разница (а)-(b) даст количе-
ство теплоты, переданное окружающей среде за время от 0 до
τ
:
( ) ( )
( )
( )
(
)
−
−
−−=−−−=
ж
ж
жжжос
tt
tt
ttCVttCVttCVQ
0
00
1
τ
ρτρρ
.
Так как
(
)
ж
ж
tt
tt
−
−
=
0
τ
θ
, то можно записать
(
)
(
)
(
)
θρθ
−−=−= 11
00 жос
ttCVQQ . (17.8)
Учитывая выражение для локальной избыточной температуры
( )
∑
+
=
−
δ
µ
µµµ
µ
ϑϑ
τ
δ
µ
x
e
n
a
nnn
n
n
cos
sincos
sin2
2
2
0
, найдем среднюю по толщине избы-
точную температуру пластины, а затем среднюю безразмерную температуру
θ
:
( )
∫
∑
+
=
−
δ
τ
δ
µ
δ
µ
µµµ
µ
ϑ
δ
ϑ
0
0
cos
sincos
sin2
1
2
2
dx
x
e
n
a
nnn
n
n
,
( )
n
n
n
n
nn
n
n
xx
d
x
dx
x
µ
µ
δ
δ
µ
µ
δ
δ
µ
δ
µ
µ
δ
δ
µ
δ
δδ
sinsincoscos
0
00
=
=
=
∫∫
следователь-
но,
( )
∑
∞
−
+
=
1
2
0
2
2
sincos
sin2
τ
δ
µ
µµµµ
µ
ϑϑ
n
a
nnnn
n
e ,
( )
τ
δ
µ
µµµµ
µ
θ
2
2
sincos
sin2
2
1
n
a
nnnn
n
e
−
∞
+
=
∑
. (17.9)
Охлаждение (нагревание) бесконечно длинного цилиндра
Запишем уравнение теплопроводности в цилиндрических координатах при
условиях 0=
∂
∂
=
∂
∂
ϕ
T
z
T
, q
v
=0. Вводя, кроме того, избыточную температуру
(
)
ж
TrT −=
τϑ
, ,
получим
∂
∂
+
∂
∂
=
∂
∂
rrr
a
2
2
ϑϑ
τ
ϑ
1
. (a)
Как и в случае с пластиной, решение ищем в виде произведения двух функций :
(
)
(
)
.r
ψτϕϑ
= (b)
Рис.17.4
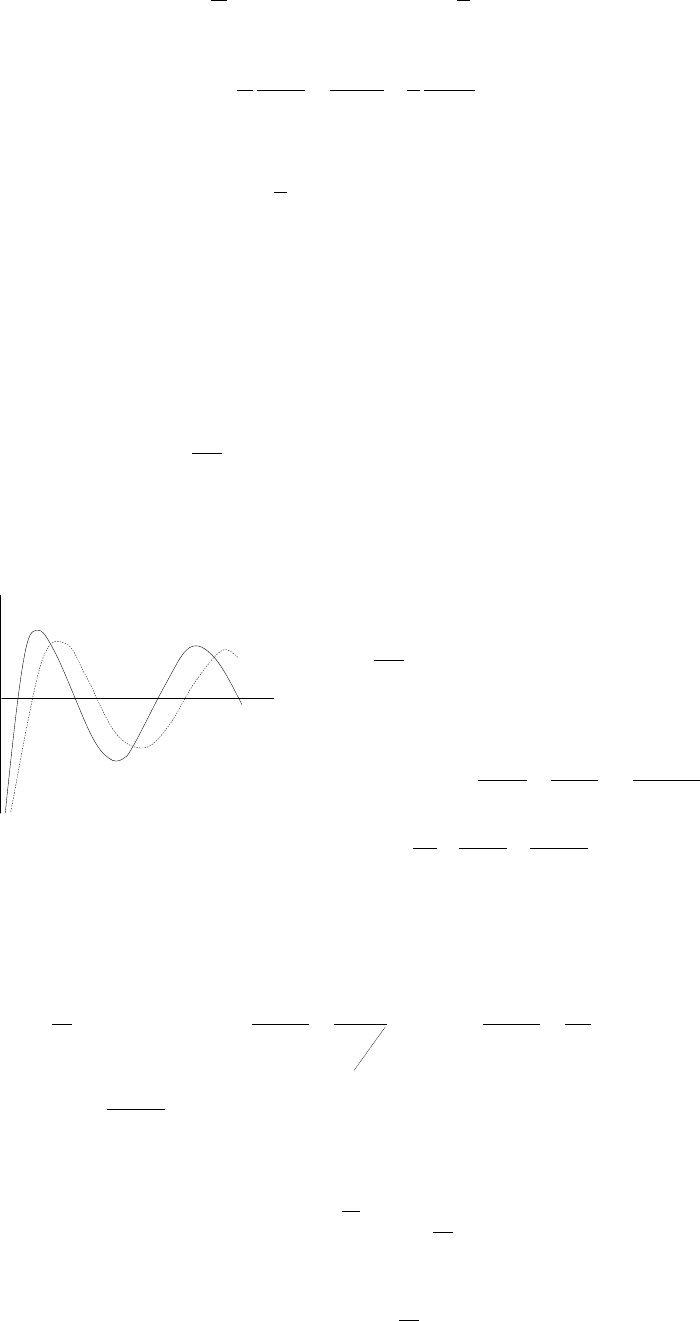
214
Подставим (b) в (а):
( ) ( ) ( ) ( ) ( ) ( )
.
11
r
r
rr
a
ψτϕψτϕψτϕ
′
+
′′
=
′
Разделим переменные:
(
)
( )
(
)
( )
(
)
( )
,
11
2
k
r
r
rr
r
a
−=
′
+
′
′
=
′
ψ
ψ
ψ
ψ
τϕ
τ
ϕ
(
)
(
)
0
2
=+
′
τϕτϕ
ak , (с)
( ) ( ) ( )
0
1
2
=+
′
+
′′
rkr
r
r
ψψψ
. (d)
(
)
(
)
(
)
(
)
krYCkrJCre
С
ak
03021
:второго ; уравнения первого Решение
2
+==
−
ψτϕ
τ
,
где J
0
– функция Бесселя первого рода нулевого порядка, Y
0
– функция Бесселя
второго рода нулевого порядка.
Частное решение уравнения (а) будет иметь вид:
(
)
(
)
(
)
krYCkrJCe
С
ak
03021
2
+=
−
τ
ϑ
. (е)
Граничные условия:
При r=0
( ) ( )( )
000
13121
0
2
=⋅+⋅−=
∂
∂
−
=
kYCkJCekС
r
ak
r
τ
ϑ
.
Так как
(
)
0
1
Y
= - ∞, а J
1
(0)=0, то
С
3
=0. Обозначая С=С
1
С
2
, получим
(
)
krJCe
ak
0
2
τ
ϑ
−
= . (k)
При r=r
0
имеем граничные условия третьего
рода
.
0
0
rr
rr
r
=
=
=
∂
∂
−
αϑ
ϑ
λ
С учетом того, что
(
)
(
)
krkJkrJ
10
−=
′
,
где
(
)
(
)
(
)
....;
6
4
2
4
2
2
1)(
222
64
222
2
0
+−+−=
krkrkr
krJ
(
)
(
)
...
6
4
2
4
2
2
)(
22
5
2
3
1
−+−=
krkrkr
krJ
можно написать
(
)
(
)
(
)
( ) ( )
.
,
0001
0001
22
krJkrkJ
krJCekrkJCe
akak
αλ
αλ
ττ
=
=−−
−−
Вводя новую переменную
0
kr
=
µ
, получим характеристическое уравнение в
виде
( ) ( )
µαµ
µ
λ
01
0
JJ
r
= ,
(
)
( )
(
)
( )
BiJ
J
r
J
J
µ
µ
µ
λ
α
µ
µ
µ
==
1
0
0
1
0
или .
Отношение
(
)
( )
µ
µ
1
0
J
J
напоминает поведение котангенсоиды с убывающим перио-
дом (рис.17.5). Окончательно, общее решение уравнения (а) будет иметь вид:
∑
∞
=
−
=
1
0
0
2
0
2
n
n
r
a
n
r
r
JeC
n
µϑ
τ
µ
.
(17.10)
Запишем
решение
при
τ
=0:
∑
∞
=
0=n
0
n0n0
c
r
r
J
µϑ
.
0
0,5
-0,5
-1,0
5
10
Y
0
(x)
Y
1
(x)
x

215
Умножим левую и правую части на
0
n0
r
r
r J
µ
и проинтегрируем от 0 до r
0
.
Для левой части уравнения можно
написать:
( )
(a),
=
n1
n
2
00
r
0
r
0
0
n
0
n0
n
00
0
n00
0 0
µ
µ
ϑ
µµ
µ
ϑ
µϑ
J
r
r
r
d
r
r
r J
r
dr
r
r
r J
=
=
⋅
∫ ∫
для правой:
∫
∫
+
0
0
r
0
r
0
0
n0
0
202
0
n0
0
101
+c
+ c
dr
r
r
J
r
r
r J
dr
r
r
J
r
r
r J
µµ
µµ
( ) ( )
( )
n
2
1n
2
0
2
0
r
0
0
n
2
0n
2
=c
0
µµµ
JJ
сr
dr
r
r
rJ
n
+
+⋅⋅⋅
∫
(b)
(здесь все члены ряда, кроме последнего,
из-за ортогональности подинтегральных функций равны нулю, а интеграл
)),()((
2
)(
2
1
2
0
0
2
2
0
axJaxJ
x
dxaxxJ
x
+=
∫
см. [31], стр. 120, ф-
ла (19)).
Приравняем ( a ) и ( b )
( ) ( ) ( )
(
)
n
2
1n
2
0
n
n1
n
0
2
c
µµµ
µ
ϑ
JJJ += , откуда
(
)
( ) ( )
( )
n
2
1n
2
0n
n10
n
2
c
µµµ
µ
ϑ
JJ
J
+
= .
Подставляя эту константу в (17.10), получим
(
)
(
)
( ) ( )
( )
( )
∑
∞
−
+
=
−
=
1=n
0
n0
2
n
n
2
1n
2
0n
n1
ж0
ж
Foexp
2
-
,
r
r
J
JJ
J
tt
trt
µµ
µµµ
µτ
θ
. (17.11)
На поверхности цилиндра (r=r
0
) имеем
(
)
(
)
( ) ( )
( )
( )
( )
∑
∞
=
−⋅
+
=
−
=
1=n
n0
2
n
n
2
1n
2
0n
n1
ж0
ж0
Foexp
2
-
,
0
µµ
µµµ
µ
τ
θ
J
JJ
J
tt
trt
rr
, (17.12)
в середине (r=0):
(
)
( ) ( )
( )
( )
Fo-exp
2
2
n
1
n
2
1n
2
0n
n1
0
µ
µµµ
µ
θ
∑
∞
=
=
+
=
n
r
JJ
J
.
(17.13)
Количество теплоты ,отдаваемое цилиндром в процессе охлаждения
Выполнив выкладки, аналогичные случаю с пластиной, получим:
(
)
( )
θ
τ
−=
−
−
−= 11
0
0
0
Q
tt
tt
QQ
ж
ж
oc
, где
(
)
(
)
ж0
2
0ж00
ttc −=−= tlrct VQ
ρπρ
,
(
)
(
)
( ) ( )
( )
∫ ∫
+
=
Σ
0 0
0 0
0
n0
n
2
1n
2
0n
2
nn1
2
0
2
0
Fo-exp
4
= 2
1
r r
rdr
r
r
J
JJ
J
r
rdr
r
πµ
µµµ
µµ
π
πθ
π
θ
. (e)
1
0
J
0
J
1
µ
µ
0
y
1
=J
0
/J
1
y
2
=
µ
/Bi
µ
1
µ
2
µ
3
µ
4
Рис.17.5
216
Рассмотрим интеграл
( )
∫∫
=
=
00
0
n1
n
2
0
0
n
0
n0
n
0
0
0
n0
rr
J
r
r
r
d
r
r
rJ
r
rdr
r
r
J
µ
µ
π
µµπ
µ
πµ
. (k)
Подставим (k) в (е)
(
)
(
)
( ) ( )
( )
∑
∞
=
+
=
1
n
2
1n
2
0
2
n
2
nn
2
1
Fo-exp4
n
JJ
J
µµµ
µµ
θ
. (17.14)
Полученные решения для пластины и цилиндра могут быть использованы для оп-
ределения температуры в данной точке в данное время как при нагревании, так и
при охлаждении тел.
Охлаждение ( нагревание ) тел конечных размеров
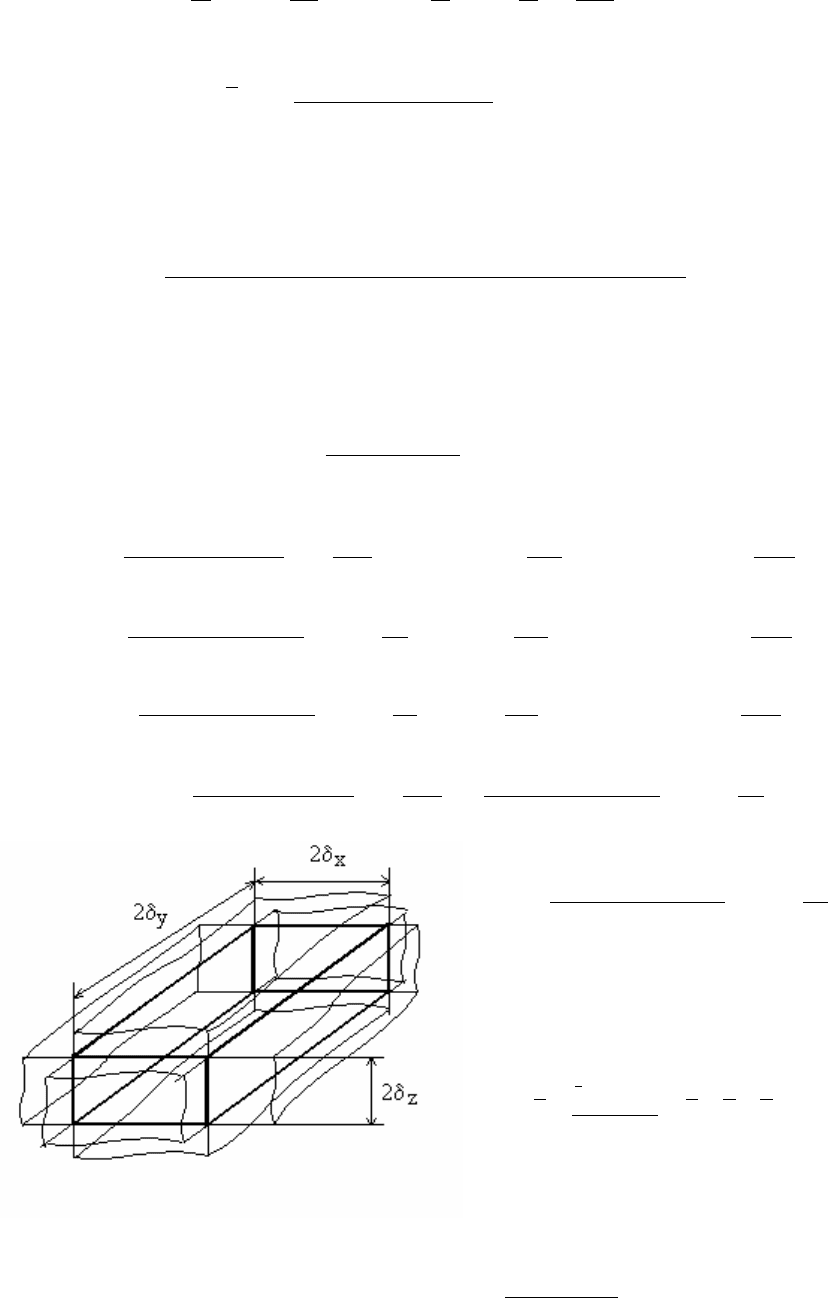
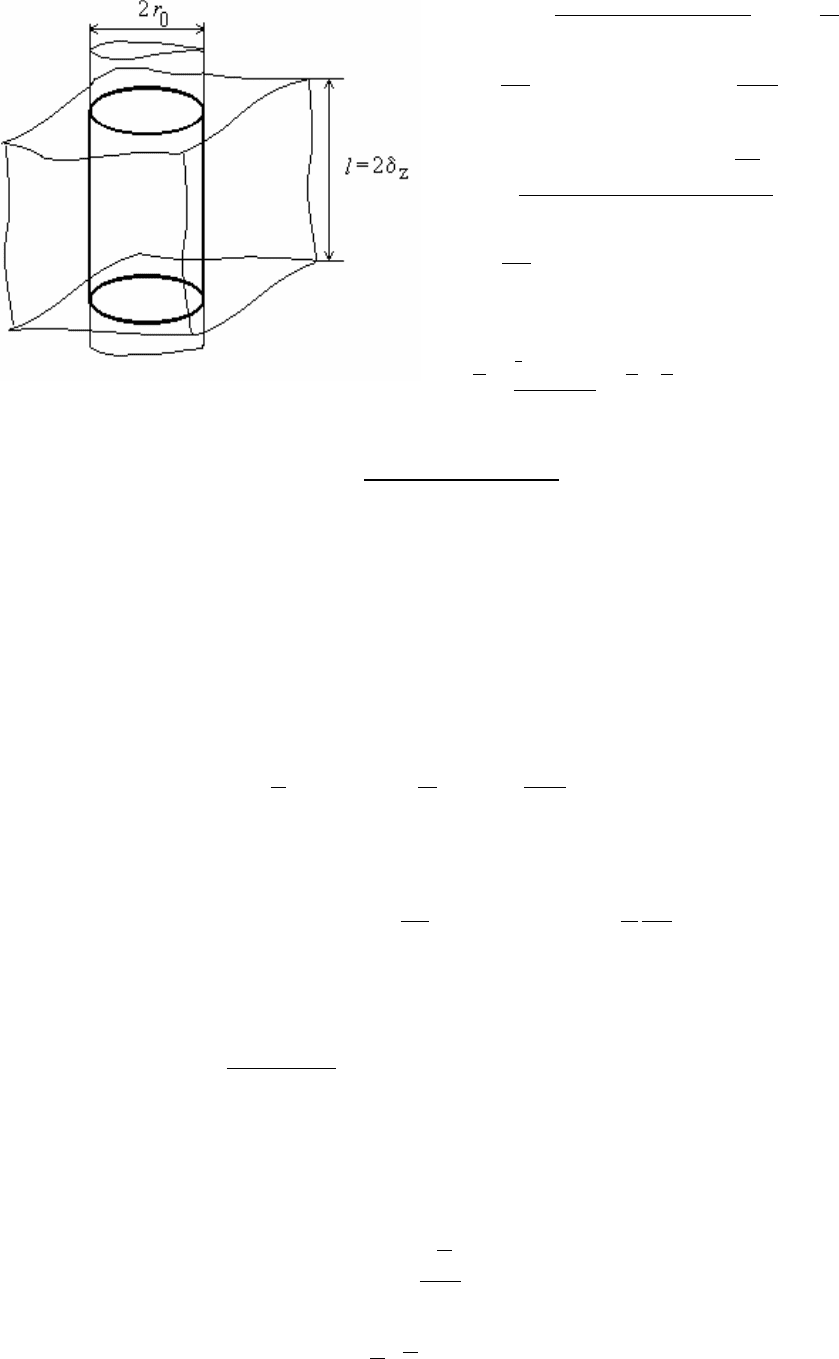
a. Охлаждение ( нагревание ) параллелепипеда.
Так как параллелепипед может рассматриваться как результат пересечения
трех бесконечных пластин (рис.17.6), то можно доказать, что решением для па-
раллелепипеда является произведение решений для бесконечных пластин с тол-
щинами 2
δ
x
, 2
δ
y
и 2
δ
z
:
(
)
zyx
0
θθθ
τ
θ
⋅⋅=
−
−
=
ж
ж
tt
tx,y,z,t
. (17.15)
Решения для бесконечных пластин имеют вид:
,cos
sincos
sin2
1=n
x
n
nnn
-Fo
n
x
2
nx
∑
∞
+
=
δ
µ
µµµ
µ
θ
µ
xe
( )
,=Bi,Bi= ,Fo
x
xx
2
x
x
λ
αδ
µ
δ
τ
f
a
=
( )
∑
∞
⋅+
=
1=n
y
n
nnn
-Fo
n
y
cos
sincos
sin2
2
ny
δ
µ
µµµ
µ
θ
µ
y
e
,
( )
λ
αδ
µ
δ
τ
y
yy
2
y
y
=Bi ;Bi= ;Fo f
a
= ,
(
)
∑
∞
⋅+
=
1=n
z
n
nnn
-Fo
n
z
cos
sincos
sin2
2
nz
δ
µ
µµµ
µ
θ
µ
z
e
;
( )
λ
αδ
µ
δ
τ
z
zz
2
z
z
=Bi ;Bi= ;Fo f
a
= ,
тогда
( )
∑∑
∞∞
×
⋅+
+
=
1=n
y
n
nnn
-Fo
n
0=n
x
n
nnn
Fo-
n
cos
sincos
sin2
cos
sincos
sin2
2
ny
2
nx
δ
µ
µµµ
µ
δ
µ
µµµ
µ
θ
µ
µ
y
exe
(
)
.cos
sincos
sin2
1=n
z
n
nnn
-Fo
n
2
nz
∑
∞
⋅+
×
δ
µ
µµµ
µ
µ
z
e
(17.16)
Среднее значение температуры
также определяется произведением
средних температур для бесконечных
пластин (см. формулу (17.9) ):
(
)
zyx
0
θθθ
τ
θ
⋅⋅=
−
−
=
ж
ж
tt
tt
.
б. Охлаждение ( нагревание ) цилин-
дра.
Для цилиндра (рис.17.7) можно на-
писать:
(
)
zr
ж0
ж
θθ
τ
θ
⋅=
−
−
=
tt
tr,z,t
, (17.17)
Рис.17.6
217
где
(
)
( ) ( )
( )
∑
∞
+
=
1=n
0
n0
n
2
1n
2
0n
-Fo
n1
r
2
n
2
r
r
J
JJ
eJ
r
µ
µµµ
µ
θ
µ
;
( )
λ
α
µ
τ
0
rr
2
0
r
Bi ;Bi = ;Fo
r
f
r
a
== ;
( )
∑
∞
+
=
1=n
nn
n
Fo-
n
sincos
cossin2
2
nz
µµµ
δ
µµ
θ
µ
n
z
z
z
e
;
( )
.Bi= ;Fo
2
z
z z
f
a
µ
δ
τ
= (17.18)
Среднюю температуру цилиндра конеч-
ных размеров находим по форму-
ле
(
)
rz
ж0
ж
tt
tt
=
θθ
τ
θ
⋅=
−
−
.
Регулярный режим
В процессе охлаждения любого тела можно выделить три стадии:
начальную, когда скорость изменения температуры внутри тела зависит от на-
чального распределения температуры в теле, условий теплообмена и физических
свойств тела; стадию охлаждения, когда процесс определяется только усло-
виями теплообмена на границе тела и среды, физическими свойствами тела
и его геометрической формой и размерами; стадию установления теплового
равновесия с окружающей средой. Анализируя решения для пластины и цилиндра
видим, что они могут быть представлены
в виде:
∑
∞
=
=
1
m-
nn
ec
n
U
τ
ϑ
,
где
под
n
U
понимается
δ
cos
n
x
µ
или
0
0
r
r
J
n
µ
;
2
2
n
=m
δ
µ
a
.
При Fo>0,3 достаточно первого члена ряда:
τ
ϑ
-m
11
ec= U (а).
Прологарифмируем и продифференцируем (а) по времени:
(
)
, mclnln
11
τϑ
−= U
( )
mln −=
∂
∂
ϑ
τ
, или m
1
−=
∂τ
∂ϑ
ϑ
, (17.19)
где m- скорость изменения относительной температуры во времени, или темп ох-
лаждения. Вторая стадия охлаждения, которая характеризуется одинаковым тем-
пом охлаждения для всех точек тела, называется регулярным режимом. Из (17.19)
следует, что
12
21
lnln
=m
ττ
ϑ
ϑ
−
−
. Темп охлаждения при регулярном режиме не зави-
сит от начального распределения температуры, а определяется условиями тепло-
обмена, физическими свойствами, геометрическими размерами и формой тела.
Определим зависимость темпа охлаждения тела от его физических свойств, гео-
метрической формы, размеров и условий теплообмена.
Напишем два уравнения:
τ
τ
ϑ
ρ
dVcdQ
V
∂
∂
= (а)
-
количество теплоты, которое идет на увеличение энтальпии,
τϑα
dFdQ
F
=
(b)
Рис.17.7
218
-количество теплоты, которое получило (отдало) тело за .
τ
d
Здесь
V
ϑ
- температура, осредненная по объему;
F
ϑ
- температура, осредненная
по поверхности. Приравнивая (а) и (b), получим:
F
V
FC
ϑα
τ
ϑ
=
∂
∂
, cVC
ρ
=
, откуда
V
F
v
V
C
F
ϑ
ϑα
τ
ϑ
ϑ
=
∂
∂
1
, или
V
F
C
F
ϑ
ϑα
=m .Введем поня-
тие коэффициента неравномерности распределения температуры
10, ≤≤=
ψ
ϑ
ϑ
ψ
v
F
.
Тогда m
C
F
ψ
α
= (17.20)
- первая теорема Кондратьева. Из (17.20) видно, какие величины влияют на
темп охлаждения. Рассмотрим случай, когда Bi
→∞
(практически Bi>100). Для
пластины можно написать:
22
2
2
2
1
2
1
2
=
==
∞=
π
δ
δ
π
δ
µ
a
a
a
m
Bi
,
где
( )
2
,
2
12
1
π
µ
π
µ
=−= n
n
.
Вводя понятие коэффициента формы тела для пластины
2
2
=
π
δ
k , получаем: kma
k
a
m
∞∞
== ;
(17.21)
- вторая теорема Кондратьева.
Для шара коэффициент формы имеет вид
2
0
1
=
r
k
π
,
для конечного цилиндра
2
2
0
405,2
1
+
=
lr
k
π
,
для параллелепипеда
2
3
2
2
2
1
1
+
+
=
lll
k
πππ
.
Вторая теорема Кондратьева часто используется для определения теплофизи-
ческих свойств различных материалов.
18. Численные методы решения задач теплопроводности
Методы решения задач теплопроводности
Определение температуры в теле даже простой формы связано с определен-
ными математическими трудностями (см. 2-х мерная стационарная теплопровод-
ность). Задача еще более усложняется, если речь идет о телах сложной формы.
В этом случае для решения задачи используются численные методы. Суть
численного метода заключается в том, что дифференциальные уравнения записы-
ваются в конечноразностной форме.
Рассмотрим тело (пластину) и разобьем его на ячейки, причем будем считать, что
масса сосредоточена в узлах, а передача теплоты происходит по нитям (рис.18.1).
Рассмотрим сначала внутренний узел.
219
Для стационарной задачи сумма тепловых потоков к данной ячейке от сосед-
них узлов равна нулю.
∑
=
→
0
0i
Q
&
. (18.1)
Так как
FgradTQ
λ
−=
&
, то тепловой поток , который получил узел "0" от узла
"1":
∆
−
∆=
→
x
TT
ybQ
01
01
λ
&
(a)
(в (а) дифференциал
dx
dT
заменен конечной разностью). Аналогично,
∆
−
∆=
→
y
TT
xbQ
02
02
λ
&
, (b)
∆
−
∆=
→
x
TT
ybQ
03
03
λ
&
, (c)
∆
−
∆=
→
y
TT
xbQ
04
04
λ
&
. (d)
Представим, что в узле “0” есть внутренний источник теплоты, тогда:
yxbqQ
vv
∆∆=
&
. (е)
Для простоты положим, что ∆
х
=
∆
у
. Сложим уравнения (a,b,c,d,e) и приравняем
сумму нулю:
0
2
04030201
=
∆
+−+−+−+−
λ
xq
TTTTTTTT
v
,
λ
2
43210
4
xq
TTTTT
v
∆
++++= ,
тогда температуру в искомом узле найдем из выражения:
4
2
4321
0
λ
xq
TTTT
T
v
∆
++++
= . (18.2)
При q
v
=0 получаем :
4
4321
0
TTTT
T
+
+
+
= . (
18.2а)
Чем меньше размер ячейки
(
)
y x ∆×∆ , тем
точнее будет результат. Пусть теперь узел
находится на поверхности тела (рис.18.2).
Положим, что ∆
х
=∆
у
, тогда
(
)
(
)
( )
,0)(
2
2
0
03
0201
=−∆+
∆
−
∆
+
+
∆
−
∆
+
∆
−
∆
TTyb
y
TT
x
b
y
TT
x
b
x
TT
yb
ж
αλ
λλ
( ) ( )
.0
2
2
0030201
=−
∆
+−+−+− TT
x
TTTTTT
ж
λ
α
Рис
.18.1
220
,022
22
00
30201
=−+−
−
+
−
+
−
BiTBiTT
TTTTT
ж
,2224
32100 ж
BiTTTTBiTT +++=+
( )
Bi
BiTTTT
T
ж
+
+
+
+
=
22
22
321
0
. (18.3)
Узел
находится
на
вершине
внешнего
угла
)( yx
∆
=
∆
(
рис
.18.3).
(
)
( )
( )
,0
2
222
02
0
01
=
∆
−
∆
+
+−
∆
+
∆
+
∆
−
∆
x
TT
x
b
TT
xx
b
x
TT
x
b
ж
λ
αλ
( )
0
2
02001
=−+−
∆
+− TTTT
x
TT
ж
λ
α
,
,022
02001
=−+−+− TTBiTBiTTT
ж
,222
2100 ж
BiTTTBiTT ++=+ .
)1(2
2
21
0
i
ж
B
BiTTT
T
+
+
+
=
Если
бы
угол
был
теплоизоли
-
рован
,
т
.
е
. 0
=
α
,
тогда
Bi=0 ,
а
2
21
0
TT
T
+
= .
Узел
находится
в
вершине
внутреннего
угла
yx
∆
=
∆
,
∑
=
→
0
0
i
Q
&
,
(
)
(
)
(
)
( )
( )
,0
222
2
0
04
030201
=−
∆
+
∆
+
∆
−
∆
+
+
∆
−
∆+
∆
−
∆+
∆
−
∆
TT
xx
b
x
TT
xb
x
TT
xb
x
TT
xb
x
TT
x
b
ж
α
λ
λλλ
,0Bi2Bi2
2222
0
ж
0
4030201
=−+−
−
+
−
+
−
+
−
TTT
TTTTTTT
,Bi222Bi26
ж
432100
TTTTTTT ++++=+
)Bi3(2
Bi222
ж
4321
0
+
+
+
+
+
=
TTTTT
T (18.4)
.
Для
теплоизолированного
внутреннего
угла
(
рис
.18.4)
будем
иметь
.
3
)(
2
1
3241
0
TTTT
T
+++
=
Возможные
способы
численного
решения
задач
теплопроводности
рас
-
смотрим
на
примере
расчетной
области
с
небольшим
числом
узлов
.
Пусть
требует
-
ся
рассчитать
распределение
температу
-
ры
в
плоском
квадратном
теле
,
одна
из
сторон
которого
теплоизолирована
,
на
двух
заданы
граничные
условия
первого
рода
,
на
четвертой
-
условия
третьего
ро
-
да
(
см
.
рис
.18.5).
Рис
.18.2
Рис
.18.3
Рис
.18.4
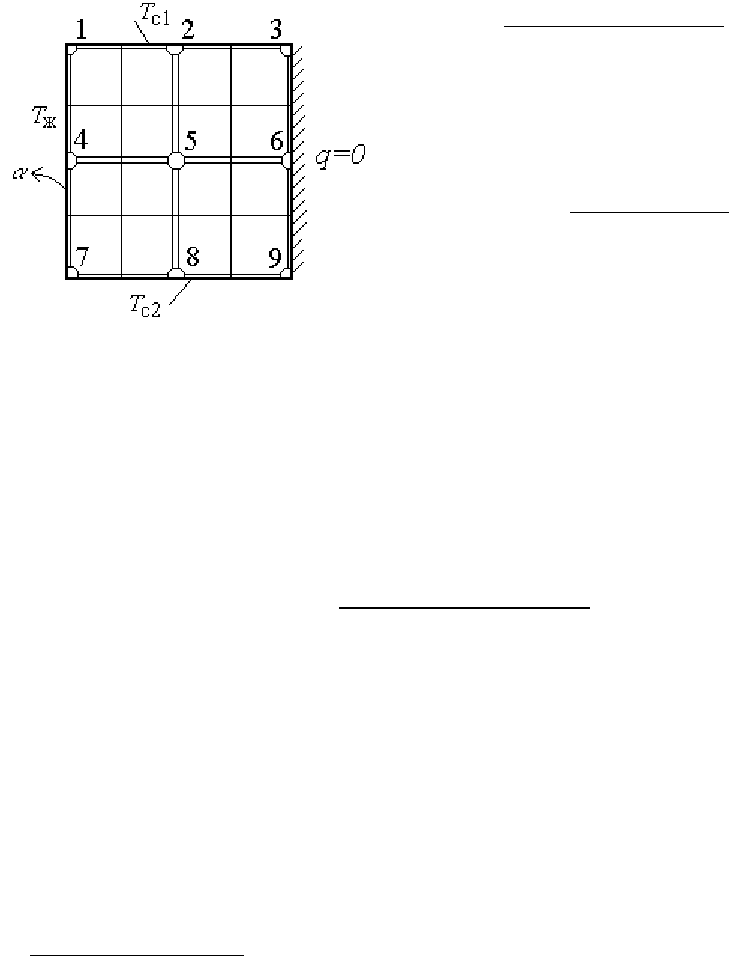
221
1.
Итерационный
метод
.
Для
каждого
узла
составляется
уравне
-
ние
вида
(18.2)...(18.4),
которое
разреша
-
ется
затем
относительно
температуры
в
текущем
узле
.
Так
,
для
узла
5
имеем
:
04
58624
=−+++ TTTTT ,
4
8624
5
TTTT
T
+++
= .
Значения
температур
в
соседних
узлах
бе
-
рутся
с
предыдущей
итерации
.
В
начале
счета
во
внутренних
узлах
принимаются
,
как
правило
,
нулевые
значения
температу
-
ры
.
Процесс
счета
продолжается
до
тех
пор
,
пока
температуры
во
всех
узлах
рас
-
четной
сетки
не
совпадут
с
заданной
точ
-
ностью
со
значениями
на
предыдущей
итерации
.
Этот
метод
называется
методом
Гаусса
.
Число
итераций
может
быть
уменьшено
,
если
применить
метод
Гаусса
-
Зейделя
,
в
котором
при
определении
температуры
в
очередном
узле
используется
температура
,
только
что
найденная
в
соседнем
узле
.
2.
Релаксационный
метод
.
Записав
уравнения
для
каждого
узла
,
вместо
нуля
в
правой
части
следует
по
-
ставить
остаточный
член
558624
4 RTTTTT =−+++ .
Исходя
из
общих
представлений
о
процессе
,
задаем
начальные
значения
температур
в
узлах
,
подставляем
их
в
уравнения
и
определяем
остаточные
члены
.
Находим
узел
,
в
котором
остаточный
член
имеет
наибольшую
величину
и
изменя
-
ем
температуру
в
узле
так
,
чтобы
остаточный
член
стремился
к
нулю
,
при
этом
изменятся
температуры
в
соседних
узлах
.
Снова
ищется
уравнение
с
наибольшим
остаточным
членом
,
и
т
.
д
.
Этот
процесс
продолжается
до
тех
пор
,
пока
макси
-
мальное
значение
остаточного
члена
не
станет
равным
нулю
с
заданной
погреш
-
ностью
.
3.
Матричный
метод
.
Суть
метода
-
обращение
матрицы
на
основе
уравнений
,
записанных
для
каждого
узла
расчетной
сетки
=++++
+
=+++
.bta tatata
b=ta +ta+ta+ta
bta+ tatata
nnnn3n32n21n1
2n2n323222121
1n1n313212111
L
LLLLLLLLLLLLLL
L
L
В
матричном
виде
:
AT =B,
где
nn n3n2n1
2n232221
1n131211
a aaa
a aaa
a aaa
=A
L
LLLLLL
L
L
;
n
3
2
1
t
t
t
t
= T
;
n
3
2
1
b
b
b
b
= B
.
Решение
в
матричной
форме
имеет
вид
CBB A = T
-1
= ,
Рис
.18.5
