Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.


242
при
0= , 0= 0=
x
awy ⇒
,
при
32
++=
δδδδ
dcbwy=
∞
. (d)
Кроме
того
,
при
0=
=y
δ
δ
dy
dw
y=
,
⇒
03+2+
2
=
δδ
dcb
. (e)
Запишем
уравнение
движения
вдоль
пластины
для
стационарного
режима
в
виде
:
2
x
2
y
w
y
w
w
x
w
w
x
y
x
x
∂
∂
ν
∂
∂
∂
∂
=+
.
При
0= , 0=: 0=
x y
w wy
,
поэтому
0
2
2
=
y=0
x
y
w
∂
∂
,
тогда
из
(
с
)
следует
,
что
с
=0.
Кроме
того
,
при
y=
δ
3
δδ
d=bw +
∞
, (k)
0=3
2
δ
db+
(
см
. (
е
)) . (m)
Подставим
(m)
в
(k)
тогда
33
-3=
δδ
+ddw
∞
,
откуда
3
-0,5=
δ
∞
w
d
. (p)
Подставляя
(p)
в
(m) ,
получим
δ
∞
w
b
1,5= .
Таким
образом
,
закон
изменения
скорости
в
пограничном
слое
имеет
вид
( )
3
5,05,1
−=
∞∞
δδ
y
w
y
wyw
x
, (22.3)
или
(
)
3
5,05,1
−=
∞
δδ
yy
w
yw
x
. (22.3a)
Подстановка
полученного
профиля
скорости
в
интеграл
толщины
потери
импульса
дает
δδ
δ
0,139 1
0
**
≈
−=
∫
∞∞
dy
w
w
w
w
xx
, (22.4)
тогда
2
ρ
139,0
∞
=
wdx
d
w
τ
δ
. ( * )
Так
как
δ
∞
=
w
dy
dw
y=0
x
5,1 ,
то
из
соотношения
для
напряжения
трения
y=0
x
dy
dw
=
w
µτ
,
получим
δ
µ
τ
∞
=
w
5,1
w
. ( ** )
Подставим
( ** )
в
( * ):
2
5,1139,0
∞
∞
=
w
w
dx
d
ρδ
µ
δ
,
dx
w
d
∞
⋅=
ρ
µ
δδ
139,0
5,1
,
или
x
w
∞
⋅=
ρ
µδ
139,0
5,1
2
2
,
откуда
видно
,
что
δ
(
х
)
∼
х
0,5
,
т
.
е
.
толщина
пограничного
слоя
пропорциональна
квадратному
корню
расстояния
от
начала
пластины
.
Переписав
последнее
выражение
в
виде
µ
ρ
δ
∞
⋅=
xw
x
2
2
139,0
3
,
получим
закон
изменения
толщины
гидродинамического
пограничного
слоя
вдоль
пластины
243
( )
5,0
x
Re
65,4
x
x =
δ
,
(22.5)
где
ν
xw
∞
=
x
Re .
Найдем
значение
локального
коэффициента
трения
с
f
,
учитывая
выражение
для
касательного
напряжения
трения
2
2
w
∞
=
w
c
f
ρ
τ
:
,
2
5,1
2
22
∞
∞
∞
==
w
w
w
c
w
f
δρ
µ
ρ
τ
x
xx
f
wxw
c
Re
Re
645,0
65,4
Re3
3
5,05,0
===
∞∞
ρ
µ
δρ
µ
,
или
0,5
x
Re
645,0
=
f
c
. (22.6)
Сила
аэродинамического
сопротивления
пластины
lbF
wсопр
τ
2
=
, (22.7)
где
w
τ
2
2
∞
=
w
c
f
ρ
-
среднее
напряжение
трения
, l -
длина
, b -
ширина
пластины
.
Средний
по
длине
коэффициент
трения
определим
по
формуле
( )
∫∫
==
∞
ll
ff
dx
xw
l
dxxc
l
c
0
0,55,0
0
Re
1,29
=
ν
645,011
, (22.8)
где
число
Рейнольдса
подсчитано
по
скорости
невозмущенного
потока
и
длине
пластины
ν
lw
∞
=Re .
Тепловой
пограничный
слой
.
Уравнение
Кружилина
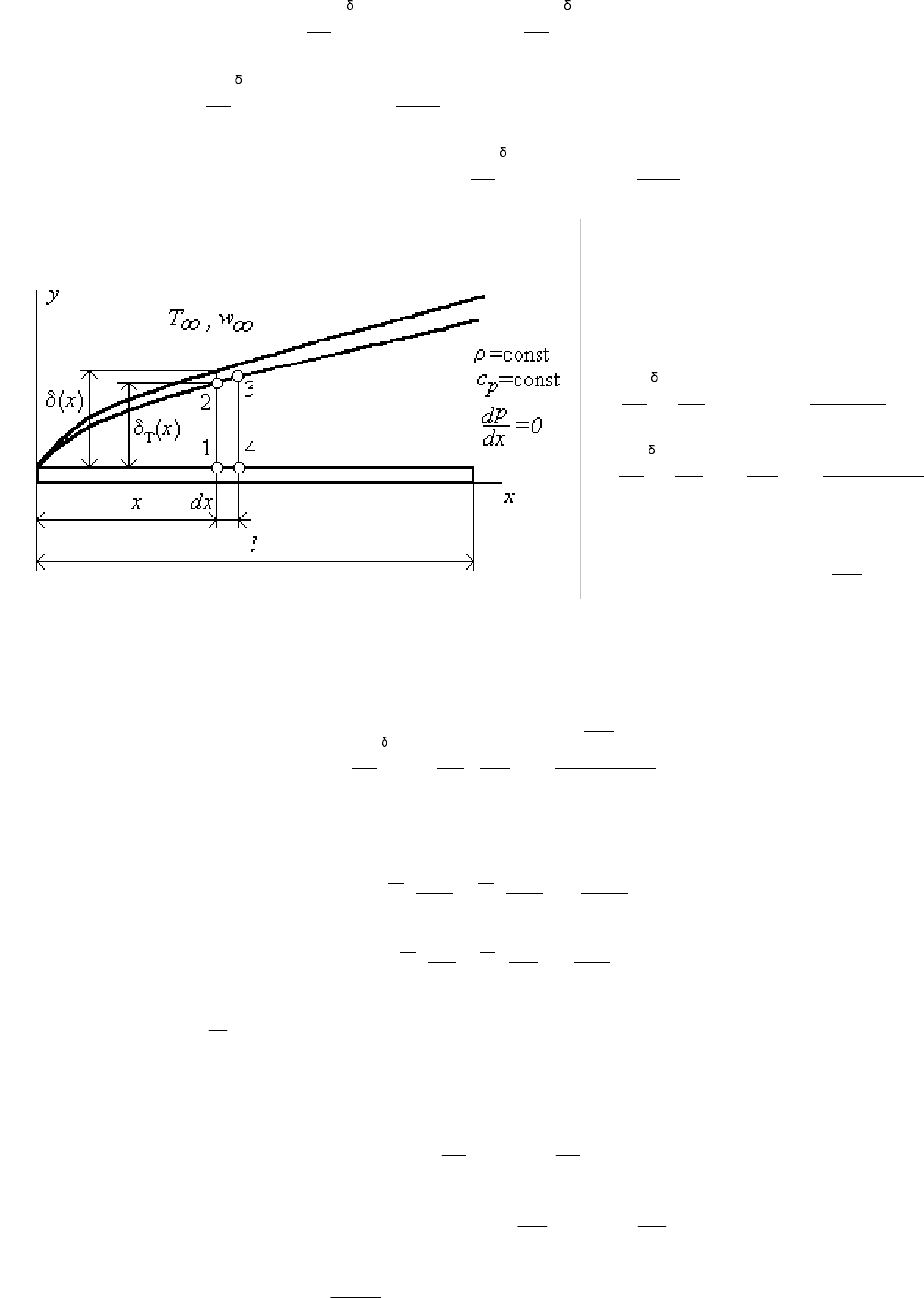
Составим
уравнение
теплового
баланса
для
неподвижного
элементарного
объема
1-2-3-4,
выделенного
в
тепловом
пограничном
слое
.
Будем
полагать
,
что
Pr>1,
т
.
е
.
тепловой
слой
лежит
внутри
гидродинамического
, h= 1
т
<
δ
δ
(
рис
.22.2).
Запишем
потоки
энтальпии
,
переносимые
через
грани
выделенного
элементарного
объема
на
единицу
ширины
потока
.
Грань
1-2 :
( )
∫
⋅
T
0
px
dy T cy w
1
ρ
,
при
const= const,=
p
c
ρ
получаем
∫
T
0
xp
T dy w c
ρ
. (
а
)
Поток
энтальпии
,
которую
внесет
невозмущенный
поток
через
грань
2-3:
dxdyw
dx
d
cT
T
0
xp
∫
∞
ρ
, (b)
энтальпия
,
которую
вынесет
поток
через
грань
3-4
∫ ∫
+
T T
0 0
xpxp
dxTdyw
dx
d
cTdyw c
ρρ
. (
с
)
Будем
считать
,
что
Т
w
> T
∞
,
т
.
е
.
через
грань
1-4
от
стенки
к
элементарному
объему
подводится
тепловой
поток
dxq
w
⋅⋅1 ,
тогда
уравнение
теплового
баланса
(a)+(b)-(
с
)+q
w
dx
= 0
принимает
вид
244
dxdx=qdyw
dx
d
cdx-TTdyw
dx
d
c
w
0
xp
0
xp
TT
∫∫
∞
ρρ
,
или
( )
∫
∞
T
0
p
w
xx
c
q
dy=wT-Tw
dx
d
ρ
.
Переписав
последнее
уравнение
в
виде
( )
∫
∞
T
0
p
w
x
c
q
dy=wT-T
dx
d
ρ
, (22.9)
получим
уравнение
Кружилина
.
Вводя
избыточную
температуру
w
TT
−
=
ϑ
,
преобразуем
(22.9)
к
безразмерной
форме
:
(
)
(
)
∞∞∞
−=−
ϑϑ
ww
-TTT-T=T-T ,
∫
∞∞
−
T
0
p
w
x
c
q
dy=w
dx
d
1
ϑρϑ
ϑ
,
∫
∞∞∞∞
−
T
0
p
wx
w c
q
dy=
w
w
dx
d
1
ϑρϑ
ϑ
.
(22.10)
Так
как
0
=
−=
y
w
dy
d
q
ϑ
λ
,
то
уравнение
(22.10)
принимает
вид
∫
∞∞
=
∞∞
−
T
0
p
y
x
w c
dy
d
dy=
w
w
dx
d
0
1
ϑρ
ϑ
λ
ϑ
ϑ
. (d)
Перепишем
безразмерные
уравнения
движения
(19.9)
и
энергии
(19.10)
для
пограничного
слоя
на
пластине
:
2
2
Re
y
w
y
w
w
x
w
w
xx
y
x
x
∂
∂
=
∂
∂
+
∂
∂
,
2
2
Pe
yy
w
x
w
yx
∂
∂
=
∂
∂
+
∂
∂
θθθ
.
Так
как
Pe = Re⋅Pr,
то
при
Pr = 1
получаем
Pe = Re.
Следовательно
,
записанные
выше
уравнения
для
(
)
yw
x
и
)
(
y
=
θ
идентичны
и
распределение
температуры
в
тепловом
пограничном
слое
подобно
распределению
скорости
в
динамическом
пограничном
слое
.
Тогда
можно
записать
аналогично
(22.3):
( )
∞∞
−=
ϑ
δ
ϑ
δ
ϑ
3
тт
5,05,1
yy
y . (22.11)
Возьмем
производную
от
(22.11)
при
у=0 :
т
0
5,1
δ
ϑ
ϑ
∞
=
=
∂
∂
y
y
.
Теперь
правую
часть
(d)
можно
переписать
в
виде
т
5,1
δ
∞
w
a
.
Взяв
интеграл
в
левой
части
уравнения
(d),
получим
Рис.22.2
245
∫
≈
−
∞∞
T
0
x
hdy
w
w
2
15,01
δ
ϑ
ϑ
, (e)
где
δ
δ
т
=h .
Подставив
значения
интеграла
и
производной
0
=
∂
∂
y
y
ϑ
в
(d)
най
дем
,
что
(
)
δ
δ
hw
a
dx
hd
∞
= 5,115,0
2
.
После
выполнения
дифференцирования
,
можно
написать
(
)
dx
w
a
dhhdhh
∞
=+ 102
2
δδδ
.
Если
тепловой
и
гидродинамический
слои
зарождаются
в
одной
точке
при
х=0,
то
0=
dx
dh
,
тогда
∞
=
w
a
dx
dh
10
3
δδ
. (f)
При
выводе
уравнения
Кармана
было
показано
,
что
∞∞
≈=
wwdx
d
ρ
µ
ρ
µ
δ
δ
10
139,0
5,1
,
тогда
(f)
примет
вид
ah =
ρ
µ
3
,
откуда
3
Pr
1
=h .
Так
как
δδ
h=
т
,
то
с
учетом
(22.11),
получим
33,05,0
т
PrRe
65,4
)(
x
x
x =
δ
. (22.12)
Теплоотдача
от
плоской
пластины
при
ламинарном
режиме
течения
Воспользуемся
граничными
условиями
III
рода
для
определения
коэффициента
теплоотдачи
на
пластине
( )
(
)
0
=
∞
−
−=−
y
w
wx
dy
TTd
TT
λα
,
( )
(
)
0
=
∞
−
−=−−
y
w
wx
dy
TTd
TT
λα
,
0
=
∞
=
y
x
dy
d
ϑ
λϑα
,
но
T
y
dy
d
δ
ϑ
ϑ
∞
=
=
5,1
0
,
тогда
T
x
δ
λ
α
5,1= . (22.13)
Подставляя
(22.12)
в
(22.13),
получим
зависимость
локального
коэффициента
теплоотдачи
от
режимных
параметров
потока
и
физических
свойств
жидкости
33,0
5,0
Pr
65,4
Re5,1
x
x
x
λ
α
=
,
или
в
критериальном
виде
33,05,0
PrRe323,0Nu
x
x
x
x
==
λ
α
. (22.14)
Критериальное
уравнение
справедливо
при
(
)
5
кр
102...1ReRe
⋅=<
x
.
Определим
среднее
значение
коэффициента
теплоотдачи

246
( )
lx
ll
dx
x
xw
l
dxx
l
=
∞
=
==
∫∫
α
ν
λ
αα
2Pr
65,4
5,1
11
0
33,0
5,0
0
,
откуда
33,05,0
PrRe646,0Nu ==
λ
α
l
, (22.15)
где
ν
lW
∞
=Re .
Отметим
,
что
формула
для
x
α
при
x=0
дает
бесконечное
значение
коэффициента
теплоотдачи
:
∞
=
=0x
α
.
Тепловой
поток
,
отдаваемый
пластиной
окружающей
среде
,
определим
из
уравнения
(
)
lbTTQ
w ∞
−=
α
2
&
.
Связь
между
коэффициентами
теплоотдачи
и
трения
,
аналогия
Рейнольдса
Введем
критерий
Стентона
как
соотношение
между
тепловыми
потоками
,
переносимыми
поперек
и
вдоль
течения
:
∞
=
wc
p
x
ρ
α
x
St
.
Умножим
числитель
и
знаменатель
на
произведение
λµ
x :
PrRe
Nu
St
x
x
x
p
x
p
x
c
xw
x
x
x
wc
=
⋅
=⋅⋅⋅=
∞∞
λ
µ
µ
ρ
λ
α
µ
µ
λ
λ
ρ
α
.
Таким
образом
,
PrRe
Nu
St
x
x
x
= .
Подставляя
значение
числа
Nu
х
из
критериального
уравнения
теплоотдачи
для
пластины
,
получим
3
2
5,0
3
1
5,0
Pr
Re
323,0
PrRe
PrRe323,0
St
−
==
xx
x
x
,
но
2Re
323,0
5,0
x
f
x
c
= (
см
.
формулу
(22.6)).
Тогда
3
2
Pr
2
St
−
=
x
f
x
c
(22.16)
Таким
образом
,
установлена
связь
между
локальными
коэффициентами
теплоотдачи
и
трения
для
пластины
,
получившая
название
аналогии
Рейнольдса
3
2
Pr
2
−
∞
=
x
f
p
x
c
wc
ρ
α
.
Аналогия
Рейнольдса
позволяет
по
известным
гидродинамическим
характеристикам
течения
определять
его
тепловые
характеристики
.
Зная
коэффициент
трения
из
гидродинамического
исследования
,
можно
найти
коэффициент
теплоотдачи
.
Турбулентный
пограничный
слой
При
обтекании
пластины
жидкостью
вначале
формируется
ламинарный
пограничный
слой
,
в
котором
теплота
передается
за
счет
теплопроводности
(
на
молекулярном
уровне
).
На
некоторой
координате
,
когда
Re=Re
.кр
,
он
теряет
устойчивость
и
переходит
в
турбулентный
пограничный
слой
с
ламинарным
подслоем
,
где
скорость
меняется
по
линейному
закону
.
Выделим
мысленно
в

247
турбулентной
части
пограничного
слоя
элементарную
площадку
(
см
.
гл
.18,
рис
.19.3)
и
рассмотрим
процесс
передачи
теплоты
через
нее
.
Напряжение
трения
,
действующее
на
площадку
,
и
плотность
теплового
потока
запишем
в
виде
(
)
xxly
www −
′
=
ρτ
тб
, (
а
)
(
)
lpy
TTcwq −
′
=
ρ
тб
(
в
)
(
здесь
температура
и
скорость
осреднены
по
времени
, Tw
x
,
и
lxl
Tw , -
скорость
и
температура
соответственно
на
координате
у
и
ly
′
+
).
Выразим
из
(
а
):
( )
xxl
y
ww
w
−
=
′
тб
τ
ρ
и
подставим
в
(
в
)
( )
(
)
lp
xxl
TTc
ww
q −
−
=
тб
тб
τ
,
откуда
(d)
(
)
p
xxl
l
c
wwq
TT
тб
тб
τ
−
=−
. (e)
Рассмотрим
ламинарный
подслой
:
const
лп
===
y
w
dy
dw
xx
µµτ
, (k)
(
)
const
лп
==−=−=
ww
qTT
ydy
dT
q
λ
λ
. (m)
Для
границы
между
ламинарной
и
турбулентной
частями
пограничного
слоя
со
стороны
ламинарного
подслоя
можно
написать
:
( )
гр
гр
гр
лп
, TT
w
q
w
w
w
w
w
−==
µ
λτ
τ
µ
δ
,
w
w
w
wq
TT
λτ
µ
гр
гр
=− . (n)
Мысленно
будем
передвигать
площадку
вниз
до
тех
пор
,
пока
x
w
не
станет
равной
гр
w ,
а
гр
TT = ,
тогда
вместо
(e)
можно
написать
:
(
)
.
гр
гр
pw
xlw
l
c
wwq
TT
τ
−
=− (
р
)
Сложим
(n )
и
(p)
(
)
pw
xlw
w
w
lw
c
wwqwq
TT
τλτ
µ
гргр
−
+=− .
Умножим
левую
и
правую
части
уравнения
на
α
x
,
а
затем
разделим
на
q
w
( )
(
)
,
гргр
x
pw
xlw
x
w
w
lwx
c
wwqwq
TT
α
τ
α
λτ
µ
α
−
+=−
(
)
,1
гргр
x
pw
xl
x
w
c
www
α
τ
α
λτ
µ
−
+=
,11
гргр
−+=
xlxl
p
pw
xxl
w
w
w
cw
c
w
λ
µ
τ
α
,1)1(Pr1
гр
+−=
xlpw
xxl
w
w
c
w
τ
α
но
,
2
2
xl
x
fw
w
c
ρ
τ
=
тогда
( )
+−= 11Pr
ρ
1
гр
xl
p
2
xl
x
f
xxl
w
w
c
2
w
c
w
α
,
pxl
xx
f
cw
c
ρ2
α
=
( )
,11Pr
гр
+−
xl
w
w
x
St
2
=
x
f
c
( )
+−
11Pr
гр
xl
w
w
,

248
или
( )
1
гр
x
11Pr
2
St
−
+−=
xl
x
f
w
w
c
,
(22.17)
где
.
2
St 1=Pr при ,
3
1
; St
x
гр
x
x
f
xlxlp
x
c
w
w
wc
=≈=
ρ
α
Таким образом, установлена связь между коэффициентом теплоотдачи и трения в
турбулентном пограничном слое.
Обтекание пластины при турбулентном режиме течения
Рассмотрим интегральное соотношение Кармана
∞
∞∞
=
−
∫
2
ρ
1
тб
w
dy
w
w
w
w
dx
d
w
0
xx
τ
. (a)
В дальнейших выкладках опустим знак осреднения, все параметры будем считать
осредненными по времени.
Закон изменения скорости в турбулентном пограничном слое может быть
представлен формулой
n
1
т
δ
=
∞ б
x
y
w
w
, (b)
n = 7...9, чем выше число Re, тем больше n.
Так как напряжение трения на стенке связано с производной скорости
( )
0
тб
μμ
=
+=
y
x
w
dy
dw
τ
, то при использовании профиля (b) получается
τ
w
=∞, что не отвечает действительности. Поэтому
τ
w
берут из опытных данных. В
частности, Блазиус получил, что при
∞
∞
=
ν
Re
xw
x
=10
5
…10
7
4
1
2
Re
1
0228,0
=
∞
δ
ρτ
w
w
, (d)
где
∞
∞
=
ν
δ
δ
тб
Re
w
. Полагая n=7, находим
∫
=
−
∞∞
тб
0
тб
δ
72
7
1
dy
w
w
w
w
xx
. (e)
Подставим (d) и (e) в (a):
4
1
тб
2
2
тб
δρ
ρ0228,0
δ
72
7
=
∞
∞
∞
∞
w w
w
dx
d
ν
.
Разделяя переменные и интегрируя, получим закон изменения толщины турбулентного
динамического пограничного слоя по длине пластины
∫ ∫
⋅
=
∞
∞
тб
0 0
4
1
тб
4
1
тб
7
0,022872
δ
ν
δδ
dx
w
d
x
, x
w
4
1
4
5
тб
235,0
5
4
=
∞
∞
ν
δ
,
x
w
4
1
4
5
тб
4
5
235,0
⋅=
∞
∞
ν
δ
, 293,0
5
4
4
1
тб
=
∞
∞
x
w
ν
δ
.
249
Из формулы видно, что толщина турбулентного динамического пограничного слоя
растет быстрее, чем ламинарного т.к. δ
x
∼x
0,8
. Представим закон нарастания толщины в
виде зависимости от локального числа Рейнольдса :
x
xw
x
x
x
w
5
1
5
1
5
1
5
4
4
1
тб
37,037,0
=⋅
=
∞∞
∞
ν
ν
δ
,
( )
0,2
x
тб
Re
37,0 x
x =
δ
. (22.18)
Определим локальный коэффициент трения c
fx
4
1
тб
2
2
2
2
δρ
ρ0228,02
ρ
2
2
⋅
==⇒=
∞
∞
∞
∞
∞
∞
w w
w
w
c
w
c
w
x
f
x
fw
ν
τ
ρ
τ
,
,
1
ν
37,0
046,0
0,37
Re
046,0
δ
046,0
4
1
5
1
4
1
4
1
5
1
x
4
1
4
1
тб
=
=
=
∞
∞
∞
∞
∞
∞
∞
∞
x
xw
wxww
c
x
f
ν
νν
4
1
5
1
0592,0
⋅
=
∞
∞
∞
∞
xw
xw
c
x
f
ν
ν
,
0,2
x
Re
0592,0
=
x
f
c
. (22.19)
Найдем среднее по длине пластины значение коэффициента трения:
( )
0,2
0
Re
074,0
4
51
===
=
∫
lx
x
f
l
x
ff
cdxxc
l
c
. (22.20)
Сила сопротивления пластины турбулентному потоку
2
l2=
2
∞
⋅
w
clT
f
ρ
. Учитывая
соотношение
PrRe
Nu
St
x
x
x
= , получим критериальное уравнение для локальной теплоотдачи
при турбулентном обтекании пластины:
3
1
5
4
x
3
1
x
5
1
x
x
3
2
xxx
PrRe0296,0PrRe
Re2
0592,0
PrRePr
2
PrReStNu ====
−
x
f
c
,
33,00,8
xx
PrRe0296,0Nu
=
. (22.21)
Вводя средний коэффициент теплоотдачи
( )
∫
=
l
x=l
dx=x
l
0
α
4
5
α
1
α
и число Рейнольдса
∞
∞
ν
lw
=Re , подсчитанное по длине пластины и скорости набегающего потока, получим
критериальное уравнение для определения среднего коэффициента теплоотдачи
33,00,8
PrRe037,0
α
Nu ==
∞
λ
l
. (22.22)
Допустим, что Т
w
>T
∞
, тогда тепловой поток, передаваемый пластиной потоку жидкости
(
)
∞
-TT lb=Q
w
α2
&
, Вт.
Количество теплоты, отданное за время
τ
QQ=
τ
&
, Дж.

250
Течение в трубах
Связь между коэффициентами трения и сопротивления
Рассматривая уравнение движения
ρµ
τ
ρ
+gwp +
d
wD
2
r
r
∇−∇=
для безинерционного течения, т.е. когда 0=
τ
d
wD
r
, и пренебрегая гравитационными силами,
запишем уравнение силового баланса для элементарного объема pw= ∇∇
2
µ
(рис.22.3),
откуда для течения в трубе получим dxDdp
D
w
πτ
π
=
4
2
. Согласно формуле Дарси,
2
ρ
2
w
D
dx
dp=
ξ
. Учитывая, что
2
ρ
,
4
= ,
22
w
c
D
F
F
G
=w
fw
=
τ
π
ρ
,
получаем
4
ξ
=
f
c , (22.23)
где
ξ
- коэффициент сопротивления. Таким образом, из формулы видно, что
коэффициент трения меньше коэффициента сопротивления в четыре раза.
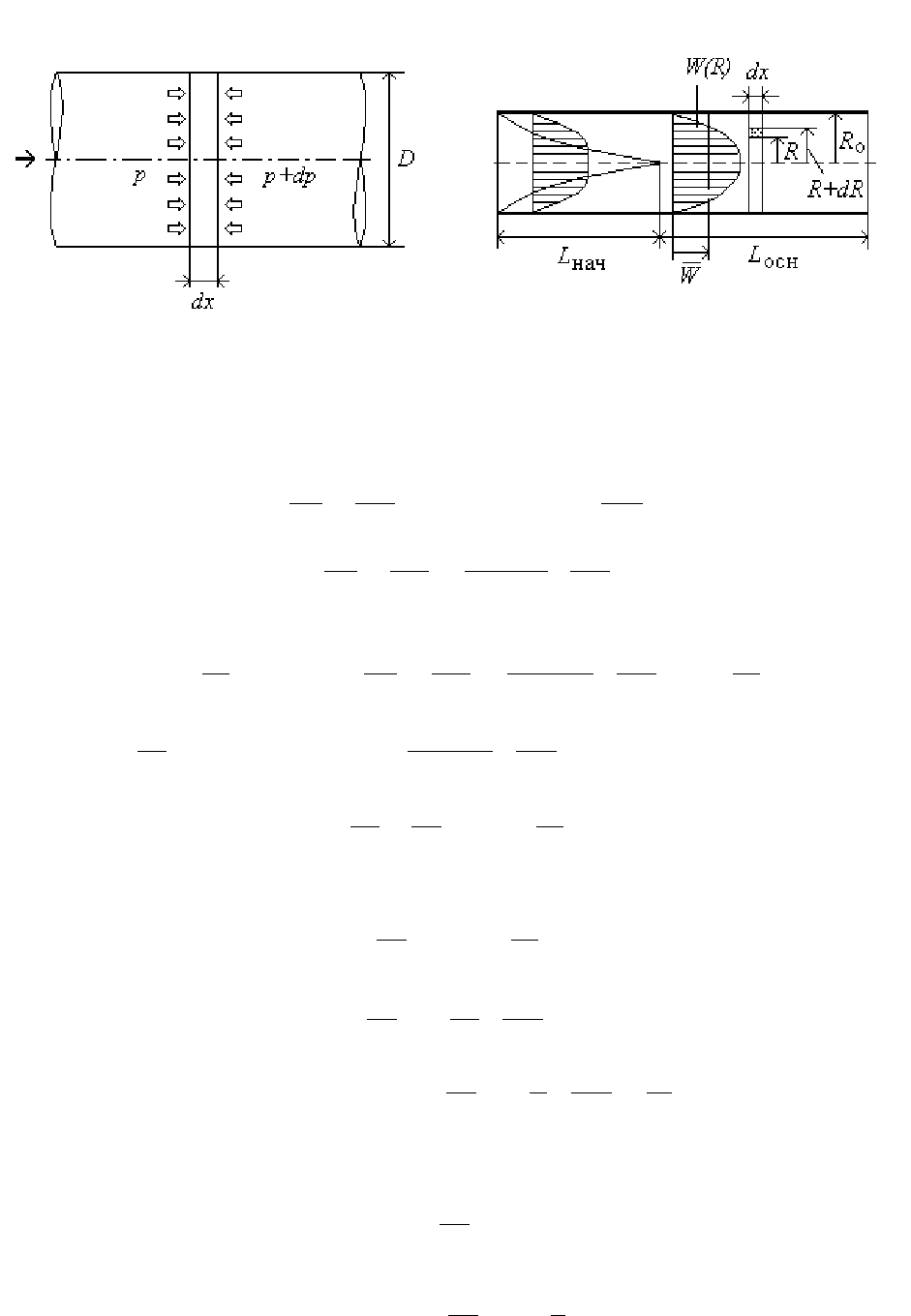
Теплоотдача в трубе при ламинарном режиме течения
При входе потока в трубу формируется
пограничный слой. Рост толщины пограничного слоя приводит к тому, что на некотором
расстоянии от входа пограничные слои смыкаются на оси трубы, условно разделяя
течение на так называемый начальный и основной участки (см. рис.22.4) с различным
видом профиля скорости. Разные профили скорости приводят и к разным законам
теплоотдачи. Рассмотрим теплоотдачу на основном участке при ламинарном режиме
течения (
кр
Re Re 〈 =2300) при q
w=
const.
Выделим в потоке кольцевой элемент (рис.22.4) и составим уравнение теплового баланса.
На координате R будем иметь:
dx
R
T
RQ
R
−=
∂
∂
πλ
2
&
, (a)
на
Q+dQ=QR+dR
RR+dR
&&&
:
, (b)
где dR
R
Q
QQd
R
∂
∂
&
&&
+= .
Вычитая (b) из (a) получим : dRdx
R
T
R2
R
Qd
=
∂
∂
λπ
∂
∂
&
. (n)
На координате x энтальпия потока
RdR2WTcI
xpx
πρ
=
&
,
на x+dx: dx
x
I
I=I+d I=I
xxx+dx
∂
∂
&
&&&&
+ , тогда
( )
dxRdRWTc
x
=Id
xp
πρ
∂
∂
2
&
. (e)
251
.
Так как тепловой поток, переданный за счет теплопроводности, идет на увеличение
энтальпии жидкости в выделенном элементарном объеме, то приравняем (n) и (e):
dRdx
x
T
R WcdRdx
R
T
R
R
xp
∂
∂
π
∂
∂
∂
∂
λπ
2
ρ
=2
,
=
x
T
R Wc
R
T
R
R
xp
∂
∂
λ∂
∂
∂
∂
ρ
.
При ламинарном режиме закон изменения скорости по радиусу находится по формуле:
( )
−
2
0
maxx
1=
R
R
WRW , тогда R
R
R
x
T
Wc
R
T
R
R
p
−⋅
=
2
0
max
1
ρ
∂
∂
λ∂
∂
∂
∂
, но при
q
w
=const сonst=
∂
∂
x
T
. Обозначим:
x
T
Wc
p
∂
∂
λ
max
ρ
=А, тогда
R
R
R
A
dR
dT
R
dR
d
=
2
0
-1 . (22.24)
Разделим переменные и проинтегрируем:
RdR
R
R
A
dR
dT
Rd
−=
2
0
1 ,
1
2
0
42
42
C
R
RR
A
dR
dT
R +
−= ,
R
C
R
RR
A
dR
dT
1
2
0
3
42
+
−= . (а)
Используем граничные условия для определения констант интегрирования:
при R=0 0
0
=
=R
dR
dT
⇒
⇒⇒
⇒
C
1
=0,
при R=R
0
0
4
1
0
AR
dR
dT
RR
=
=
. (*)
Рис.22.3
Рис.22.4
L
нач
/D≈0,03Re
