Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.

11
кгм
ккал
427
1
==
⇒
=
L
Q
AALQ , (2.2)
где
А
-
тепловой
эквивалент
работы
.
Таким
образом
,
Джоулем
было
доказано
,
что
определенной
затраченной
механической
работе
всегда
соответствует
выделение
определенного
количества
теплоты
.
Внутренняя
энергия
и
энтальпия
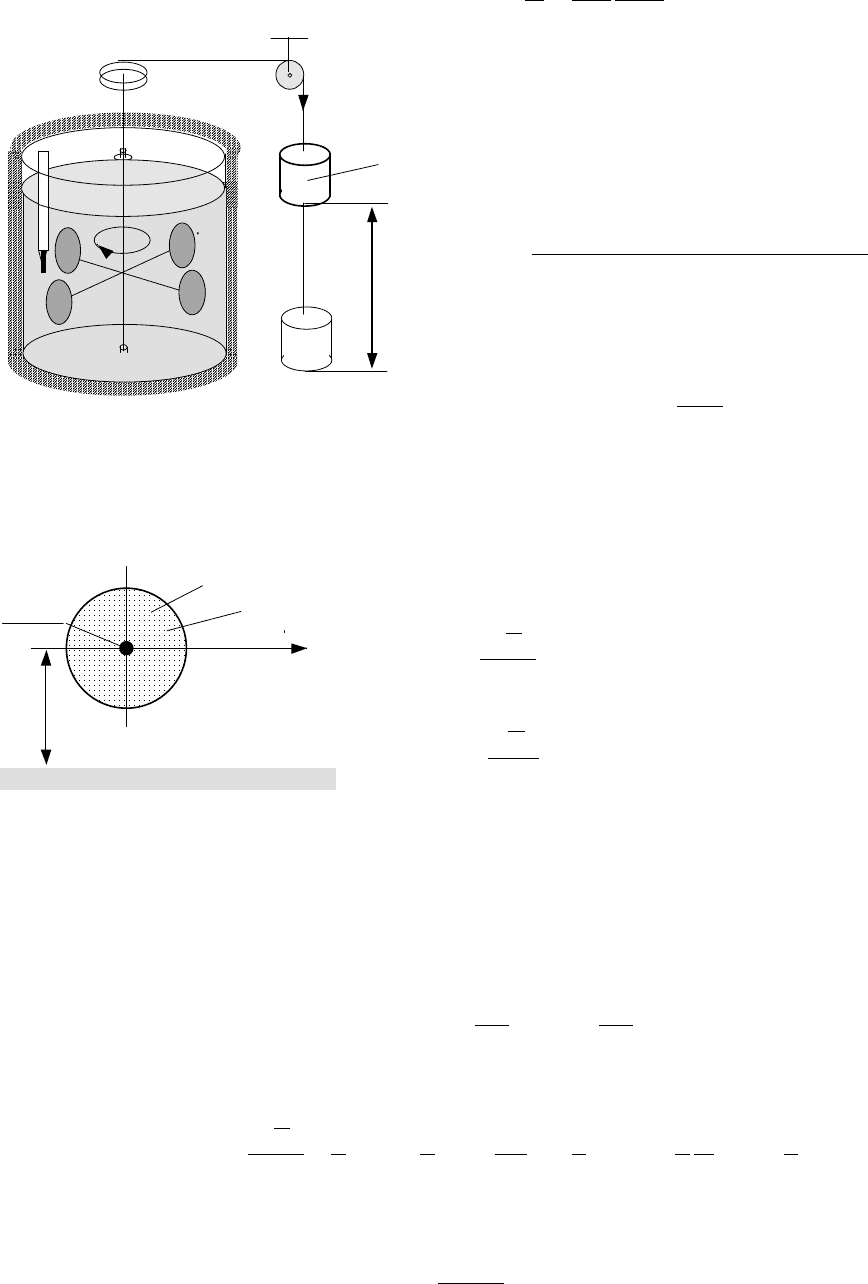
Энергия
движущегося
тела
Е
складывается
из
кинетической
Е
кин
,
потенциальной
Е
пот
и
внутренней
энергии
U
(
см
.
рис
.2.2),
т
.
е
.
UgGH
Gw
U
ЕЕЕ
++=++=
2
2
поткин
. (2.3)
В
дальнейшем
в
большинстве
случаев
будем
полагать
Е
кин
=
Е
пот
=0,
тогда
Е
=U.
В
свою
очередь
,
внутренняя
энергия
U
может
быть
представлена
в
виде
суммы
0
поткин
UUUU ++= , (2.4)
где
колвр
.
дп
.
дкин
UUUU ++= -
кинетическая
энергия
молекул
;
∑
=
=
n
i
ii
wm
U
1
2
П
.
Д
2
-
кинетическая
энергия
поступательного
движения
молекул
;
∑
=
=
n
i
ii
I
U
1
2
ВР
.
Д
2
ω
-
энергия
вращательного
движения
молекул
; I
i
,
ω
i
-
момент
инерции
и
угловая
скорость
молекулы
; U
кол
-
энергия
колебательного
движения
ядер
атомов
;
U
пот
-
потенциальная
энергия
взаимодействия
всех
молекул
между
собой
; U
0
-
внутренняя
энергия
тела
при
температуре
абсолютного
нуля
.
Внутренняя
энергия
реального
газа
U=f(T,V)
является
функцией
состояния
,
а
дифференциал
от
этой
функции
-
полным
:
dV
V
U
dT
T
U
dU
TV
∂
∂
+
∂
∂
=
. (2.5)
Для
идеального
газа
,
в
котором
молекула
рассматривается
как
материальная
точка
(
имеет
только
три
степени
свободы
поступательного
движения
)
GRTTR
G
TMRT
N
R
MNNkT
wm
NU
ii
2
3
2
3
2
3
2
3
2
3
2
00
0
0
0
2
ид
.
г
======
µ
, (2.6)
где
N –
число
молекул
.
В
общем
случае
GRTU
2
3
вр
ид
.
г
δ
+
= ,
Дж
, (2.7)
где
δ
вр
-
число
степеней
свободы
вращательного
движения
молекулы
.
Разделив
(2.7)
на
массу
газа
,
получим
удельную
внутреннюю
энергию
∆
Н
G
г
Рис
.2.1
t
Рис.2.2
U
газ
ц.т.
H
w
12
кг
Дж
,
2
3
вр
ид
.
г
RTu
δ
+
=
. (2.8)
Энтальпия, как и внутренняя энергия, является функцией состояния. По
определению энтальпия равна сумме внутренней энергии тела и потенциальной энергии
давления
I = U + pV .
(2.9)
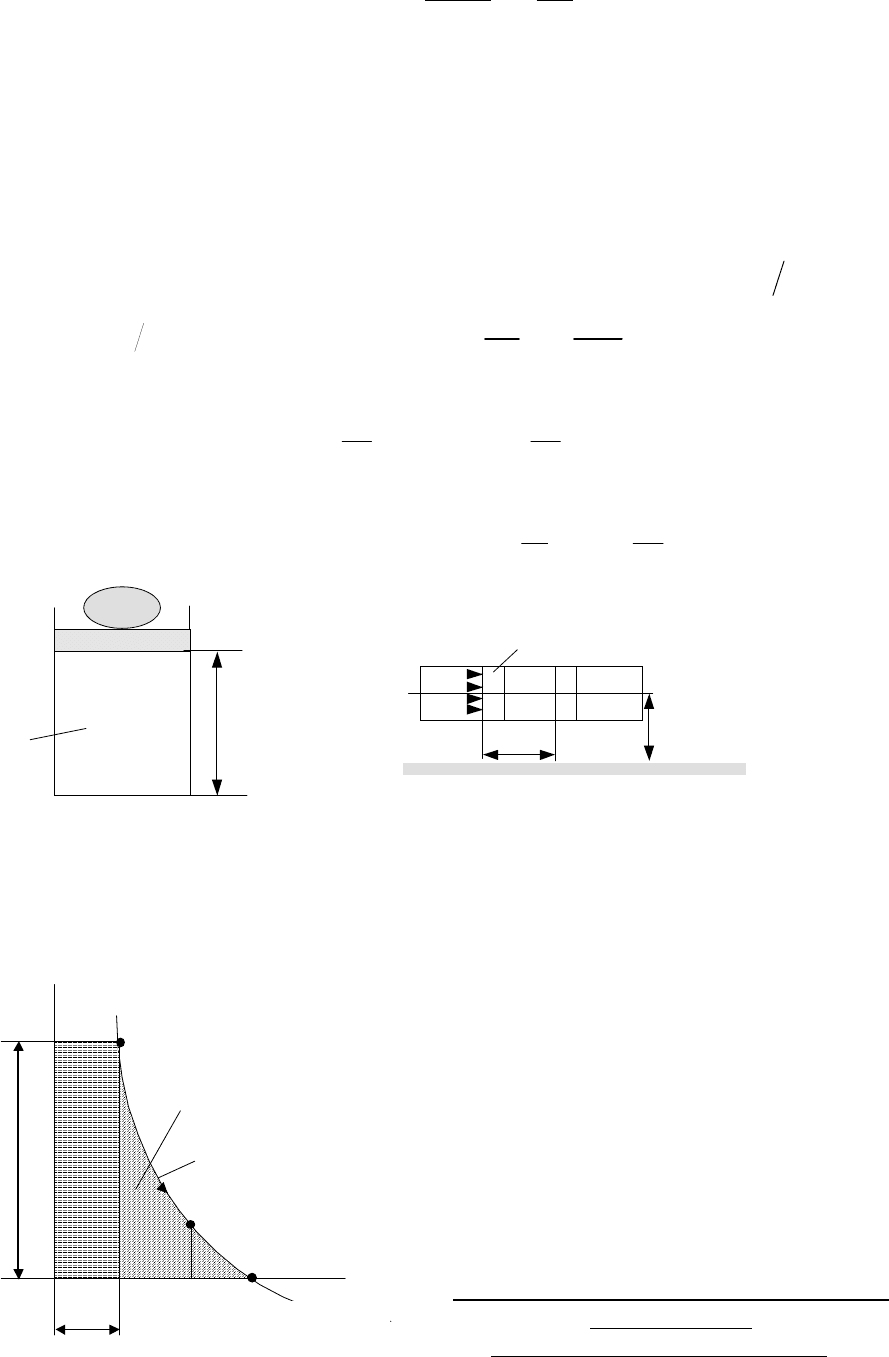
Действительно, если рассмотреть систему, состоящую из газа в цилиндре и поршня
площадью
F
с грузом, то
GgH = pFH = pV
. Таким образом, энтальпия характеризует
энергию расширенной системы. Рассмотрим открытую ТС. Сила статического
давления, действующая на элементарную массу
dG
, совершает работу проталкивания
pFdx
, перемещая этот элемент на расстояние
dx
, но
τ
wd
dx
=
, а
(
)
FGw
ρ
&
=
, кроме
того,
τ
ddGG =
&
, тогда
pvdGd
d
pdG
d
F
G
pFpFwdpFdx ====
τ
ρ
τ
ρ
τ
ф
&
.
Следовательно
,
для
открытой
системы
энергия
потока
элементарной
массы
равна
( )
dGghidGgh
w
idGgh
w
pvudE +=
++=
+++=
*
22
22
. (2.10)
Аналогично
внутренней
энергии
,
можно
записать
),(
TpfI
=
,
dT
T
I
dp
p
I
dI
p
T
∂
∂
+
∂
∂
=
. (2.11)
Внутренняя
энергия
U
и
энтальпия
I обладают
свойством
аддитивности
если
можно
пренебречь
поверхностной
энергией
на
границах
подсистем
,
что
справедливо
для
макротел
,
т
.
е
.
∑∑
==
==
n
i
i
n
i
i
IIUU
11
,
.
Внутреннюю
энергию
и
энтальпию
можно
показать
в
p-V диаграмме
(
см
.
рис
.2.5).
При
dS=
0
работа
изменения
объема
2121
UUL −=
−
.
Предположим
,
что
процесс
расширения
осуществляется
до
р
2
=0,
тогда
внутренняя
энергия
газа
в
точке
1
U
1
в
p-V
диаграмме
изобразится
площадью
1-
a-b-
1.
Так
как
1111
VpUI += ,
то
в
p-V диаграмме
энтальпия
определится
площадью
0-
c-
1
-
a-
0.
Аналитическое
выражение
первого
закона
термодинамики
для
закрытой
и
открытой
систем
Рассмотрим
закрытую
термодинамическую
систему
с
подвижной
PF
dG
dx
h
Рис
.2.4
↑
↑
↑
G
P
V
H
Рис.2.3
р
р
1
1
2
0
b
dS=
0
U
1
a
V
V
1
c
Рис
. 2.5
13
границей
и
начальными
параметрами
V
1
,
U
1
.
Если
внешняя
среда
совершит
работу
над
ТС
и
отдаст
ей
теплоту
,
то
внутренняя
энергия
в
новом
состоянии
равна
2112
2
1
−
+−=
∫
QpdVUU
V
V
, (2.12)
или
∫
+−=
−
2
1
1221
V
V
pdVUUQ
. (2.13)
Выражение
(2.13)
является
записью
первого
закона
термодинамики
для
закрытой
ТС
в
интегральной
форме
.
В
дифференциальном
виде
будем
иметь
:
pdVdUdQ
+
=
, (2.14)
т
.
е
.
теплота
,
подведенная
к
термодинамической
системе
,
в
общем
случае
идет
на
увеличение
внутренней
энергии
ТС
и
совершение
работы
изменения
объема
.
Для
более
сложных
закрытых
ТС
первый
закон
термодинамики
в
дифференциальной
форме
записывается
с
учетом
суммы
работ
∑
=
n
i
i
v
dL
1
,
не
связанных
с
изменением
объема
(
например
,
работа
против
сил
поверхностного
натяжения
,
работа
в
гравитационных
,
электрических
и
магнитных
полях
):
∑
=
++=
n
i
i
v
dLpdVdUdQ
1
.
Разделив
(2.14)
на
массу
газа
,
получим
pdvdudq
+
=
,
Дж
/
кг
. (2.15)
В
дальнейшем
,
как
правило
,
мы
будем
использовать
первый
закон
термодинамики
в
виде
(2.13)- (2.15).
Выполнив
преобразование
Лежандра
(
преобразование
меняет
местами
зависимые
и
независимые
переменные
)
над
(2.15),
т
.
е
.
прибавляя
и
вычитая
d(pv)
,
получим
другое
полезное
выражение
первого
закона
термодинамики
vdpdipdvvdppdvpvudpdvpvdpvddudq
−
=
+
−
−
+
=
+
−
+
=
)()()( . (2.16)
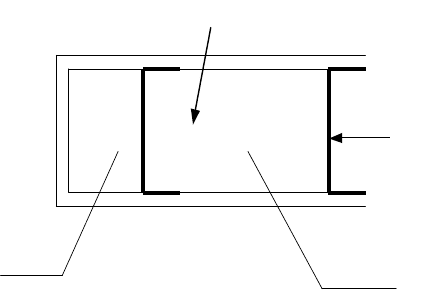
Рассмотрим
открытую
ТС
(
см
.
рис
.2.7).
На
входе
в
канал
,
расположенный
под
углом
к
горизонту
,
поток
имеет
энергию
1
*
11
gHGIE
&
&&
+=
,
а
на
выходе
:
2
*
22
gHGIE
&
&&
+=
.
В
результате
подвода
к
ТС
потока
теплоты
и
совершения
ею
технической
работы
в
единицу
времени
произойдет
изменение
энергии
потока
21тех2112 −−
−=− LQEE
&
&
&&
или
21тех211
*
12
*
2 −−
+=−−+ LQgHGIgHGI
&
&&
&
&
&
.
Разрешая
уравнение
относительно
потока
теплоты
,
получим
выражение
первого
закона
термодинамики
для
открытой
системы
в
интегральном
виде
)(
1221тех
*
1
*
221
HHgGLIIQ −++−=
−−
&
&&&
&
. (2.17)
В
дифференциальной
форме
будем
иметь
gdHGLdIdQd
&
&&
&
++=
тех
*
,
Вт
. (2.18)
В
большинстве
случаев
,
когда
в
качестве
рабочего
тела
используются
газы
или
пары
,
можно
положить
dH
=
0, тогда
U
1
,
V
1
U
2
,
V
2
pF
Q
1-2
Рис.2.6

14
тех
*
LdIdQd
&&
&
+=
. (2.19)
Рассмотрим
частные
случаи
.
Для
паровой
или
газовой
турбины
,
имеющей
тепловую
изоляцию
,
из
(2.19)
получим
*
тех
IdLd
&&
−= или
(
)
*
2
*
1
*
1
*
221тех
IIIIL
&&&&&
−=−−=
−
,
т
.
е
.
работа
турбины
(
техническая
работа
)
осуществляется
за
счет
убыли
полной
энтальпии
+==
2
2
**
c
iGiGI
&&
&
,
где
с-
скорость
потока
в
абсолютном
движении
.
Для
газа
,
движущегося
в
адиабатическом
канале
,
уравнение
энергии
примет
вид
0
*
=Id
&
,
или
=
*
I
&
const.
Таким
образом
,
для
любых
двух
сечений
при
постоянном
расходе
G
&
можно
написать
2
2
2
2
2
2
1
1
c
i
c
i +=+
.
Такая
запись
справедлива
как
для
идеального
,
так
и
для
реального
потока
с
трением
.
Действительно
,
работа
сил
трения
приводит
к
росту
удельной
энтальпии
и
уменьшению
скорости
,
но
всегда
const
2
2
*
=+=
c
ii
.
Первый
закон
термодинамики
для
открытой
ТС
справедлив
и
для
систем
,
в
которых
отсутствуют
тепловые
эффекты
.
Так
,
мощность
гидравлической
турбины
,
где
можно
считать
температуру
жидкости
практически
постоянной
,
равна
(
)
1221
тех
HHgGL −−=
−
&
&
.
Из
приведенных
примеров
видно
,
что
первый
закон
термодинамики
является
универсальным
законом
природы
.
Первый
закон
термодинамики
с
учетом
переменной
массы
Примерами
термодинамической
системы
с
переменной
массой
могут
служить
процесс
закачки
газа
в
емкость
,
процесс
расширения
газа
в
двигателе
внутреннего
сгорания
при
наличии
утечек
газа
из
цилиндра
в
окружающую
среду
,
и
т
.
п
.
В
первом
случае
(
рис
.2.8
а
)
будем
иметь
∫
+−=
−
G
idGQUU
0
2112
. (2.20)
Для
второго
случая
можно
написать
VpdUdGidQd
&&
&&
+=+
,
(2.21)
здесь
0
<
G
d
&
,
в
общем
случае
G
d
&
может
принимать
как
отрицательные
,
так
и
положительные
значения
.
21−
Q
&
1
2
Рис.2.7
H
1
1
Е
&
2
Е
&
21тех −
L
&
H
2
dG
.
Q
1-2
T>T
ос
а
б
Рис
. 2.8

15
Применение
первого
закона
термодинамики
к
круговому
процессу
Под
круговым
процессом
,
или
циклом
,
понимают
совокупность
последовательных
процессов
,
в
результате
совершения
которых
ТС
возвращается
в
исходное
состояние
.
В
технике
используют
как
прямые
циклы
,
когда
в
p-v диаграмме
кривая
расширения
А
-
а-В
лежит
выше
кривой
сжатия
В
-
b-
A (
рис
.2.9),
так
и
обратные
,
где
процесс
расширения
лежит
ниже
процесса
сжатия
.
Все
тепловые
машины
работают
по
прямому
циклу
,
а
холодильные
-
по
обратному
.
Проведя
идеальные
адиабаты
(
изоэнтропы
ds=
0)
через
точки
А
и
В
цикла
,
разобьем
его
на
две
части
:
процесс
А-а-В
,
где
к
рабочему
телу
подводится
теплота
q
I
и
процесс
В-b-А
,
где
осуществляется
отвод
теплоты
q
II
.
Проинтегрируем
уравнение
,
описывающее
первый
закон
термодинамики
,
по
замкнутому
контуру
∫
∫
∫
+= dldudq . (2.22)
Так
как
при
возвращении
рабочего
тела
в
круговом
процессе
в
исходное
состояние
∫
= 0du
,
то
q
ц
= l
ц
,
т
.
е
.
работа
цикла
равна
теплоте
цикла
.
Так
как
q
ц
= q
I
- q
II
,
то
III
ц
qql −= . (2.23)
Количественную
сторону
превращения
в
работу
подведенной
в
идеальном
цикле
теплоты
характеризует
термический
КПД
цикла
I
II
I
III
I
ц
1
q
q
q
qq
q
l
t
−=
−
==
η
, (2.24)
который
представляет
собой
отношение
идеальной
работы
цикла
к
теплоте
,
подведенной
в
этом
цикле
.
Так
как
согласно
второму
закону
термодинамики
невозможно
достичь
абсолютного
нуля
температуры
,
то
q
II
всегда
больше
нуля
и
,
следовательно
,
t
η
всегда
меньше
единицы
.
3.
Приложение первого закона термодинамики
к идеальным газам
Свойства
идеального
газа
.
Опыты
Гей
-
Люссака
,
Бойля
и
Мариотта
.
Термическое
уравнение
состояния
Под
идеальным
газом
(
ИГ
),
как
отмечалось
выше
,
понимают
такой
газ
,
молекулы
которого
рассматриваются
как
материальные
точки
,
имеющие
массу
,
но
не
имеющие
объема
.
Взаимодействие
между
молекулами
ИГ
осуществляется
только
за
счет
упругих
соударений
,
силы
взаимного
притяжения
и
отталкивания
между
молекулами
отсутствуют
.
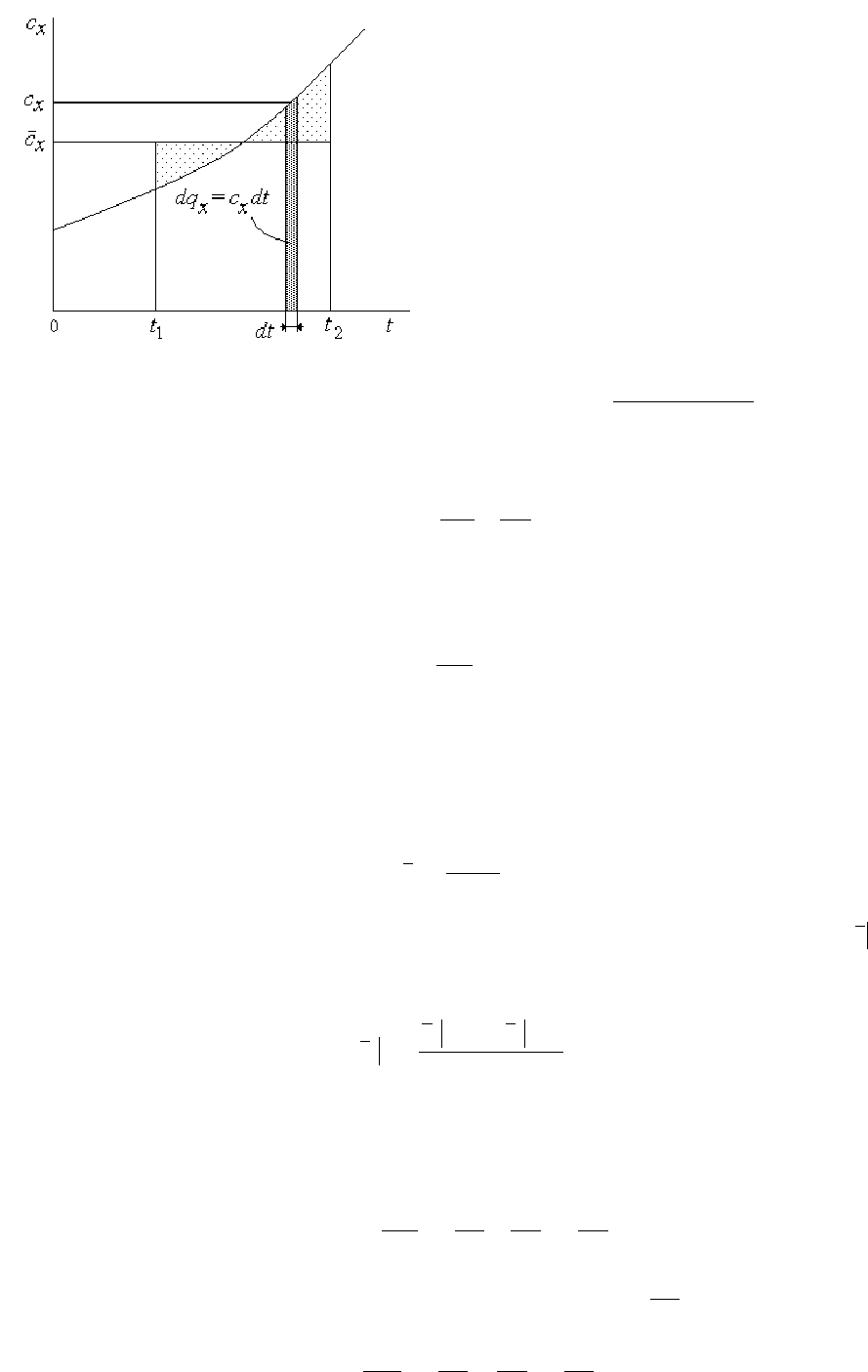
В
1806
г
.
Гей
-
Люссак
проводит
опыт
с
целью
определения
зависимости
внутренней
энергии
газа
от
объема
.
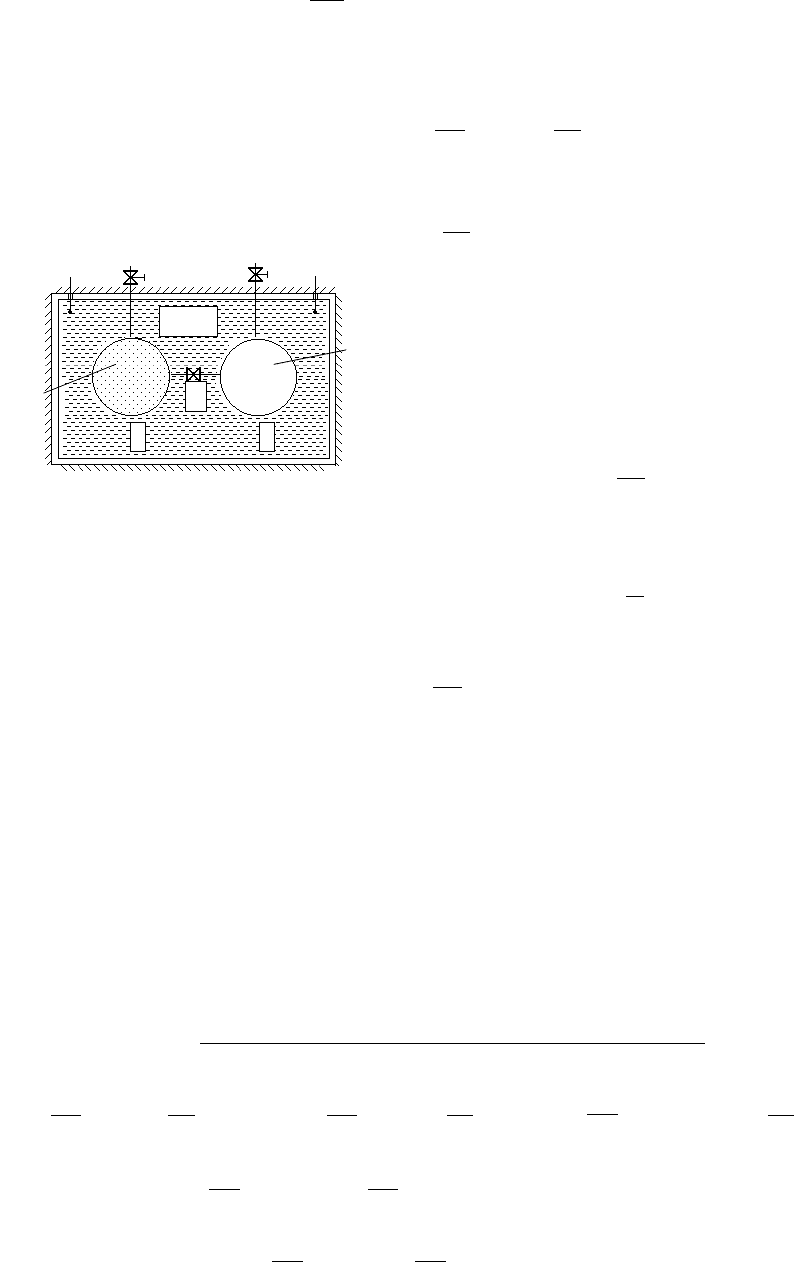
В
сосуде
1 (
рис
.3.1)
находился
газ
под
небольшим
давлением
р
1
,
чтобы
ослабить
силы
взаимного
притяжения
между
молекулами
,
в
сосуде
2 -
р
2
≈0.
Вся
система
была
теплоизолирована
,
работа
внешних
сил
отсутствовала
,
т
.
е
.
внутренняя
энергия
не
могла
измениться
,
0=
∂
∂
+
∂
∂
= dV
V
U
dT
T
U
dU
TV
. (3.1)
После
открытия
крана
К
газ
заполнял
емкость
2,
при
этом
в
первый
момент
термометр
1
показал
некоторое
понижение
температуры
,
а
второй
-
повышение
,
однако
через
q
II
c
d
b
a
B
A
p
v
ds=0
ds=
0
l
ц
q
I
Рис.2.9
16
некоторое
время
,
после
установления
теплового
равновесия
в
термостате
,
термометры
стали
показывать
первоначальное
значение
.
Таким
образом
, dT=0,
но
теперь
газ
занимал
две
емкости
,
т
.
е
. dV
≠
0.
Выполнение
условия
(3.1)
требует
,
чтобы
0
=
∂
∂
T
V
U
.
На
основании
этого
опыта
Гей
-
Люссак
показал
,
что
внутренняя
энергия
разряженных
реальных
газов
(
р
≤ 3
МПа
)
не
зависит
от
объема
и
такие
газы
могут
рассматриваться
как
идеальные
(
см
.
ф
-
лу
1.9).
Для
энтальпии
будем
иметь
0
=
∂
∂
+
∂
∂
= dp
p
I
dT
T
I
dI
T
p
, но
dT=
0, a
dp≠
0,
откуда для идеального газа получаем
0
=
∂
∂
T
p
I
.
Бойль и Мариотт независимо друг от
друга установили, что при
T=
const
произведение
pv=
const, т.е.
(
)
Tfpv
=
. (а)
Разделив (а) на Т, получим новую функцию,
также зависящую от температуры:
( )
T
T
pv
ϕ
=
. (b)
Гей-Люссак установил, что при р
=
const
отношение
v/T=
const, следовательно,
( )
p
T
v
ψ
=
. (с)
Умножим (с) на р
и получим функцию
( )
pF
T
pv
=
. (d)
Сравнивая (b) и (d), приходим к выводу, что в правой части уравнений должна быть
константа, независящая от Т
и р. Эта константа называется газовой постоянной
R
, так что
можно написать
RTpv
=
. (3.2)
Уравнение (3.2) является термическим уравнением состояния идеального газа в форме
Клапейрона. Умножая (3.2) на массу газа, получим
GRTpV
=
, (3.3)
где
R=R
0
/
µ
. Так как
G=M
µ
, то (3.3) можно представить в форме Клапейрона-Менделеева
TMRpV
0
=
. (3.4)
Внутренняя энергия и энтальпия идеального газа
Для реального газа
u=f(T,v)
, а
i=
ϕ
(T,p)
, тогда
dp
p
i
dT
T
i
didv
v
u
dT
T
u
du
T
pTv
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
=
, , но
0=
∂
∂
T
v
u
0и
=
∂
∂
T
p
i
,
следовательно,
dT
T
i
didT
T
u
du
pv
∂
∂
=
∂
∂
=
, .
Ниже будет показано, что
v
v
с
T
u
=
∂
∂
, а
p
p
c
T
i
=
∂
∂
(см. ф-лы 3.14 и 3.15). Таким образом,
для идеального газа справедливы выражения
t
2
t
1
1
2
вода
р
1
р
2
=0
Рис.3.1
K
17
dTcdu
v
=
,
(3.5)
dTcdi
p
=
,
(3.6)
где
pv
с
c
и - удельные изохорная и
изобарная теплоемкости, Дж/(кг
⋅
К). В
интегральной форме будем иметь
(
)
121221
TTcuuu
v
−=−=∆
−
,
(3.7)
(
)
121221
TTciii
p
−=−=∆
−
.
(3.8)
Теплоемкость
Под истинной теплоемкостью понимают предел отношения бесконечно малого
количества теплоты, подведенного к телу, к вызванному этим подводом изменению
температуры тела при
∆
Т
→
0
dT
dQ
T
Q
C
T
=
∆
∆
=
→∆
lim
0
, Дж/К. (3.9)
Так как
dQ
зависит от характера процесса, то и теплоемкость является функцией процесса.
Теплоемкость может изменяться от -
∞
до +
∞
. Разделив (3.9) на массу тела, получим
удельную истинную теплоемкость
dT
dq
c
x
x
=
, Дж/(кг
⋅
К). (3.10)
Теплоемкость реальных газов зависит от температуры и может быть аппроксимирована
полиномом
...
2
+++= dtbtac
. (3.11)
Кроме истинной теплоемкости используют понятие средней теплоемкости в заданном
интервале температур (см. рис.3.2)
∫
−
=
2
1
)(
1
12
t
t
xx
dttc
tt
c
. (3.12)
Если в термодинамических таблицах приводятся средние значения теплоемкости
t
c
0
в
интервале от 0 до
t
, то значение средней теплоемкости в заданном интервале находится из
формулы
12
1
0
2
0
12
2
1
tt
tctc
c
t
x
t
x
t
t
x
−
⋅−⋅
=
. (3.13)
Чаще всего в термодинамических расчетах используют удельные изохорную и
изобарную теплоемкости.
Первый закон термодинамики
dq=du+pdv
для изохорного процесса (
dv=
0)
принимает вид
dq
v
=du
, тогда
vv
v
v
T
u
dT
dT
T
u
dT
dq
c
∂
∂
=
∂
∂
==
. (3.14)
Для изобарного процесса (
dp=
0) будем иметь
dT
T
i
didq
p
p
∂
∂
==
, следовательно,
pp
p
p
T
i
dT
dT
T
i
dT
dq
c
∂
∂
=
∂
∂
==
. (3.15)
Рис. 3.2
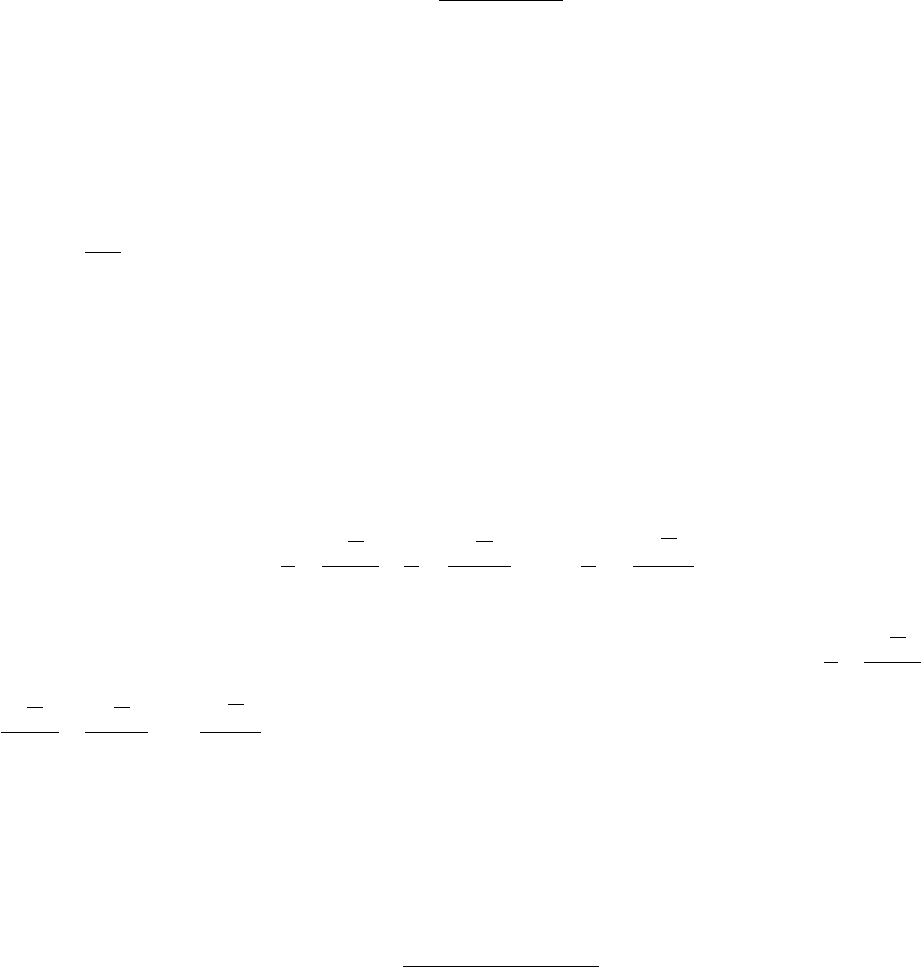
18
Найдем связь между изохорной и изобарной теплоемкостями. Продифференцируем
выражение энтальпии
i=u+pv
:
(
)
pvddudi
+
=
, но для идеального газа
(
)
RdTpvd
=
,
тогда
RdTdTcdTc
vp
+=
, или
Rcc
vp
=−
. (3.16)
Выражение (3.16) называется формулой Майера. Так как
R -
величина положительная, то
изобарная удельная теплоемкость газа всегда больше изохорной.
Смеси газов
В большинстве энергетических систем и машин в качестве рабочего тела
применяются механические смеси газов. Поэтому необходимо рассмотреть основные
свойства газовых смесей. Составляющие газовой смеси называются компонентами. Так
как масса обладает свойством аддитивности, то можно написать
n
GGGG +++=
...
21
см
.
Разделив левую и правую части на массу смеси, получим
∑
=
=
n
i
i
g
1
1
, (3.17)
где
см
G
G
g
i
i
=
- массовая доля
i
-го компонента.
Согласно закону Дальтона, давление смеси идеальных газов равно сумме
парциальных давлений ее компонентов
∑
=
=
n
i
i
pp
1
см
. (3.18)
Под парциальным давлением
p
i
понимают давление, которое имел бы
i
-й газ,
занимая весь объем смеси при температуре смеси. Отметим, что закон Дальтона
справедлив только для смеси идеальных газов, так как только в этом случае можно
написать (см. модель идеального газа)
2
3
2
....
2
3
2
2
3
2
2
см
2
22
2
2
11
1
см
wm
с
wm
с
wm
с
p
=++=
,
где с
см
= с
1
+ с
2
+...+ с
n
- концентрация смеси (количество молекул в единице объема
смеси), равная сумме концентраций всех ее компонентов;
2
3
2
2
ii
ii
wm
с
p =
;
2
....
2
2
2
2
22
2
11
wm
wmwm
==
при Т=соnst.
Получим выражение для газовой постоянной смеси. Запишем уравнения состояния
для компонентов смеси через парциальные давления и сложим их:
смсм
см
22
см
2
см
11
см
1
.....
TRGVp
TRGVp
TRGVp
nnn
=
+
=
+
=
+
i
n
i
i
n
i
i
RGTpV
∑∑
==
=
1
см
1
см
. (а)
С учетом (3.18) получим
i
n
i
i
RGTpV
∑
=
=
1
смсмсм
. (b)
Для всей смеси можно записать
смсмсмсмсм
RGTpV =
. (с)
Сравнивая (b) и (с), приходим к выводу, что

19
i
n
i
i
RGTRGT
∑
=
=
1
смсмсмсм
. (d)
Разделив (d) на массу смеси, получим
∑
=
=
n
i
ii
RgR
1
см
. (3.19)
Представим уравнение состояния для
i
-го компонента через парциальное давление
p
i
и
приведенный (парциальный) объем
V
i
:
смсм
TRGVp
iii
=
, (е)
смсм
TRGVp
iii
=
, (f)
откуда следует, что
ii
VpVp
смсм
=
. (g)
Суммирование (g) по индексу
i
дает
∑
=
=
n
i
i
VV
1
см
, (3.20)
под приведенным (парциальным) объемом
i
-ого компонента понимают объем, который
занимал бы
i
-й газ при температуре и давлении смеси. Отношение
см
/VVr
i
i
=
называется объемной долей
i
-ого компонента. Разделив (3.20) на объем смеси, получим
1
1
=
∑
=
n
i
i
r
. (3.21)
Используя (g), можно написать
1
см
см
см
==
i
ii
i
r
p
p
Vp
Vp
, откуда
ii
rpp
см
=
. (3.22)
Разделив (f) на (с), найдем связь между объемными и массовыми долями компонентов
i
i
i
ii
g
R
R
gr
µ
µ
см
см
==
, (3.23)
так как
i
i
RR
µ
0
=
, где
µ
i
-
молекулярная масса.
Записав (3.23) в виде
i
i
i
rg
µ
µ
=
см
, после суммирования по
i
определим кажущуюся
молекулярную массу смеси
∑∑
==
=
n
i
ii
n
i
i
rg
11
см
µµ
, но
1
1
=
∑
=
n
i
i
g
, тогда
∑
=
=
n
i
ii
r
1
см
µµ
. (3.24)
Так как
G=M
µ
, где
М
- число киломолей, то
∑∑
===
i
i
i
i
i
i
gG
G
M
G
µµ
µ
1
см
см
см
см
. (3.25)
С другой стороны,
∑
∑
===
i
ii
i
ii
N
M
M
M
G
µ
µ
µ
смсм
см
см
, (3.26)
где
см
MMN
ii
= - мольная доля i-го компонента.
Из сравнения (3.24) и (3.26) следует, что
i
i
Nr
=
, (3.27)
т.е. объемные и мольные доли численно равны.
Определим плотность смеси
20
∑∑
===
i
ii
i
ii
rV
VV
G
ρρρ
смсм
см
см
1
, (3.28)
где
см
см
TR
p
V
G
ii
i
i
==
ρ
. Введем понятие парциальной плотности
см
V
G
i
i
=
′
ρ
. Суммирование по i
дает
см
см
1
ρρ
==
′
∑∑
i
i
i
i
G
V
, т.е. плотность смеси равна сумме парциальных
плотностей компонентов
∑
′
=
i
i
ρρ
см
,
(3.29)
где
см
TR
p
i
i
i
=
′
ρ
.
Теплоемкость смеси
Если пренебречь поверхностной энергией на границах раздела компонентов, то
можно написать
∑
∑
∆=∆=∆=∆
i
i
v
i
iv
GcTUTGcU
смсмсм
см
см
. (3.30)
Разделив (3.30) на G
см
, получим
∑
=
i
iviv
gcc
см
.
(3.31)
Аналогичные преобразования с выражением для энтальпии
∑
∆=∆
i
i
II
см
(3.32)
приводят к формуле
∑
=
i
ipip
gcc
см
. (3.33)
Отметим, что при определении массовой теплоемкости смеси (Дж/(кгК))
теплоемкости компонентов умножаются на их массовые доли. При расчете теплоемкости
с размерностью Дж/(нм
3
К) применяются формулы с объемными или мольными долями:
∑
∑
′
=
′
=
′
i
ivi
i
iviv
Ncrcc
см
, (3.34)
∑
∑
′
=
′
=
′
i
ipi
i
ipip
Ncrcc
см
. (3.35)
Для мольных теплоемкостей (Дж/(кмольК)) имеем, соответственно
∑
∑
==
i
iiv
i
iivv
Ncrcc
µµµ
см
, (3.36)
∑
∑
==
i
iip
i
iipp
Ncrcc
µµµ
см
. (3.37)
Переход от теплоемкостей с одной размерности на другую осуществляется делением или
умножением на
µ
,
ρ
, v, например,
н
ρ
v
v
cc
=
′
.
Приведенные формулы справедливы как для истинных, так и для средних
теплоемкостей в заданном интервале температур.
