Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.

21
Основные виды процессов
Любой цикл тепловой или холодильной машины состоит из совокупности
отдельных последовательных термодинамических процессов. Рассмотрим их.
Изохорический процесс, dv=0 - процесс, протекающий при постоянном объеме. Полагая
v=const в уравнении состояния pv=RT , полу
чим уравнение процесса
const=
T
p
. (3.38)
Используя (3.38), найдем связь между параметрами на кривой процесса в точках 1 и 2
2
2
1
1
T
p
T
p
= . (3.39)
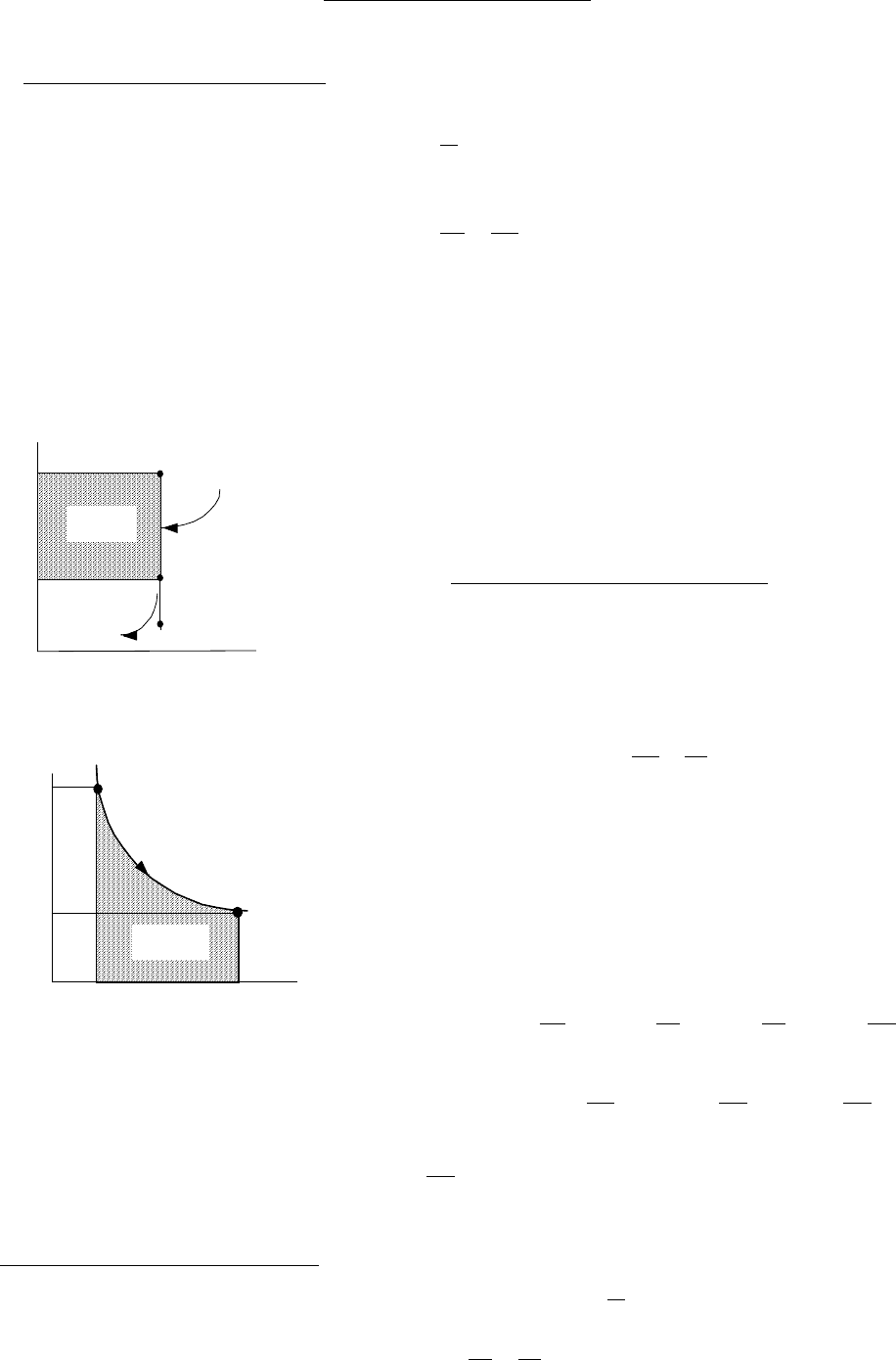
Изображение процесса в p-v диаграмме представлено на рис.3.3. Из первого закона
термодинамики dq=du+pdv получим
dq = du , (3.40)
или в интегральной форме
1221
uuq −=
−
, (3.41)
т.е. в изохорном процессе подведенная (процесс 1-2) или отведенная
(процесс 1-3) теплота идет на изменение внутренней
энергии газа. Так как dv=0, то работа изменения объема
равна нулю dl=pdv=0, а техническая - нет:
)(,0
122-
тех
1
тех
ppvlvdpdl −−=≠−= .
Изотермический процесс, dT=0
Используя уравнение состояния идеального газа pv=RT ,
получим уравнение процесса (равнобокая гипербола в p-v
координатах)
pv=const. (3.42)
Из (3.42) найдем связь между параметрами
1
2
2
1
v
v
p
p
= . (3.43)
Так как dT=0, то du = c
v
dT = 0, тогда из dq=du+pdv
следует, что в изотермическом процессе подведенная
или отведенная теплота численно равна работе
изменения объема, т.е.
dq = pdv.
(3.44)
Работа изменения объема в изотермическом процессе
равна технической работе
(3.45).ln
lnln
,lnlnln
2
1
1
2
1
2
111121тех
2
1
1
2
1
2
111121
2
1
2
1
2
1
2
1
p
p
RT
p
p
RT
p
p
vp
p
dp
vpvdpl
p
p
RT
v
v
RT
v
v
vp
v
dv
vppdvl
p
p
p
p
v
v
v
v
=
−=−=−=−=
=====
∫ ∫
∫ ∫
−
−
Изобарический процесс, d
р
=0. При p=const из уравнения состояния pv=RT получим
уравнение процесса const=
T
v
, (3.46)
Откуда следует
2
1
2
1
T
T
v
v
= .
(3.47)
-l
тех1-2
q
1
-
2
q
1-3
p
v
2
1
3
Рис.3.3
Рис.3.4
v
2
l
1
-
2
v
v
1
p
1
p
2
p
1
2

22
Из первого закона термодинамики dq = di - vdp при
р
=const будем иметь
dq = di , (3.48)
или
1221
iiq −=
−
. (3.49)
Работа изменения объема равна
( )
1221
2
1
vvppdvl
v
v
−==
∫
−
. (3.50)
Так как dp=0 , то техническая работа
изобарического процесса равна нулю.
Изоэнтропийный процесс, ds=0 (идеальный
адиабатический процесс). Из объединенного
закона термодинамики (первого и второго) для
обратимого изоэнтропийного процесса можно
написать 0
=
+
=
=
pdvduTdsdq .
(3.51)
Так как dl = pdv , то dTcdudl
v
−=−= ,
(3.52)
или в интегральной форме
(
)
(
)
121221
TTcuul
v
−−=−−=
−
, (3.53)
т.е. работа изменения объема осуществляется за счет убыли внутренней энергии.
Для технической работы из первого закона термодинамики
dq = di - vdp = 0 получим
dTcdidl
p
−=−=
тех
. (3.54)
В интегральной форме будем иметь
(
)
(
)
121221тех
TTciil
p
−−=−−=
−
. (3.55)
Получим уравнение процесса. Имеем:
0или,0 =+=+ pdvdTcpdvdu
v
. (а)
Продифференцируем уравнение состояния pdv + vdp = RdT и подставим dT в (а):
(
)
0 или0 =++=++ vdpcpdvR
с
Rpdvvdpcpdvc
vvvv
. (b)
После деления (b) на
v
c
с учетом, что
pv
cRc
=
+
получим уравнение идеальной
адиабаты (изоэнтропы) в дифференциальной форме
0=+
p
dp
v
dv
k , (3.56)
где
vp
cck = - показатель изоэнтропы для идеального газа. В интегральной форме будем
иметь const=
k
pv (3.57)
(формула получена Пуассоном в 1823 г).
В общем случае для изоэнтропийного процесса реального
газа, разделив (2.16) на (2.15), можно получить выражение
показателя изоэнтропы
ss
v
p
p
v
u
i
k
∂
∂
−=
∂
∂
= . Из (3.56)
найдем, что
v
p
k
v
p
s
−=
∂
∂
, (3.58)
а из (3.42) после дифференцирования получим
v
p
v
p
T
−=
∂
∂
, (3.59)
так как k>1, то
Ts
v
p
v
p
∂
∂
>
∂
∂
, то есть в p-v диаграмме
1 2
Т
1
Т
2
p
p
v
рис.3.5
l
1-2
1
2
s
2
т
р
1
р
2
р
v
ds=
0
dT=
0
Рис. 3.6
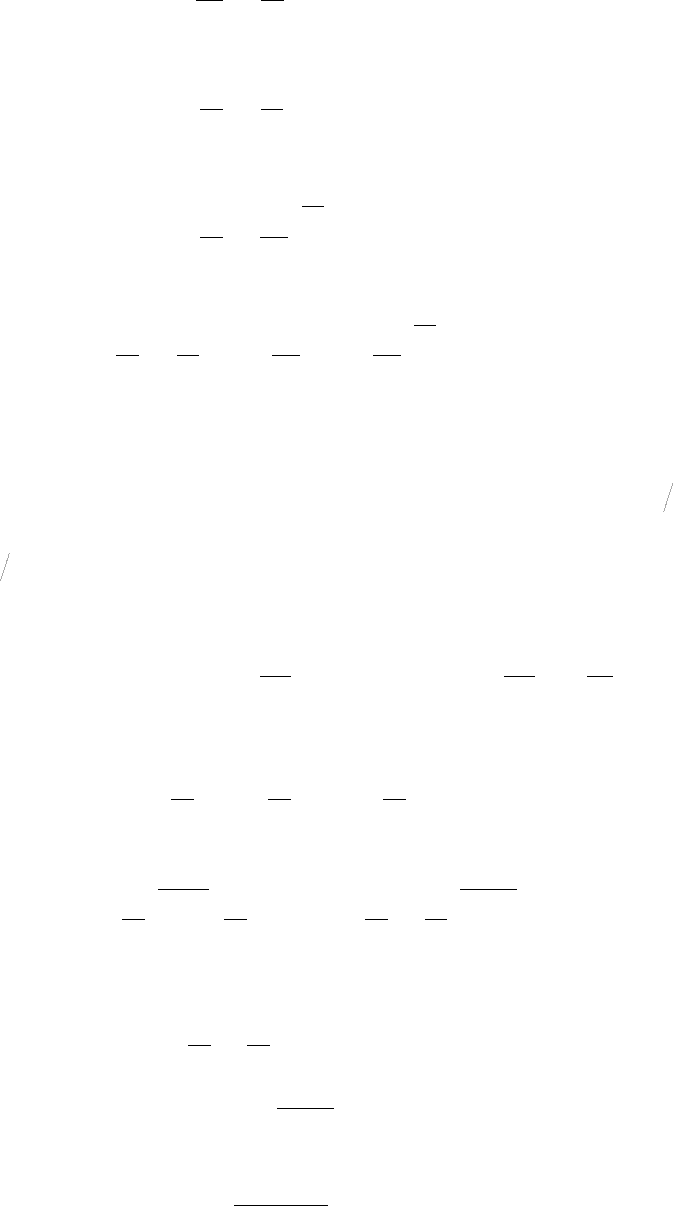
23
изоэнтропа идет круче изотермы (см. рис.3.6). Деление (3.54) на (3.52) показывает, что
техническая работа в изоэнтропном процессе больше работы изменения объема в k раз
kdldl =
тех
. (3.60)
Найдем связь между термодинамическими параметрами изоэнтропийного процесса.
Используя уравнение (3.57), можно написать
k
v
v
p
p
=
1
2
2
1
. (3.61)
Подставив выражение для давления
р
=RT/v
из уравнения состояния в (3.61), получим
1
1
2
2
1
−
=
k
v
v
T
T
. (3.62)
Подставляя в (3.62)
k
ppvv
/1
2112
)/()/(
=
, можно также получить
k
k
p
p
T
T
1
2
1
2
1
−
=
. (3.63)
Таким образом, справедливы равенства
k
k
kk
p
p
v
v
T
T
1
2
1
1
2
1
1
1
2
2
1
−
−−
=
=
=
ρ
ρ
. (3.64)
Если в качестве рабочего тела используется запыленный поток (поток идеального
газа, содержащий примесь в виде твердых микрочастиц или капель), то значение
показателя изоэнтропы изменяется и зависит от массового содержания частиц или влаги в
потоке. С увеличением загрузки потока твердыми частицами или каплями
гк
GGu
&&
=
показатель изоэнтропы смеси
k
cм
→
1, т.е. процесс приближается к изотермическому, если
u →
0, то
ггсм
vp
сс
kk =→
. Получим выражение для
см
k
.
Будем считать, что процесс теплообмена между потоками газа и капель (или
частиц) обратимый, тогда приращение энтропии системы (газ-капли) равно нулю
0
кгc
=+= SdSdSd
&&&
(а),
T
dT
cGSd
p
к
кк
&&
=
(b),
+=
v
dv
R
T
dT
cGSd
v г
г
гг
&&
. (c)
Так как процесс обратимый, то
Т
г
=
Т
к
=
Т
.
Подставляя (b) и (с) в (а), после интегрирования
получим
0lnlnln
1
2
к
1
2
г
1
2
г
=−+
T
T
uc
v
v
R
T
T
c
pv
. (d)
Разделив (d) на
R
г
, можно написать
0ln
1
2
1
2
г
кг
=
⋅
−
v
v
T
T
R
ucc
pv
, или
кг
г
2
1
1
2
pv
ucc
R
v
v
T
T
−
=
, (е)
но при изоэнтропийном процессе для чистого газа связь между параметрами имеет вид
1
2
1
1
2
−
=
k
v
v
T
T
. (f)
Сравнивая (е) и (f), приходим к выводу, что
1
см
кг
г
−=
−
k
ucc
R
pv
, откуда с учетом того, что
ггг vp
ccR −=
найдем выражение показателя изоэнтропы запыленного потока
кг
кг
см
р
v
рр
исс
исс
k
−
−
=
. (3.65)
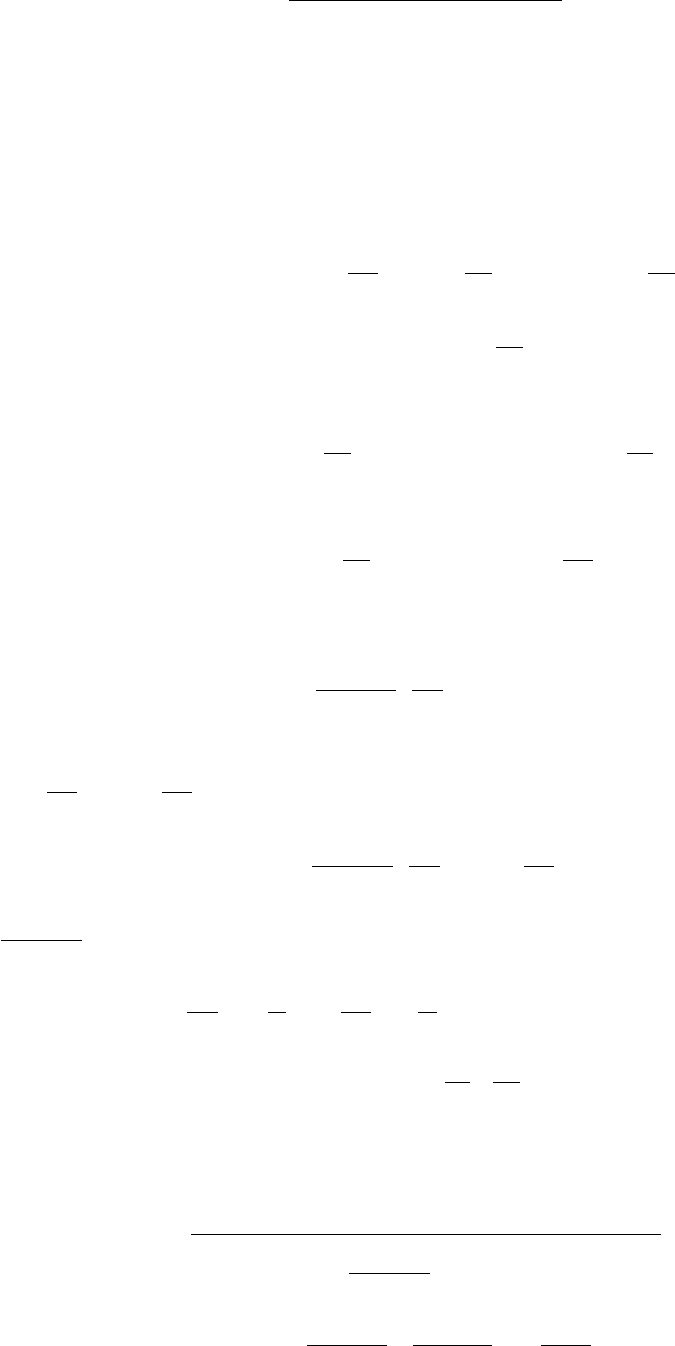
24
Политропический процесс
Процессы, протекающие в реальных энергетических машинах, как правило,
отличаются от рассмотренных выше, занимают некоторое промежуточное положение и
называются политропическими. Например, в двигателе внутреннего сгорания (ДВС) во
время рабочего хода отводится теплота и линия процесса в
p-v
диаграмме располагается
между изотермой и изоэнтропой. Процессы при
dT=
0,
dp=
0,
dv=
0,
ds=
0
являются
частными случаями более общего понятия “политропический процесс”.
Выведем уравнение политропического процесса. Подставим в уравнение первого
закона термодинамики
dq=du+pdv
значения
dTcdq
n
=
, где
n
c
- удельная теплоемкость
политропического процесса, и
dv
v
u
dTcdv
v
u
dT
T
u
du
T
v
Tv
∂
∂
+=
∂
∂
+
∂
∂
=
:
( )
0=
+
∂
∂
+− dvp
v
u
dTcc
T
nv
. (а)
Записывая первый закон термодинамики в двух формах
dpv
p
i
dTcdqdvp
v
u
dTcdq
T
p
T
v
−
∂
∂
+=
+
∂
∂
+= ,
и
приравнивая
правые
части
,
полагая
dp=0,
получим
( )
p
vp
T
v
T
ccp
v
u
∂
∂
−=
+
∂
∂
. (b)
Подставляя
(b)
в
(
а
),
приходим
к
уравнению
политропического
процесса
в
дифференциальной
форме
в
переменных
v
и
Т
:
(
)
( )
0=+
∂
∂
−
−
dTdv
v
T
cc
cc
pnv
vp
. (3.66)
Подставляя
выражение
дифференциала
температуры
как
функции
двух
переменных
v
и
р
dp
p
T
dv
v
T
dT
T
p
∂
∂
+
∂
∂
=
в
(3.66),
получим
(
)
( )
0=
∂
∂
+
∂
∂
−
−
dp
p
T
dv
v
T
cc
cc
v
pnv
np
, (3.67)
где
(
)
( )
n
cc
cc
nv
np
=
−
−
-
показатель
политропы
.
Для
идеального
газа
R
v
p
T
R
p
v
T
v
p
=
∂
∂
=
∂
∂
a, ,
тогда
(3.67)
примет
вид
0=+
p
dp
v
dv
n , (3.68)
или
в
интегральной
форме
const=
n
pv . (3.69)
Теплота
и
работа
политропического
процесса
Выразим
n
с
из
равенства
(
)
( )
nv
np
cc
cc
n
−
−
= :
1
1
1
−
−
=
−
−
=
−
−
=
n
kn
c
n
cnc
n
ncc
c
v
pvvp
n
. (3.70)
Теперь
элементарную
теплоту
политропического
процесса
можно
представить
в
виде

25
dT
n
kn
cdq
v
−
−
=
1
. (3.71)
Интегрируя
(3.71),
получим
( )
1221
1
TT
n
kn
cq
v
−
−
−
=
−
.
(3.72)
Для
элементарной
работы
изменения
объема
можно
написать
( )
.
1
1
1111
pvd
n
dT
n
R
dT
n
cc
dT
n
kcc
dTc
n
kcnc
dudqdl
pv
vv
v
vv
−
−=
−
−=
−
−
=
−
−
=
−
−
−
=−=
(3.73)
В
интегральном
виде
( ) ( )
11221221
1
1
1
vpvp
n
TT
n
R
l −
−
−=−
−
−=
−
. (3.74)
Элементарная
техническая
работа
( )
.
111
тех
pvd
n
n
RdT
n
n
dTc
n
kn
cdidqdl
pv
−
−=
−
−=
−
−
−
=−= (3.75)
В
интегральной
форме
( ) ( )
1122122
тех
1
1
1
vpvp
n
n
TTR
n
n
l −
−
−=−
−
−=
−
. (3.76)
Сравнивая
(3.74)
и
(3.76),
получаем
212
тех
1 −−
= nll .
(3.77)
Связь
между
параметрами
в
политропическом
процессе
определяется
выражениями
n
n
nn
p
p
v
v
T
T
1
2
1
1
2
1
1
1
2
2
1
−
−−
=
=
=
ρ
ρ
.
Связь
теплоемкости
политропического
процесса
с
показателем
политропы
Используя
выражение
для
теплоемкости
политропического
процесса
1
−
−
=
n
kn
cc
vn
и
задаваясь
различными
значениями
п
,
найдем
вид
функции
(
)
nfc
n
= .
При
п
=±
∞
vn
cc = ,
при
п
=k 0=
n
c ,
при
п
=1 ±∞=
n
c ,
при
п
=0
pn
cc = .
Определив
характерные
точки
,
можно
построить
график
,
показанный
на
рис
.3
Таким
образом
,
теплоемкость
политропного
процесса
n
c
может
изменяться
от
-
∞
до
+
∞
,
причем
отрицательные
значения
она
принимает
в
интервале
1<n<k..7.
Это
объясняется
тем
,
что
в
процессе
расширения
произведенная
газом
работа
может
превышать
количество
подведенной
теплоты
,
т
.
е
.
в
этом
случае
работа
совершается
не
только
за
счет
подводимой
теплоты
,
но
и
за
счет
убыли
внутренней
энергии
газа
,
что
и
приводит
к
уменьшению
температуры
.
В
таких
процессах
dq>0,
а
dT<0
и
,
следовательно
, 0<=
dT
dq
c
n
n
.
Если
в
процессе
сжатия
количества
отводимой
теплоты
(dq<0)
недостаточно
,
чтобы
процесс
был
изотермическим
,
внутренняя
энергия
газа
будет
расти
(du>0, dT>0),
т
.
е
.
снова
теплоемкость
процесса
отрицательна
.
k
0
1
n
c
n
c
p
c
v
Рис.3.7
26
Три
группы
политропических
процессов
.
Способы
определения
показателя
политропы
Все
политропические
процессы
принято
делить
на
три
группы
.
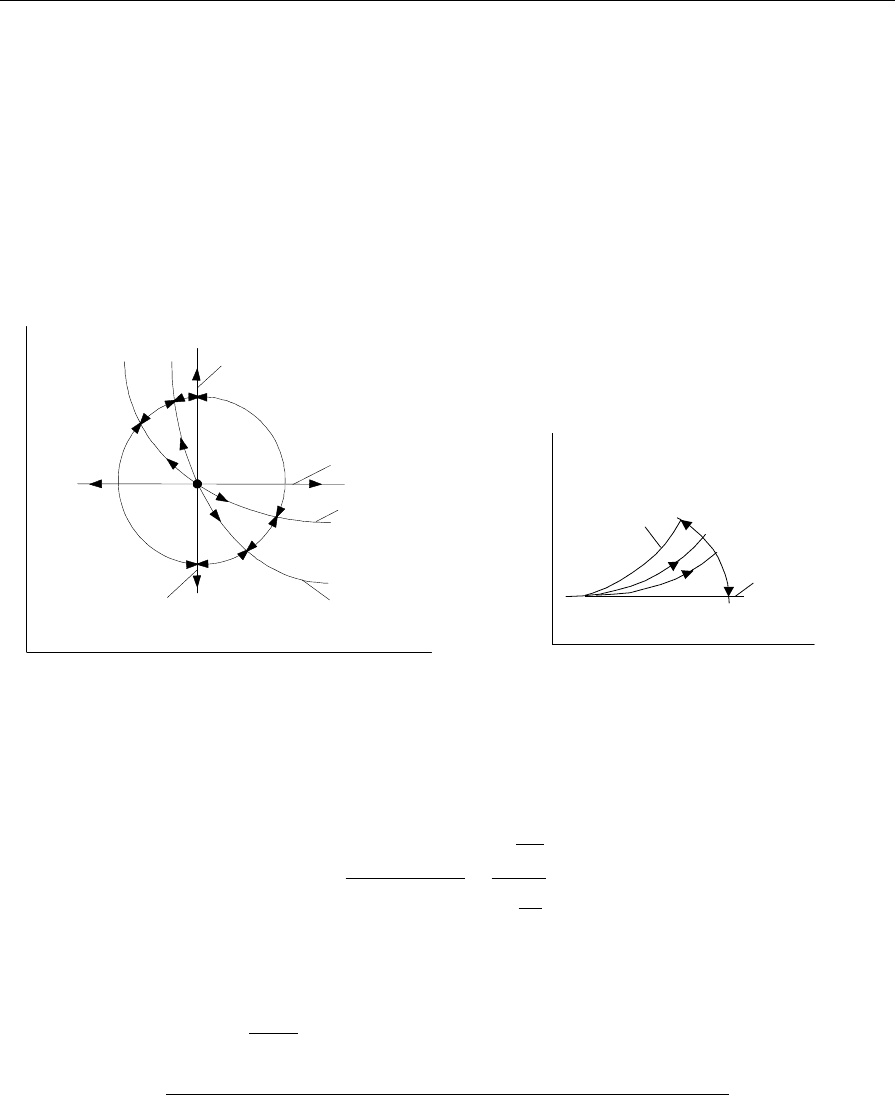
Первая
группа
процессов
(
рис
.3.8)
лежит
между
изохорой
и
изотермой
(±
∞
<
п
<1).
В
этой
группе
в
процессе
расширения
dv>0, dl>0
и
d
Т
>0,
следовательно
,
и
d
и
>0.
Рассматривая
ту
же
группу
в
T-s
диаграмме
,
видим
,
что
ds>0 (
рис
.3.9).
Таким
образом
,
и
dq>0,
т
.
к
.
Tds
dq
=
.
Тогда
c
n
=dq/dT>0 .
При
сжатии
(I
с
) dv<0, dl<0, dT<0, du<0, ds<0, dq<0, c
n
>0.
Для
остальных
групп
процессов
можно
написать
II
p
(1<n<k): dv>0, dl>0, dT<0, du<0, ds>0, dq>0, c
n
<0;
II
c
: dv<0, dl<0, dT>0, du>0, ds<0, dq<0, c
n
<0;
III
p
(k<n<
∞
): dv>0, dl>0, dT<0, du<0, ds<0, dq<0, c
n
>0;
III
c
: dv<0, dl<0, dT>0, du>0, ds>0, dq>0, c
n
>0.
Если
при
проведении
какого
-
либо
политропического
процесса
возможно
определение
начальных
и
конечных
значений
p
и
v,
то
логарифмируя
уравнение
процесса
nn
vpvp
2211
= ,
можно
найти
значение
показателя
политропы
β
tg
ln
ln
lnln
lnln
1
2
2
1
12
21
==
−
−
=
v
v
p
p
vv
pp
n . (3.78)
Кроме
того
,
на
основании
формулы
(3.77),
зная
величины
площадей
между
кривой
процесса
и
осями
координат
в
p-v
диаграмме
,
показатель
политропы
можно
определить
как
отношение
работ
21
l
l
n
−
=
2-
тех
1
.
Процессы
в
одноступенчатом
поршневом
компрессоре
Компрессоры
-
это
машины
,
предназначенные
для
сжатия
газа
и
подачи
его
потребителю
.
По
своему
конструктивному
исполнению
они
делятся
на
объемные
-
статического
сжатия
(
поршневые
и
ротационные
)
и
лопаточные
-
динамического
сжатия
(
осевые
и
центробежные
).
III
c
II
c
I
p
II
p
III
p
I
c
dv=0,n=-
∞
dp=0, n=0
dT=
0,
n=
1
pv
k
=const, n=k
n=
+
∞
p
v
Рис.3.8
dT=
0
T
s
Рис
.3.9
dv=
0
I
p
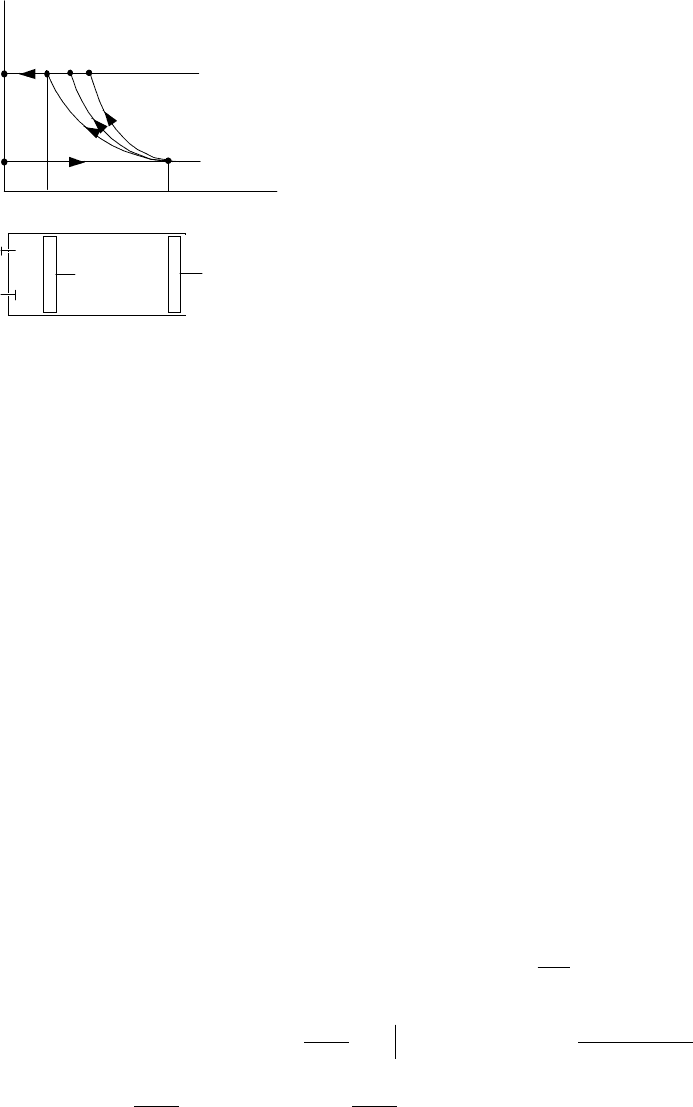
27
Несмотря
на
это
,
термодинамические
процессы
в
них
описываются
одинаковыми
уравнениями
,
если
при
анализе
лопаточных
машин
пренебрегать
кинетической
энергией
газа
(
см
.
ф
-
лу
2.19).
Рассмотрим
одноступенчатый
компрессор
,
основными
элементами
которого
являются
цилиндр
,
поршень
,
впускной
и
выпускной
клапаны
(
рис
.3.10).
Будем
считать
компрессор
идеальным
,
т
.
е
.
процессы
в
нем
протекают
обратимо
,
вредное
пространство
отсутствует
(
объем
,
заключенный
между
днищем
цилиндра
и
поршнем
,
когда
последний
находится
в
верхней
мертвой
точке
),
р
1
=
р
ос
.
Если
бы
удалось
в
процессе
сжатия
отвести
от
газа
количество
теплоты
,
равное
затраченной
работе
,
то
мы
получили
бы
изотермический
процесс
1-2
с
минимально
возможной
работой
сжатия
(
площадь
а
-1-2-b-a).
При
отсутствии
теплообмена
с
ОС
имели
бы
идеальный
адиабатический
процесс
1-2
”
(
площадь
а
-1-2
”
-b-a).
Если
же
в
процессе
сжатия
отводить
теплоту
,
но
в
меньшем
количестве
,
чем
при
изотермическом
процессе
,
то
получим
политропический
процесс
1-2
’
,
у
которого
техническая
работа
сжатия
(
площадь
а
-1-2
’
-b-a)
больше
чем
в
изотермическом
,
но
меньше
чем
в
идеальном
адиабатическом
процессе
.
Поэтому
реальные
поршневые
компрессоры
,
как
правило
,
охлаждаются
водой
,
омывающей
цилиндры
.
В
процессе
а
-1 (
поршень
движется
слева
направо
)
через
впускной
клапан
газ
поступает
в
цилиндр
при
давлении
р
1
=
р
ос
(
в
действительности
р
1
<
р
ос
).
В
положении
1
оба
клапана
закрыты
,
а
поршень
находится
в
нижней
мертвой
точке
.
При
движении
поршня
справа
налево
газ
сжимается
.
Пружина
выпускного
клапана
отрегулирована
так
,
чтобы
на
выходе
из
компрессора
получить
требуемое
давление
р
2
.
В
процессе
2-b
газ
выталкивается
из
цилиндра
и
подается
потребителю
.
Получим
выражение
для
идеальной
работы
компрессора
,
полагая
процесс
сжатия
политропическим
:
( )
.
2
1
2
1
112222112211
к
∫∫
′′
+−−=−+=++=
′′
−
′′
−−
V
V
V
V
ba
pdVVpVpVppdVVpLLLL (3.79)
В
дифференциальной
форме
будем
иметь
VdppdVpVddL −=+−=
)(
к
, (3.80)
или
для
удельной
работы
vdpdl −=
к
.
(3.81)
Преобразуем
(3.79)
используя
уравнение
политропического
процесса
const=
n
pv :
( ) ( )
)82.3(.
1
1
11
1
121122
1122
2211
1
112211
1122112211к
2
1
2
1
TTG
n
nR
VpVp
n
n
n
VpVp
VpVpV
n
VpVpVp
V
dV
VpVpVpLLLL
V
V
nn
V
V
n
n
ba
−
−
−=−
−
−=
=
−
−
+−=
−
+−=
=+−=++=
′′
′
′
−
′
′
−
′′
−−
′
′
∫
Аналогичное
выражение
было
получено
нами
при
рассмотрении
технической
работы
политропического
процесса
(
ф
-
ла
3.76).
Формуле
(3.82),
используя
связь
между
параметрами
,
можно
придать
более
удобный
для
расчетов
вид
введя
степень
повышения
давления
в
компрессоре
π
=
р
2
/
р
1
:
1
2
2
′
2
′
′
a
b
p
1
p
2
p
V
2
V
1
V
Рис.3.10
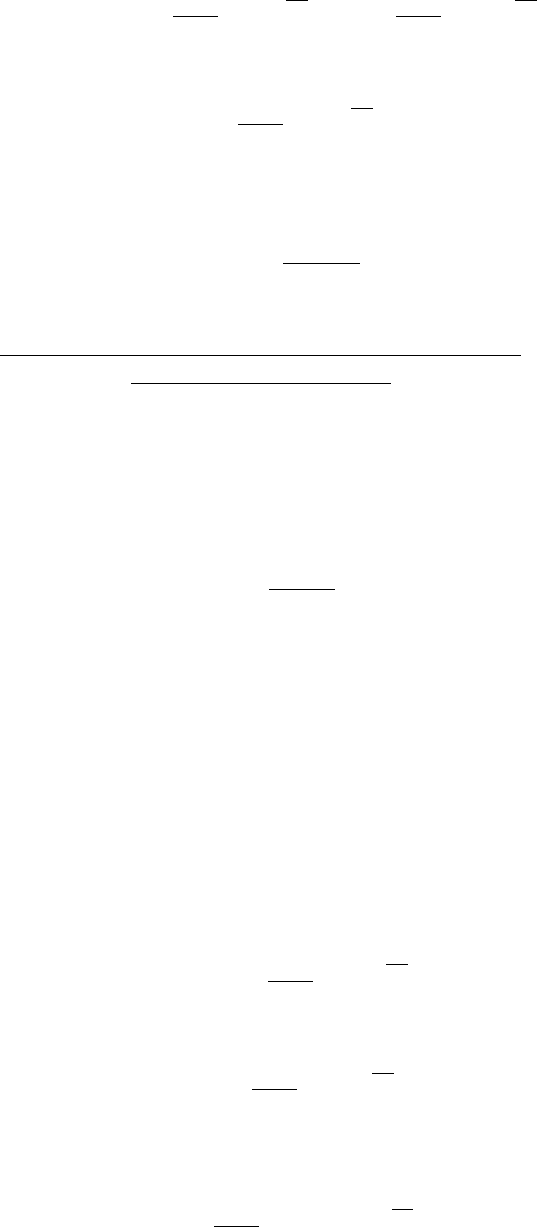
28
−
−
−=
−
−
−=
−−
1
1
1
1
1
11
1
1к
n
n
n
n
Vp
n
n
RT
n
nG
L
ππ
. (3.83)
Мощность идеального компрессора найдем по формуле
−
−
−=
−
1
1
1
1к
n
n
RT
n
Gn
N
π
&
, Вт, (3.84)
где
G
&
, кг/с - производительность компрессора. Потребляемую реальным компрессором
мощность определим с учетом его внутреннего относительного и механического КПД
мехк,
к
кд
ηη
oi
N
N =
. (3.85)
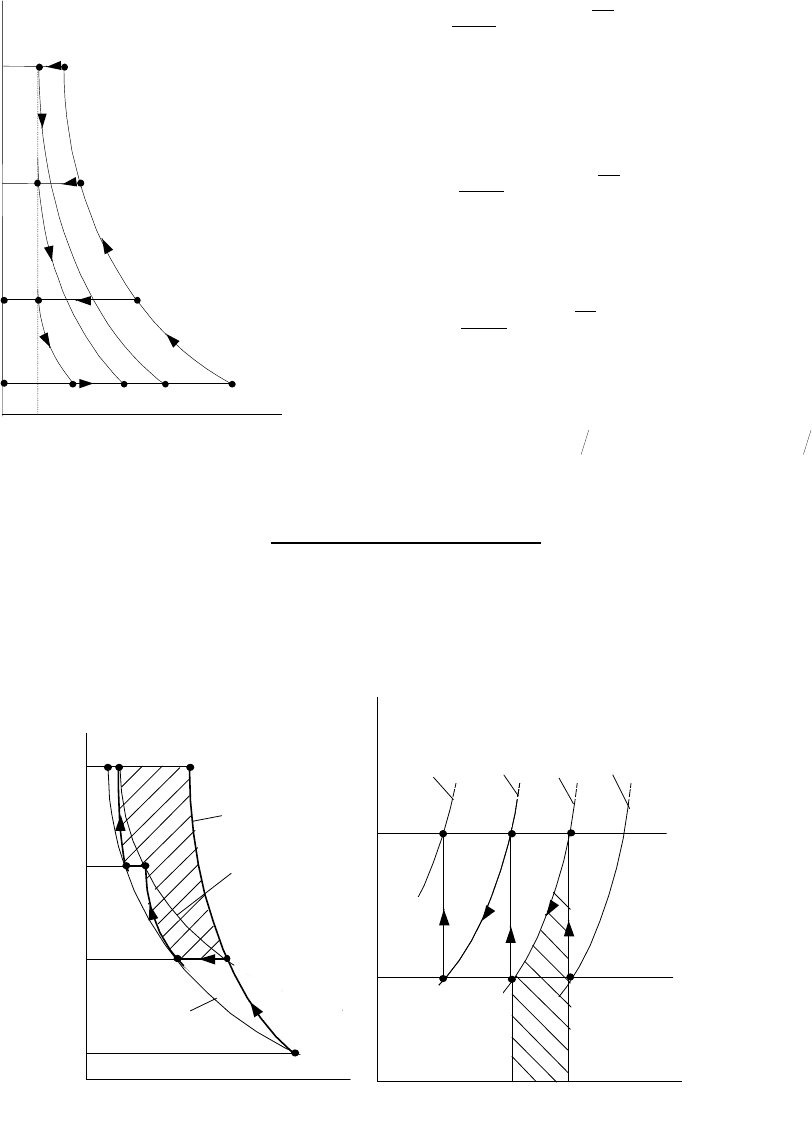
Влияние вредного пространства на эффективность
поршневого компрессора
Наличие клапанного механизма в поршневом компрессоре не позволяет поршню
вплотную подойти к днищу цилиндра. Объем в зазоре между днищем цилиндра и рабочей
поверхностью поршня называется “вредным пространством”. Вредное пространство
снижает производительность компрессора тем сильнее, чем выше степень повышения
давления
π
. Существует такое значение
π
, при котором производительность компрессора
становится равной нулю. Эффективность компрессора оценивается объемным КПД
31
41
VV
VV
v
−
−
=
η
. (3.86)
Рассмотрим процессы в компрессоре при наличии вредного пространства. Сжатие газа
происходит в процессе 1-2. Когда поршень доходит до положения, соответствующего
объему V
2
и давлению
р
2
, открывается выпускной клапан В процессе 2-3 происходит
удаление газа из полости цилиндра в резервуар высокого давления (совершается работа
проталкивания).. В процессе 3-4 расширяется газ, оставшийся во вредном пространстве с
падением давления от
р
2
до
р
4
=
р
1
=
р
ос
, после чего открывается впускной клапан и
начинается процесс 4-1 всасывания новой порции газа. Из рис.3.11 видно, что чем выше
конечное давление за компрессором, тем меньше объем газа, поступающего в цилиндр
(сравните процессы 14
и
,14,14
−
′
′
−
′
−
).
Определим
работу
и
мощность
компрессора
при
наличии
вредного
пространства
.
Техническая
работа
сжатия
,
изображаемая
площадью
а
-
1-2
-b-a
,
равна
−
−
−=
−
−
1
1
1
11.)21(
n
n
тех
Vp
n
n
L
π
, (
а
)
техническая
работа
расширения
(
пл
. 3-4-
a-b-
3)
−
−
=
−
−
1
1
1
41.)43(
n
n
тех
Vp
n
n
L
π
. (b)
Алгебраически
складывая
(
а
)
и
(b),
получим
работу
идеального
компрессора
при
наличии
вредного
пространства
( )
−−
−
−=
−
1
1
1
411к
n
n
VVp
n
n
L
π
, (3.87)
но
(
)
1д411
RTGVVp =−
,
тогда
вместо
(3.87)
можно
написать
29
−
−
−=
−
1
1
1
1дк
n
n
RTG
n
n
L
π
,
Дж
. (3.88)
Мощность
,
необходимая
для
привода
компрессора
,
определяется
работой
,
затрачиваемой
в
единицу
времени
−
−
−=
−
1
1
1
1дк
n
n
RTG
n
n
N
π
&
,
Вт
. (3.89)
Разделив
(3.88)
на
G
д
,
найдем
удельную
работу
компрессора
−
−
−=
−
1
1
1
1к
n
n
RT
n
n
l
π
,
Дж
/
кг
. (3.90)
Отметим
,
что
формально
запись
формулы
(3.88)
ничем
не
отличается
от
(3.83),
но
в
(3.83)
масса
газа
больше
:
(
)
1411д111
RTVVpGRTVpG −=>=
.
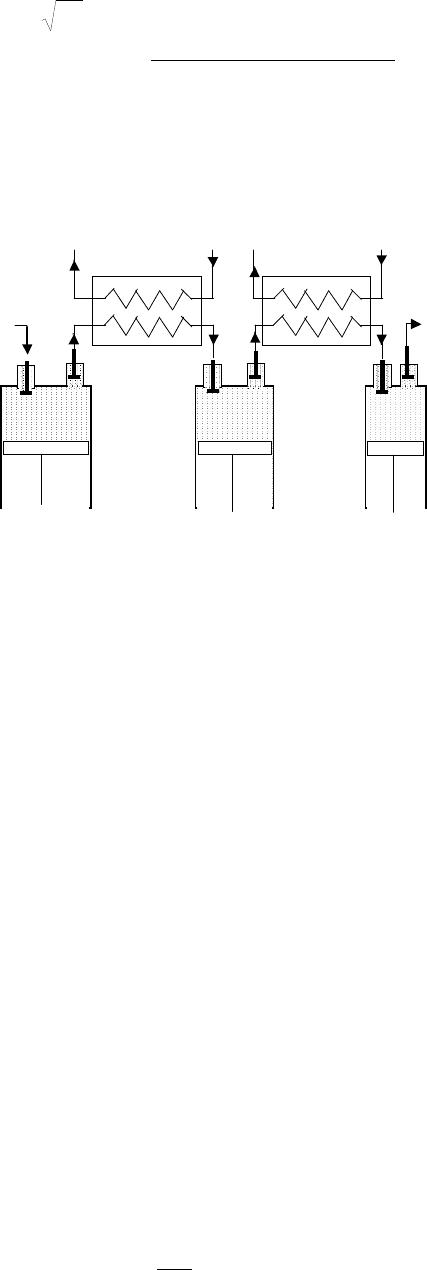
Многоступенчатое
сжатие
Для
получения
давления
газа
р
2
>1
МПа
используют
многоступенчатые
компрессоры
с
промежуточным
охлаждением
газа
в
холодильниках
.
На
рис
.3.12
показаны
процессы
в
трехступенчатом
компрессоре
.
Будем
считать
,
что
процессы
сжатия
протекают
по
изоэнтропам
,
а
процессы
отвода
теплоты
в
холодильниках
I
и
II
происходят
при
dp=
0.
Из
рисунка
видно
,
что
если
бы
сжатие
было
одноступенчатым
(
изоэнтропа
2
1
′
′
′
−
),
то
в
точке
2
′
′
′
температура
была
бы
значительно
выше
,
чем
в
состоянии
2
′
′
,
что
отрицательно
сказалось
бы
на
смазке
трущихся
поверхностей
цилиндра
и
поршня
:
из
-
за
высокой
температуры
снижается
вязкость
масла
,
возможно
возгорание
паров
и
коксование
масла
.
Помимо
снижения
температуры
газа
на
выходе
компрессора
,
применение
многоступенчатого
сжатия
с
промежуточным
отводом
теплоты
в
процессах
2-3
и
32
′
−
′
приводит
к
снижению
технической
работы
на
величину
закрашенной
площади
2223232
−
′
′
′
−
′
′
−
′
−
′
−
−
.
Для
того
чтобы
работа
многоступенчатого
компрессора
была
V
1
4
′′
4
′
4
a
2
b 3
2
′
3
′
2
′
′
3
′
′
p
p
2
′′
p
2
′
p
2
p
1
=
p
oc
Рис.3.11
1
2
3
2
′
3
′
2
′′′
2
′′
3
′
′
ds=
0
dT=
0
dT=
0
p
2
′′
p
2
′
p
2
p
1
=
p
oc
p
v
T
1
T
2
T
a
b
1
2
3
2
′
3
′
2
′
′
s
p
2
p
1
p
2
′
p
2
′′
Рис
. 3.12
а
,
б
30
минимальной
,
необходимо
чтобы
степень
повышения
давления
во
всех
ступенях
была
одна
и
та
же
,
т
.
е
.
n
кст
ππ
=
,
где
п
-
число
ступеней
.
Струйные
компрессоры
Струйные
компрессоры
в
энергетике
выполняют
,
как
правило
,
вспомогательную
роль
.
Например
,
в
паротурбинных
установках
они
используются
для
отсоса
воздуха
из
конденсатора
,
препятствующего
конденсации
пара
на
наружных
поверхностях
трубок
,
внутри
которых
течет
охлаждающая
вода
.
Принцип
работы
струйного
компрессора
(
эжектора
)
основан
на
передаче
кинетической
энергии
от
высокоскоростного
активного
потока
к
пассивному
(
давление
которого
необходимо
повысить
)
в
процессе
их
смешения
.
Эжектор
состоит
четырех
основных
элементов
:
разгонного
сопла
,
пассивного
сопла
,
камеры
смешения
и
диффузора
,
в
котором
кинетическая
энергия
переходит
в
потенциальную
с
ростом
давления
.
Достоинство
эжектора
-
простота
конструкции
,
отсутствие
движущихся
частей
,
недостаток
-
низкая
эффективность
из
-
за
значительной
потери
кинетической
энергии
при
смешении
,
которая
пропорциональна
квадрату
разности
скоростей
смешивающихся
потоков
.
Рассмотрим
процессы
в
эжекторе
,
показанном
на
рис
.3.13.
Полная
энергия
потока
на
входе
в
активное
сопло
характеризуется
энтальпией
торможения
*
1
i
(
если
пренебречь
потенциальной
энергией
положения
)
пассивного
-
*
3
i
.
Точка
2
характеризует
состояние
потока
на
срезе
активного
сопла
при
изоэнтропном
расширении
1-2.
Реальный
процесс
расширения
из
-
за
действия
сил
трения
протекает
по
кривой
1-2
д
.
Аналогично
для
пассивного
сопла
будем
иметь
процесс
3-4
д
.
Если
бы
процесс
смешения
потоков
был
обратимым
,
то
после
изобарного
смешения
в
камере
поток
характеризовался
бы
точкой
5,
при
не
изобарном
смешении
-
точкой
5
′
.
Из
-
за
наличия
ударных
потерь
и
трения
в
камере
смешения
энтальпия
потока
увеличивается
на
труд
iii
∆+∆=∆ .
Точка
5
д
характеризует
состояние
потока
перед
диффузором
.
В
результате
восстановления
давления
в
диффузоре
с
учетом
действия
сил
трения
(
процесс
5
д
-6
д
)
на
срезе
диффузора
статическое
давление
равно
р
6д
.,
а
с
учетом
кинетической
энергии
-
p
*
6д
Следовательно
,
в
эжекторе
статическое
давление
пассивного
агента
увеличилось
от
р
3
до
p
6д
,
т
.
е
.
эжектор
действует
как
компрессор
.
Если
процессы
в
эжекторе
будут
организованы
неудовлетворительно
,
точка
*
д
6
будет
перемещаться
вправо
по
прямой
=
*
см
i
const
и
степень
повышения
давления
по
заторможенным
параметрам
*
3
*
6
д
*
p
p
=
π
будет
уменьшаться
.
1
2
2
′
2
′
′
3
3
′
I
II
Рис
. 3.12
в
