Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.

41
где
q
IIд
-
действительное
количество
теплоты
,
отданное
холодному
источнику
.
Вычитая
(b)
из
(
а
),
определим
потерю
работоспособности
нд цид цпр
sTlll
II
∆=−=
, (4.31)
которая
в
T-s
диаграмме
изображена
заштрихованной
площадью
b-
4-4
д
-
c-b
.
Таким
образом
,
чтобы
определить
действительную
работу
цикла
Карно
,
необходимо
из
идеальной
работы
вычесть
потерю
работоспособности
(
)
нприд цд ц
sTsTTlll
IIIII
∆−∆−=−=
(4.32)
Цикл
Карно
с
внешней
необратимостью
Если
бы
процесс
передачи
теплоты
от
горячего
источника
к
рабочему
телу
цикла
Карно
был
обратимым
,
то
0
=
∆
T
,
а
работа
идеального
цикла
(
)
гихигиид ц
sTTl ∆−=
. (
а
)
При
наличии
температурного
напора
T
∆
(
см
.
рис
.4.13)
действительная
работа
цикла
(
)
ртд ц
sTTl
III
∆−=
. (b)
Вычитая
(b)
из
(
а
),
определим
потерю
работоспособности
,
ртхиртгихигигипр
sTsTsTsTl
I
∆+∆−∆−∆=
но
II
qsTsT =∆=∆
ртгиги
,
тогда
(
)
нхигиртхипр
sTssTl ∆=∆−∆=
(4.33)
(
см
.
заштрихованную
площадь
на
рис
. 4.13).
Как
и
в
предыдущем
примере
,
действительную
работу
цикла
найдем
из
выражения
(
)
нхигихигиприд цд ц
sTsTTlll ∆−∆−=−=
. (4.34)
.
Движение
газа
в
адиабатической
трубе
при
наличии
трения
Мысленно
заключим
некоторый
объем
газа
,
имеющий
среднюю
скорость
с
1
и
массу
G
,
между
двумя
невесомыми
поршнями
,
движение
которых
относительно
центра
тяжести
газового
элемента
сделаем
невозможным
,
наложив
связи
.
Так
как
вся
кинетическая
энергия
после
остановки
газового
элемента
пошла
на
работу
против
сил
трения
,
то
можно
написать
( )
1212тртр
2
1
2
TTcGUUQL
c
G
v
−=−===
,
∆
s
∆
s
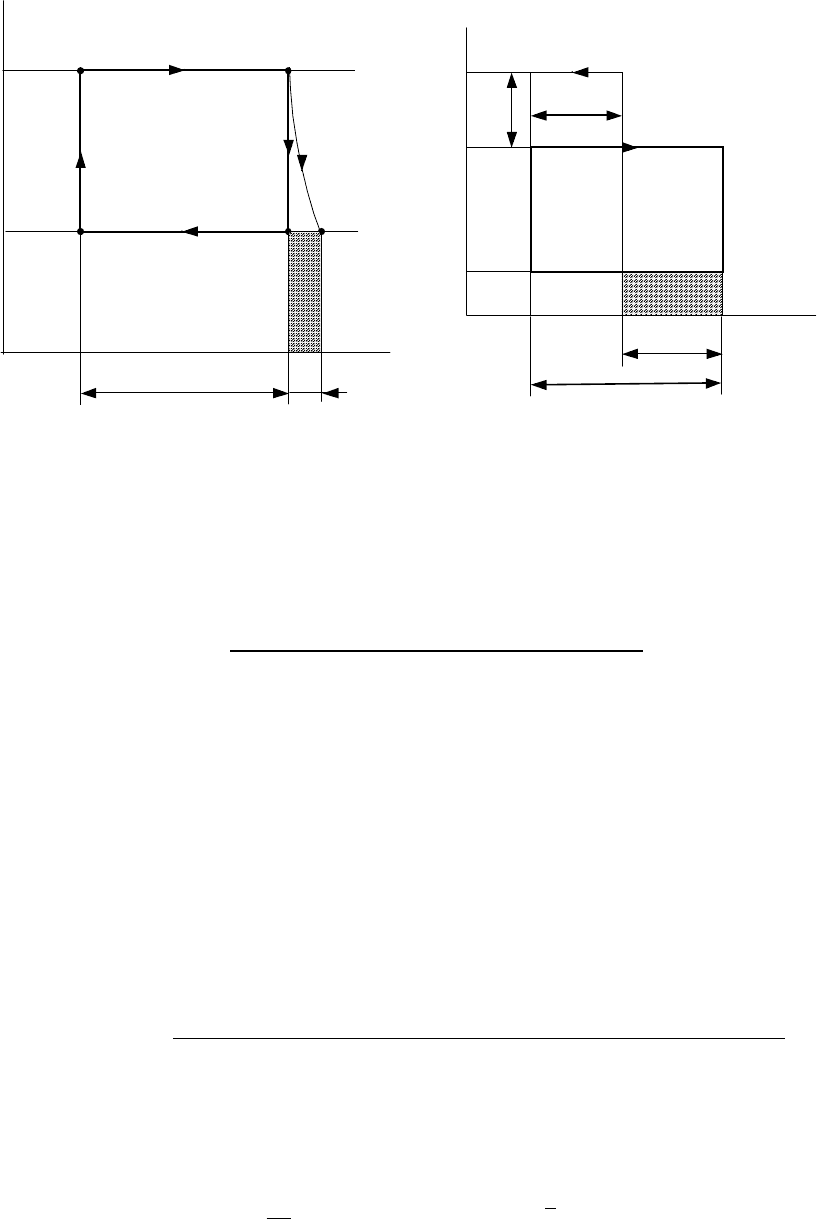
н
1
2
3
a
b
c
4
4
д
Рис
.4.12
T
T
I
T
II
s
∆
s
н
∆
Т
Т
ги
Т
хи
=
Т
II
Т
I
∆
s
ги
∆
s
рт
s
Т
Рис.4.13

42
т
.
е
.
в
изохорном
процессе
к
газовому
элементу
была
подведена
теплота
трения
Q
тр
(
см
.
рис
.4.14,
процесс
1-2).
связь
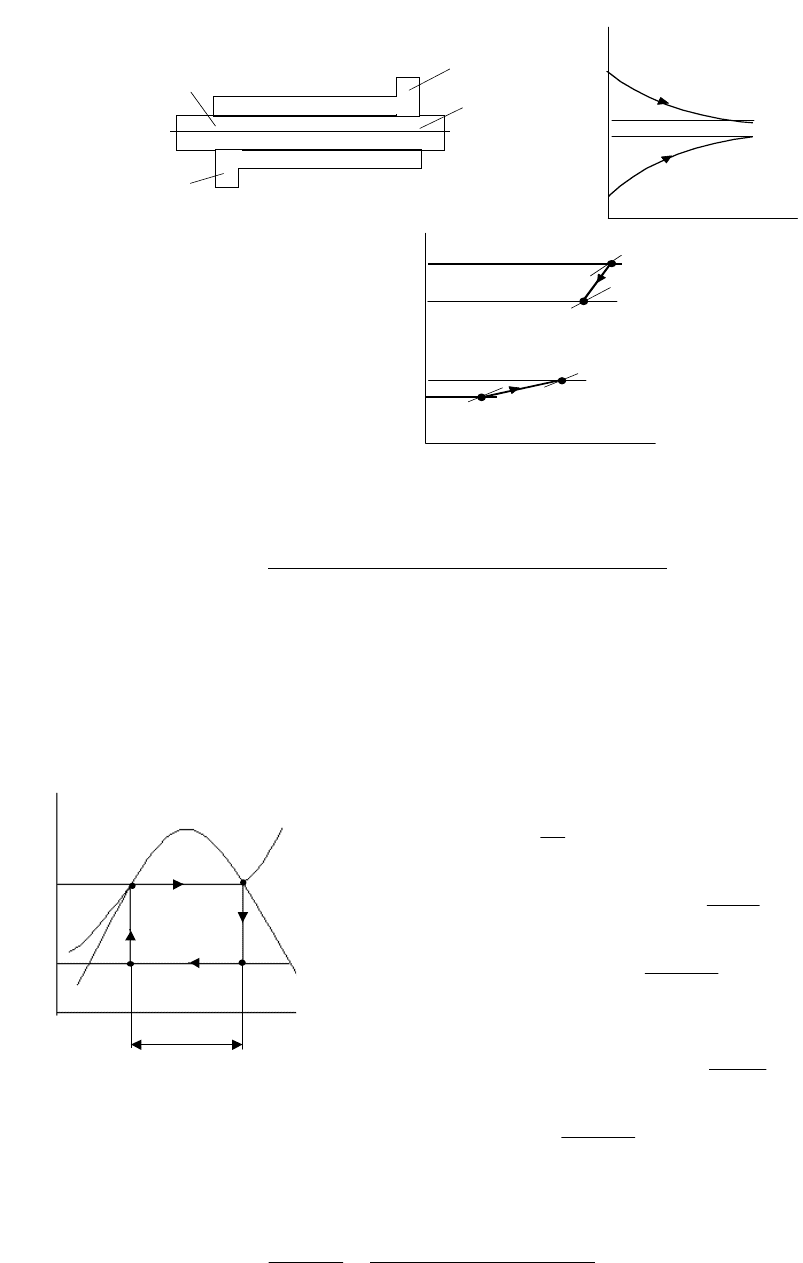
Рис
.4.14
3
2
1
Т
3
Т
2
Т
1
ds=
0
dv=
0
q
тр
р
1
р
2
р
v
Теперь
уберем
наложенные
связи
и
позволим
газу
расширяться
обратимо
по
изоэнтропе
до
давления
р
1
так
,
чтобы
не
произошло
никаких
изменений
как
в
самой
ТС
,
так
и
в
окружающей
среде
(
процесс
2-3).
Так
как
Т
3
>
Т
1
,
то
0ln
1
3
н
>=∆
T
T
cs
p
. (4.35)
Таким
образом
,
течение
газа
с
трением
порождает
внутреннюю
необратимость
,
ведущую
к
росту
энтропии
.
Передача
теплоты
в
теплообменном
аппарате
В
рассматриваемом
примере
имеет
место
как
внешняя
необратимость
,
обусловленная
передачей
теплоты
от
греющего
потока
к
нагреваемому
при
конечной
разности
температур
,
так
и
внутренняя
,
возникающая
из
-
за
наличия
гидравлического
сопротивления
приводящего
к
падению
давления
вдоль
тракта
.
Рассмотрим
процесс
передачи
теплоты
от
одного
потока
к
другому
при
конечной
разности
температур
в
простейшем
теплообменном
аппарате
"
труба
в
трубе
"
и
покажем
,
что
внешняя
и
внутренняя
необратимость
приводят
к
увеличению
энтропии
ТС
“
поток
-
поток
“.
Будем
считать
,
что
греющим
потоком
является
поток
с
расходом
I
G
&
,
а
нагреваемым
-
с
расходом
II
G
&
.
Процессы
,
протекающие
в
теплообменном
аппарате
(
ТА
),
показаны
на
рис
.4.15.
Рисунок
4.15
б
иллюстрирует
изменение
температур
агентов
вдоль
поверхности
теплообмена
F
,
а
4.15
в
-
показывает
процессы
в
T-s
диаграмме
при
наличии
гидравлических
потерь
в
трактах
.
Так
как
в
нашем
случае
,
**
III
IdId
&&
−=
то
пренебрегая
кинетической
энергией
потоков
,
после
интегрирования
получим
)()(
1234
TTcGTTcG
pIIpIIII
−−=−
&&
, (4.36)
откуда
можно
определить
температуру
T
2
или
T
4
.
Приращение
энтропии
потоков
найдем
из
выражений
=
−
=∆
1
2
1
2
lnln
p
p
R
T
T
cGS
IpIII
&&
+
−
2
1
2
1
lnln
p
p
R
T
T
cG
IpII
&
, (4.37)
+
=
−
=∆
4
3
3
4
3
4
3
4
lnlnlnln
p
p
R
T
T
cG
p
p
R
T
T
cGS
IIpIIIIIIpIIIIII
&&&
(4.38)
43
Отметим
,
что
последние
слагаемые
в
формулах
(4.37)
и
(4.38),
которые
отражают
увеличение
энтропии
за
счет
внутренней
необратимости
,
всегда
положительны
.
Для
всей
системы
можно написать
0
>∆+∆=∆
IIIC
SSS
&&&
.
I
G
&
II
G
&
T
2
T
3
T
1
T
4
а
T
1
T
3
T
2
T
4
T
4
T
4
T
F
б
T
1
T
3
T
2
T
4
T
в
p
1
p
2
p
3
p
4
I
II
I
II
S
&
Рис
.4.15
Термодинамическая
шкала
температур
Температура
,
показываемая
жидкостным
термометром
,
отражает
термометрические
свойства
вещества
.
Однако
в
термодинамике
температура
является
термодинамическим
потенциалом
и
,
следовательно
,
не
должна
зависеть
от
физических
свойств
вещества
.
Метод
построения
термодинамической
(
абсолютной
)
шкалы
температур
был
разработан
Томсоном
(
лорд
Кельвин
, 1824-1907).
Идея
метода
-
преобразование
теплоты
в
работу
.
Рассмотрим
идеальный
цикл
Карно
,
осуществляемый
в
двухфазной
области
(
см
.
процессы
в
водяном
паре
)
в
интервале
температур
от
Т
I
до
Т
II
.
(
)
sTTqql
IIIIII
∆−=−=
ц
, (
а
)
но
I
I
T
q
s =∆
,
тогда
(
а
)
можно
переписать
в
виде
I
I
III
T
Tq
qql
∆
=−=
ц
, (b)
откуда
T
qq
q
T
III
I
I
∆
−
=
. (4.39)
Определим
температуру
Т
II
( )
ΙΙ
∆
=∆−=−=
T
Tq
sTTqql
II
IIIIIIц
,
⇒
T
qq
q
T
III
II
II
∆
−
=
. (4.40)
Если
в
качестве
реперных
точек
взять
точку
кипения
воды
и
точку
плавления
льда
при
нормальном
давлении
,
то
точно
поставленный
опыт
дает
:
73,3
9948,16507548,2295
7548,2295
=
−
=
−
III
I
qq
q
,
s
T
T
I
T
II
1
2
3
4
∆
s
Рис.4.16
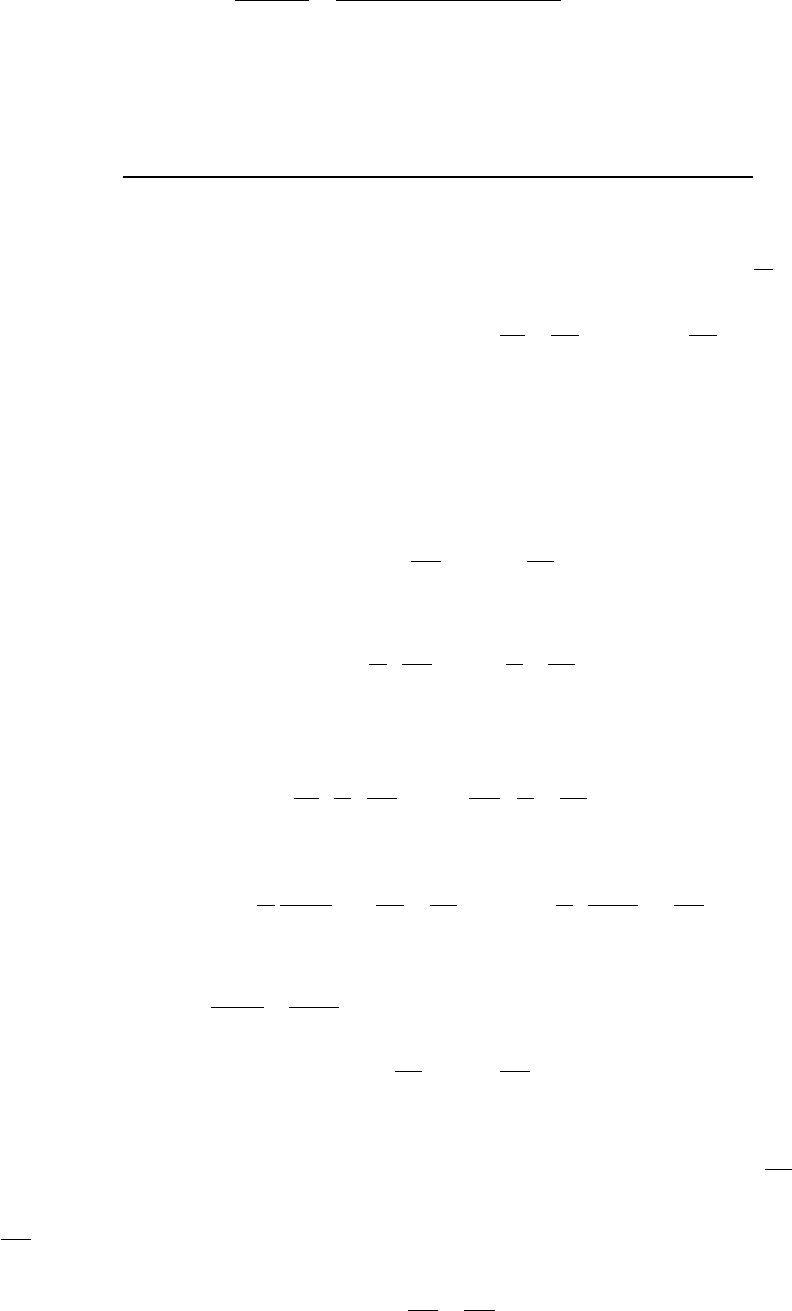
44
73,2
9948,16507548,2295
9948,1650
=
−
=
−
III
II
qq
q
.
Разбивая
шкалу
на
100
делений
,
т
.
е
.
принимая
∆
Т
=100,
получим
Т
I
=373
К
,
Т
II
=273
К
.
Таким
образом
,
полученная
термодинамическая
шкала
не
зависит
от
термометрических
свойств
вещества
.
Тождественность
газовой
и
термодинамической
температур
Покажем
тождественность
термодинамической
и
газовой
температуры
θ
,
измеряемой
газовым
термометром
,
в
котором
используется
идеальный
газ
,
подчиняющийся
уравнению
θ
Rpv
=
.
Так
как
газовый
термометр
работает
при
v=
const,
то
const
=
θ
p
.
Для
двух
точек
на
изохоре
можно
написать
1
12
21
1
22
p
pp
p
θθ
θθ
=⇒=
.
Сделаем
предположение
,
что
между
газовой
и
термодинамической
температурами
существует
связь
(
)
T
ϕθ
= .
Напишем
объединенный
закон
термодинамики
для
обратимого
процесса
pdvduTds
+
=
, (
а
)
но
),(
vTfu
=
,
тогда
pdvdv
v
u
dT
T
u
Tds
Tv
+
∂
∂
+
∂
∂
= . (b)
Разделим
(b)
на
Т
dvp
v
u
T
dT
T
u
T
ds
Tv
+
∂
∂
+
∂
∂
=
11
. (
с
)
Так
как
энтропия
является
функцией
состояния
и
зависит
от
двух
термических
параметров
T
и
v
,
то
накрест
взятые
производные
от
(
с
)
равны
между
собой
,
т
.
е
.
v
T
T
v
p
v
u
TTT
u
Tv
+
∂
∂
∂
∂
=
∂
∂
∂
∂
11
. (d)
Взяв
частные
производные
из
(d),
получим
∂
∂
+
∂∂
∂
+
+
∂
∂
−=
∂∂
∂
vT
T
p
vT
u
T
p
v
u
TTv
u
T
2
2
2
111
. (
е
)
Из
курса
высшей
математики
известно
,
что
смешанные
производные
не
зависят
от
порядка
их
взятия
,
т
.
е
.
v
T
u
T
v
u
∂∂
∂
=
∂∂
∂
22
,
тогда
вместо
(
е
)
можно
написать
p
T
p
T
v
u
vT
−
∂
∂
=
∂
∂
. (4.41)
Выражение
(4.41)
называется
дифференциальным
уравнением
состояния
реального
газа
.
Для
идеального
газа
было
показано
(
см
.
опыт
Гей
-
Люссака
),
что
0
=
∂
∂
T
v
u
,
т
.
е
.
0
=−
∂
∂
p
T
p
T
v
,
но
мы
предположили
,
что
(
)
T
ϕθ
= ,
следовательно
,
0
=−
∂
∂
p
dT
dp
T
v
θ
θ
, (4.42)

45
но
θθ
p
v
Rp
v
==
∂
∂
,
тогда
0
=− p
dT
dp
T
θ
θ
.
Разделив
переменные
,
получим
T
dTd
=
θ
θ
.
Интегрирования
последнего
равенства
дает
C
T
ln
ln
ln
+
=
θ
,
или
kT
=
θ
. (4.43)
Если
выбрать
одинаковую
единицу
измерения
температуры
,
то
k
=1, a
θ
=T
(
см
.
рис
.4.17).
В
дальнейшем
мы
не
будем
делать
различия
между
газовой
и
термодинамической
(
абсолютной
)
температурами
.
Энтропия
и
термодинамическая
вероятность
Великий
Людвиг
Больцман
(1844-1906),
создавший
кинетическую
теорию
газов
,
рассматривая
процессы
в
газах
,
пришел
к
выводу
,
что
система
,
предоставленная
самой
себе
,
переходит
из
менее
вероятного
состояния
в
более
вероятное
,
что
позволило
ему
установить
связь
между
энтропией
S
и
термодинамической
вероятностью
W
.
Под
термодинамической
вероятностью
понимают
число
различных
микросостояний
,
реализующих
данное
макросостояние
системы
(
в
квантовой
механике
W
есть
число
квантовых
состояний
).
По
Планку
,
∏
=
i
i
n
N
W
!
!
,
где
i
i
i
nnN ,
∑
= -
частиц
в
i-
м
состоянии
.
Найдем
связь
между
энтропией
и
термодинамической
вероятностью
.
Для
термодинамической
системы
,
состоящей
из
двух
подсистем
,
можно
написать
:
21
SSS += , (a)
21
WWW ⋅= . (b)
Полагая
,
что
(
)
WS
ϕ
= ,
вместо
(
а
)
будем
иметь
(
)
(
)
(
)
2121
WWWW
ϕϕϕ
+= . (
с
)
Продифференцируем
(
с
)
сначала
по
W
1
:
(
)
(
)
1221
WWWW
ϕϕ
′
=
′
, (d)
а
затем
по
W
2
(
)
(
)
0
212121
=
′
+
′
′
WWWWWW
ϕϕ
,
но
21
WWW = ,
следовательно
,
(
)
(
)
0
=
′
+
′
′
WWW
ϕϕ
. (
е
)
Последнее
выражение
перепишем
в
виде
(
)
( )
0=
′
+
′
WW
dW
Wd
ϕ
ϕ
, (f)
разделим
переменные
(
)
( )
0=+
′
′
W
dW
W
Wd
ϕ
ϕ
(g)
и
проинтегрируем
(
)
kWW
lnlnln
=+
′
ϕ
, (h)
откуда
(
)
kWW =
′
ϕ
. (k)
Решим
уравнение
(k)
относительно
ϕ
(W):
(
)
( )
W
dW
kWdkW
dW
Wd
==
ϕ
ϕ
, ,
(
)
1
ln
kWkW +=
ϕ
,
но
(
)
WS
ϕ
= ,
тогда
окончательно
WkS ln
=
(4.44)
45
0
k
=1
θ
T
Рис.4.17

46
(
можно
показать
,
что
23
0
0
1038,1
−
⋅==
N
R
k
Дж
/K -
постоянная
Больцмана
,
а
k
1
=0).
Диалектическое
толкование
второго
закона
термодинамики
Выше
говорилось
,
что
термодинамический
метод
исследования
применим
лишь
к
конечным
системам
.
Применение
его
к
микромиру
,
где
теряются
понятия
теплоты
и
работы
,
а
также
к
бесконечным
системам
приводит
к
ошибочным
выводам
.
Рудольф
Клаузиус
,
применив
второй
закон
термодинамики
к
бесконечной
системе
,
пришел
к
выводу
,
что
рано
или
поздно
наступит
так
называемая
“
тепловая
смерть
вселенной
”.
Он
писал
: “
Энергия
мира
остается
постоянной
,
энтропия
мира
стремится
к
максимуму
”.
Теория
“
тепловой
смерти
”
приводит
нас
к
существованию
Бога
.
Папа
Пий
XII
на
заседании
папской
академии
наук
в
1952
году
говорил
о
существовании
“
Необходимого
Существа
”.
Фридрих
Энгельс
(
см
.
Ф
.
Энгельс
,
Диалектика
природы
,
Госполитиздат
, 1952,
с
.19)
писал
: ”...
материя
во
всех
своих
превращениях
остается
вечно
одной
и
той
же
,
ни
один
из
ее
атрибутов
никогда
не
может
быть
утрачен
и
что
поэтому
с
той
же
самой
признанной
необходимостью
,
с
какой
она
когда
-
нибудь
истребит
на
Земле
свой
высший
цвет
-
мыслящий
дух
,
она
должна
будет
снова
породить
что
-
нибудь
в
другом
месте
и
в
другое
время
”.
В
противовес
Клаузиусу
Больцман
считал
,
что
вселенная
находится
,
вообще
говоря
,
в
состоянии
термодинамического
равновесия
,
однако
в
ней
неизбежно
возникают
сколь
угодно
большие
флуктуации
.
Наблюдения
и
открытия
астрофизиков
показывают
,
что
материя
обладает
никогда
не
утрачиваемой
способностью
к
концентрации
энергии
и
превращению
одних
форм
движения
в
другие
.
5. Приложение второго закона термодинамики к анализу термодинамических
процессов
Средняя
термодинамическая
температура
процесса
При
термодинамическом
анализе
циклов
в
ряде
случаев
удобно
ввести
понятие
средней
термодинамической
температуры
процесса
(
средней
температуры
подвода
или
отвода
теплоты
).
В
этом
случае
работа
цикла
в
T-s
диаграмме
изобразится
в
виде
прямоугольника
.
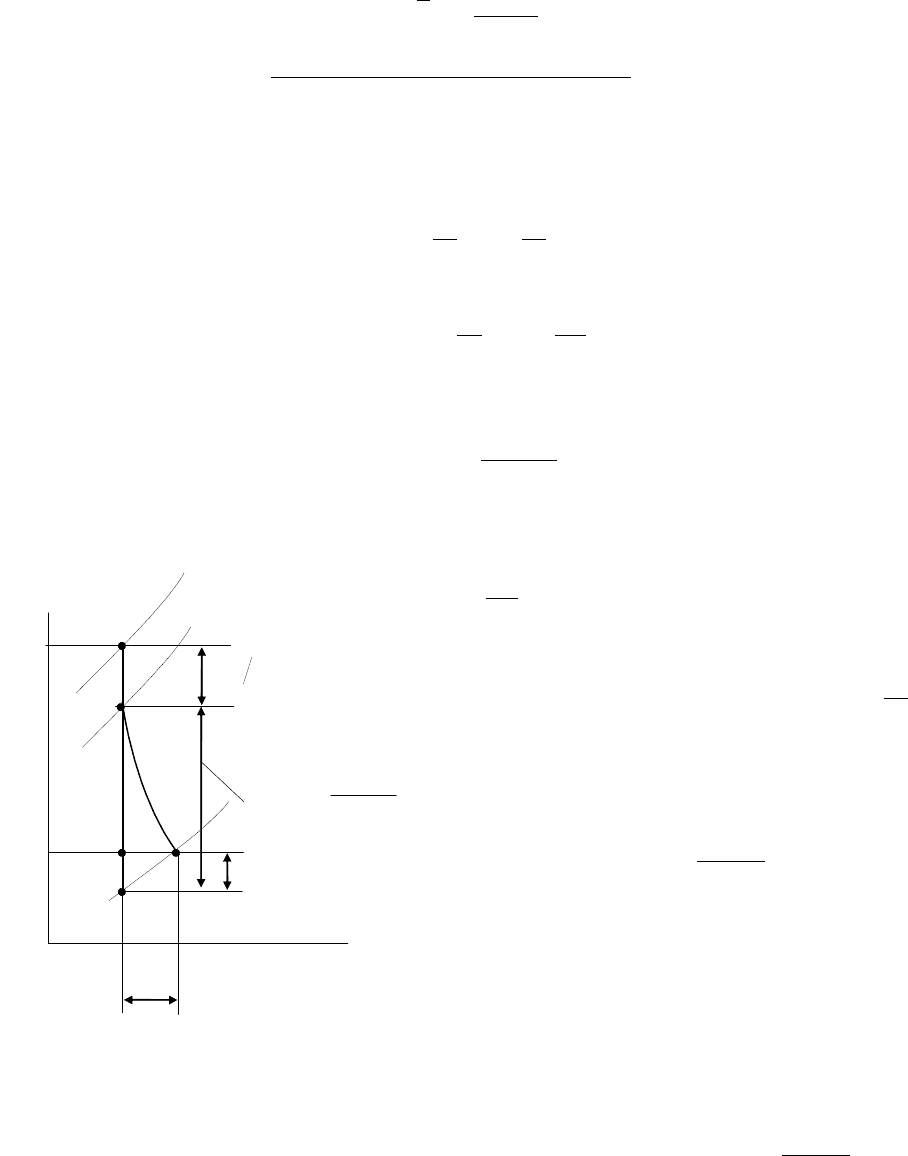
Рассмотрим
политропический
процесс
в
T-s
диаграмме
(
см
.
рис
.5.1).
Для
политропического
процесса
dTcdq
nn
=
или
в
интегральной
форме
(
)
122-1
TTcq
nn
−= . (
а
)
По
определению
T
dq
ds
n
= ,
так
что
после
интегрирования
получаем
1
2
21
ln
T
T
cs
n
=∆
−
. (b)
Умножение
(b)
на
среднюю
температуру
подвода
теплоты
21
−
T
дает
1
2
21
ln
T
T
cTq
ncb
−−
= . (
с
)
Приравнивая
q
b-c
и
q
n1-2
,
найдем
выражение
для
средней
температуры
подвода
теплоты
1
2
12
21
ln
T
T
TT
T
−
=
−
. (5.1)
Т
s
a
d
c
b
∆
s
1-2
1
2
2
1
−
T
Рис
. 5.1
47
Аналогичные
рассуждения
проводятся
и
в
случае
отвода
теплоты
от
термодинамической
системы
.
Так
как
в
T-s
диаграмме
изобары
реальных
веществ
на
пограничных
кривых
имеют
излом
,
то
средняя
температура
процесса
должна
определяться
более
общим
выражением
12
12
21
ss
ii
T
−
−
=
−
. (5.2)
Адиабатическое
течение
с
трением
При
течении
вязкого
газа
в
каналах
часть
кинетической
энергии
газа
расходуется
на
работу
против
сил
трения
,
которая
равна
теплоте
трения
.
Рассмотрим
течение
вязкого
газа
в
сопле
Лаваля
в
i-s
диаграмме
.
Так
как
в
адиабатическом
канале
0
*
=
di
,
то
при
отсутствии
сил
трения
справедливо
равенство
2
2
2
2
2
2
1
1
*
1
c
i
c
ii +=+= .
(
а
)
При
наличии
сил
трения
будем
иметь
2
2
2
д2
д2
2
1
1
*
1
c
i
c
ii +=+= , (b)
где
индекс
“
д
”
характеризует
действительные
значения
величин
.
Приравнивая
(
а
)
и
(b),
получим
2
2
д2
2
2
2д2тр
cc
iii
−
=−=∆ , (
с
)
где
тр
i
∆
-
потеря
кинетической
энергии
,
обусловленная
трением
.
Введем
понятие
коэффициента
скорости
2
д2
с
с
с
=
ϕ
,
с
учетом
которого
перепишем
(
с
)
в
виде
( )
2
1
2
2
2
тр
с
i
c
ϕ
−=∆ .
(5.3)
Для
идеального
сопла
с
ϕ
=1,
а
тр
i∆ =0.
При
этом
имеет
место
максимальное
приращение
кинетической
энергии
21
2
1
2
2
2
ii
cc
−=
−
.
В
T-s
диаграмме
на
рис
.5.3
площадь
под
кривой
процесса
a-1-2
д
-b-a
изображает
теплоту
трения
,
а
∆i
тр
=i
2д
-i
2
отображается
площадью
2-
2
д
-b-a-2
и
часто
называется
термодинамической
потерей
.
Часть
же
теплоты
трения
,
соответствующая
площади
1-
2
д
-2-1,
идет
на
увеличение
энтальпии
потока
и
может
быть
использована
в
процессе
последующего
расширения
.
Покажем
процессы
расширения
в
p-v
диаграмме
(
рис
.5.4).
Здесь
разность
энергий
2
2
1
2
2
cc −
при
изоэнтропийном
расширении
в
процессе
1-2
изобразится
площадью
1-2-m-d-1.
Реальный
процесс
расширения
с
трением
будет
протекать
по
кривой
1-2
д
.
Чтобы
найти
действительное
приращение
кинетической
энергии
,
необходимо
из
точки
2
д
провести
изоэнтальпу
di=0 (
линия
2
д
-
с
)
до
пересечения
с
изоэнтропой
1-2.
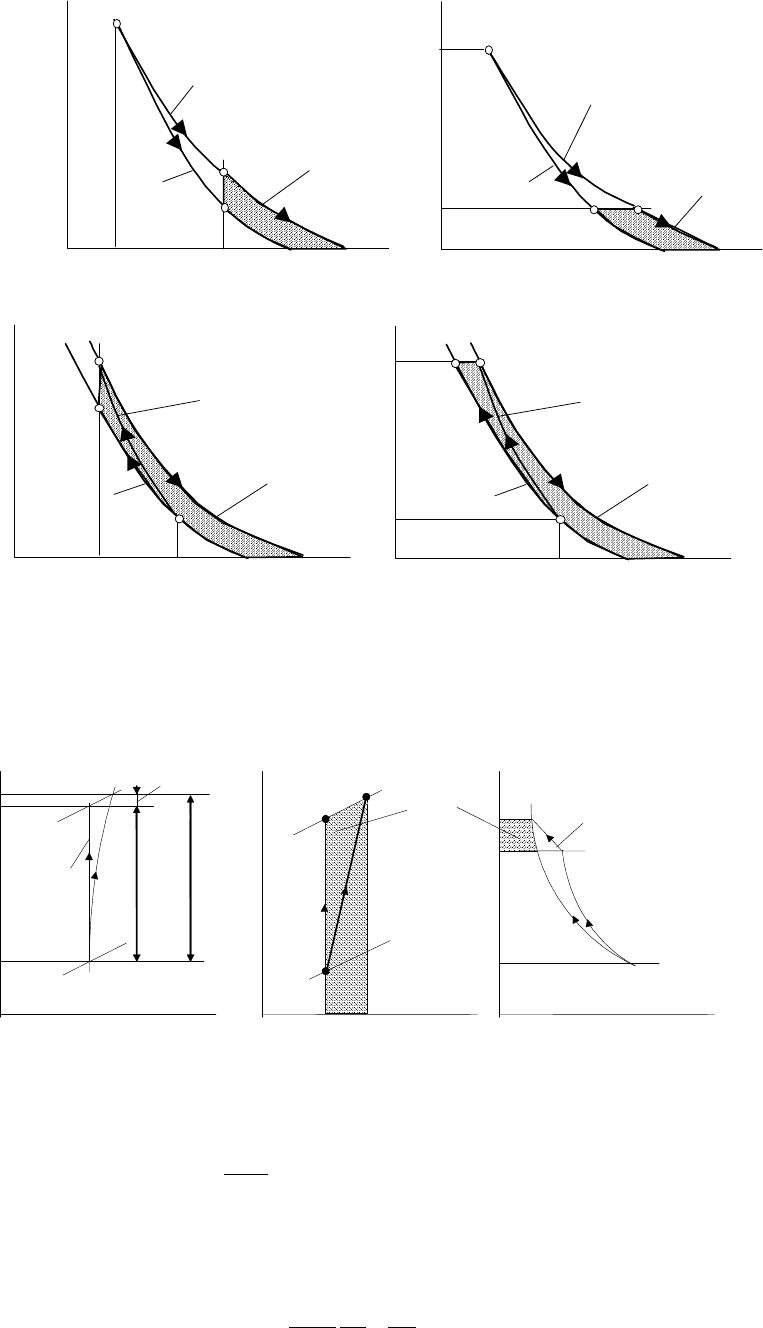
i
1
2
2д
1
*
i
*
p
1
*
p
1
p
2
∆i
тр
i
2
д
s
c
∆s
тр
2
2
1
с
2
2
1
2
2
21
cc
ii
−
=−
Рис
. 5.2

48
Тогда
2
2
1
2
д2
cc −
изобразится
площадью
1-
с
-
е
-d-1,
а
∆i
тр
-
площадью
с
-2-m-e-c.
Вся
теплота
трения
в
p-v
диаграмме
соответствует
площади
1-2
д
-m-e-c-1.
Проведенные
для
сопла
рассуждения
справедливы
и
при
рассмотрении
процессов
в
турбине
.
При
рассмотрении
внутренней
энергии
и
энтальпии
было
показано
,
что
значения
этих
функций
состояния
могут
быть
изображены
в
p-v
диаграмме
в
виде
площадей
(
см
.
рис
.2.5).
Применим
это
положение
при
изучении
процессов
с
трением
.
На
рис
.5.5
а
показан
идеальный
1-2
и
реальный
1-2
д
процессы
расширения
.
При
изоэнтропийном
процессе
работа
изменения
объема
21ид21
uul
−
=
−
изображается
разностью
площадей
1-
с
-
а
-1
и
2-c-b-2.
В
реальном
процессе
1-2
д
из
-
за
действия
сил
трения
внутренняя
энергия
и
2д
в
точке
2
д
будет
больше
и
2
и
изобразится
площадью
2
д
-d-b-
2
д
.
Так
как
д21д21
uul −=
−
,
то
работа
изоэнтропийного
расширения
(
пл
. 1-2-b-a-1)
уменьшится
на
величину
площади
2
д
-d-
с
-2-2
д
,
т
.
е
.
(
)
2д2ид21д21
uull −−=
−−
.
В
процессе
сжатия
с
трением
(
рис
.5.5
б
)
внутрен
няя
энергия
газа
в
точке
2
д
изображается
площадью
2
д
-d-a-2
д
,
а
в
точке
1-
площадью
1-c-b-1,
тогда
действительная
работа
сжатия
l
сж д
изобразится
площадью
2
д
-d-c-1-b-a-2
д
.
Рассматривая
действительную
техническую
работу
расширения
(
рис
.5.5
в
),
видим
,
что
идеальная
работа
(
пл
. 1-2-a-b-1)
уменьшается
на
величину
,
эквивалентную
площади
2
д
-d-c-2-2
д
,
которая
равна
∆i
тр
.
Для
того
чтобы
найти
реальную
техническую
работу
сжатия
(
рис
.5.5
г
)
необходимо
из
площади
2
д
-d-0-
а
-2
д
(
эта
площадь
изображает
энтальпию
i
2д
)
вычесть
площадь
1-
с
-0-b-1,
изображающую
i
1
.
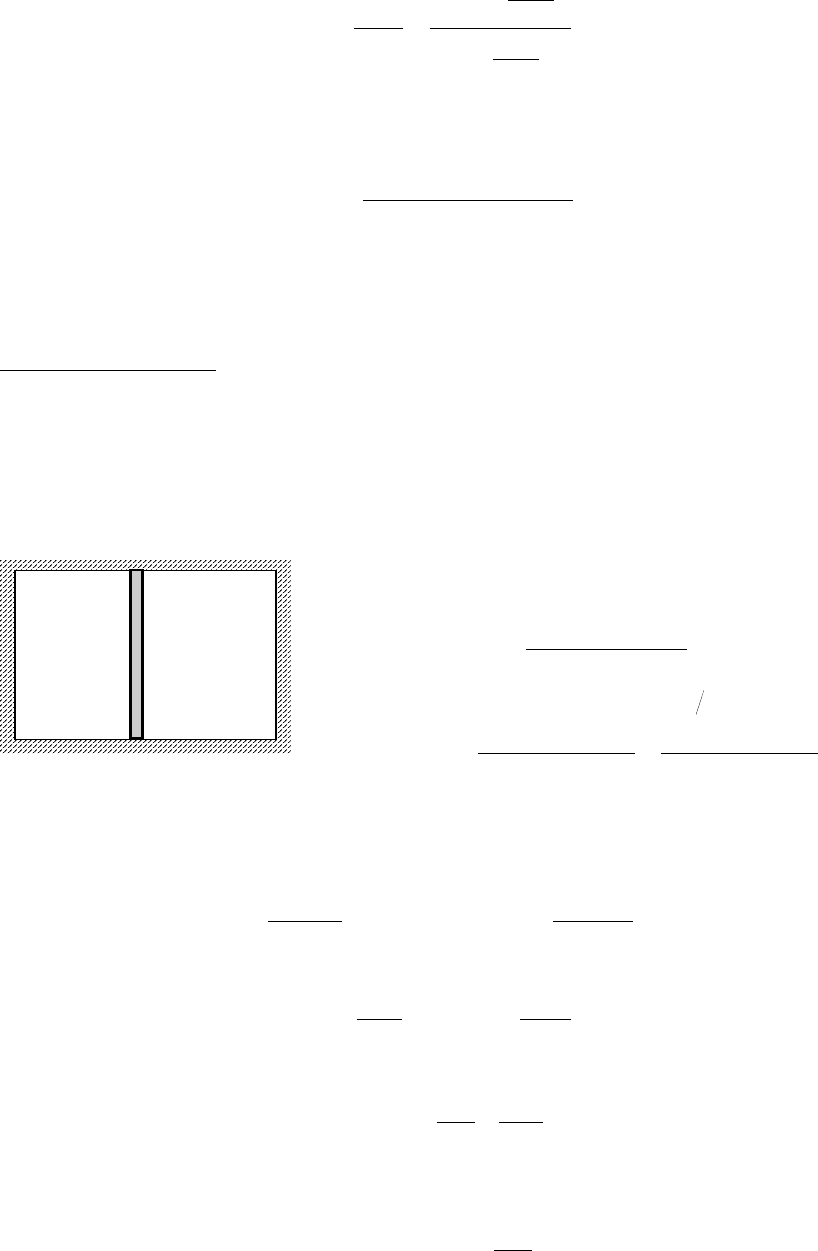
Ниже
приводятся
рисунки
процессов
сжатия
в
компрессоре
в
i-s, T-s
и
p-v
диаграммах
.
Отметим
,
что
в
процессах
сжатия
∆i
тр
=i
2д
-i
2
(
рис
.5.6b,
пл
.
а
-2-2
д
-b-a)
больше
теплоты
трения
(
пл
.a-1-2
д
-b-a),
а
в
процессах
расширения
-
наоборот
(
см
.
рис
.5.4).
Определим
значение
показателя
политропы
при
расширении
идеального
газа
в
адиабатическом
канале
,
если
известен
коэффициент
трения
ξ
.
Так
как
dq
внеш
=0,
то
уравнение
первого
закона
термодинамики
примет
вид
vdpdidq −=
тр
,
но
didq
ξ
=
тр
,
тогда
(
)
01
=−− vdpdi
ξ
или
(
)
01 =−− vdpdTc
p
ξ
. (
а
)
Так
как
R
k
k
c
p
1
−
= ,
то
(
а
)
представим
в
виде
( ) ( ) ( )
0
1
1
1
1 =−
−
−=−
−
− vdppvd
k
k
vdpRdT
k
k
ξξ
. (b)
1
2
2д
T
s
a
b
p
1
p
2
Рис
. 5.3
ds=
0
di=
0
p
1
p
2
p
v
m
e
c
1
2 2д
∆
i
тр
2
2
1
2
д2
сс −
d
Рис
. 5.4
49
Введем
обозначение
( )
1
1
−
−=
k
k
B
ξ
и
преобразуем
(b):
(
)
01
=−+ vdpBBpdv .
Разделив
переменные
,
получим
уравнение
политропического
процесса
с
трением
в
дифференциальной
форме
0
1
=+
− p
dp
v
dv
B
B
,
v
a
b
c
d
0
pv
n
=const
ds=
0
p
2
2
д
1
ds=
0
v
a
b
c
d
0
pv
n
=const
ds=
0
p
2
2
д
1
p
2
p
1
ds=
0
а
в
v
a
b
c
d
0
pv
n
=const
ds=
0
p
2
2д
1
ds=
0
v
a
b
c
d
0
pv
n
=const
ds=
0
p
2
2д
1
ds=
0
p
2
p
1
б
г
Рис
.5.5
∆i
тр
l
к ид
l
к д
ds=
0
i
2
д
i
2
i
2д
2
1
s
p
2
p
1
a
s
2д
2
1
a
b
b
T
p
2
p
1
p
1
2
2д
c
d
e
m
p
1
p
2
∆i
тр
c
v
di=
0
Рис
. 5.6
50
где
( )
( )
1
1
1
1
1
1
−
−
−
−
−
=
−
=
k
k
k
k
B
B
n
ξ
ξ
- (5.4)
показатель
политропы
.
Выражение
(5.4)
имеет
предельный
переход
,
т
.
е
.
при
ξ
=0
получаем
n=k.
Процессы
смешения
Во
многих
энергетических
системах
и
устройствах
имеют
место
процессы
смешения
газов
с
различными
физическими
свойствами
и
параметрами
.
При
этом
возникает
вопрос
о
состоянии
смеси
:
какими
будут
температура
и
давление
смеси
,
насколько
увеличится
энтропия
и
т
.
п
.
Рассмотрим
процессы
смешения
газов
в
объеме
,
в
потоке
и
при
заполнении
сосудов
.
Смешение
в
объеме
.
Для
жесткой
адиабатической
системы
,
состоящей
из
двух
газов
,
разделенных
перегородкой
,
можно
написать
21
UUU
c
+= . (
а
)
Если
убрать
перегородку
между
газами
,
то
внутренняя
энергия
системы
U
c
не
изменится
(
нет
причин
для
ее
изменения
).
Раскрывая
выражение
для
внутренней
энергии
,
перепишем
(
а
)
в
виде
(
)
222111
смсм
21
TcGTcGTcGG
vvv
+
=
+
, (b)
откуда
найдем
температуру
смеси
( )
см21
222111
см
v
vv
cGG
TcGTcG
T
+
+
= . (5.5)
Вводя
понятие
массовой
доли
см
GGg
ii
= ,
перепишем
(5.5)
2211
222111
см
222111
см
vv
vv
v
vv
cgcg
TcgTcg
c
TcgTcg
T
+
+
=
+
= . (5.6)
Для
идеального
газа
21см
ppp
′
+
′
= ,
где
р
′
-
парциальное
давление
газа
.
Из
уравнений
состояния
см11см1
TRGVp =
′
и
см22см2
TRGVp =
′
найдем
парциальные
давления
газов
см
см11
1
V
TRG
p =
′
(
с
),
см
см22
2
V
TRG
p =
′
. (d)
Из
уравнений
состояния
,
записанных
для
газов
до
смешения
,
определим
массу
газов
11
11
1
TR
Vp
G = (
е
) ,
22
22
2
TR
Vp
G = . (g)
Подставляя
(
е
)
и
(g)
соответственно
в
(
с
)
и
(d),
получим
выражение
для
давления
смеси
см
2
22
1
11
см
T
T
rp
T
rp
p
+= , (5.7)
где
r
i
=V
i
/V
см
-
объемная
доля
газов
;
р
1
и
р
2
-
давления
газов
до
смешения
.
В
самом
общем
случае
смешения
п
газов
можно
написать
∑
=
=
n
i
i
ii
T
rp
Tp
1
смсм
. (5.8)
Зная
параметры
газов
до
и
после
смешения
,
можно
найти
увеличение
энтропии
системы
,
вызванное
процессом
образования
смеси
.
Изменение
энтропии
системы
есть
сумма
изменений
энтропии
для
каждого
из
компонентов
:
U
1
,
p
1
,
T
1
U
2
,
p
2
,
T
2
1 2
Рис
. 5.7
