Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.


252
Проинтегрируем (а) с учетом С
1
=0:
2
2
0
42
16
1
4
C
R
RR
AT +
−= . (b)
при
0
RR = :
w
TT = , тогда из (b)
2
2
0
2
0
164
C
RR
AT
w
+
−= ,
2
022
2
0
16
3
16
3
ARTCC
R
AT
ww
−=⇒+= .
Подставляя константу С
2
в (b), получим закон распределения температуры по радиусу
трубы
2
0
2
0
42
16
3
16
1
4
ART
R
RR
AT
w
−+
−= или
w
T
R
R
R
R
AR
T +
−
−
=
4
3
4
1
4
4
0
2
0
2
0
. (22.25)
Определим коэффициент теплоотдачи, используя граничные условия III рода
( )
0
RR
о
w
dR
dT
TT
=
−=−
λα
. (с)
Из (22.25) при R=0 следует :
2
0
16
3
ARTT
w
о
−=− , тогда с учетом (*) имеем
0
2
0
4
1
16
3
ARAR
λα
= , (22.26)
откуда
DR
λ
λ
α
3
8
3
4
0
== . Таким образом, на основном (стабилизированном) участке
течения коэффициент теплоотдачи увеличивается с уменьшением диаметра трубы, так как
уменьшается термическое сопротивление пограничного слоя.
Подставляя
α
в выражение для числа Нуссельта, получаем для основного участка
67,2
3
8
Nu ===
λ
α
D
. (22.27)
Если коэффициент теплоотдачи определять по перепаду между температурой
стенки и средней по сечению температурой потока
( )
∫
=
F
wTdF
wF
T
1
, то Nu = 4,36. (22.28)
Подвод теплоты к капельной жидкости или отвод теплоты от газовой среды приводит к
образованию более заполненного профиля скорости по сравнению с изотермическим
течением, и наоборот (см. рис.22.5 для случая капельной жидкости), что сказывается на
теплоотдаче.
В инженерной практике при расчете теплоотдачи используются критериальные
уравнения, полученные разными авторами на основании экспериментальных
исследований. Так, в (22.29) учитывается влияние свободной конвекции (множитель
(
)
1,0
PrGr ) и длина начального участка с помощью коэффициента
=
D
l
f
l
ε
:

253
( )
l
D
ε
λ
α
1,0
33,032,0
__
PrGrPrRe15,0Nu == . (22.29)
Обычно безразмерная длина начального участка при
ламинарном режиме определяется зависимостью
Re03,0
н
=
D
l
. Существуют и другие формулы, например,
l
l
D
ε
33.0
Pe55,1Nu
= . (22.30)
Следует помнить, что критериальные уравнения
можно использовать только в том диапазоне изменения
определяющих критериев, для которого они были получены.
Теплоотдача в трубах с прямолинейной осью при турбулентном движении
Для определения коэффициента теплоотдачи воспользуемся аналогией Рейнольдса.
Так, при Re=10
5
...10
7
коэффициент сопротивления определяется по формуле
2,0
Re184,0
−
=
ξ
. (22.31)
Используя (22.31) и соотношения PrReStNu
⋅
⋅
=
,
3
2
Pr
2
St
−
=
f
с
,
4
ξ
=
f
с
,
можно получить:
33,08,0
PrRe023,0Nu = , (22.32)
где
λ
α
D
=Nu ,
ν
Dw
=Re .
Чтобы учесть изменение теплофизических свойств потока при подводе или отводе
теплоты, формулу (22.32) записывают в виде:
l
w
f
ε
25,0
43,08,0
Pr
Pr
PrRe023,0Nu
= (22.33)
- формула Михеева. Здесь
f
Pr рассчитан по параметрам жидкости при средней
температуре жидкости,
w
Pr - по параметрам жидкости при температуре стенки. Поправку
(
)
DL
l
//21 +=
ε
вводят для коротких труб, когда L/D<50. Формула (22.34) позволяет
более точно учесть изменение коэффициента теплоотдачи при изменении направления
теплового потока. Так, при нагреве капельной жидкости показатель степени
п
=0,11 , при
охлаждении
п
=0,25 :
n
w
f
−+
=
µ
µ
ξ
ξ
1Pr
8
7,1207,1
PrRe
8
Nu
3
2
, (22.34)
где
( )
.
64,1Relg82,1
1
2
−
=
ξ
Приведенные выше формулы позволяют рассчитывать теплоотдачу и в каналах
некруглого сечения путем введения понятия эквивалентного диаметра
Π
=
F
D
4
экв
, где F -
площадь поперечного сечения канала, а Π - смоченный периметр.
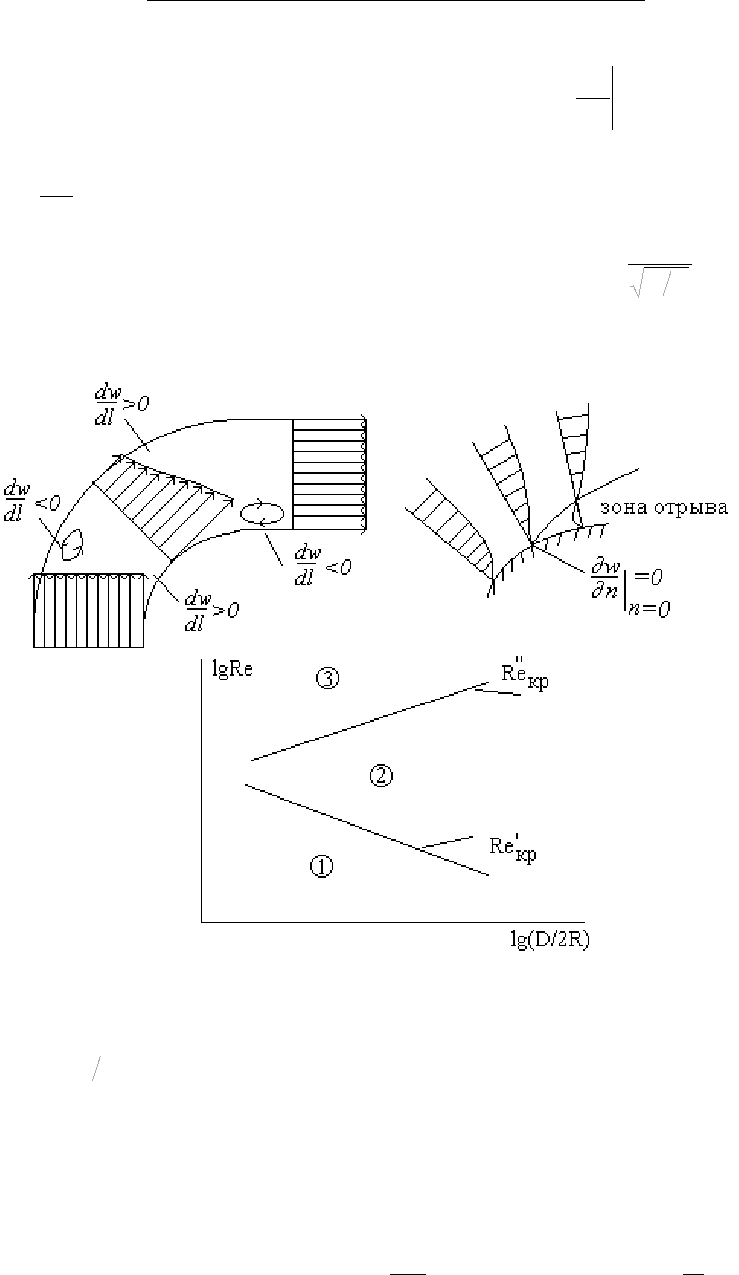
Рис.22.5
254
Теплоотдача в изогнутых и шероховатых трубах
При движении жидкости в изогнутых трубах возможно возникновение зон отрыва
потока, то есть появление так называемых вторичных течений. В точке отрыва
касательное трение на стенке
τ
w
становится равным нулю, т.к. 0
0
=
∂
∂
=n
n
w
.
Условия для отрыва потока создаются при его торможении по какой-либо причине,
т.е. при 0<
∂
∂
l
w
. Вторичная циркуляция возникает при Re ≥
кр
eR
′
. Например, для
течения жидкости в винтовых змеевиках при D/R≥8⋅10
-4
RD
4,16
eR
кр
=
′
, где D-диаметр
трубы, R- радиус змеевика. Отметим, что
кр
eR
′
меньше значения
кр
Re =2300 для гладких
прямых труб. Переход к турбулентному режиму происходит при
кркр
ReeR >
′
′
:
(
)
28,0
кр
218500eR RD=
′′
. Области существования упомянутых режимов течения
представлены на графике: 1- режим без вторичной циркуляции, 2- ламинарный режим с
вторичной циркуляцией, 3- турбулентный режим при наличии вторичной циркуляции.
Вторичные течения приводят к увеличению гидродинамического сопротивления и
росту коэффициента теплоотдачи, для определения которого можно пользоваться
формулой Михеева с поправкой ε
из
из
25,0
43,08,0
Pr
Pr
PrRe023,0Nu
εε
l
w
f
= , где
R
D
8,11
из
+=
ε
. (22.35)
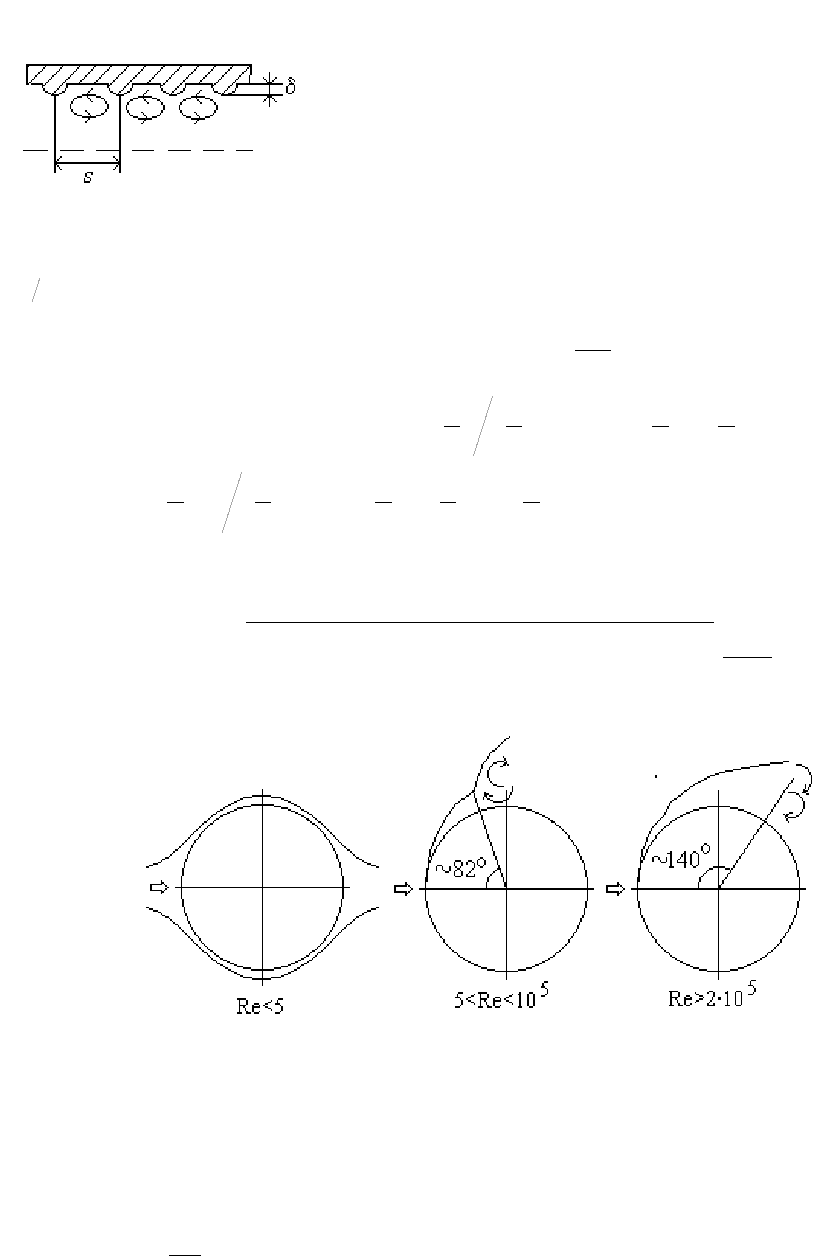
Рис. 22.6
255
Наличие шероховатости приводит к интенсификации теплоотдачи при
турбулентном движении в том случае, когда высота бугорков шероховатости больше
толщины ламинарного подслоя и появляются отрывные зоны (см.рис.22.7).
При ламинарном режиме течения увеличение
интенсивности теплоотдачи обусловлено увеличением
поверхности теплообмена за счет шероховатости.
Шероховатость может увеличивать коэффициент
теплоотдачи в 2...3 раза по сравнению с гладкой
поверхностью. Однако при слишком больших бугорках
возможно образование за ними застойных зон, что может
даже уменьшить α. Следовательно, существует
оптимальное соотношение между шагом s и высотой
бугорков шероховатости
δ
. Исследования показали, что
(
)
14...12
опт
=
δ
s . Для шероховатых труб применяется формула
ш
25,0
47,00,8
Pr
Pr
Pr0,023ReNu
ε
=
w
f
,
где
=
опт
ш
85,0exp
δδ
ε
ss
при
опт
<
δδ
ss
,
=
δδ
ε
ss
опт
ш
85,0exp при
опт
>
δδ
ss
, 13
опт
=
δ
s
, Pr=1...80.
Теплоотдача при поперечном обтекании труб
Плавное, безотрывное обтекание трубы имеет место при 5Re ≤=
∞
∞
ν
Dw
. При 5Re
>
пограничный слой отрывается от поверхно-
Рис.22.8
сти, причем с ростом числа Рейнольдса частота отрыва вихрей f возрастает примерно до
Re=10
3
, после чего становится почти постоянной величиной, характеризуемой числом
Струхаля
∞
=
w
fD
Sh =0,2, где f - частота отрыва вихрей, 1/c.
Рис.22.7
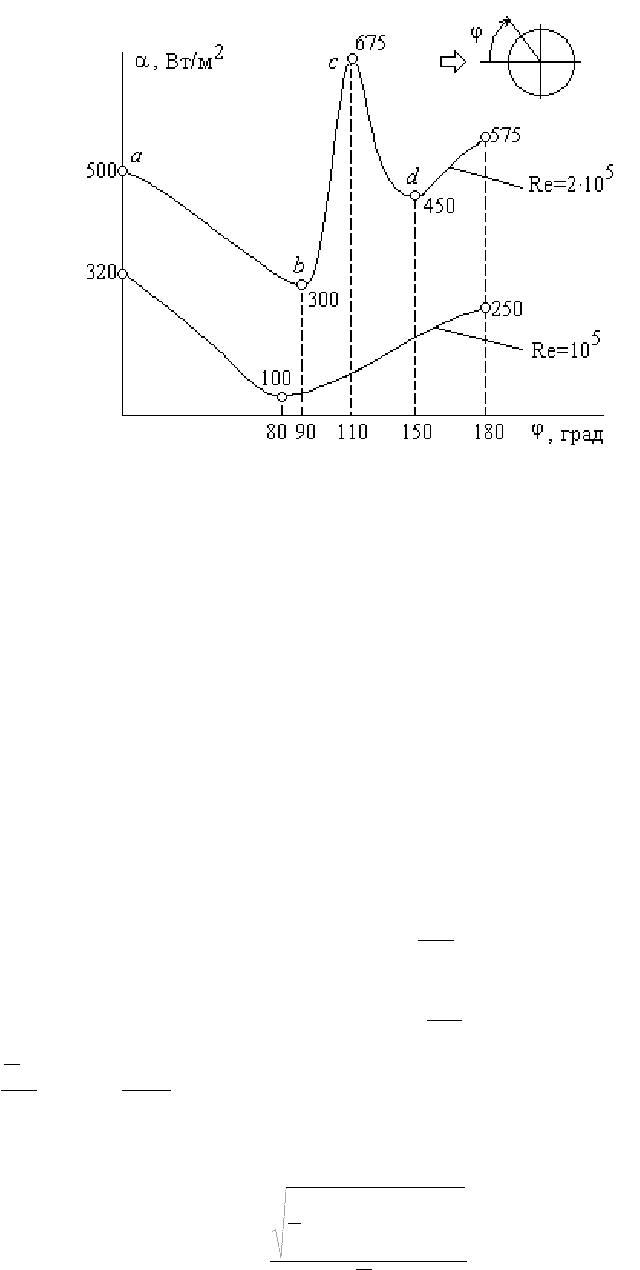
256
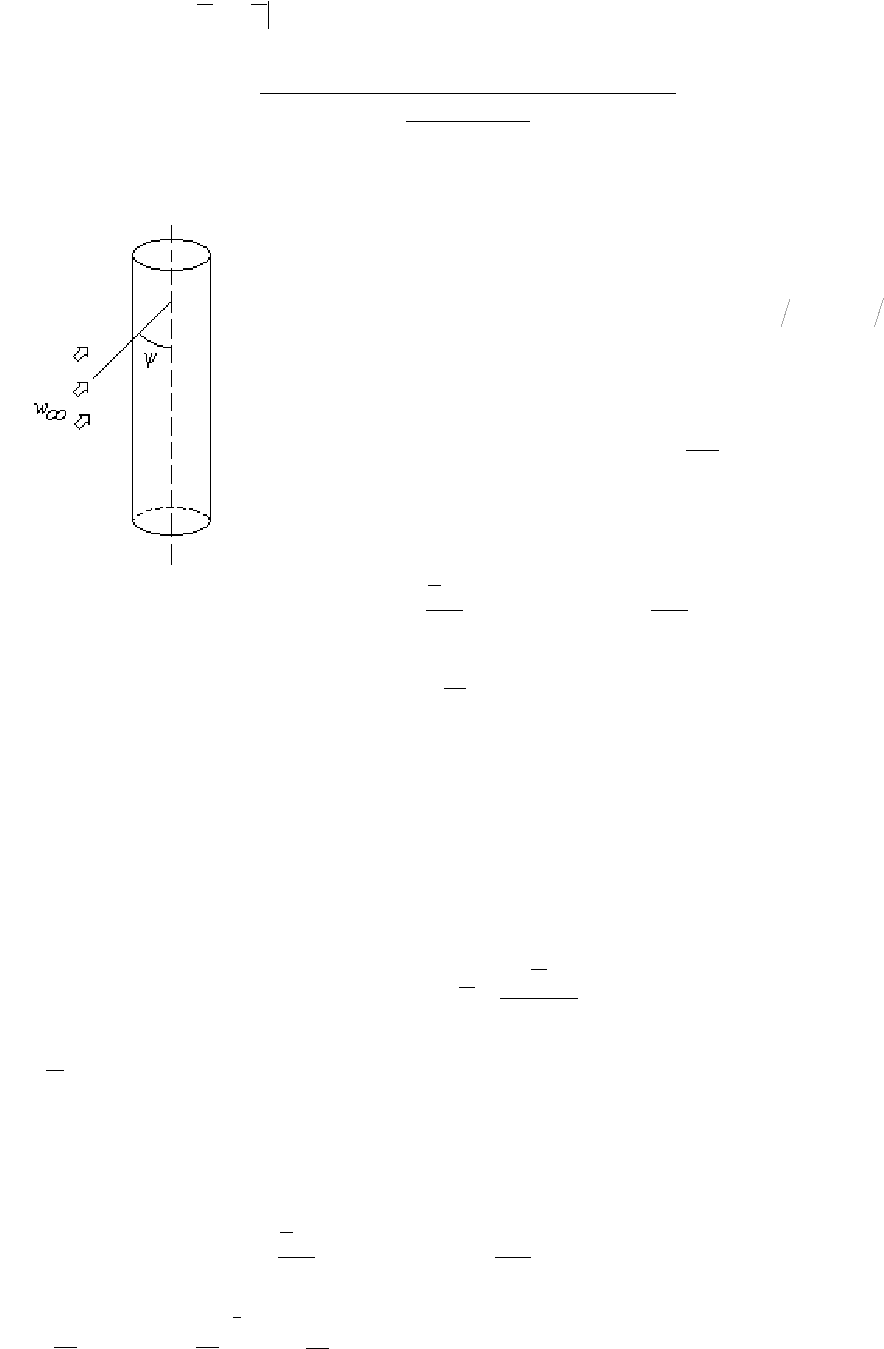
Рис.22.9
Рассмотрим характер изменения локального коэффициента теплоотдачи при
поперечном обтекании цилиндра (Re=2⋅10
5
), рис.22.9. На участке
ab
имеет место
ламинарный погранслой, из-за роста его толщины
α
падает. Участок bc - процесс перехода
к турбулентному режиму, что сопровождается интенсификацией теплоотдачи. На участке
cd с ростом толщины уже турбулентного пограничного слоя
α
снова начинает
уменьшаться. В точке d поток отрывается от поверхности, погранслой разрушается, что
приводит к увеличению коэффициента теплоотдачи. Из рисунка видно, что при Re=10
5
зависимость коэффициента теплоотдачи от угла несколько иная: вначале α падает из-за
роста толщины ламинарного пограничного слоя, а затем растет в зоне отрывного течения.
В результате исследований теплоотдачи при поперечном обтекании одиночных
цилиндров были получены следующие критериальные уравнения:
25,0
38,05,0
Pr
Pr
PrRe5,0Nu
=
w
f
, 1000...5Re
=
, (22.36)
25,0
38,06,0
Pr
Pr
PrRe25,0Nu
=
w
f
,
53
102...10Re ⋅= , (22.37)
∞
=
λ
α
D
Nu
где
;
∞
∞
=
ν
Dw
Re .
Теплоотдача
при
поперечном
обтекании
труб
зависит
от
степени
турбулентности
набегающего
потока
,
под
которой
понимают
отношение
∞
′
+
′
+
′
=
w
www
zyx
__
2
__
2
__
2
3
1
Tu .
При
и14,0Tu
≤
42
10...10TuRe = справедлива формула
(
)
(
)
2,0
0турб
TuRe09,01NuNu += , (22.38)
где Nu
0
- число Нуссельта, определенное по формуле (22.37).
257
Если поток обтекает трубу не по нормали, а под каким-то углом (рис.22.10), то
(
)
ψαα
ψ
ψ
2
90
cos54,01 −=
°=
,
при
°
°
=
90...30
ψ
. (22.39)
Теплоотдача
при
поперечном
обтекании
пучков
труб
Большинство
теплообменных
аппаратов
состоят
из
пучков
труб
(
оребренных
или
гладких
),
поэтому
рассмотрим
особенности
теплообмена
при
внешнем
обтекании
пучков
труб
потоком
.
Применяются
два
основных
типа
пучков
:
коридорные
и
шахматные
.
Характерными
геометрическими
параметрами
являются
относительные
шаги
между
осями
труб
ds
1
и
ds
2
.
В
коридорном
пучке
(
рис
.22.11)
максимальное
значение
локального
коэффициента
теплоотдачи
достигается
при
угле
ϕ=50
0
.
Переход
к
турбулентному
течению
происходит
при
5
ђр
10Re ≈
,
ν
wd
=Re ,
где
w
-
скорость
в
самом
узком
сечении
пучка
.
При
53
..10.10=Re
справедлива
формула
is
f
d
εε
Pr
Pr
PrRe26,0
α
Nu
25,0
w
0,330,65
==
λ
, (22.40)
где
15,0
2
s
−
=
d
s
ε
-
коэффициент
влияния
шага
вдоль
потока
,
коэффициент
i
ε
учитывает
номер
ряда
в
пучке
.
С
увеличением
номера
ряда
i
коэффициент
теплоотдачи
возрастает
,
так
как
первые
ряды
действуют
как
турбулизаторы
и
увеличивают
интенсивность
теплообмена
и
максимальное
значение
α
практически
достигается
уже
к
третьему
ряду
(
см
.
рис
.22.12).
Детальное
изучение
течения
показывает
,
что
90%
стабилизация
потока
происходит
после
4-
го
ряда
и
полностью
завершается
после
14-
го
ряда
.
Для
определения
коэффициента
теплоотдачи
всего
пучка
в
целом
производится
осреднение
по
всем
рядам
:
∑
∑
=
i
ii
F
F
α
α
, (22.41)
где
i
α
,
i
F
-
соответственно
средний
коэффициент
теплоотдачи
и
суммарная
поверхность
трубок
i
-
го
ряда
.
Число
Рейнольдса
подсчитывается
по
скорости
в
наиболее
сжатом
сечении
пучка
.
Для
шахматных
пучков
(
рис
.22.13)
применяется
та
же
формула
,
но
с
другими
постоянными
коэффициентами
:
is
w
f
d
εε
Pr
Pr
PrRe41,0
α
Nu
25,0
0,330,6
==
λ
,
53
..10.10=Re , (22.42)
при
6
1
2
1
s
2
1
2
=<
s
s
s
s
ε
,
при
12,1
ε
2
2
1
=≥
s
s
s
.
Рис.22.10
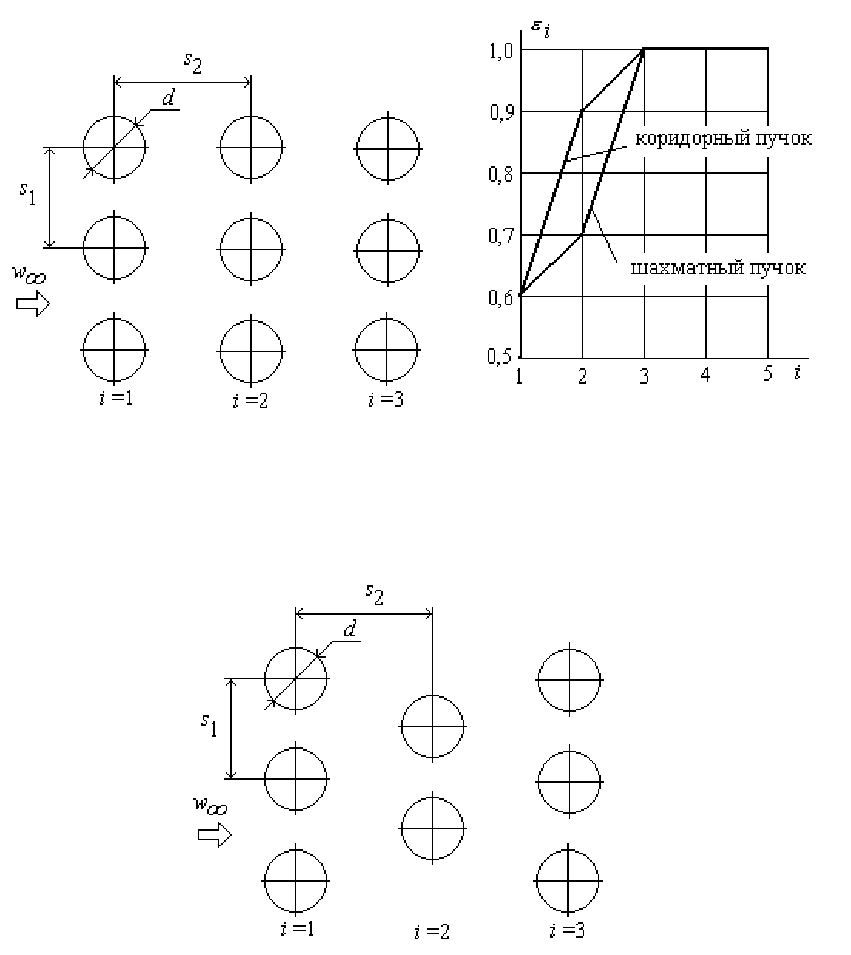
258
В
отличие
от
коридорных
,
в
шахматных
пучках
максимальный
локальный
коэффици
-
ент
теплоотдачи
имеет
место
при
ϕ=0.
Рис
.22.12
Рис
.22.11
Рис
.22.13
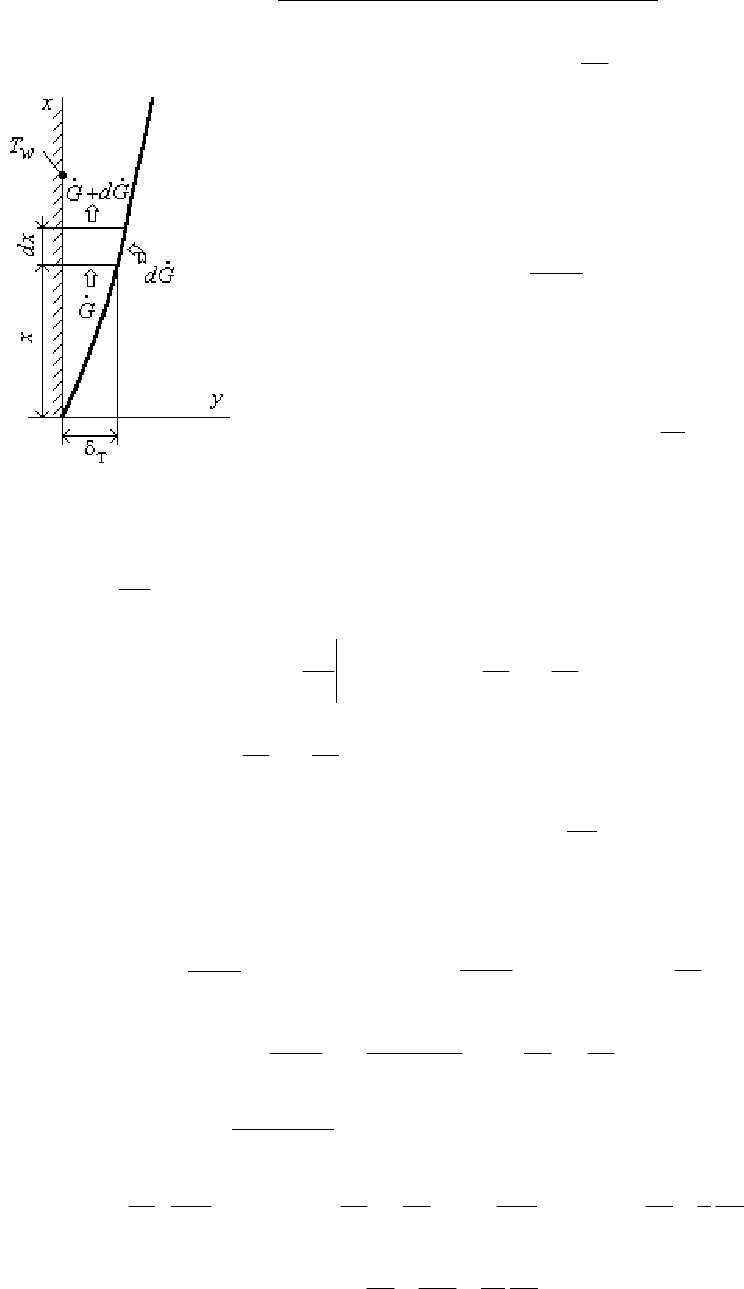
259
23. Теплоотдача при свободном движении жидкости
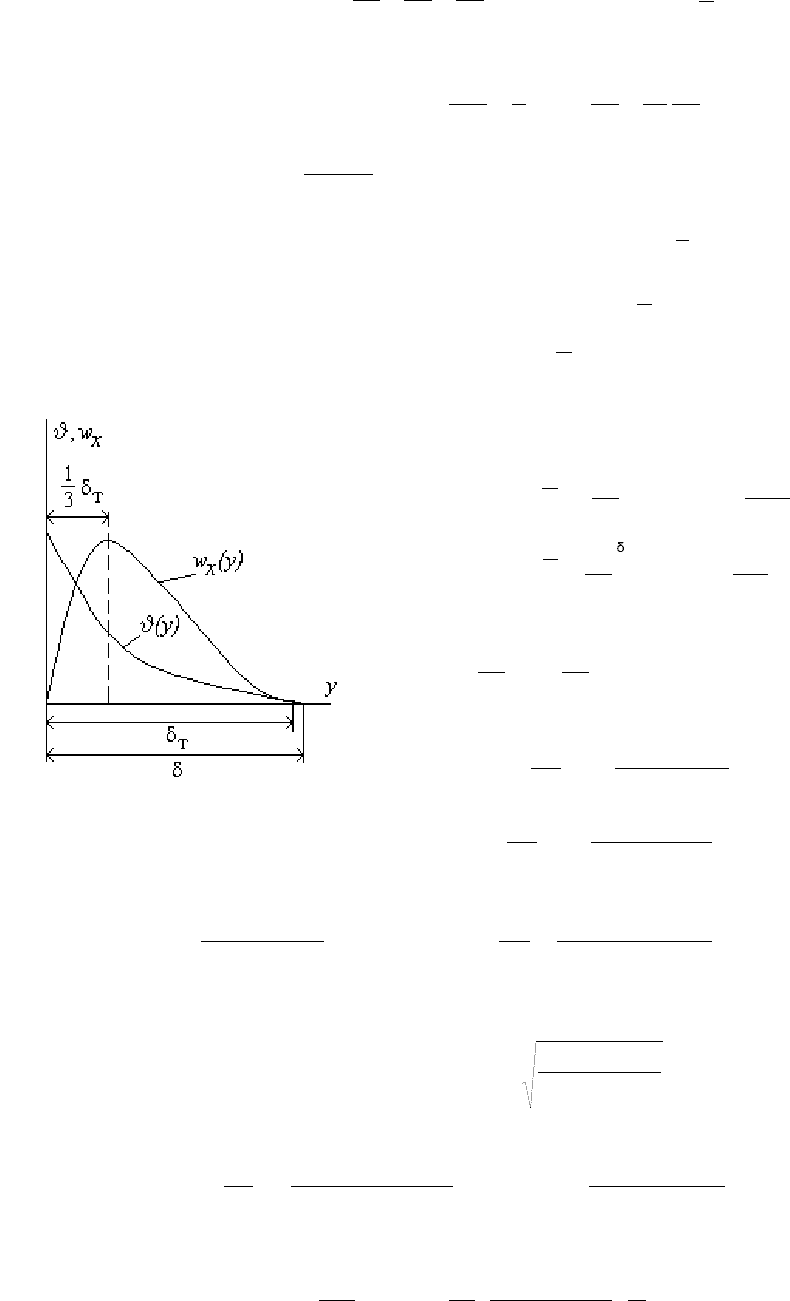
Теплоотдача от вертикальной стенки
Рассмотрим ламинарный пограничный слой у вертикальной пластины (рис.23.1)
при условиях
0 ;const ==
dx
dp
T
w
.
Теплофизические
свойст
-
ва
жидкости
будем
считать
постоянными
за
исключением
плотности
,
которая
зависит
от
температуры
:
(
)
βϑρρ
−=
∞
1
,
∞
−= TT
ϑ
.
Считая
,
кроме
того
,
что
силы
инерции
пренебрежимо
малы
,
т
.
е
.
преобладают
подъемные
и
вязкостные
силы
,
из
уравнения
движения
получим
:
( )
0
2
2
=−+
∞
ρρµ
g
dy
wd
x
.
(23.1)
Экспериментальные
исследования
показали
,
что
закон
изме
-
нения
избыточной
температуры
в
тепловом
пограничном
слое
описывается
выражением
2
т
1
−=
δ
ϑϑ
y
w
. (
а
)
Найдем
связь
между
толщиной
пограничного
слоя
и
коэф
-
фициентом
теплоотдачи
,
для
чего
воспользуемся
граничны
-
ми
условиями
III
рода
:
0=y
wx
dy
d
−=
ϑ
λϑα
.
С
учетом
(
а
)
имеем
:
0=
TT
0
1
12
y
w
y
y
dy
d
−
−=
=
δδ
ϑ
ϑ
,
тогда
0=
TT
1
12
α
y
ww
y
−
−=
ϑ
δδ
λϑ
,
следовательно
,
T
2
=
δ
λ
α
x
. (23.2)
При
- = 0
T
∞=
αδ
нет
термического
сопротивления
.
Проинтегрируем
уравнение
движения
(23.1)
с
учетом
(23.2)
и
(
а
):
,0
2
2
=+
∞
ϑβρµ
g
dy
wd
x
,01
2
T
2
2
=
−+
∞
δ
βϑρµ
y
g
dy
wd
w
x
+−−=
∞
2
TT
2
2
21
δδµ
ϑβρ
yy
g
dy
wd
wx
.
Введем
обозначение
A
g
w
=
∞
µ
ϑ
β
ρ
,
разделим
переменные
и
дважды
проинтегрируем
:
+−−=
2
TT
21
δδ
yy
A
dy
dw
dy
d
x
,
1
2
T
3
T
2
3
1
C
yy
yA
dy
dw
x
+
+−−=
δδ
,
+
12
1
32
21
2
T
4
T
32
CyC
yyy
Aw
x
+
+−−=
δδ
. (b)
Рис
.23.1
260
Найдем
постоянные
интегрирования
.
При
(
)
0 0:0=
2
=⇒= Cywy
x
,
при
0)(:
==
Т
x
Т
wy
δδ
,
тогда
0
1232
T1
2
T
2
T
2
T
=+
+−−
δ
δδδ
CA ,
⇒
T1
4
1
δ
AC =
.
Подставляя
С
1
в
(b),
получим
закон
изменения
скорости
по
толщине
теплового
пограничного
слоя
( )
12
1
24
1
3
2
T
42
T
T
3
−−+=
δ
δ
δ
yy
y
y
Ayw
x
. (23.3)
Используя
(23.3)
и
условие
(
)
0
=
dy
ydw
x
,
можно
найти
расстояние
от
стенки
,
на
котором
скорость
в
пограничном
слое
максимальна
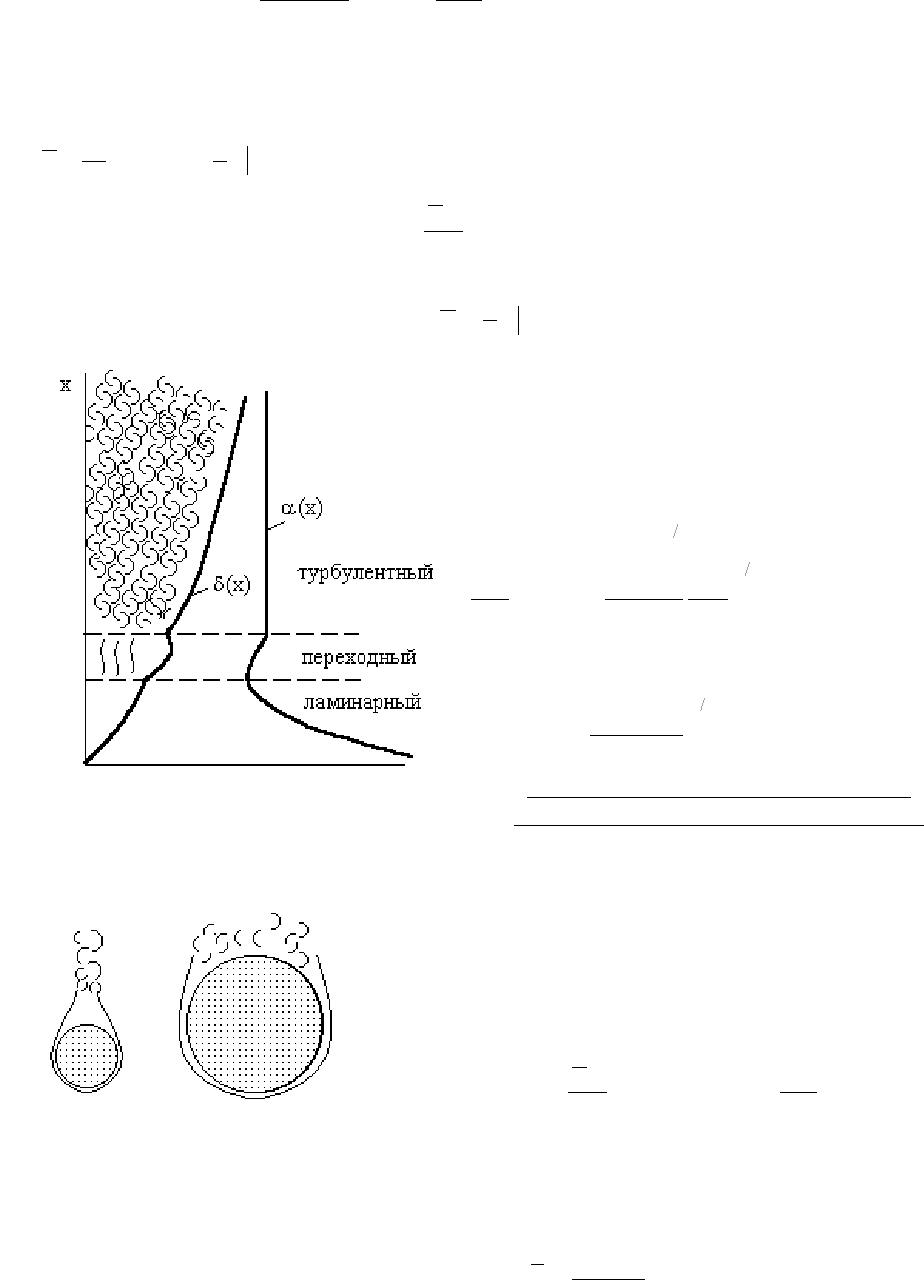
:
maxxx
ww
=
при
у
≈
T
3
1
δ
(
рис
.23.2).
Напишем
уравнение
теплового
баланса
для
выделенного
неподвижного
элемента
:
Gdcdx
pwx
&
1
ϑϑα
=⋅⋅
, (
с
)
(
)
1
T
⋅
∞
δρ
w=dGd
&
, (d)
Средние по толщине пограничного слоя скорость и
температуру найдем, подставляя в интегралы выра-
жения (23.3) и (а):
( )
∫
==
T
0
2
T
T
40
1
δ
δ
δ
A
dyyww
xx
, (e
)
( )
3
1
T
0
T
w
dyy
ϑ
ϑ
δ
ϑ
==
∫
. (f
)
Подставим (d),(e) и (f) в (с):
3
Т
40
3
=
α
δρ
ϑ
ϑ
d
A
cdx
p
w
wx
∞
, а с учетом (23.2) и выраже-
ния для А
( )
3
T
2
T
120
=
2
δ
µ
βϑρ
δ
λ
d
gc
dx
wp ∞
,
T
2
T
w
2
T
3
120
=
2
δδ
µ
βϑρ
δ
λ
d
gc
dx
p ∞
.
Разделим переменные и проинтегрируем:
T
3
T
2
=
80
δδ
βϑρ
µ
λ
ddx
g c
wp ∞
,
x
gc
p w
2
4
T
80
4
ϑβρ
µλ
δ
∞
=
.
Таким образом, закон изменения толщины теплового пограничного слоя, разви-
вающегося у вертикальной пластины, имеет вид
4
2
T
320
wp
gc
x
ϑβρ
µλ
δ
∞
=
. (23.4)
Определим теперь локальный коэффициент теплоотдачи
25,0
2
3
25,0
2
4
T
x
473,0
320
16
2
=
==
∞∞
x
gc
x
gc
wp wp
µ
βϑρλ
µλ
βϑρλ
δ
λ
α
и
локальное
число
Нуссельта
25,0
2
3
x
473,0
Nu
⋅⋅==
∞
µ
µ
µ
βϑρ
λλ
α
wp
gc
xx
.
Рис
.23.2
261
Учитывая
,
что
=Pr ,
Gr
2
3
x
λ
µ
ν
ϑβ
c
xg
p
w
= ,
получаем
критериальное
уравнение
те
-
плоотдачи
(
)
25,0
xx
PrGr 473,0Nu = . (23.5)
Средний
по
длине
пластины
коэффициент
теплоотдачи
равен
( )
Hx
H
dxx
H
=
==
∫
ααα
3
41
0
,
а
среднее
число
Нуссельта
( )
25,0
__
PrGr63,0Nu ⋅==
λ
α
H
.
В
случае
постоянной
плотности
теплового
потока
на
стенке
q
w
=const:
(
)
25,0
xx
PrGr0,6Nu = ,
Hx=
=
αα
4
5
,
( )
25,0
__
PrGr75,0Nu ⋅= .
Приведенные
формулы
справедливы
в
диапазоне
(Gr⋅Pr)=10
3
...10
9
,
когда
режим
тече
-
ния
является
ламинарным
.
Критическое
значе
-
ние
для
перехода
к
турбулентному
режиму
-
(Gr⋅Pr)
кр
≈6⋅10
10
.
При
турбулентном
режиме
справедливы
следующие
зависимости
:
(
)
31
xx
PrGr0,15Nu ⋅= ,
или
31
2
3
15,0
=
∞
λ
µ
ν
βϑ
λ
λ
α
p
wx
c
xgx
,
откуда
видим
,
что
при
турбулентном
режиме
коэффициент
тепло
-
отдачи
не
зависит
от
координаты
х
:
31
2
15,0
=
∞
λν
µβϑ
λα
pw
x
cg
(
см
.
рис
.23.3).
Теплоотдача
от
горизонтальных
труб
и
проволочек
при
свободной
конвекции
Характер
свободного
движения
около
горя
-
чих
горизонтальных
труб
представлен
на
рис
.23.4.
Чем
больше
диаметр
трубы
,
тем
более
вероятно
разрушение
ламинарного
пограничного
слоя
.
У
труб
малого
диа
-
метра
турбулентное
течение
может
возникать
вдали
от
трубы
.
Средние
коэффициенты
теплоотдачи
при
сво
-
бодной
конвекции
около
горизонтальных
труб
при
Gr⋅Pr=10
3
...10
6
определяются
по
формуле
( )
25,0
25,0
Pr
Pr
PrGr5,0Nu
⋅==
∞
w
d
λ
α
. (23.6)
Около
тонких
проволочек
диаметром
d=0,2...2
мм
об
-
разуется
неподвижная
пленка
нагретой
жидкости
.
Такой
режим
называется
пленочным
,
теплообмен
осуществляется
теплопроводностью
.
При
пленочном
режиме
Gr⋅Pr≤1,
5,0Nu
=
. Определяющей температурой является сред-
няя температура
2
w
TT
T
+
=
∞
.
Рис.23.3
Рис.23.4
