Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.


282
а
ReSc
Sh
St
д
= -
диффузионное
число
Стентона
.
Таким
образом
, (*)
можно
переписать
в
виде
wwсlwD
Dl
lw
al
p
β
ρ
α
ν
νβ
νλ
να
== или, .
В соответствии с аналогией Рейнольдса для пластины т.е.,Pr
2
St
3
2
−
=
f
c
3
2
Pr
2
−
∞∞
==
f
p
c
wwc
β
ρ
α
(26.6)
или для локальных коэффициентов
3
2
Pr
2
βα
−
∞∞
==
f
x
p
x
c
wwc
ρ
. (26.6а)
Таким образом, найдена связь между коэффициентами теплоотдачи, массопереноса
и трения. Определив, например, из опыта гидродинамическую величину c
f
, можно
найти две других.
Тройная аналогия справедлива при обтекании потоком пластины, для труб она полностью
не выполняется, так как течение в трубах не является безградиентным
.0
≠
dx
dp
Тепло- и массоотдача от пластины при ламинарном и турбулентном режимах течения
При обтекании пластины ламинарным потоком справедливы следующие формулы:
33,05,0
PrRe323,0
α
Nu
x
x
x
x
==
λ
,
33,05,0
PrRe646,0Nu =
,
33,05,0
ScRe323,0Sh
x
x
x
D
x
==
β
, (26.7)
33,05,0
ScRe646,0Sh ==
D
l
β
, (26.8)
( )
33,05,0
3
1
д
ScRe
64,4
Sc
x
x
x
==
δ
δ
. (26.9)
При турбулентном режиме течения (Re>10
5
)
33,08,0
ScRe0296,0Sh
x
x
x
D
x
==
β
, (26.10)
33,08,0
ScRe037,0Sh ==
D
l
β
, (26.11)
( )
33,02,0
3
1
тб
д
ScRe
37,0
Sc
x
x
x
==
δ
δ
. (26.12)
Массоперенос в трубах
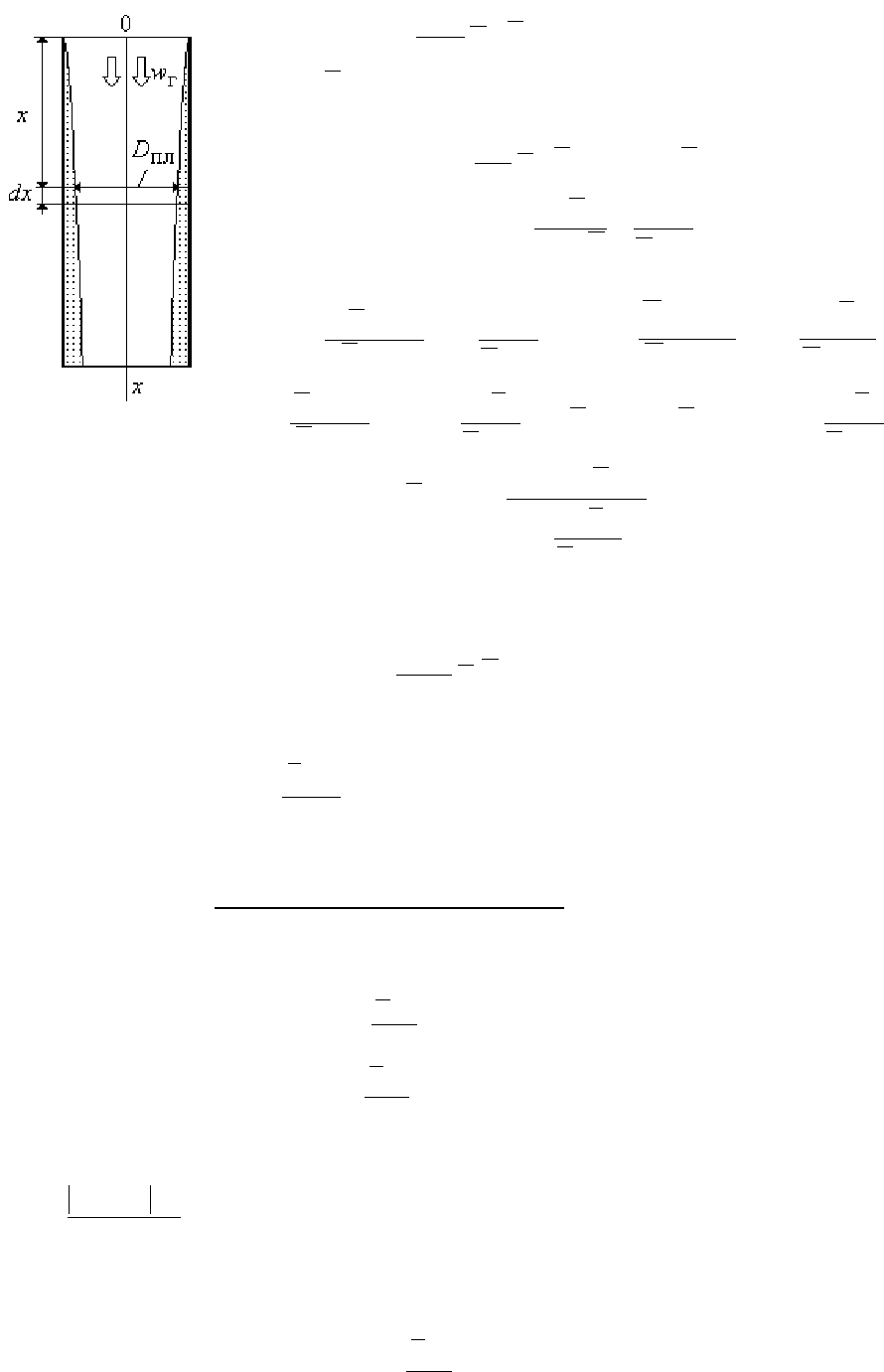
Рассмотрим процесс массопереноса в трубе, в которой движется газ, а по
стенкам течет пленка жидкости (рис.26.4). Так как изменение концентрации
компонента в газе обусловлено потоком массы с элементарной поверхности
пленки, то можно написать
283
dxDjCdw
D
плг
2
пл
4
π
π
= , (26.13)
где С - концентрация компонента, осредненная по сечению.
Далее будем считать, что пленка тонкая D
пл
≈ D
тр
, тогда
( )
dxCCCdw
D
wx
−=
β
г
тр
4
.
Разделим переменные: dx
Dw
CC
Cd
x
w
трг
4
β
=
−
и проинтегрируем:
(
)
∫∫
−=
−
−
l
x
C
C
w
w
dx
Dw
CC
CCd
0
трг
4
2
1
β
,
l
Dw
CC
CC
w
w
трг
1
2
4
ln
β
−=
−
−
,
−=
−
−
l
Dw
CC
CC
w
w
трг
1
2
4
exp
β
,
( )
−−=− l
Dw
CCCC
ww
трг
12
4
exp
β
,
(
)
−
−=
l
Dw
CC
CC
w
w
трг
1
2
4
exp
β
(26.14)
-концентрация паров жидкости на выходе из трубы.
Расход испарившейся жидкости найдем из формулы
2г
2
тр
2
4
Cw
D
G
π
=
&
, кг/с.
Средний коэффициент массоотдачи можно определить из критериального уравнения,
полученного Шервудом
n
D
D
ScRe023,0Sh
83,0
тр
==
β
,
где n = 0,44 при Sc = 0,6...2,5 и n = 0,33 при Sc = 10
3
...2⋅10
3
.
Тепло-и массоперенос от капель
Существует значительное число уравнений, позволяющих определить тепло-и
массоперенос от капель. Наиболее часто в расчетной практике используют
уравнения вида:
33,0
г
5,0
к
г
к
PrRe6,02Nu +==
λ
α
D
, (26.15)
33,05,0
к
к
ScRe6,02Sh +==
D
D
β
, (26.16)
где второе слагаемое в правой части уравнений называется ветровым множителем,
который учитывает конвективный тепло - и массоперенос,
г
кг
к
ν
Re
Dww
к
−
= , 0 < Re
к
≤ 200.
Если рассматривать процессы на чисто молекулярном уровне, то
Nu=2, Sh=2.
Вырубов, исследуя испарение капель бензина в воздушном потоке, получил
критериальное уравнение
0,5
к
к
Re52,0Sh ==
D
D
β
, (26.17)
Рис.26.4

284
которое справедливо в диапазоне 300 ≤ Re
к
≤ 500.
Р.Д Ингево., исследовавший испарение с пробковых шаров, пропитанных водой,
ацетоном и четыреххлористым углеродом,
получил уравнение
+
∆
=
5.0
.
6.0
.
)()(Re303.02
пара
возд
ш
возд
Sc
rD
T
j
λ
λλ
,
с
м
кг
2
(26.17a
)
где
∆
T = T
мокр.терм.
-T
возд.
;
Re
= w
возд.
D
ш
./
ν
возд.
= (1,7÷6)10
3
.
27. Лучистый теплообмен
Общие положения
В основе теории теплового излучения лежит как волновая, так и корпускулярная
теория. Согласно первой тепловая энергия распространяется со скоростью света
ν
λ
=
c
,
где
λ
-длина волны, ν-частота колебаний, а по второй - поглощение и выделение энергии
происходит порциями - фотонами. Энергия фотона e = hν , где h - постоянная Планка.
При нагреве тела электроны переходят на более высокие энергетические уровни.
Возвращаясь на более низкий уровень электрон испускает фотон, энергия которого
равна разности энергий возбужденного и равновесного состояний. Переход электронов
на разные энергетические уровни приводит к распределению энергии фотонов,
покидающих поверхность тела, по спектру частот. Энергия фотонов, покидающих
поверхность тела, называется тепловым излучением, которое зависит только от
температуры тела. Тепловое излучение находится в диапазоне длин волн λ = 10
-
7
...10
-4
м. Видимый спектр излучения лежит в диапазоне “10)6,78,3(
7−
⋅
K
.
Основные законы излучения
В 1900 году Макс Планк установил зависимость плотности потока
монохроматического (спектрального) излучения абсолютно черного тела от температуры
и длины волны
−
=
1e
T
c
5
1
o
2
λ
λ
λ
C
E Вт/м
3
,
(27.1)
где
16
1
107418,3
−
⋅=С Вт⋅м
2
- первая постоянная излучения,
2
2
104388,1
−
⋅=С м⋅К - вторая
постоянная излучения.
Для коротких длин волн, когда 1e
T
c
2
>>
λ
, получаем формулу Вина:
=
T
C
C
E
λ
λ
λ
2
e
5
1
o
. (27.2)
Если 1e
2
≈
T
C
λ
, то
K++≈
Т
1e
2
2
λ
λ
C
T
C
и подставляя в (27.1), получим формулу Релея-
Джинса
2
4
1
o
C
ТC
E
λ
λ
= .
(27.3)
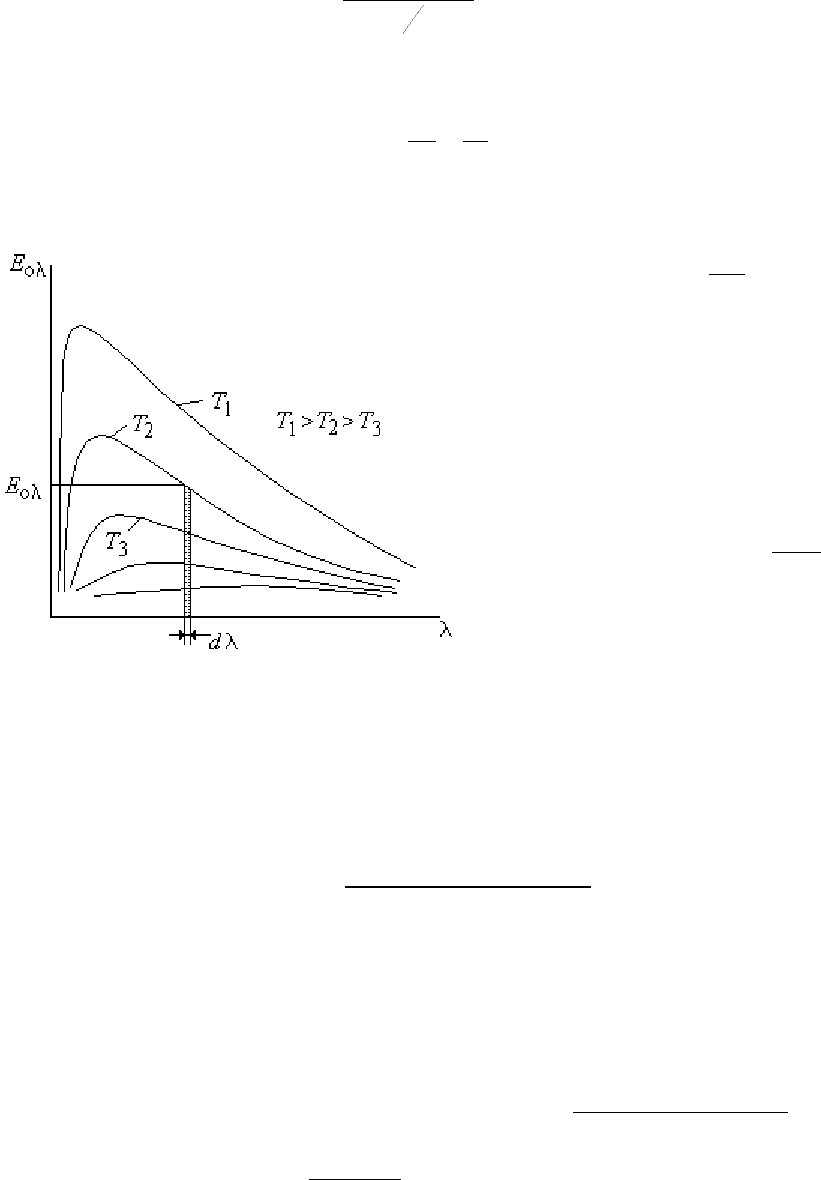
Выделим под кривой E
0λ
=f(T,λ) элементарную площадку
λ
λ
dEdE
00
=
(рис.27.1) и
проинтегрируем полученное выражение в пределах от λ=0 до λ=∞, тогда
285
∫
∞=
=
−
=
λ
λ
λ
σλ
λ
0
4
0
5
1
0
=
1e
E
2
Td
C
T
C
(27.4)
-закон Стефана-Больцмана, где E
0
- плотность потока интегрального излучения
абсолютно черного тела, Вт/ м
2
,
8
1
4
2
0
1067,5
15
−
⋅=
=
C
C
π
σ
, Вт/(м
2
К
4
) - постоянная
Стефана-Больцмана.
Часто закон записывают в виде
4
00
100
=
T
CE , (27.5)
где
0
C
- коэффициент излучения
абсолютно черного тела, 67,5
0
=C
Вт/(м
2
К
4
).
Абсолютно черное тело - это тело,
которое при данной температуре
излучает или поглощает максимум
лучистой энергии.
Взяв производную
λ
λ
d
dE
0
и
приравняв ее нулю, получим закон
смещения Вина:
-3
max
102,898= ⋅Т
λ
м⋅
К , (27.6)
который показывает, что максимум
плотности монохроматического
излучения с увеличением температуры смещается в сторону коротких длин волн. Если
λ
max
из (27.6) подставить в (27.1) , то получим :
55
max0
10287,1 TE
−
⋅=
λ
Вт/ м
3
.
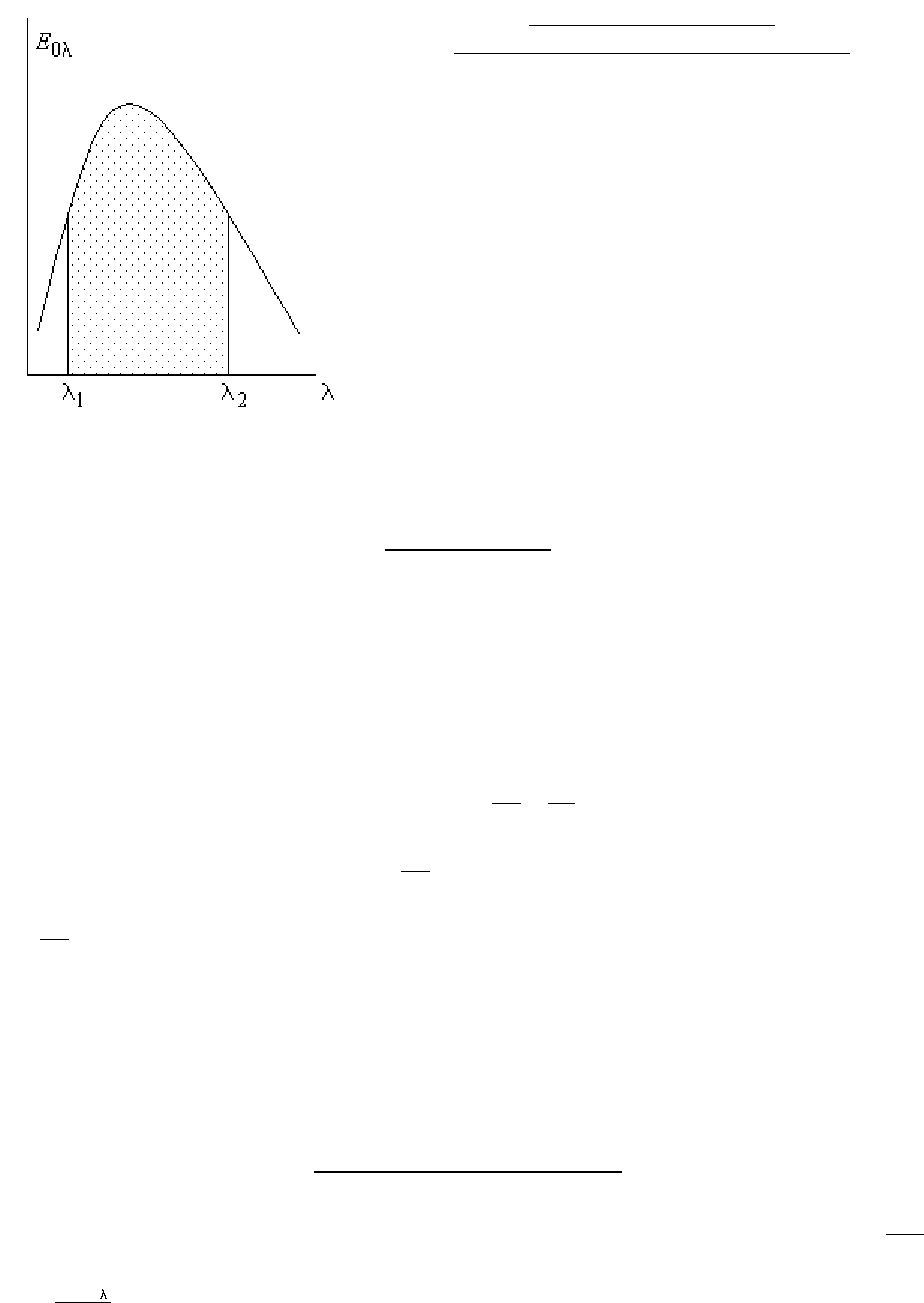
Радиационные функции
Часто необходимо определить энергию излучения черной поверхности в заданном
диапазоне длин волн. Так, в диапазоне от 0 до λ
1
можно
написать
( )
∫
=−
1
0
010
0
λ
λ
λλ
dEE
, в диапазоне от 0 до λ
2
будем иметь
( )
∫
=−
2
0
020
0
λ
λ
λλ
dEE
.
Вычитая из одной функции другую, найдем искомую энергию излучения. Если
эту разность разделить на σ
0
T
4
, то получим долю энергии, которую излучает
абсолютно черное тело в данном диапазоне длин волн
(
)
(
)
4
0
1020
00
T
EE
σ
λ
λ
−
−
−
. Существуют
таблицы для функций вида
(
)
4
0
0
0
T
E
σ
λ
−
, которые называются радиационными функциями
черного тела.
Рис. 27.1
286
Радиационные свойства
Интегральные радиационные свойства
(энергия осреднена по всем
длинам волн)
Лучистую энергию, падающую на тело,
можно представить в виде трех составляющих:
отраженной, поглощенной и пропущенной телом
энергии
E
пад
= E
отр
+ E
погл
+ E
пр
. (27.7)
Разделив (27.7) на E
пад
, получим
1 = R + A + D ,
где R- коэффициент, характеризующий
отражательную способность тела, А- коэффициент,
характеризующий поглощательную способность тела,
D - коэффициент, характеризующий диатермичность
тела. Для абсолютно черного тела R = D = 0 , A = 1;
для абсолютно прозрачного тела А= R= 0, D = 1; для
зеркальной поверхности A = D = 0 , R = 1.
Закон Кирхгофа
Поместим в изотермическую полость тело с поглощательной способностью А
1
.
После наступления термодинамического равновесия между телом и оболочкой тело
поглотит энергию
пад
1
погл
1
EАE = (а) . Удалим первое тело и поместим второе тех же
размеров и формы, тогда
пад
2
погл
2
EАE = (б). Но при термодинамическом равновесии
энергия поглощенного излучения равна энергии испущенного излучения,
следовательно, Е
погл
1
= Е
1 ,
а Е
погл
2
= Е
2
. Теперь (а) и (б) можно переписать так:
пад
11
EАE = (в),
пад
22
EАE = (д) .
Разделим (в) на (д):
2
1
2
1
А
А
E
E
= . (27.8)
Будем считать, что
1
2
=А
, тогда
1
0
1
А
E
E
= , но по определению степень черноты
0
1
E
E
=
ε
есть отношение лучистой энергии, испускаемой серым телом к лучистой
энергии, излучаемой черным телом при той же температуре с единицы
поверхности.
Таким образом,
11
ε
=А
, (27.9)
то есть при тепловом равновесии поглощательная способность тела равна
излучательной - закон Кирхгофа.
Монохроматические свойства
Излучательная и поглощательная способность тел зависит от длины волны
излучения, поэтому вводят такие понятия, как спектральные свойства :
λ
λ
λ
ε
0
E
E
= ,
λ
λ
пад
погл
E
E
А =
. Свяжем между собой интегральные и спектральные свойства
рис.27.2
287
∫
∫
∫
∞=
=
∞=
=
∞=
=
==
λ
λ
λλ
λ
λ
λ
λ
λ
λλ
λε
σ
λ
λε
ε
0
0
4
0
0
0
0
0
1
dE
Т
dE
dE
. (27.10)
Из (27.10) видно, что степень черноты зависит только от физических свойств излучателя.
Поглощательная же способность тела зависит как от поглощательной способности самого
тела, так и от характеристик тел, от которых исходит лучистая энергия:
∫
∫
∞
=
∞
=
0
пад
=
0
пад
=
λ
λ
λ
λ
λλ
λ
λ
dE
dEА
А . (27.11)
Для того чтобы упростить расчеты, вводят понятие серого тела, т.е. полагают
λλλλ
εεε
== , ,const и A=AА . Для серых тел
А
=
ε
даже в том случае, если тела не
находятся в тепловом равновесии. При этом считают, что у серых тел D = 0 .
Направленные радиационные свойства
Исследования показали, что радиационные свойства зависят не только от длины
волны и состояния поверхности излучателя и приемника, но и от направления
излучения. У металлов наибольшая излучательная способность имеет место при
больших углах
θ
(угол между нормалью к поверхности и направлением излучения), а
у диэлектриков - при
0
→
θ
. Для рассмотрения направленных излучательных свойств
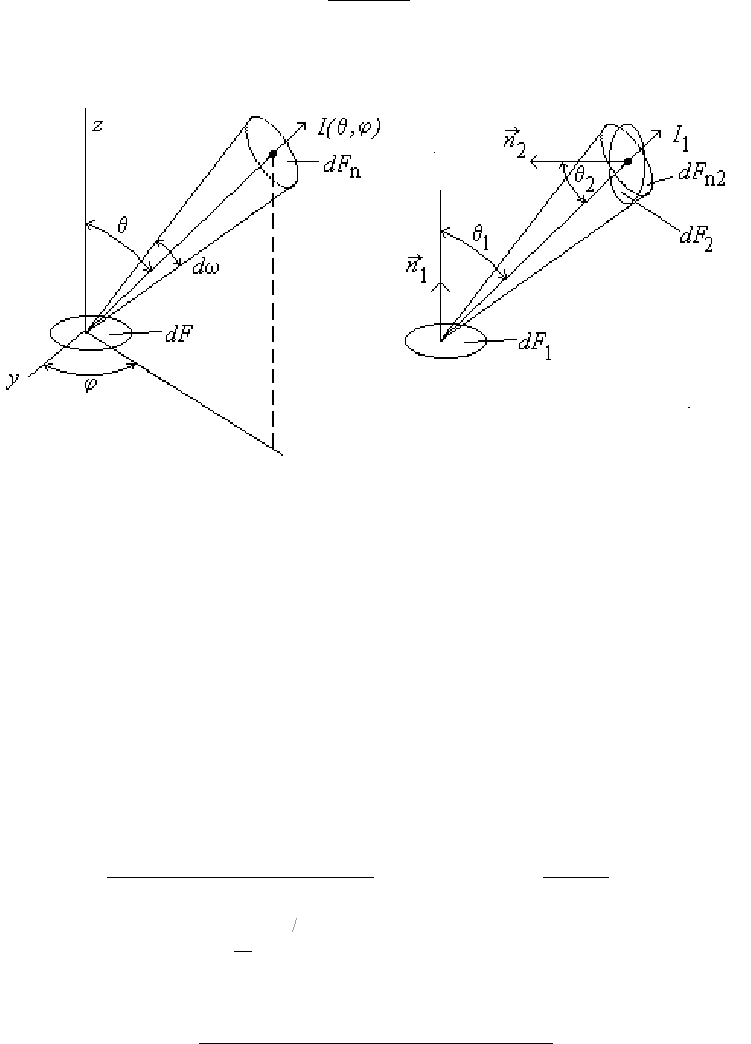
вводят понятие телесного угла и интенсивности излучения (яркости).
Телесный угол
2
n
r
dF
d =
ω
(27.12)
есть отношение площади элементарной площадки dF
n
, расположенной
перпендикулярно радиусу, к радиусу в квадрате и измеряется в стерадианах (ср).
Рис.27.3
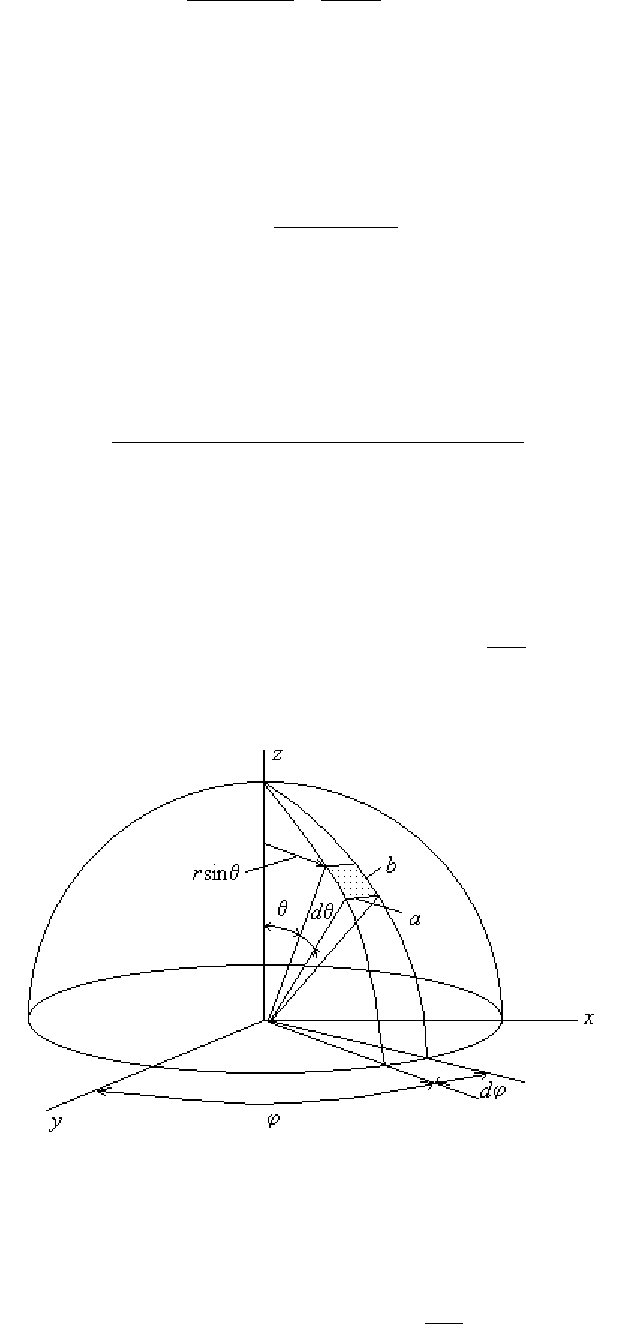
Число стерадиан в угле, ограниченном замкнутой поверхностью, может быть
найдено путем интегрирования (27.12). Так, например, для сферы можно написать
(
см. рис.27.3):
θϕθ
drdrabdF ⋅⋅⋅= sin=
n
, но
θϕθω
dd
r
dF
d sin=
2
n
= ,
288
тогда
∫ ∫ ∫
=
⋅⋅=
сф
2
0= 0
сф
4=sin=
π
ϕ
π
θ
πθϕθωω
ddd .
Лучистая энергия, излучаемая с единичной поверхности, перпендикулярной к
направлению излучения, в единицу времени в пределах единичного элементарного
телесного угла (рис.27.4), называется интенсивностью излучения
( )
θω
ϕθ
cos
,
d
dE
I =
,
Вт/(м
2
ср). (27.13)
Из (27.13) можно получить
(
)
θωϕθ
cos,= dIdE
. (27.14)
Рис.27.4
Проинтегрируем уравнение (27.14) по полусфере, то есть определим количество лучистой
энергии, которое отдает плоская поверхность окружающей среде, полагая поверхность
диффузионной (излучает с постоянной интенсивностью по всем углам), то есть
I(
θ
,
ϕ
) = const
( )
.cossin
0 0
Idd,IE
2 /2
πθϕθθϕθ
π
ϕ
π
θ
==
∫ ∫
= =
(27.15)
Диффузионным является и черное тело
E
0
=
π
I
0
. (27.16)
Интегральную степень черноты теперь можно записать в виде
( )
но,
cossin,
0
2
0
2/
0
I
ddI
π
θϕθθϕθ
ε
π
ϕ
π
θ
∫ ∫
= =
=
(
)
тогда,
,
),(
0
I
I
ϕ
θ
ϕθε
=
( )
.cossin,
1
2
0
2
0
∫ ∫
= =
=
π
ϕ
π
θ
θϕθθϕθε
π
ε
dd (27.17)
Угловой коэффициент излучения
Рассмотрим два тела, обменивающиеся лучистой энергией. Под угловым
коэффициентом излучения понимают отношение лучистой энергии, которая дошла до
второго тела от первого, ко всей энергии, излучаемой первым телом в полупространство
(
в полусферу).
Для элементарных площадок, где dF
1
- излучающая, а dF
2
- приемная, угловой
коэффициент при I
1
=const

289
2
221
1
111
1
coscos
cos
21
r
dF
I
dI
I
dE
dFdF
π
θθ
π
θ
ω
π
ϕ
===
→
. (27.18)
Для диффузионных тел конечных размеров можно написать:
∫ ∫
=
→
1 2
2
2112
1
21
coscos1
F F
r
dFdF
F
π
θ
θ
ϕ
. (27.19)
Формула (27.19) показывает, какая доля лучистой энергии тела 1, излучающего в
полусферу, падает на тело 2.
Если выполнить аналогичные рассуждения для случая, когда излучающей будет вторая
площадка, то
21
2
12
2
12
1 2
coscos1
dFdF
rF
F F
∫ ∫
=
→
π
θ
θ
ϕ
. (27.20)
Сравнивая (27.19) и
(27.20), можно получить условие взаимности
,
212121
FF
→→
=
ϕϕ
(27.21)
которое применимо для любых двух тел в пространстве, обменивающихся лучистой
энергией. Вводя понятие “взаимные поверхности излучения“ H, можно написать:
.,
2121212121
FHFH
→→→→
==
ϕϕ
Следовательно, .
1221 →→
= HH
Получим выражение для условия замкнутости. Рассмотрим замкнутую систему,
состоящую из трех поверхностей. Будем считать, что первая поверхность является
излучателем, тогда ее энергию излучения можно представить в виде
,
1131211 →→→
++= EEEE
где Е
1-2
- энергия излучения падающая на вторую поверхность и т. д. Разделив все
члены на Е
1,
получим
.1
113121 →→→
++=
ϕϕϕ
Если излучатель плоский или выпуклый, то в этом случае говорят, что тело “не видит”
себя и тогда ϕ
1-1
= 0.
Для замкнутой системы, состоящей из n поверхностей, будем иметь
.1
1
=
∑
=
→
n
j
ji
ϕ
(27.22)
Условия взаимности и замкнутости позволяют решать задачи лучистого
теплообмена для тел, произвольно расположенных в пространстве.
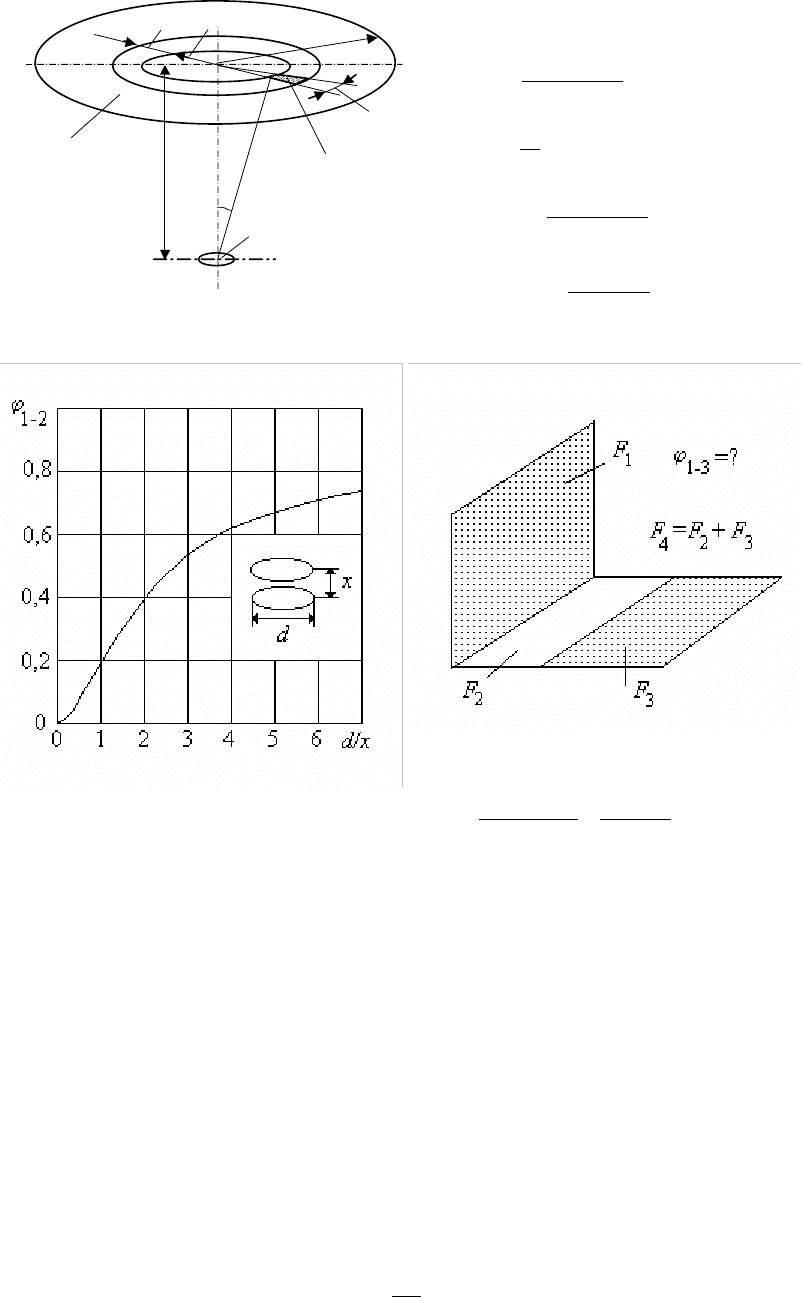
Методы определения угловых коэффициентов
1. Аналитический метод.
В этом случае необходимо взять интегралы (27.19) и (27.20). Определим
21−
ϕ
. В
качестве примера рассмотрим лучистый теплообмен между двумя параллельными
дисками, имеющими общую ось.
290
Применяя формулу (27.19) к рис.27.5 и полагая
F
1
<<
F
2
, можно написать
∫
=
−
2
2
2
2
21
F
r
dFCos
π
θ
ϕ
, но
ρϕρ
ddFd =
2
, а
r
r
Cos
0
=
θ
, тогда
∫∫
=
−
π
ρ
π
ρϕρ
ϕ
2
0
4
2
0
0
21
0
r
ddr
. Интегрирование по
ϕ
дает
∫
=
−
0
0
4
2
0
21
2
ρ
ρρ
ϕ
r
dr
. Так как
22
0
2
ρ
+= rr
.
Окончательно получим
2
0
2
0
2
0
0
22
0
2
22
0
21
0
)( rr
dr
+
=
+
=
∫
−
ρ
ρ
ρ
ρ
ϕ
ρ
.
При 10
210
==
−
ϕ
r . Если .0,
210
=∞=
−
ϕ
тоr
2.Табличный метод.
Для многих поверхностей, широко используемых в инженерной практике, угловые
коэффициенты излучения представлены в графической форме (см. рис.27.5а).
3. Алгебра угловых коэффициентов.
Метод позволяет, используя табличные угловые коэффициенты, определить
угловые коэффициенты бóльшего класса геометрических форм. Предположим, что
необходимо определить ϕ
1
→
3
(см. рис.27.6), F
4
=F
2
+F
3
. Лучистую энергию, падающую
на поверхность F
4
от
поверхности F
1
, можно представить в
виде
311121114111 →→→
+=
ϕϕϕ
FEFEFE ,тогда ,,
214131312141 →→→→→→
−=+=
ϕϕϕϕϕϕ
где
ϕ
1
→
4
и ϕ
1
→
2
- табличные угловые коэффициенты.
4. Метод натянутых нитей.
При нахождения угловых коэффициентов для двух бесконечных в одном направлении
поверхностей используется формула
( ) ( )
[ ]
,
2
1
1
21
dbcadacb
l
+−+=
→
ϕ
(27.23)
d
ϕ
dF
2
d
ρ
ρ
F
1
r
0
r
F
2
ρ
0
θ
F
1
<<
F
2
Рис. 27.5
Рис.27.5а
Рис.27.6
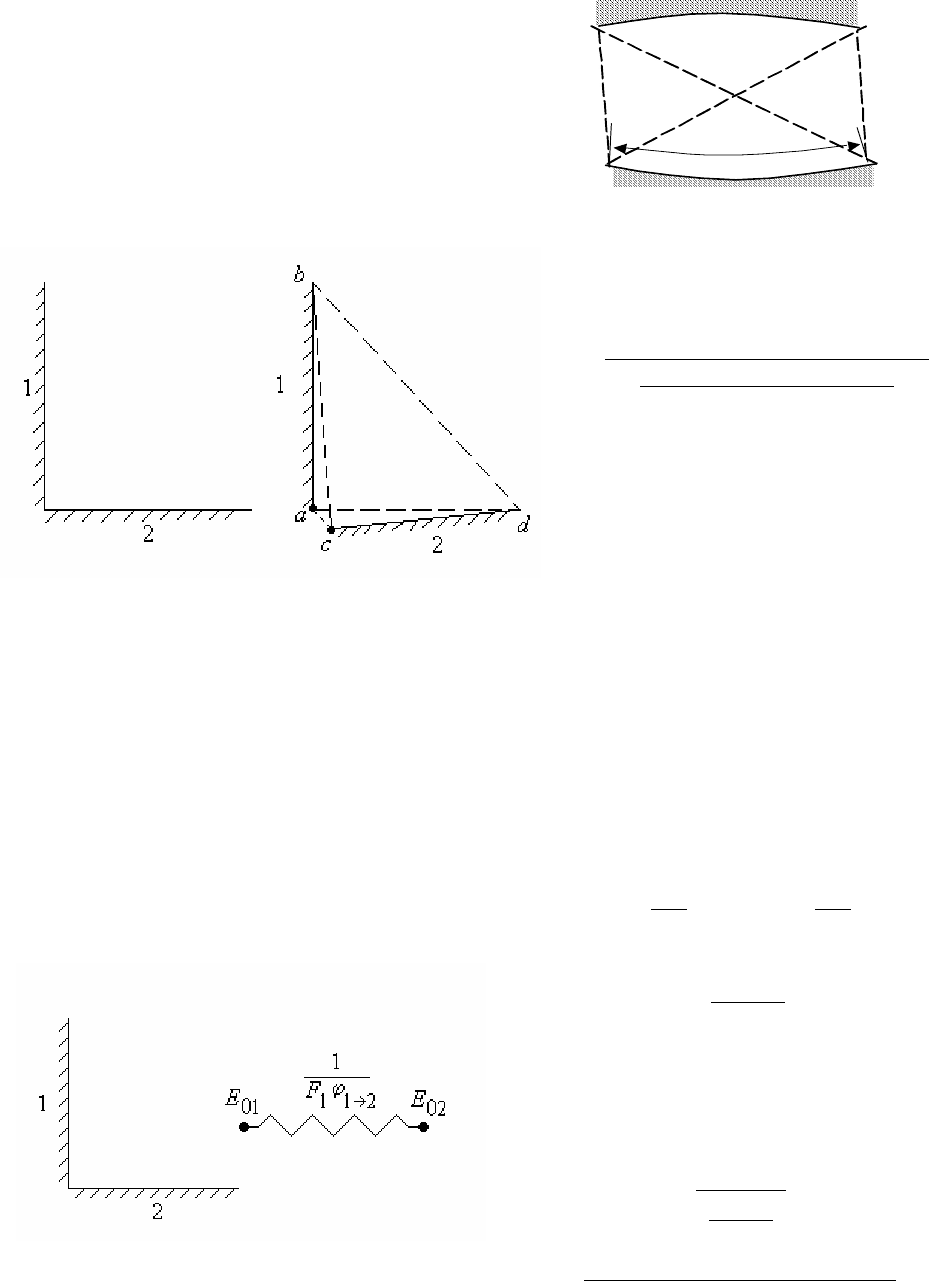
291
где (cb + da) - сумма длин пересекающихся
нитей (рис.27.7); (ca + db) -
непересекающихся нитей.
Если излучающие поверхности образуют
угол (см. рис.27.8), то две поверхности у
вершины угла раздвигают и проводят нити,
а затем в формуле (27.23) считают, что
aс = 0.
Кроме рассмотренных методов существуют
и другие - графоаналитический,
световой и электрический.
Теплообмен излучением между
черными поверхностями
Напомним, что черные
поверхности являются
диффузионными, а лучистая энергия,
падающая на них, полностью ими
поглощается. Поток энергии
излучения, испущенный первой
поверхностью, и поглощенный
второй, запишется в виде
,
2110121 →→
=
ϕ
FEE
поток лучистой энергии, поглощенный первой поверхностью -
.
1220212 →→
=
ϕ
FEE
Поток теплоты, который получит вторая поверхность от первой
.
122022110121 →→→
−=
ϕϕ
FEFEQ
&
Используя условие взаимности
,
212121
FF
→→
=
ϕϕ
можно написать
(
)
211020121 →→
−=
ϕ
FEEQ
&
Вт,
где
.
100
;
100
4
2
002
4
1
001
=
=
T
CE
T
CE
Вводя понятие геометрического
сопротивления
211
1
→
ϕ
ϕ
F
, которое
обусловлено тем, что не все излучение,
испущенное одной поверхностью,
достигнет другой, получим
.
1
211
0201
21
→
→
−
=
ϕ
F
EE
Q
&
(27.24)
Адиабатическая поверхность
Если в системе тел, обменивающихся
лучистой энергией, к одной из поверхностей теплота не подводится и не
отводится, то такая поверхность называется адиабатической (Q
рез
= 0). Температура
такой поверхности зависит от лучистой энергии окружающих ее тел и называется
2
1
a
b
c
d
l
1
Рис.27.7
Рис.27.8
Рис. 27.9
