Барилович В.А., Смирнов Ю.А. Основы технической термодинамики и теории тепло - и массообмена
Подождите немного. Документ загружается.

292
“плавающей “. Для системы, состоящей из двух черных тел и адиабатической
поверхности (см. рис.27.10), можно написать
,
11
322
0203
311
0301
→→
−
=
−
ϕϕ
F
EE
F
EE
откуда можно найти . затем а,
100
3
4
3
003
Т
T
CE
=
Теплообмен излучением между серыми телами.
Лучистая энергия, излучаемая серым телом,
называется эффективной лучистой энергией. Она
складывается из собственной Е
соб
и отраженной
Е
отр
:
,
пад
11
соб
1
отрсоб
1
эф
1
EREEEE +=+=
откуда .
1
1
соб
1
эф
пад
R
EE
E
−
= (а)
Для того чтобы тела, обменивающиеся лучистой
энергией, имели неизменную температуру, к ним
необходимо подводить (отводить) результирующую
теплоту
(
)
.
1
падэф
11
рез
FEEQ −=
&
(b)
Подставим (а) в (b)
,
1
1
соб
1
эф
1
эф
11
1
1
соб
1
эф
1
эф
1
рез
1
F
R
EEER
F
R
EE
EQ
+−
=
−
−=
&
но для серой поверхности
1
11
=+ R
ε
, тогда
1
1
011
эф
111
эф
1
эф
11
1
рез
F
R
EEREER
Q
+−−
=
εε
&
,
или ,
11
1
эф
101
1
рез
ε
F
R
EE
Q
−
=
&
(27.25)
где
11
1
ε
F
R
– поверхностное сопротивление серого тела.
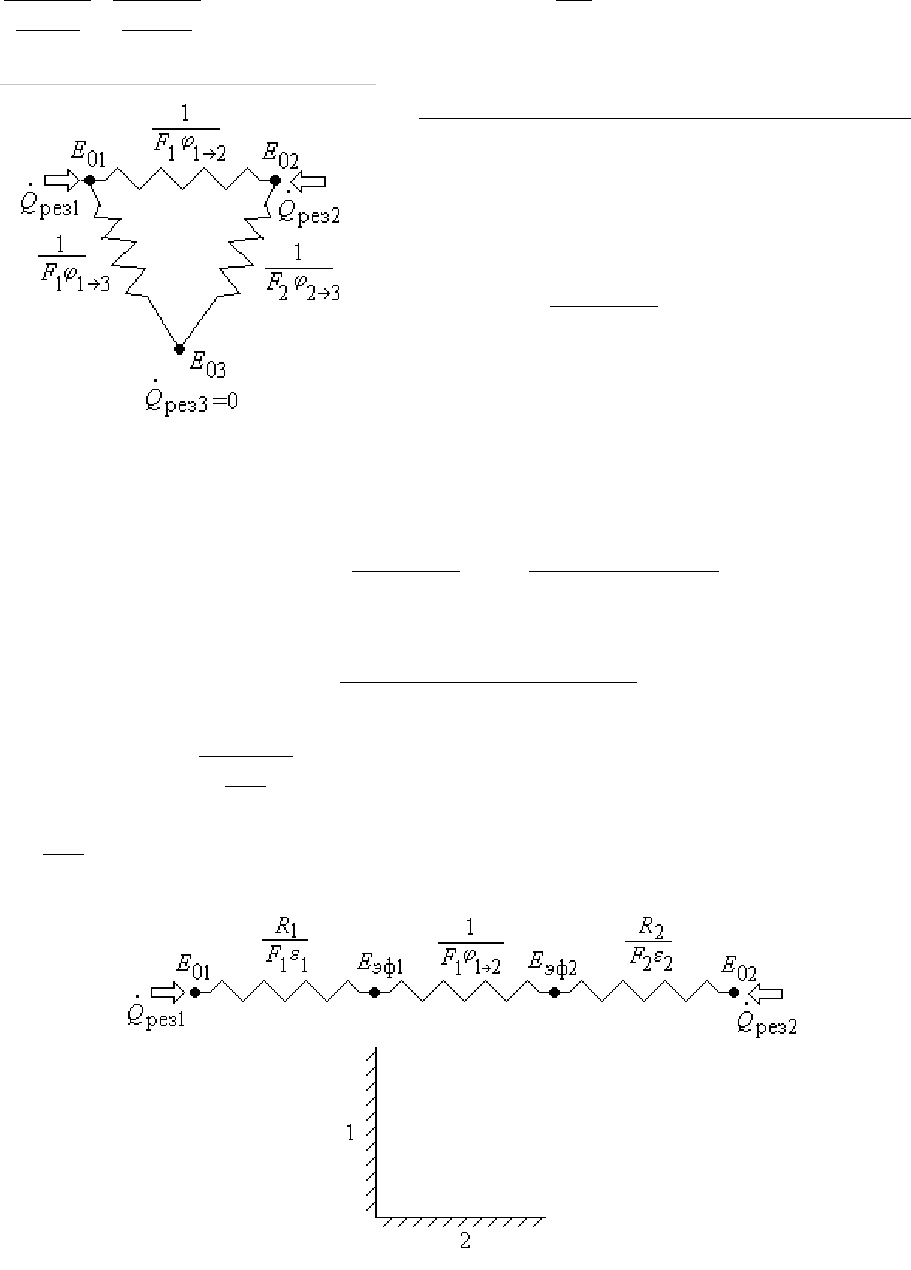
Рис.27.11
Рис.27.10
293
Тогда для двух серых тел, обменивающихся лучистой энергией, тепловой поток,
переданный от первой поверхности ко второй будет иметь вид:
22
2
21111
1
0201
21
1
F
R
FF
R
EE
Q
εϕε
++
−
=
→
→
&
. (27.26)
Рассмотрим три частных случая.
1.Две бесконечные параллельные пластины. Для них можно написать
(
)
,
1
1
1
2
2
1
1
0201
21
ε
ε
ε
ε
−
++
−
−
=
→
FEE
Q
&
(
)
.
1
11
21
0201
21
−+
−
=
→
εε
FEE
Q
&
Введем понятие приведенной степени черноты
;
1
11
1
21
пр
−+
=
εε
ε
но,
100100
4
2
0
4
1
0пр21
−
=
→
T
C
T
CFQ
ε
&
С
пр
= С
0
ε
пр
, тогда
−
=
→
4
2
4
1
пр21
100100
TT
FCQ
&
. (27.27)
2.Два бесконечных цилиндра (первый охватывает второй),
ϕ
1
→
2
=1.
Используя (27.26), получим
.
1
11
)(
2
1
21
10201
21
F
F
FEE
Q
−+
−
=
→
εε
&
3.Небольшое серое тело с поверхностью F
1
охватывается оболочкой, у которой F
2
>> F
1
.
(
)
(
)
1
1
1
1
1
1
1
1
02
01
1
1
1
02
01
2
2
2
2
1
1
1
1
1
02
01
2
1
− +
−
=
+
−
−
=
+ +
−
=
→
→
ε
ε
ε
ε ϕ ε
F
E
E
F
E
E
F
R
F
F
R
E
E
Q
&
,,
0
1
1011
C
C
СС ==
εε
.
100100
1
4
2
4
1
121
F
TT
CQ
−
=
→
&
(27.28)
Из формулы (27.28) видно,
что в этом случае поток
теплоты зависит
только от
коэффициента излучения
первого серого тела.
Если лучистый
теплообмен осуществляется
между тремя
поверхностями, то
эквивалентная электрическая
схема будет иметь вид,
показанный на рис.27.12.
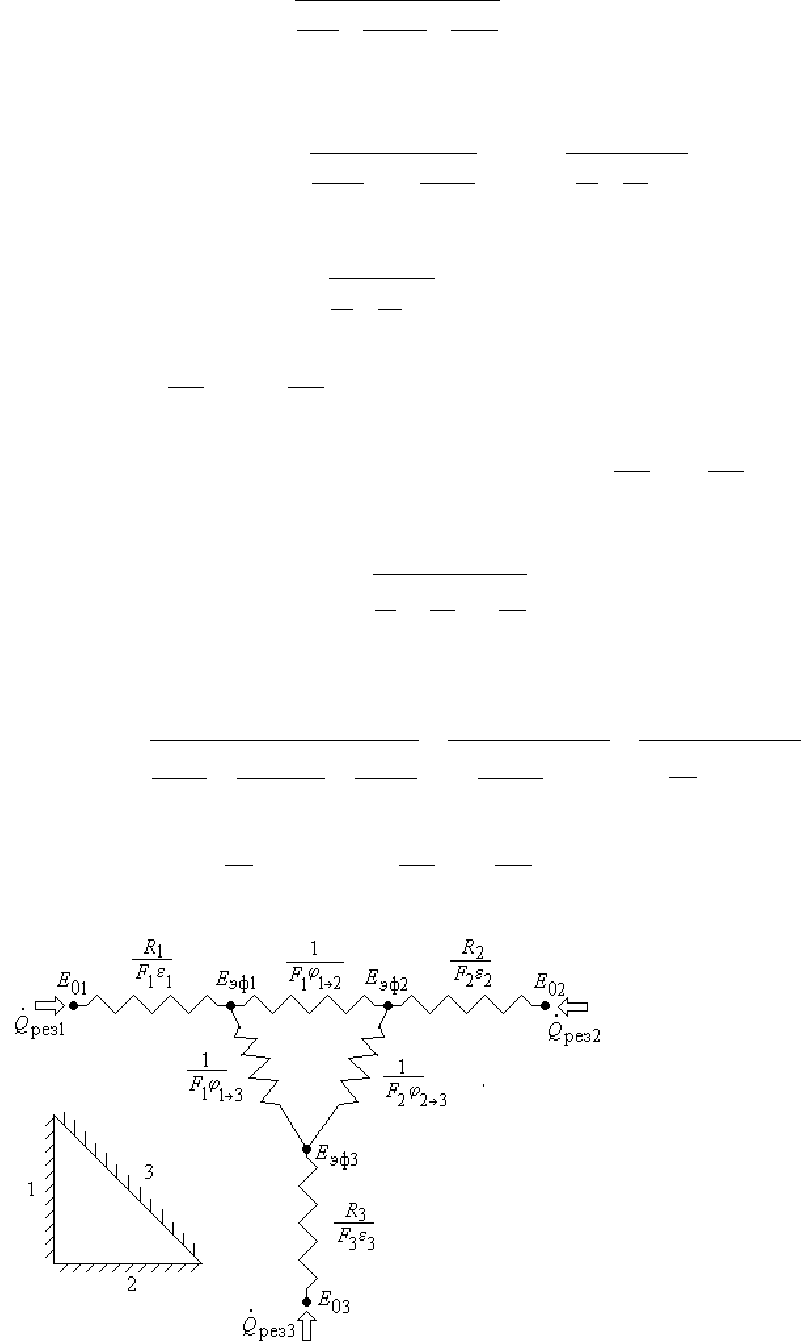
Рис.27.12

294
Перенос излучения в поглощающих - пропускающих средах
До сих пор считалось, что между телами, обменивающимися лучистой энергией,
среда была прозрачной. Однако стекло, газы с несимметричной структурой
молекулы ( H
2
O, CO
2,
SO
2,
NH
3
) могут как излучать, так и поглощать лучистую
энергию. Лучистая энергия, проходя через полупрозрачную среду, поглощается ею.
Будем считать, что собственное излучение среды мало, тогда на длине dx
ослабление, например, спектральной интенсивности dI
λ
найдем из выражения
,dxIdI
x
λλλ
α
−
=
где I
λ
x
- интенсивность излучения на координате x;
α
λ
- спектральный коэффициент
поглощения среды.
Разделив переменные и считая α
λ
= const, после интегрирования получим закон
Бугера
x
xx
eII
λ
α
λλ
−
=
=
0,
. (27.29)
Лучистая энергия, поглощаемая слоем
)1(
0,0,
x
xxx
eIIII
λ
α
λλλ
−
==
−=−=∆
,
тогда спектральные коэффициент поглощения и степень черноты найдем из
выражения
.1
0,
0,
x
x
xx
e
I
II
A
λ
α
λ
λλ
λλ
ε
−
=
=
−=
−
==
Как было показано ранее, для серых тел A
λ
= A ,
ε
λ
=
ε
, A =
ε
.
Рассмотрим лучистый теплообмен между двумя серыми бесконечными
параллельными пластинами (ϕ
1-2
= 1), между которыми находится непрозрачный газ.
Лучистую энергию, падающую на первое тело, можно записать в виде:
0
гггэф
2
ггэф
2
пад
1
EDEEDEE
ε
+=+= .
Найдем поток теплоты, который необходимо подвести к первому телу, чтобы его
температура осталась неизменной
(
)
1
пад
1
эф
11
рез
FEEQ −=
&
.
С учетом предыдущего уравнения можно написать
(
)
10
гггэф
2
эф
11
рез
FEDEEQ
ε
−−=
&
.
Воспользуемся балансным уравнением:
ггг
++1 RDА=
, но для нашего случая А
г
=
ε
г
, R
г
= 0, тогда
гг
+1 D
ε
=
. С учетом
этого выражения
гэф
1
гэф
1
эф
1
эф
1
1 DEEEE +=⋅=
ε
, поэтому
(
)
10
гггэф
2
гэф
1
гэф
11
рез
FEDEDEEQ
εε
−−+=
&
или
г
1
г
01
эф
г
121
2
эф
1
эф
1
рез
1
Е
1
εϕ
F
Е
DF
ЕE
Q
−
+
−
=
&
, (a)
где учитывается, что в общем случае ϕ
1-2
≠ 1. Последняя запись уравнения позволяет
передачу лучистой энергии между телами изобразить в виде эквивалентной
электрической схемы (рис.27.13):

295
Рис.27.13
Аналогичные уравнения можно написать для второй пластины.
22
пад
2
эф
2
резг
0
гг
1
эф
2
пад
)(, FЕЕQЕDЕЕ −=+=
&
ε
,
2
г
г
02
эф
122
г
1
эф
2
эф
2
рез
11
F
ЕЕ
FD
ЕЕ
Q
εϕ
−
+
−
=
−
&
(b
)
Так как 0
рез
=Σ
i
Q
&
, то
2
рез
1
рез
QQ
&&
−= . Отсюда можно определить
4
г
00г
100
=
Т
СЕ
, а
затем Т
г
. Таким образом, потенциал Е
0
г
,
как и потенциал адиабатической стенки,
является плавающим и зависит от температуры других поверхностей.
Определим тепловой поток, который получит второе тело от первого:
22
2
экв
11
1
0201
12
F
R
R
F
R
EE
Q
εε
++
−
=
&
, (27.30)
где
г2г1г121
г2г1г121
экв
111
111
=
εεϕ
εεϕ
FFDF
FFDF
R
++
+
-
эквивалентное
сопротивление
,
полученное
из
параллельного
соединения
сопротивлений
R
1
=
г211
1
DF
−
ϕ
и
R
2
=
г2г1
11
εε
FF
+ (
напомним
,
что
при
параллельном
соединении
сопротивлений
складываются
их
проводимости
,
то
есть
21экв
111
RRR
+= ).
Действие
защитных
экранов
Чтобы
уменьшить
поток
лучистой
энергии
от
одного
тела
к
другому
,
между
ними
устанавливают
защитные
экраны
.
При
отсутствии
экрана
для
двух
бесконечных
параллельных
серых
пластин
можно
написать
−
4
2
4
1
пр2-1
100100
=
TT
Cq
Вт
/
м
2
,

296
где
021
пр
111
1
CCC
C
−+
= ; C
1
=
ε
1
C
0
; C
2
=
ε
2
C
0
.
Будем
считать
,
что
СССС
===
э21
.
Поместим
между
телами
экран
,
который
представляет
собой
тонкую
пластину
,
и
составим
уравнения
теплового
баланса
.
Так
как
экран
тонкий
,
то
его
температура
одинакова
с
обеих
сторон
,
следовательно
−
4
э
4
1
прэ-1
100100
=
T
T
Cq , (
а
)
−
4
2
4
э
пр2-э
100100
=
T
T
Cq , (
б
)
но
q
1-
э
= q
э
-2
.
Приравнивая
(
а
)
и
(
б
),
найдем
+
=
4
2
4
1
4
э
1001002
1
100
ТТТ
.
Подставим
это
выражение
в
(
а
),
тогда
:
−
=
4
2
4
1
прэ2)-1(
1001002
1
ТТ
Cq , (27.31)
т
.
е
.
при
установке
экрана
плотность
теплового
потока
уменьшается
в
два
раза
:
1)=(,
2
q
2-1
э2)-(1
n
q
= .
Если
имеется
n
экранов
,
то
1
+
2-1
э
n
q
q = .
Рассмотрим
второй
случай
,
когда
.
а
, ==
э21
CCCCC ≠
−
4
2
4
1
пр2-1
100100
=
TT
Cq ,
−
4
э
4
1
прэ1э-1
100100
=
T
T
Cq , (
а
)
где
0э1
прэ1
111
1
ССС
C
−+
= .
−
4
2
4
э
прэ22-э
100100
=
T
T
Cq , (
б
)
где
02э
2прэ
111
1
ССС
C
−+
= ,
но
в
нашем
случае
С
1 =
С
2
=
С
,
следовательно
,
С
прэ
1 =
С
прэ
2
=
С
прэ
.
Приравнивая
(
а
)
и
(
б
)
с
учетом
сказанного
,
получим
+
=
4
2
4
1
4
100
Т
100
Т
2
1
100
Т
э
. (
с
)
Подставим
(
с
)
в
(
а
) :
пр
прэ2-1
4
2
4
1
прэ
э-1
21001002
=
C
С
q
TT
С
q =
−
, (27.32)

297
то
есть
( )
пр
прэ
2-1
э2-1
2
С
C
q
q
= .
Если
в
качестве
экрана
используется
,
например
,
медь
,
покрытая
окисью
,
у
которой
С
э
= 3,18 ,
а
у
стенки
С
= 5,38,
то
( )
0,144
2-1
э2-1
≈
q
q
,
т
.
е
.
тепловой
поток
между
поверхностями
при
установке
экрана
уменьшается
в
6,94
раза
.
Измерение
высоких
температур
Измерение
температуры
поверхности
высоконагретого
тела
контактным
способом
при
помощи
термометров
и
термопар
встречает
значительные
технические
трудности
.
В
связи
с
этим
широко
используются
оптические
методы
,
которые
позволяют
измерять
температуру
поверхности
тела
с
достаточной
точностью
не
касаясь
самого
тела
.
При
этом
вводятся
такие
понятия
как
радиационная
,
цветная
и
яркостная
температуры
.
Определив
эти
температуры
из
опыта
,
находят
действительные
значения
температур
.
Так
,
из
равенства
лучистых
энергий
можно
установить
связь
между
радиационной
и
истинной
температурами
)()(
.0
TETE
рад
= ,
но
4
0
4
.0
TT
рад
εσσ
= ,
тогда
4
1
.
ε
рад
T
T =
.
Из
соотношения
)(
)(
)(
)(
2
1
20
1
0
TE
TE
TE
TE
Ц
Ц
λ
λ
λ
λ
=
с
учетом
закона
Вина
найдем
зависимость
между
T
Ц
и
T.
Действительно
,
подстановка
дает
1
)
11
(
2
)
11
(
12
2
12
2
λ
λλ
λ
λλ
εε
−
−
=
T
C
T
C
ee
Ц
.
После
логарифмирования
получим
:
−
=−
21
2
2
1
11
ln
11
λλ
ε
ε
λ
λ
C
TT
Ц
.
Подставив
закон
Вина
в
равенство
)()()(
00
TETETE
Я
λλλλ
ε
== ,
найдем
связь
между
яркостной
и
действительной
температурами
.
lg
11
2
CTT
Я
λ
ε
λ
=−
Сложный
теплообмен
В
реальных
системах
,
как
правило
,
имеет
место
сложный
теплообмен
,
то
есть
суммарный
тепловой
поток
складывается
из
потоков
,
обусловленных
теплопроводностью
,
конвекцией
и
лучистым
теплообменом
.
В
связи
с
этим
при
расчетах
необходимо
определить
долю
каждого
из
них
,
и
если
у
какого
-
то
потока
она
мала
,
то
в
дальнейшем
исключить
его
из
рассмотрения
.
При
передаче
теплоты
,
например
,
от
одной
пластины
к
другой
,
когда
отсутствуют
конвективные
токи
(
зазор
δ
мал
),
плотность
теплового
потока
можно
записать
в
виде
:
( )
−
=
4
2
4
1
пр
21
г
100100
+-
TT
C
ТТ
q
δ
λ
. (27.33)
Уравнение
теплового
баланса
для
элемента
ребра
представим
так
:

298
( )
dx
Т
Т
СdxTTdx
dx
Td
f Π
−
Π
4
ос
4
р
оср
2
р
2
рр
100100
+-=
αλ
,
где
П
-
периметр
ребра
; f
р
-
площадь
поперечного
сечения
ребра
;
р0р
;
εε
СС
= -
степень
черноты
поверхности
ребра
.
Радиационные
свойства
газов
В
отличие
от
серых
тел
,
газы
обладают
ярко
выраженными
спектральными
свойствами
,
т
.
е
.
при
определенной
длине
волны
они
могут
хорошо
поглощать
лучистую
энергию
,
а
при
другой
-
быть
прозрачными
.
Если
лучистая
энергия
,
испускаемая
серыми
телами
,
определяется
свойствами
поверхности
,
то
поглощательная
и
излучательная
способности
газов
зависят
от
их
объема
.
Поэтому
для
произвольных
объемах
вводят
понятие
средней
длины
пути
луча
:
F
V
L 3,6= ,
где
F -
поверхность
газового
объема
.
Так
,
для
сферы
DL
3
2
= ,
для
бесконечных
параллельных
стенок
δ
2=L ,
для
бесконечного
цилиндра
L= D.
Интегральная
степень
черноты
газов
зависит
от
температуры
и
от
произведения
средней
длины
пути
луча
и
парциального
давления
газа
(
рис
.27.14),
то
есть
ε
г
= f (T
г
, L
⋅
p
г
).
Если
газ
находится
при
давлении
выше
атмосферного
,
то
вводят
поправку
.
Так
,
для
водяного
пара
можно
написать
О
2
НО
2
НО
2
Н
С
⋅=
′
εε
,
где
ОН
2
С
-
коэффициент
,
зависящий
от
давления
(
см
.
рис
.27.15).
Степень
черноты
для
смеси
газов
определяется
по
формуле
εεεε
∆−+=
22
СООНсм
.
Величина
∆
ε
характеризует
переизлучение
газов
,
когда
длины
излучаемых
волн
перекрывают
друг
друга
.
Коэффициент
поглощения
водяного
пара
находят
из
выражения
:
О
2
Н
О
2
Н
О
2
Н
45,0
w
*
О
2
Н
C
Т
Т
А
=
ε
,
где ,,
w
w
*
О
2
Н
О
2
Н
О
2
Н
= Т
T
T
Lрf
ε
w
Т
-
температура
излучателя
.
В
этом
случае
при
определении
*
2
ОН
ε
используется
график
(
)
г
,
О
2
Н
О
2
Н
TL
р
f
=
ε
(
см
.
рис
.27.14),
но
вместо
г
Т
подставляют
температуру
излучателя
w
Т
,
а
L
р
ОН
2
умножают
на
О
2
Н
w
T
T
.
Для
СО
2
справедлива
формула
:
2
2
2
СО
2
СО
65,0
w
СО
*
СО
C
Т
Т
А
=
ε
.
Поглощательная
способность
смеси
определяется
выражением
АААА ∆−
22
СООНсм
+= ,
где
ε
∆
∆
=А (
при
температуре
w
Т
).
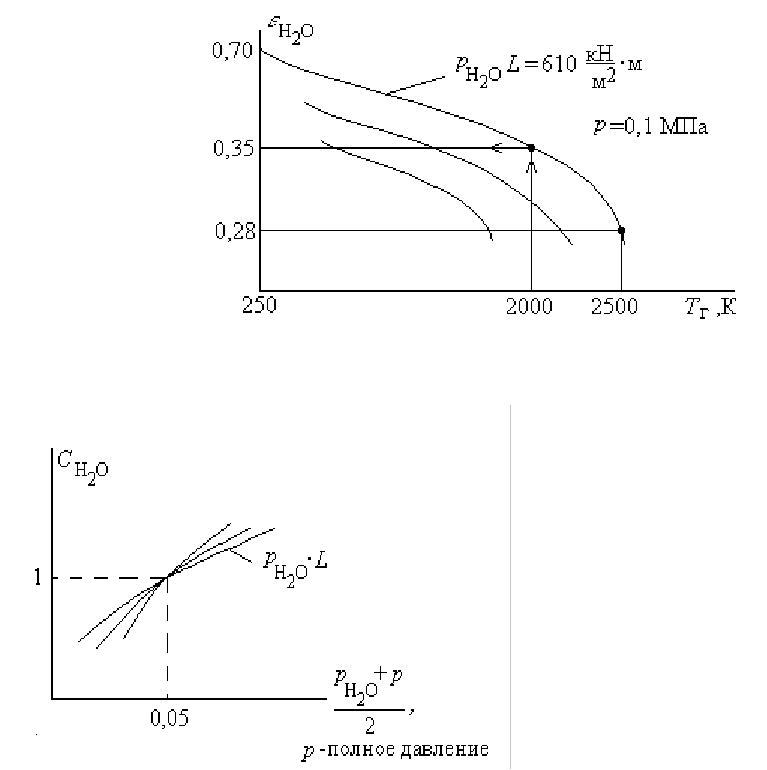
299
Рис
.27.14
28. Теплообменные аппараты
Теплообменные
аппараты
(
ТА
)
предназначены
для
нагревания
одного
из
теплоносителей
(
агента
)
за
счет
охлаждения
другого
.
Теплообменные
аппараты
делятся
на
четыре
основных
типа
.
1.
Рекуперативные
ТА
,
в
которых
теплота
от
одного
агента
к
другому
передается
через
твердую
стенку
.
2.
Регенеративные
ТА
,
где
процесс
передачи
теплоты
осуществляется
в
нестационарных
условиях
:
сначала
горячий
теплоноситель
нагревает
насадку
,
аккумулирующую
теплоту
,
затем
через
эту
насадку
пропускают
нагреваемый
поток
.
Такие
аппараты
находят
применение
,
например
,
в
транспортных
газотурбинных
установках
.
3.
ТА
смесительного
типа
,
в
которых
агенты
перемешиваются
.
По
этому
принципу
работают
водоподогреватели
паросиловых
установок
,
инжекторы
.
4.
ТА
с
внутренними
источниками
теплоты
(
например
,
реакторы
АЭС
).
По
характеру
взаимного
движения
теплоносителя
рекуперативные
ТА
разделяются
на
прямоточные
и
противоточные
(
рис
.28.1).
Рис
.27.15

300
Рис
. 28.1
Уравнение
теплового
баланса
и
теплопередачи
Рассмотрим
прямоточный
теплообменник
.
Будем
полагать
,
что
в
ТА
происходит
передача
теплоты
без
потерь
в
окружающую
среду
от
горячего
агента
1
с
расходом
1
G
&
к
холодному
агенту
2
с
расходом
2
G
&
.
Тогда
элементарный
тепловой
поток
,
отдаваемый
первым
агентом
и
получаемый
вторым
,
будет
равен
соответственно
убыли
или
увеличению
энтальпии
агентов
при
изменении
их
температур
на
21
и
dtdt
:
11111
dtGcIdQd
p
&
&
&
−=−= , (
а
)
22222
dtGcIdQd
p
&
&
&
== . (b)
Введем
понятие
массовой
(
расходной
)
теплоемкости
GcW
p
&
=
и
приравняем
элементарные
тепловые
потоки
,
определяемые
(
а
)
и
(b):
1122
dtWdtW −=
,
или
1
2
2
1
W
W
dt
dt
−= .
Из
соотношения
видно
,
что
чем
больше
расходная
теплоемкость
,
тем
меньше
изменение
температуры
соответствующего
агента
.
Интегрируя
(
а
)
и
(b),
получим
(
)
11111
ttGcQ
p
′
−
′′
−=
&&
,
(
)
11111
ttGcQ
p
′′
−
′
=
&&
, (c)
(
)
22222
ttGcQ
p
′
−
′′
=
&&
. (d)
Запишем
уравнение
теплопередачи
в
дифференциальной
форме
tdFkQd ∆=
&
, (e)
где
∆t -
текущий
температурный
напор
между
агентами
; k –
локальный
коэффициент
теплопередачи
; dF -
элементарная
площадка
теплопередающей
поверхности
.
В
интегральной
форме
будем
иметь
FtkQ
__
∆=
&
. (f)
Уравнение
теплопередачи
(f)
используется
чаще
всего
для
определения
требуемой
поверхности
теплообмена
.
Определим
температурный
напор
между
потоками
.
Так
как
22
2
11
1
,
Gc
Qd
dt
Gc
Qd
dt
pp
&
&
&
&
=−=
,
то
можно
написать
( )
Qd
WW
tddtdt
&
+−=∆=−
21
21
11
,
или
обозначая
+=
21
11
WW
m
,

301
(
)
Qdmtd
&
−=∆ .
После
подстановки
выражения
для
Qd
&
из
(e) ,
получаем
( )
(
)
., mkdF
t
td
tdFmktd −=
∆
∆
∆−=∆
Интегрирование
последнего
уравнения
от
t
′
∆
до
∆t
х
и
от
0
до
F
х
дает
:
x
x
mkF
t
t
−=
′
∆
∆
ln ,
откуда
(
)
xx
mkFtt −
′
∆=∆ exp , (28.1)
где
t
′
∆
-
температурный
напор
между
теплоносителями
на
входе
в
ТА
.
Уравнение
(28.1)
представляет
изменение
локального
температурного
напора
вдоль
поверхности
теплообмена
F
при
прямотоке
.
Определим
выражение
для
среднего
по
поверхности
температурного
напора
( )
(
)
)2.28(,
ln
ln
1
ln
1
ln
1
__
м
б
мб
mkF
F
mkF
F
mkF
F
x
t
t
tt
t
t
tt
t
t
t
t
t
e
t
t
t
mkFde
mkF
t
dFe
F
t
dFt
F
t
∆
∆
∆−∆
=
′
∆
′′
∆
′′
∆−
′
∆
=
−
′
∆
′′
∆
′
∆
′′
∆
′
∆
=
=−
′
∆
′′
∆
′
∆
=
′
∆
=
′
∆
=∆=∆
−−−
∫∫∫
где
б
t∆
и
м
t∆ -
соответственно
наибольший
и
наименьший
температурные
напоры
.
Формула
(28.2)
представляет
среднелогарифмический
температурный
напор
между
агентами
и
может
использоваться
при
расчете
рекуперативных
ТА
как
с
прямоточным
,
так
и
с
противоточным
движением
теплоносителей
.
Так
как
в
реальных
теплообменных
аппаратах
движение
потоков
является
более
сложным
,
чем
в
теплообменнике
“
труба
в
трубе
”,
то
действительный
температурный
напор
определяют
по
формуле
td
tt
∆
⋅∆=∆
ε
,
где
t∆
ε
учитывает
как
направление
движения
потоков
,
так
и
число
ходов
∆
=
∆
====
∆
'
max
2
'
2
1
;;),(
δ
δ
δ
δ
δ
δ
ε
t
t
P
t
t
RPRf
t
(
см
.
рис
.28.2
и
рис
.28.3).
Если
число
ходов
в
ТА
больше
трех
,
то
.1=
∆t
ε
Рис
. 28.2
Рис
.28.3
