Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

A.1 Approximation 565

(x) = 0 ; x < x

i−1

and x > x

i+1

x −x

i−1

∆

; x

i−1

< x < x

(A.16)

i+1

−x

∆

; x

< x < x

i+1

For the terminal nodes, i = (1, N +1), these functions take the form illustrated in

Figure A.3 (b).

In particular, we have

) = 1 ; i = j

= 0 ; i 6= j (A.17)

and hence

∗

= C

, (A.18)

from equations (A.1, A.14, A.17). In other words, the coefﬁcients C

are also the

nodal values f

∗

The piecewise linear shape functions (A.16) are zero everywhere except in the

two elements adjacent to node i and hence most of the components K

of the coefﬁ-

cient matrix (A.12) will be zero. Non-zero values are obtained only when |j−i|= 0

or 1 and in these cases the only contributions to the integral (A.12) come from at

most two elements. Substituting (A.16) into (A.12) and performing the resulting el-

ementary integrations, we ﬁnd

∆

; i = j

∆

; |i − j| = 1 (A.19)

= 0 ; |i − j| > 1 ,

except for the end nodes, i = 1 and i = N +1, where the functions on Figure A.3 (b)

must be used and we have

∆

; i = j = 1 or N + 1

∆

; |i − j| = 1 (A.20)

= 0 ; |i − j|> 1 .

For example, if there are 7 elements and 8 nodes, the matrix K will be

K =

∆







2 1 0 0 0 0 0 0

1 4 1 0 0 0 0 0

0 1 4 1 0 0 0 0

0 0 1 4 1 0 0 0

0 0 0 1 4 1 0 0

0 0 0 0 1 4 1 0

0 0 0 0 0 1 4 1

0 0 0 0 0 0 1 2







. (A.21)

566 A The Finite Element Method

Notice that the matrix is symmetric [as is clear from equation (A.12)] and it is also

banded — i.e. non-zero values occur only on or near the diagonal. The reader will

recall from §3.9 that the stiffness matrix for an elastic system is also symmetric

and banded. Indeed, when the ﬁnite element method is applied to problems in linear

elasticity, the resulting matrix K will be identical to the stiffness matrix of the system

of elements, each regarded as elementary elastic components (generalized springs).

For this reason, the matrix K is generally known as the stiffness matrix and this

terminology is often retained even in cases where the ﬁnite element method is applied

to other physical processes, such as the conduction of heat.

Example A.1

Find a piecewise linear approximation to the exponential function e

in the range

0 < x < 1, using two equal elements and three nodes, 0,0.5,1. Plot a graph com-

paring the function and its approximation. Plot also the piecewise linear function

obtained using the collocation method with the same three points and comment on

the comparison.

In this case, we have

∆

=0.5 and the coefﬁcient matrix is

K =





2 1 0

1 4 1

0 1 2





For F

, we have

(x)dx =

0.5

(1 −2x)dx =



−2xe



0.5

= 2e

0.5

−3

= 0.2974

Similar calculations for F

yield

= 2e −4e

0.5

+ 2 = 0.8417

= 2e

0.5

−e = 0.5792

Substituting into (A.11) and solving the resulting equations, we obtain

= f

∗

= f

∗

(0) = 0.9779

= f

∗

= f

∗

(0.5) = 1.6135

= f

∗

= f

∗

(1) = 2.6682 .

The resulting piecewise linear approximation is compared with the exponential

function in Figure A.4. If the collocation method is used instead, we obtain the dotted

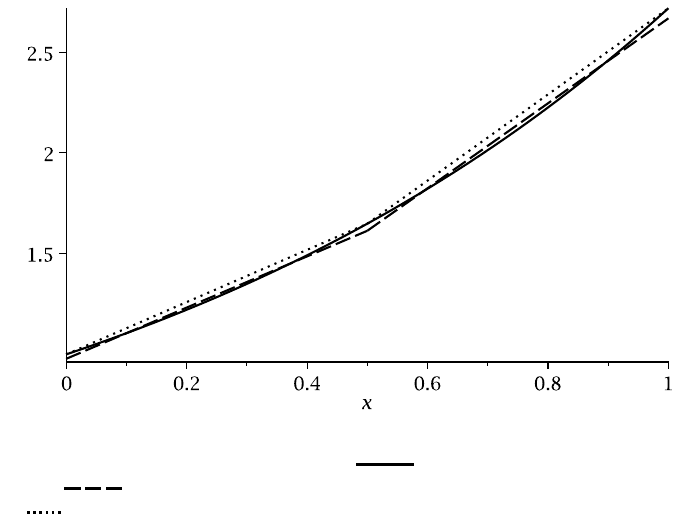
A.2 Axial loading 567

curve in this Figure. It is clear that the collocation approximation is less accurate in

this case, since it always lies on one side of the exact curve, except at the collocation

points.

Figure A.4: The exact exponential curve ( ), the piecewise linear approxima-

tion (

), and a piecewise linear approximation using the collocation method

(

A.2 Axial loading

The simplest application of the ﬁnite element method in mechanics of materials con-

cerns the determination of the displacement of a bar subjected to axial loading. We

shall use this example to illustrate the arguments underlying the method and also

to explore the relation between the structural mechanics and Rayleigh-Ritz formula-

tions.

A.2.1 The structural mechanics approach

Figure A.5 shows an elastic bar of length L, supported at x = 0 and loaded by a

distributed load p(x) per unit length and an end load F

at x =L. In the most general

case, the cross-sectional area A and Young’s modulus E can vary along the bar and

hence be functions of x, but for the moment we shall restrict attention to the simpler

case where E,A are independent of x.

568 A The Finite Element Method

p(x)

cross-sectional

area A(x)

Figure A.5: Axial loading of the bar

To obtain an approximate solution of the problem, we consider the bar to be made

up of a set of N equal elements, each of length

∆

as shown in Figure A.6 (a). The elements are numbered i = (1,N), starting from the

left end. As in §A.1.3, the deformation of the bar will be characterized by the set of

nodal displacements u

, which are the displacements of the points x

=iL/N.

i-1

∆

(a) (b)

Figure A.6: (a) Subdivision of the bar into N equal elements, (b) Nodal forces and

displacements for the i-th element

The ﬁrst stage in the analysis is to determine the relation between the nodal forces

on an individual element and the displacements of its ends. The i-th element is shown

in Figure A.6 (b). The displacements of its ends are u

i−1

, and the corresponding

nodal forces are F

i−1

, respectively. The element is a uniform bar of length

∆

cross-sectional area A and Young’s modulus E, so it behaves as a linear spring of

stiffness

k =

∆

The extension of the element is

= u

−u

i−1

and hence the element nodal forces and displacements are related by the equation

A.2 Axial loading 569

= −F

i−1

∆

−u

i−1

) .

This equation can be written in the matrix form

∆



1 −1

−1 1



i−1





i−1



, (A.22)

where the matrix

∆



1 −1

−1 1



(A.23)

is known as the element stiffness matrix.

A.2.2 Assembly of the global stiffness matrix

The next stage is to use the properties of the individual elements to assemble the

stiffness matrix K, for the whole structure, deﬁned such that

F = Ku ,

where F is the vector of nodal forces for the structure. The matrix K is known as

the global stiffness matrix.

Consider the special case in which the components of the nodal displacement

vector u are given by u

. In other words, the k-th node is given a unit dis-

placement (u

= 1) and the other nodal displacements are zero (u

= 0,i 6= k). The

corresponding nodal forces are then given by

∑

i=1

= K

and hence the k-th column of the global stiffness matrix K is equal to the nodal force

vector F required to produce the displacement ﬁeld u

. This in turn is the sum

of the force vectors needed to deform the elements adjacent to node k and is obtained

by summing the corresponding components of the element stiffness matrices (A.23)

at their appropriate points in the global matrix.

Proceeding element by element, we obtain

∆







1 0 0 0 ... ...

0 0 0 0 ... ...

... ... ... ... ... ...







∆







1 −1 0 0 ... ...

−1 1 0 0 ... ...

0 0 0 0 ... ...

... ... ... ... ... ...







∆







0 0 0 0 ... ...

0 1 −1 0 ... ...

0 −1 1 0 ... ...

0 0 0 0 ... ...

... ... ... ... ... ...







∆







0 0 0 0 ... ...

0 0 1 −1 ... ...

0 0 −1 1 ... ...

... ... ... ... ... ...







+ ... , (A.24)

570 A The Finite Element Method

leading, for example, to

K =

∆







2 −1 0 0 0 0 0

−1 2 −1 0 0 0 0

0 −1 2 −1 0 0 0

0 0 −1 2 −1 0 0

0 0 0 −1 2 −1 0

0 0 0 0 −1 2 −1

0 0 0 0 0 −1 1







, (A.25)

for the case where N = 7. Notice how the resulting matrix is banded and is very

similar in form to that of equation (A.21).

An alternative way of obtaining (A.25) is to ﬁnd the force vector corresponding

to u

directly. Clearly only the two adjacent elements, k,k−1 will be deformed

and by superposition, using equation (A.22), we conclude that the required non-zero

forces are

k−1

= −

∆

; F

2EA

∆

; F

k+1

= −

∆

agreeing with the k-th column of (A.25).

A.2.3 The nodal forces

In order to complete the solution of the problem of Figure A.5, we need to determine

the nodal forces corresponding to the distributed loading p(x). In the simple case

where the load is uniformly distributed [p(x)= p

], it is reasonable to ‘share out’ the

load p

∆

acting on the i-th element equally between the two adjacent nodes x

i−1

This leads to the set of nodal forces

= p

∆

; i 6= N (A.26)

∆

+ F

. (A.27)

Notice that the end node (i=N) receives a contribution only from the element on its

left, but also experiences the end load F

We now have enough information to set up the equation system

Ku = F (A.28)

for the nodal displacements u

Example A.2

A uniform bar of cross-sectional area A and length L is loaded by a uniform force

per unit length. The end x= 0 is ﬁxed and the end x=L is unloaded. Estimate the

displacement at the free end using the ﬁnite element method with four equal length

elements. The material has Young’s modulus E.

A.2 Axial loading 571

For this problem,

∆

= L/4 and the stiffness matrix is obtained by analogy with

(A.25) as

K =

4EA







2 −1 0 0

−1 2 −1 0

0 −1 2 −1

0 0 −1 1







The nodal forces are

F =



1, 1, 1,



from (A.26, A.27). Notice that for the end node, j = 4, there is no additional term

from F

in (A.27), since the end of the bar is unloaded.

Substituting into (A.28) and solving for u, we obtain

u =

16EA

{3.5, 6, 7.5, 8}

and hence the end displacement is

∗

(L) = u

2EA

A.2.4 The Rayleigh-Rit z approach

The structural mechanics arguments of §A.2.1 has the advantage of being conceptu-

ally simple. The structure is essentially represented by a system of springs and the

properties of these springs are determined using the elementary concepts of Hooke’s

law, as applied to the axial loading of a uniform bar. Notice however that we had to

make a decision as to how to distribute the continuous axial loading p(x) between the

nodes and we developed the theory only for the simple case where the cross-sectional

area A and Young’s modulus E are indpendent of x.

For more general cases, the structural mechanics formulation can appear rather

arbitrary and to avoid this, the stationary potential energy principle is used to develop

the corresponding vectors and matrices. This is equivalent to the use of the Rayleigh-

Ritz method in combination with a suitable discrete approximation function, such as

the piecewise linear function of Figure A.2.

Following equation (A.1), we deﬁne the approximation

∗

(x) =

∑

i=1

(x) , (A.29)

where v

(x) is the piecewise linear shape function of equation (A.16). In the i-th

element (x

i−1

<x< x

), this gives

∗

(x) = u

i−1



−x

∆



+ u



x −x

i−1

∆



(A.30)

572 A The Finite Element Method

and hence the longitudinal strain is

∂

∗

∂



−u

i−1

∆



The strain energy density (2.32) can be written in terms of strain using Hooke’s law,

giving

E(u

−u

i−1

)

∆

The total strain energy in the i-th element is therefore given by equation (3.32) as

ZZZ

dV =

i−1

E(x)(u

−u

i−1

)

∆

A(x)dx

−u

i−1

)

∆

i−1

E(x)A(x)dx .

If there are element nodal forces F

i−1

at x

i−1

, the corresponding potential

energy will be

Ω

= −F

i−1

−F

(A.31)

and the total potential energy is

= U

Ω

−u

i−1

)

∆

i−1

E(x)A(x)dx −F

i−1

−F

The principle of stationary potential energy then gives

∂Π

∂

= 0 ;

∂Π

∂

i−1

= 0

and hence



1 −1

−1 1



i−1





i−1



, (A.32)

where

∆

i−1

E(x)A(x)dx . (A.33)

Notice that equation (A.32) is similar in form to (A.22), with an element stiffness

matrix

= k



1 −1

−1 1



. (A.34)

In the special case where E(x),A(x) are independent of x, this reduces to (A.23),

as we should expect. Notice however that the Rayleigh-Ritz method automatically

selects an appropriate approximation for the element stiffness in the case where E

and A are not constant.

If instead of element nodal forces F

i−1

we have a possibly variable distributed

load p(x) per unit length, the potential energy of the load will be

A.2 Axial loading 573

Ω

= −

i−1

p(x)u

∗

(x)dx

= −

i−1

∆

i−1

p(x)(x

−x)dx −

∆

i−1

p(x)(x −x

x−1

)dx ,

from equation (A.30). Comparing this result with equation (A.31), we see that the

distributed load is equivalent to a pair of element nodal forces equal to

i−1

∆

i−1

p(x)(x

−x)dx (A.35)

∆

i−1

p(x)(x −x

x−1

)dx . (A.36)

In the special case where p(x) = p

is independent of x, equations (A.35, A.36) give

i−1

= F

= p

∆

/2, as assumed in §A.2.3. For the more general case, they deﬁne an

algorithm for sharing out the distributed load p(x) between adjacent nodes according

to the lever rule — e.g., a force F at the point x in the range x

j− 1

<x< x

contributes

F(x−x

i−1

∆

to F

and F(x

−x)/

∆

to F

i−1

The global stiffness matrix can now be assembled by superposing the element

stiffness matrices (A.34), following the pattern of (A.23). The resulting matrix K is

deﬁned by

(EA)

−

+ (EA)

∆

; i = j 6= N

(EA)

−

∆

; i = j = N

= −

(EA)

−

∆

; i = j −1

= −

(EA)

∆

; i = j + 1

= 0 ; |i − j| > 1 ,











(A.37)

where

(EA)

−

∆

j−1

E(x)A(x)dx ; (EA)

∆

j+1

E(x)A(x)dx (A.38)

are the mean values of E(x)A(x) in the element to the left and right respectively of

node j.

Also, each nodal force for the complete system is the sum of the corresponding

elemental nodal forces from the two adjacent elements, given by equations (A.35,

A.36). We therefore have

∆

j−1

p(x)(x −x

j− 1

)dx +

∆

j+1

p(x)(x

j+1

−x)dx , (A.39)

for j 6= N and

∆

N−1

p(x)(x −x

N−1

)dx + F

. (A.40)

574 A The Finite Element Method

Example A.3

Figure A.7 shows a vertical bar of length L supported at the top, x = 0, and loaded

only by its own weight. The cross-sectional area of the bar varies according to the

equation

A(x) = A



1 −



where x is the vertical distance from the support. Estimate the displacement at the

free end using the ﬁnite element method with four equal length elements. The mate-

rial has density

and Young’s modulus E.

For this problem, the element length is

∆

= L/4. We ﬁrst evaluate the four inte-

grals

∆

E(x)A(x)dx =

4EA

L/4



1 −



dx =

15EA

∆

E(x)A(x)dx =

4EA

L/2

L/4



1 −



dx =

13EA

∆

E(x)A(x)dx =

4EA

3L/4

L/2



1 −



dx =

11EA

∆

E(x)A(x)dx =

4EA

3L/4



1 −



dx =

9EA

Substituting these results into equations (A.38, A.37), we obtain the global stiff-

ness matrix as

K =







28 − 13 0 0

−13 24 −11 0

0 −11 20 −9

0 0 −9 9







A(x)

Figure A.7