Banner A. The Calculus Lifesaver: All the Tools You Need to Excel at Calculus
Подождите немного. Документ загружается.


136 • Trig Limits and Derivatives
(once for each term) to show that they both go to 0. I suggest you try it as
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x + 2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
an exercise now. In practice, most mathematicians would automatically write
down the answer 0, having established the general principle that
lim
x→∞
sin(anything)
x
α
= 0
for any positive exponent α, and similarly when sine is replaced by cosine. In
any case, the above limit works out to be
1 + 0 + 0 + 0
1 − 0 − 0
×
3
2
=
3
2
.
Finally, let’s return to the example
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x + 2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
lim
x→0
x sin
5
x
,
which was mentioned at the beginning of this chapter. As we saw then, this
does belong to the large case even though the limit is taken as x → 0, because
5/x is a large number (positive or negative) when x is near 0. So the best we
can do is to use the sandwich principle, combined with the fact that the sine
of any number is between −1 and 1. In particular, we have
−1 ≤ sin
5
x
≤ 1
for any x. Now the temptation is to multiply by x:
−x ≤ x sin
5
x
≤ x.
Unfortunately, this is only true for x > 0. For example, if x = −2, then the
leftmost part of the inequality would be 2 and the rightmost part would be
−2, which is crazy. So let’s worry about the right-hand limit first:
lim
x→0
+
x sin
5
x
.
Now we can use the above inequalities and note that both −x and x go to 0
as x → 0
+
, so the sandwich principle applies and the above limit is 0. As for
the left-hand limit (as x → 0
−
), now we start off with the same inequality for
sin(5/x) and multiply it by x, but this time we have to reverse the inequalities
since x is negative. In particular, when x < 0, we have
−x ≥ x sin
5
x
≥ x.
It doesn’t matter much, though—the outer quantities still go to 0 as x → 0
−
,
so the middle quantity also goes to 0. Since the left-hand and right-hand
limits are both 0, so is the two-sided limit; we have proved that
lim
x→0
x sin
5
x
= 0.
(This example is very similar to the one on page 52.)

Section 7.1.4: The “other” case • 137
7.1.4 The “other” case
Consider the limit
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x + 2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
lim
x→π/2
cos(x)
x −
π
2
.
The trig function, cosine in this case, is being evaluated near π/2. This is
neither small nor large, so apparently the previous cases don’t apply. If you
just plug in x = π/2, you get the indeterminate form 0/0, which sucks. If you
know your trig identities, though, you’re golden. Here’s why.
A good general principle when dealing with a limit involving x → a for
some a 6= 0 is to shift the problem to 0 by substituting t = x − a. So
in the above limit, set t = x − π/2. Then when x → π/2, you can see that
t → 0. Also, x = t + π/2, so we have
lim
x→π/2
cos(x)
x −
π
2
= lim
t→0
cos
t +
π
2
t
.
Notice that we still need to know the behavior of cosine near π/2 (as you
can see by setting t near 0 and looking what you’re taking cosine of!); the
substitution hasn’t changed that fact. Now, this is where you need to know
the following trig identity from Section 2.4 of Chapter 2:
cos
π
2
− x
= sin(x).
In our limit, we have cos(
π
2
+ t), so we need to apply the above trig identity
with x replaced by −t in order for it to be useful. We get
cos
π
2
+ t
= sin(−t).
The other thing we need to remember is that sine is an odd function, so in
fact
cos
π
2
+ t
= sin(−t) = −sin(t).
Now we can put this into the limit and finish the problem. All in all,
lim
x→π/2
cos(x)
x −
π
2
= lim
t→0
cos
t +
π
2
t
= lim
t→0
−sin(t)
t
= −1.
Not so easy, but knowing the trig identities certainly helps in situations like
these.
7.1.5 Proof of an important limit
We’ve been using the following limit over and over again in this chapter, and
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
now it’s time to prove it:
lim
x→0
sin(x)
x
= 1.
The proof has to rely on the geometry of right-angled triangles, since that’s
where the sine function comes from. Let’s start with the right-hand limit (as
x → 0
+
). Once we get that, we’ll see that the two-sided limit is pretty easy.
So, we’ll start off by assuming that x is near 0 but positive. Let’s draw a
wedge OAB of a circle of radius 1 unit with angle x:
138 • Trig Limits and Derivatives
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f(
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x + 2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f(x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
1
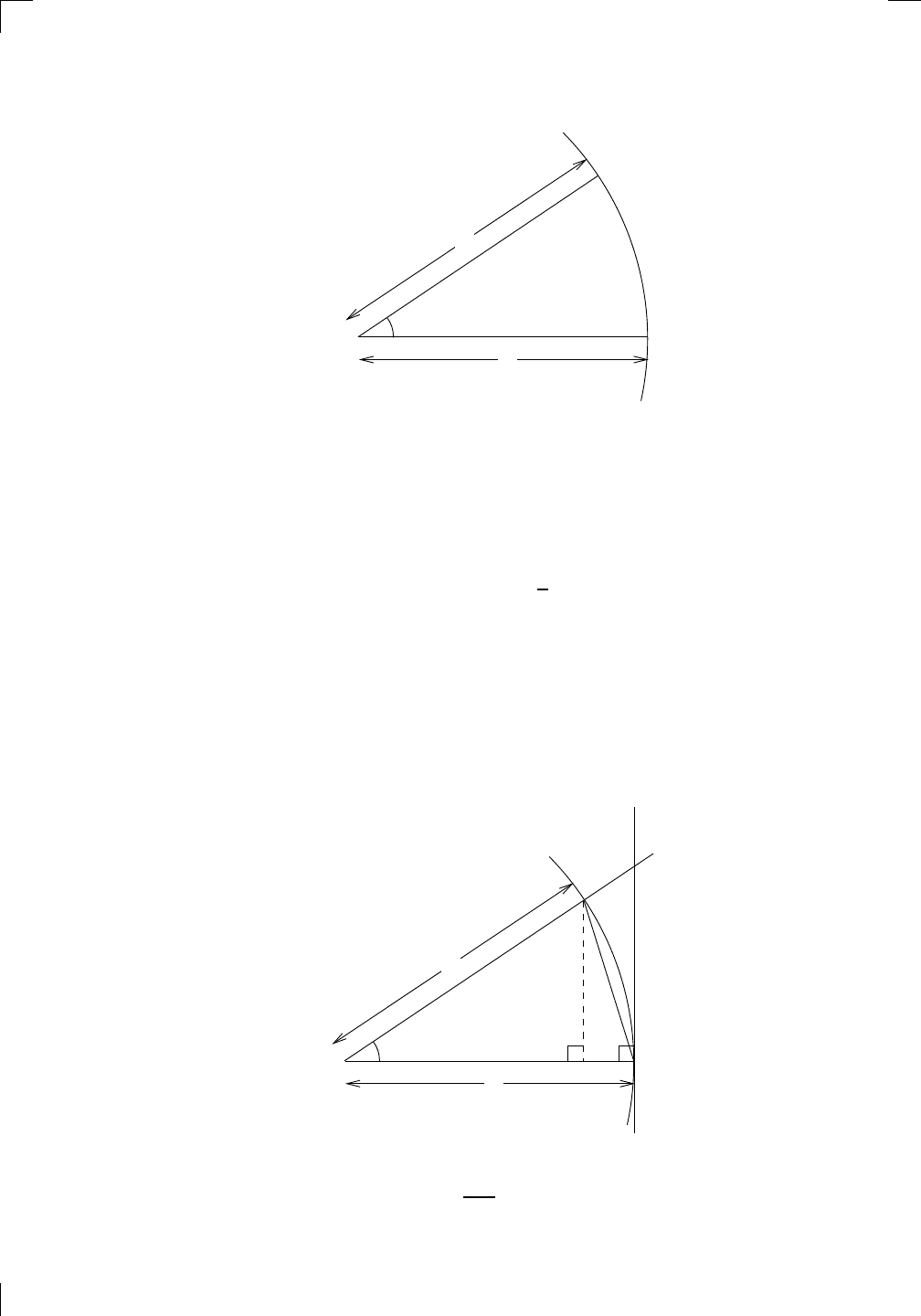
We’re going to doctor this figure a little, but first, a question: what is the
area of this wedge? Imagine that the wedge is a slice from a big pizza. The
pizza has radius 1 unit, so its area is πr
2
= π square units. Now, how much
of the pizza do we have in our slice? The whole pizza has 2π radians of angle,
while the slice has x radians, so the slice accounts for x/2π of the pizza. The
area is therefore (x/2π) × π, or simply x/2 square units. That is,
area of wedge OAB =
x
2
square units.
(This is a special case of the general formula: the area of a wedge of angle x
radians in a circle of radius r units is simply xr
2
/2 square units.)
Now let’s do a few things to the figure. First, we’ll draw in the line AB.
Then we’ll drop a perpendicular from A down to the line OB; call the base
point C. We’ll also extend the line OA out a little bit, and finally draw the
tangent line to the circle at the point B. That tangent line intersects the
extended line OA at a point D. After we do all that, we get the following
picture:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x + 2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f (x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f (x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f(x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
1
C
D
sin(x)
tan(x)
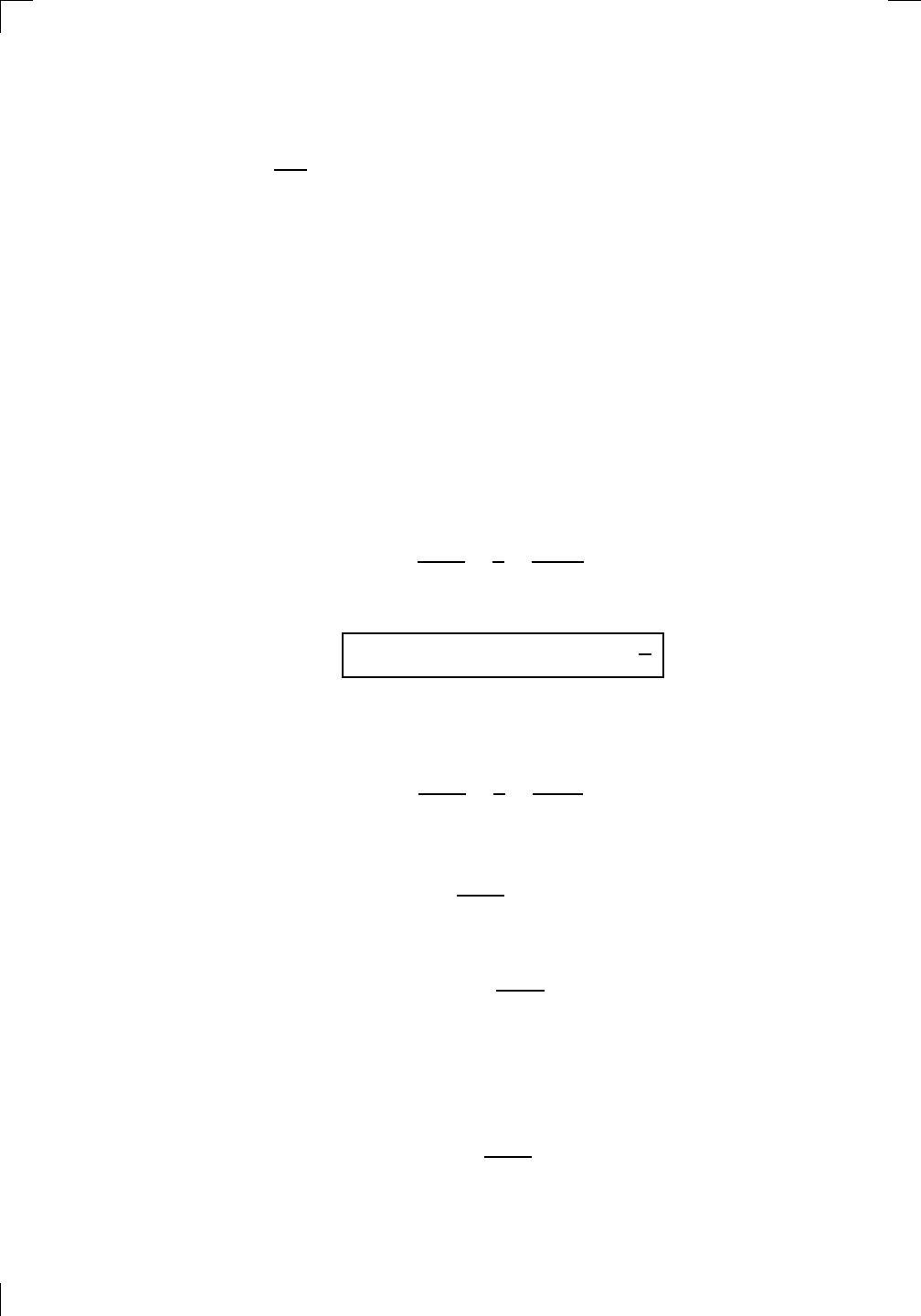
I marked the lengths of AC and DB on the diagram. To see how I worked out
these lengths, note that sin(x) =
|AC|
|OA|
(remember, |AC| means “the length of
Section 7.1.5: Proof of an important limit • 139
the segment AC”). Since |OA| = 1, we have |AC| = sin(x). Also, we have
tan(x) =
|DB|
|OB|
, and |OB| = 1, so |DB| = tan(x).
I want to focus attention on three objects. One is the original wedge; we
already found that the area of this is x/2 square units. Let’s also look at the
triangles ∆OAB and ∆OBD. The base of ∆OAB is OB, which has length 1
unit. The height is AC, which has length sin(x) units. So the area of ∆OAB
is half the base times the height, or sin(x)/2 square units. As for ∆OBD, its
base OB has length 1 unit and its height DB has length tan(x) units, so the
area of ∆OBD is tan(x)/2 square units. The crucial observation is that
∆OAB is contained in the wedge OAB which is contained in ∆OBD.
This means that the area of ∆OAB is less than the area of the wedge OAB,
which itself is less than the area of ∆OBD:
area of ∆OAB < area of wedge OAB < area of ∆OBD.
We know all three of these quantities in terms of the variable x; substituting
them in, we have
sin(x)
2
<
x
2
<
tan(x)
2
.
Multiplying this by 2, we get a really nice inequality which is worth remem-
bering:
sin(x) < x < tan(x) for 0 < x <
π
2
.
Now we can find our limit. Let’s first take reciprocals of the nice inequality.
Remember, this forces us to switch the less-than signs to greater-than signs.
Writing tan(x) = sin(x)/ cos(x), the reciprocal inequality is
1
sin(x)
>
1
x
>
cos(x)
sin(x)
.
Finally, multiply by the positive quantity sin(x) to see that
1 >
sin(x)
x
> cos(x).
If it creeps you out to write it backward like this, you can always rewrite it as
cos(x) <
sin(x)
x
< 1.
(Remember, this is true for any x between 0 and π/2.) Now we use the
sandwich principle: since cos(0) = 1 and y = cos(x) is continuous, we know
that lim
x →0
+
cos(x) = 1. Also, lim
x →0
+
(1) = 1; so the quantity sin(x)/x is squished
between cos(x) and 1, both of which tend to 1 as x → 0
+
. By the sandwich
principle,
lim
x→0
+
sin(x)
x
= 1
as well. So we’ve got our right-hand limit.
140 • Trig Limits and Derivatives
We still have to deal with the left-hand limit and show that
lim
x→0
−
sin(x)
x
= 1.
If we can do it, then we will have proved that both the left-hand and right-
hand limits are 1, so the two-sided limit is also 1 and we’ll be done.
To prove that the left-hand limit is 1, set t = −x. Then when x is a small
negative number, t is a small positive number. In math symbols, we can say
that as x → 0
−
, we have t → 0
+
. So the above limit can be written as
lim
t→0
+
sin(−t)
−t
.
Now we know that sin(−t) = −sin(t) (since sine is an odd function), so we
can simplify the limit down to
lim
t→0
+
−sin(t)
−t
= lim
t→0
+
sin(t)
t
.
We’ve already seen that this limit is 1 (well, with x instead of t, but so what?),
so we’re all done.
Before we move on to differentiating trig functions, I want to consider the
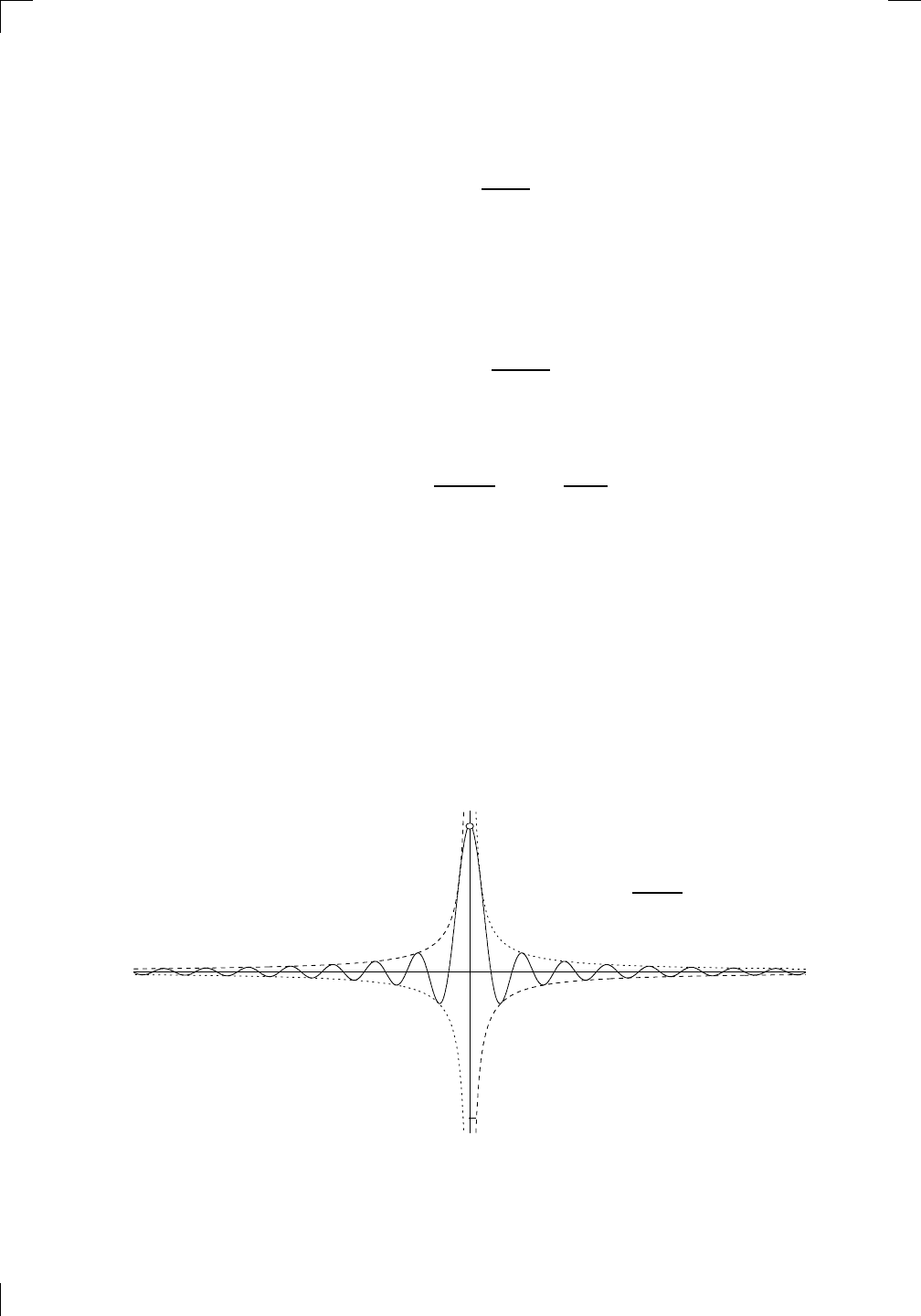
graph of f(x) = sin(x)/x. The argument for the left-hand limit has in fact
shown that f is an even function (can you see why?). This means that the
y-axis acts as a mirror for the graph of y = f(x). If you look back at page 51,
you can see that we have already drawn the graph of y = f(x) when x > 3.
We didn’t do x ≤ 3 since we didn’t know what happens. Now we know:
as x → 0, the quantity f (x) = sin(x)/x → 1. In fact, we have shown that
sin(x)/x lies between cos(x) and 1. This allows us to extend the graph down
to x > 0. Finally we use the evenness of f to give the complete graph of
y = sin(x)/x in all its glory (note the different scales on the x- and y-axes):
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f(
x)
a
y =
|
x|
x
1
−
1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f (t))
(u, f (u))
time
y
t
u
y
x
(x, f (x))
y = |x|
(z, f (z))
z
y = f (x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f (x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f(x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
The graphs of the envelope functions y = 1/x and y = −1/x are shown as
dotted curves. Also, the x-intercepts are at all the multiples of π except for

Section 7.2: Derivatives Involving Trig Functions • 141
0. Finally, as you can see, the function isn’t continuous at x = 0 since it isn’t
defined there. However, if we define the function g by g(x) = sin(x)/x if x 6= 0
and g(0) = 1, then we have effectively filled in the open circle at (0, 1) in the
above picture, and the function g is continuous.
7.2 Derivatives Involving Trig Functions
Now, time to differentiate some functions. Let’s start off by differentiating
sin(x) with respect to x. To do this, we’re going to use two of the limits from
Section 7.1.2 above:
lim
h→0
sin(h)
h
= 1 and lim
h→0
1 − cos(h)
h
= 0.
(OK, so I changed x to h, but no matter—the h is a dummy variable anyway
and could be replaced by any letter at all.) Anyway, with f(x) = sin(x), let’s
differentiate:
f
0
(x) = lim
h→0
f(x + h) − f (x)
h
= lim
h→0
sin(x + h) − sin(x)
h
.
Now what? Well, you should remember the formula
sin(A + B) = sin(A) cos(B) + cos(A) sin(B);
if not, you’d better look at Chapter 2 again. Anyway, we want to replace A
by x and B by h, so we have
sin(x + h) = sin(x) cos(h) + cos(x) sin(h).
Inserting this in the above limit, we get
f
0
(x) = lim
h→0
sin(x) cos(h) + cos(x) sin(h) − sin(x)
h
.
All that’s left is to group the terms a little differently and do a bit of factoring;
we get
f
0
(x) = lim
h→0
sin(x)(cos(h) − 1) + cos(x) sin(h)
h
= lim
h→0
sin(x)
cos(h) − 1
h
+ cos(x)
sin(h)
h
.
Notice that we separated as much x-stuff as we could from h-stuff. Now we
actually have to take the limit as h → 0 (not as x → 0!). Using the two limits
from the beginning of this section, we get
f
0
(x) = sin(x) × 0 + cos(x) × 1 = cos(x).
That is, the derivative of f(x) = sin(x) is f
0
(x) = cos(x), or in other words,
d
dx
sin(x) = cos(x).
142 • Trig Limits and Derivatives
Now you should try to repeat the argument but this time with f(x) = cos(x).
You just need the identity
cos(A + B) = cos(A) cos(B) − sin(A) sin(B)
from Chapter 2. It’s a really good exercise, so try to do it now. If you’ve done
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangen
t at x = a
b
tangen
t at x = b
c
tangen
t at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
it correctly, you should see that
d
dx
cos(x) = −sin(x).
Anyway, it’s a piece of cake to get the derivatives of the other trig functions
now; you don’t need to use any limits. You can just use the quotient rule and
the chain rule. Let’s start with the derivative of y = tan(x). We can write
tan(x) as sin(x)/ cos(x), so if we set u = sin(x) and v = cos(x), then y = u/v.
We just worked out that du/dx = cos(x) and dv/dx = −sin(x). Using the
quotient rule, we get
dy
dx
=
v
du
dx
− u
dv
dx
v
2
=
cos(x)(cos(x)) − sin(x)(−sin(x))
cos
2
(x)
.
The numerator of this last fraction is just cos
2
(x) + sin
2
(x), which is always
equal to 1; so the derivative is just
dy
dx
=
1
cos
2
(x)
= sec
2
(x).
We’ve just shown that
d
dx
tan(x) = sec
2
(x).
Now let’s calculate the derivative of y = sec(x). Here we are able to write
y = 1/ cos(x), so you might think that the quotient rule is best. Indeed, you
can do it by using the quotient rule, but the chain rule is nicer. If u = cos(x),
then y = 1/u. We can differentiate both of these things: dy/du = −1/u
2
, and
du/dx = −sin(x). By the chain rule,
dy
dx
=
dy
du
du
dx
=
−
1
u
2
(−sin(x)) =
sin(x)
cos
2
(x)
,
where we had to replace u by cos(x) in the last step. Actually, you can tidy
up the answer as follows:
sin(x)
cos
2
(x)
=
1
cos(x)
sin(x)
cos(x)
= sec(x) tan(x),
so we’ve shown that
d
dx
sec(x) = sec(x) tan(x).
As for y = csc(x), that should be written as 1/ sin(x). Once again, it’s
best to use the chain rule, letting u = sin(x) and writing y = 1/u. But I

Section 7.2.1: Examples of differentiating trig functions • 143
know you want to use the quotient rule, since it’s a quotient, even though it’s
inferior. You just don’t believe me. Well, check this. To use the quotient rule
on y = 1/ sin(x), we’ll actually let u = 1 and v = sin(x). Then du/dx = 0
and dv/dx = cos(x). By the quotient rule,
dy
dx
=
v
du
dx
− u
dv
dx
v
2
=
sin(x)(0) − 1(cos(x))
sin
2
(x)
= −
cos(x)
sin
2
(x)
.
OK, it wasn’t that bad, but the chain rule is still nicer. Anyway, by splitting
up the answer as we just did for the derivative of y = sec(x), you should be
able to simplify it to get
d
dx
csc(x) = −csc(x) cot(x).
Finally, consider y = cot(x), which of course can be written as either
y = cos(x)/ sin(x) or y = 1/ tan(x). You could use the quotient rule on
y = cos(x)/ sin(x), or now that we know the derivative of tan(x), you could
use the chain rule (or even the quotient rule) on y = 1/ tan(x). You could even
write cot(x) as the product cos(x) csc(x) and use the product rule. Whichever
way you do it, you should get
d
dx
cot(x) = −csc
2
(x).
You should learn all six boxed formulas by heart. Notice that the three
cofunctions (cos, csc, cot) all have minus signs in front of them, and the
derivatives are the co- versions of the regular ones. For example, the derivative
of sec(x) is sec(x) tan(x), so throwing a “co” in front of everything and also
putting in a minus sign, we get that the derivative of csc(x) is −csc(x) cot(x).
The same is true for cos and cot, remembering (in the case of cos) that co-co-
sine is just the original sine function.
By the way, what is the second derivative of f(x) = sin(x)? We know
that f
0
(x) = cos(x), and so f
00
(x) is the derivative of cos(x), which we saw is
−sin(x). That is,
d
2
dx
2
(sin(x)) = −sin(x).
The second derivative of the function is just the negative of the original func-
tion. The same is true for g(x) = cos(x). This sort of thing doesn’t happen at
all with (nonzero) polynomials, since the derivative of a polynomial is a new
polynomial whose degree is one less than the original one.
7.2.1 Examples of differentiating trig functions
Now that you have some more functions to differentiate, you’d better make
sure you still know how to use the product rule, the quotient rule, and the
chain rule. For example, how would you find the following derivatives:
d
dx
(x
2
sin(x)),
d
dx
sec(x)
x
5
and
d
dx
(cot(x
3
))?
144 • Trig Limits and Derivatives
Let’s take them one at a time. If y = x
2
sin(x), then we can write y = uv
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangen
t at x = a
b
tangen
t at x = b
c
tangen
t at x = c
y = x
2
tangen
t
at x = −
1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
where u = x
2
and v = sin(x). Now we just need to set up our table:
u = x
2
v = sin(x)
du
dx
= 2x
dv
dx
= cos(x).
Using the product rule (see Section 6.2.3 in the previous chapter), we get
dy
dx
= v
du
dx
+ u
dv
dx
= sin(x) · (2x) + x
2
cos(x).
This would normally be written as 2x sin(x) + x
2
cos(x). Anyway, let’s do the
second example. If y = sec(x)/x
5
, this time we set u = sec(x) and v = x
5
so
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
that y = u/v. Our table looks like this:
u = sec(x) v = x
5
du
dx
= sec(x) tan(x)
dv
dx
= 5x
4
.
Whipping out the quotient rule leads to
dy
dx
=
v
du
dx
− u
dv
dx
v
2
=
x
5
sec(x) tan(x) − sec(x) · 5x
4
(x
5
)
2
=
sec(x)(x tan(x) − 5)
x
6
.
Note that we canceled out a factor of x
4
at the end. Now, moving on to the
third example, set y = cot(x
3
). Here we are dealing with a composition of
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
two functions, so we’d better use the chain rule. The first thing that happens
to x is that it gets cubed, so let u = x
3
. Then y = cot(u). Our table is
y = cot(u) u = x
3
dy
du
= −csc
2
(u)
du
dx
= 3x
2
.
By the chain rule, we have
dy
dx
=
dy
du
du
dx
= −csc
2
(u) · 3x
2
.
We can’t just leave that u term lying around—we need to replace it by x
3
.
Altogether, then, our derivative is −3x
2
csc
2
(x
3
).
Before we move on, I want to show you a neat trick. Suppose you have
y = sin(8x) and you want to find dy/dx. You could do it by using the chain
rule, setting u = 8x, so that y = sin(u). It’s an easy exercise (try it!) to show
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
that dy/dx = 8 cos(8x). Of course, there’s nothing special about the number
8; it could have been anything. So the general rule is that
d
dx
(sin(ax)) = a cos(ax)
for any constant a. Basically, if x is replaced by ax , then there is an
extra factor of a out front when you differentiate. This also works
for the other trig functions. For example, the derivative with respect to x
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
of tan(x) is sec
2
(x), so the derivative of tan(2x) is 2 sec
2
(2x). In the same
way, the derivative of csc(x) is −csc(x) cot(x), so the derivative of csc(19x) is
−19 csc(19x) cot(19x). This saves you the trouble of using the chain rule in
this easy case.

Section 7.2.2: Simple harmonic motion • 145
7.2.2 Simple harmonic motion
One place where trig functions appear naturally is in describing the motion
of a weight on a spring bouncing up and down. It turns out that if x is the
position of a weight on a spring at time t, taking upward as positive, then a
possible equation for x is something like x = 3 sin(4t). The numbers 3 and 4
might change, and the “sin” might be a “cos,” but that’s the basic idea. The
equation is reasonable—after all, cosine keeps bouncing back and forth, and
so does the weight. This sort of motion is called simple harmonic motion.
So, if x = 3 sin(4t) is the displacement of the weight from its starting
point, what are the velocity and the acceleration of the weight at time t? All
we have to do is differentiate. We know that v = dx/dt, so we just have to
differentiate 3 sin(4t) with respect to t. We could use the chain rule, but it’s
simpler to use the observation at the end of the previous section. Indeed, to
differentiate sin(4t) with respect to t, we just observe that the derivative of
sin(t) would be cos(t), so the derivative of sin(4t) is 4 cos(4t). (Don’t forget
that factor of 4 out front!) All in all, we have
v =
d
dt
(3 sin(4t)) = 3 × 4 cos(4t) = 12 cos(4t).
Now we can repeat the exercise for acceleration, which is given by dv/dt, using
the same technique:
a =
dv
dt
=
d
dt
(12 cos(4t)) = −12 × 4 sin(4t) = −48 sin(4t).
Notice that the acceleration—which of course is the second derivative of the
displacement—is basically the same as the displacement itself, except that
there’s a minus out front and the coefficient is different (48 instead of 3).
The minus means that the acceleration is in the opposite direction from the
displacement. In fact, we have shown that
a = −16x,
since 48 = 3 × 16. Now let’s interpret this equation by examining the motion
of the weight a little more closely.
The position x is given by x = 3 sin(4t), with the understanding that the
rest position of the weight is at x = 0. Now, if we multiply the inequality
−1 ≤ sin(4t) ≤ 1 (which is true for all t) by 3, we get −3 ≤ 3 sin(4t) ≤ 3. That
is, −3 ≤ x ≤ 3. So we can see that x is oscillating between −3 and 3. When
x is positive, the weight is above its rest position; then a is negative, which
is good: the acceleration is downward, as it should be. As x gets bigger and
bigger, the spring compresses even more, causing the weight to experience a
greater force and acceleration downward. Eventually the weight starts going
down, and after a little while x becomes negative. Then the weight is below
its rest position, so the spring is expanded and tries to pull the weight back
up. Indeed, when x is negative, a is positive, so the force is upward. The
following picture shows what’s going on:
