Banner A. The Calculus Lifesaver: All the Tools You Need to Excel at Calculus
Подождите немного. Документ загружается.


116 • How to Solve Differentiation Problems
It’s not hard to check that these equations are consistent. Differentiating
with respect to t, we see that dv/dt = −g, which is equal to a; and that
dx/dt = −gt + u, which is just v. So a = dv/dt and v = dx/dt after all. Also,
when t = 0, we see that v = u and x = h. This means that the initial velocity
is u and the initial height is h. Everything checks out.
Now, let’s look at an example of how to use the above formulas. Suppose
you throw a ball up from a height of 2 meters above the ground with a speed
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
of 3 meters per second. Taking g to be 10 meters per second squared, we want
to know five things:
1. How long does it take for the ball to hit the ground?
2. How fast is the ball moving when it hits the ground?
3. How high does the ball go?
4. If instead you throw the ball at the same speed but downward, how long
does the ball take to hit the ground?
5. In that case, how fast does it hit the ground?
In the original situation, we know that g = 10, the initial height h = 2, and
the initial velocity u = 3. This means that the above formulas become
a = −10, v = −10t + 3, and x = −
1
2
(10)t
2
+ 3t + 2 = −5t
2
+ 3t + 2.
For part 1, we need to find how long it takes for the ball to get to the ground.
This surely happens when its height is 0. So set x = 0 and let’s find t; we get
0 = −5t
2
+ 3t + 2. If you factor this quadratic as −(5t + 2)(t − 1), you can
see that the solution of our equation is t = 1 or t = −2/5. Clearly the second
answer is unrealistic—the ball can’t hit the ground before you even throw it!
So the answer must be t = 1. That is, the ball hits the ground 1 second after
we throw it.
For part 2, we need to find the speed at the time when the ball hits the
ground. No problem—we know that v = −10t + 3, and that the ball hits the
ground when t = 1. Plugging that in, we see that v = −10 + 3 = −7. So the
velocity of the ball when it hits the ground is −7 meters per second. Why
negative? Because the ball is going downward when it hits, and downward is
negative. The speed of the ball is just the absolute value of the velocity, or 7
meters per second.
To solve the third part, you have to realize that the ball reaches the top
of its path when its velocity is exactly 0. On the way up, the velocity is
positive; on the way down, the velocity is negative; it must be 0 when it’s
changing from up to down. So, when is v equal to 0? We just need to solve
−10t + 3 = 0. The answer is t = 3/10. That is, the ball reaches the top of its
trajectory three-tenths of a second after we release it. How high is it then?
Just plug t = 3/10 into the formula x = −5t
2
+ 3t + 2 to see that
x = −5
3
10
2
+ 3
3
10
+ 2 =
49
20
.
That is, the ball reaches a height of 49/20 meters above the ground.
Section 6.5: Limits Which Are Derivatives in Disguise • 117
For the last two parts, you’re throwing the ball downward instead. We still
have g = 10 and the initial height h = 2, but what is the starting velocity u?
Don’t make the mistake of thinking that u is still 3! Since you are throwing
the ball downward, the initial velocity is negative. A speed of 3 meters per
second downward translates into an initial velocity u = −3. Omitting this
minus sign is a common mistake, so be warned. Anyway, our equations are
now
a = −10, v = −10t − 3, and x = −
1
2
(10)t
2
− 3t + 2 = −5t
2
− 3t + 2.
Notice how similar they are to the equations for the scenario when we threw
the ball upward. To solve part 4 of the problem, we need to find the time
the ball hits the ground. Just as we did in part 1, set x = 0; then we have
0 = −5t
2
−3t+2 = −(5t−2)(t+1). So t = 2/5 or t = −1. This time we reject
t = −1, since it’s before we threw the ball, so we must have t = 2/5. That
is, the ball hits the ground two-fifths of a second after we throw it. It makes
sense that it’s less than the time taken when we threw the ball up (which was
1 second), since the ball doesn’t have to go up and then down. For the final
part, we want to see how fast the ball is moving when it hits the ground; so put
t = 2/5 in the formula for velocity. We get v = −10(2/5) −3 = −4 −3 = −7.
Once again, the ball hits the ground with a speed of 7 meters per second.
Interesting that it doesn’t matter whether you throw the ball up or down (as
long as it’s from the same height and with the same speed in both cases): it
still hits the ground with the same speed, although the time taken to hit the
ground is different.
6.5 Limits Which Are Derivatives in Disguise
That’s enough motion for now. Consider how you’d find the following limit:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
lim
h→0
5
√
32 + h − 2
h
.
It looks pretty hopeless. Even the trick of multiplying by the conjugate-type
expression
5
√
32 + h +2 doesn’t work because it’s a 5th root, not a square root
(try it and see for yourself!). So let’s take a break from this and consider a
related limit:
lim
h→0
5
√
x + h −
5
√
x
h
.
Note that h, not x, is the dummy variable here. Now this limit looks pretty
difficult too, but perhaps it rings a bell. It’s pretty similar to the limit in our
formula
lim
h→0
f(x + h) − f (x)
h
= f
0
(x).
All you have to do is set f (x) =
5
√
x, and note that f
0
(x) =
1
5
x
−4/5
. (Here
we wrote
5
√
x as x
1/5
in order to find the derivative.) The derivative equation
becomes
lim
h→0
5
√
x + h −
5
√
x
h
=
1
5
x
−4/5
.
118 • How to Solve Differentiation Problems
So the limit on the left is a derivative in disguise! We had to create a function
f and differentiate it to solve the limit.
Now we can return to the original limit
lim
h→0
5
√
32 + h − 2
h
.
This is actually a special case of the limit
lim
h→0
5
√
x + h −
5
√
x
h
=
1
5
x
−4/5
,
which we just worked out. If you set x = 32 in this limit, you get
lim
h→0
5
√
32 + h −
5
√
32
h
=
1
5
× 32
−4/5
.
Since
5
√
32 = 2 and 32
−4/5
= 1/16, we have shown that
lim
h→0
5
√
32 + h − 2
h
=
1
5
× 32
−4/5
=
1
5
×
1
16
=
1
80
.
Make no mistake: this is hard. There is a double disguise here: not only
are we dealing with a derivative, we’re actually evaluating the derivative at a
particular point (32 in this case). You’re better off generalizing the situation
first, then substituting the specific value of x. Here’s another example:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
lim
h→0
p
(4 + h)
3
− 7(4 + h) − 6
h
.
This one could be done by multiplying top and bottom by the conjugate, but
it’s also a derivative in disguise. Since we are dealing with 4+h, let’s try replac-
ing 4 by x. The first term in the numerator becomes
p
(x + h)
3
− 7(x + h).
This suggests that we might try setting f(x) =
√
x
3
− 7x. In Section 6.2.5
above, we saw that f
0
(x) = (3x
2
− 7)/2
√
x
3
− 7x, so the equation
lim
h→0
f(x + h) − f(x)
h
= f
0
(x)
becomes
lim
h→0
p
(x + h)
3
− 7(x + h) −
√
x
3
− 7x
h
=
3x
2
− 7
2
√
x
3
− 7x
.
Finally, if you put x = 4, and simplify everything (noticing that you have
√
x
3
− 7x =
√
64 − 28 =
√
36 = 6), you get
lim
h→0
p
(4 + h)
3
− 7(4 + h) − 6
h
=
3(4)
2
− 7
2(6)
=
41
12
.
If you get stuck on a limit, it might be a derivative in disguise. Telltale
signs are that the dummy variable is by itself in the denominator, and the

Section 6.6: Derivatives of Piecewise-Defined Functions • 119
numerator is the difference of two quantities. Even if this doesn’t happen,
you could still be dealing with a derivative in disguise; for example,
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
lim
h→0
h
(x + h)
6
− x
6
has the dummy variable in the numerator. No matter—just flip it over and
find this limit first:
lim
h→0
(x + h)
6
− x
6
h
.
To do this, set f(x) = x
6
, so that f
0
(x) = 6x
5
. We have
lim
h→0
(x + h)
6
− x
6
h
= lim
h→0
f(x + h) − f(x)
h
= f
0
(x) = 6x
5
.
Now just flip it over again and get
lim
h→0
h
(x + h)
6
− x
6
=
1
6x
5
.
We’ll see a few other examples of limits which are derivatives in disguise in
the future (in Chapters 9 and 17, to be precise). Keep your eyes peeled: many
limits are derivatives in disguise, and your job is to unmask them.
∗
6.6 Derivatives of Piecewise-Defined Functions
Consider the following piecewise-defined function f:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
f(x) =
(
1 if x ≤ 0,
x
2
+ 1 if x > 0.
Is this function differentiable? Let’s graph it and see:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
∗
Actually, if you use l’Hˆopital’s Rule (see Chapter 14), you often don’t even need to
recognize when a limit is a derivative in disguise.

120 • How to Solve Differentiation Problems
Looks pretty smooth—no sharp corners. In fact, it’s pretty obvious that the
function f is differentiable everywhere except perhaps at x = 0. To the left of
x = 0, the function f inherits its differentiability from the constant function
1, and to the right of x = 0, it inherits its differentiability from x
2
+ 1. The
question is, what happens at x = 0, the interface between the two pieces?
The first thing to check is that the function is actually continuous there.
You can’t have differentiability without continuity, as we saw in Section 5.2.11
of the previous chapter. To see that f is continuous at x = 0, we need to show
that lim
x → 0
f(x) = f (0). Well, we can see from the definition of f that f(0) = 1.
As for the limit, let’s break it up into left-hand and right-hand limits. For the
left-hand limit, we have
lim
x→0
−
f(x) = lim
x→0
−
(1) = 1,
since f(x) = 1 when x is to the left of 0. As for the right-hand limit,
lim
x→0
+
f(x) = lim
x→0
+
(x
2
+ 1) = 0
2
+ 1 = 1,
since f (x) = x
2
+1 when x is to the right of 0. So the left-hand limit equals the
right-hand limit, which means that the two-sided limit exists and is 1. This
agrees with f(0), so we have proved that f is continuous at x = 0. (Notice
that for both the left-hand and right-hand limits, you effectively just have to
substitute x = 0 into the appropriate piece of f to get the limit.)
We still need to show that f is differentiable at x = 0. To do this, we have
to show that the left-hand and right-hand derivatives match at x = 0 (see
Section 5.2.10 in the previous chapter to refresh your memory of left-hand
and right-hand derivatives). To the left of 0, we have f(x) = 1, so f
0
(x) = 0
in this case. It turns out that we can push it all the way up to x = 0 like this:
lim
x→0
−
f
0
(x) = lim
x→0
−
0 = 0.
This shows that the left-hand derivative of f at x = 0 is 0. (See Section A.6.10
of Appendix A for more details.) To the right of 0, we have f (x) = x
2
+ 1, so
f
0
(x) = 2x there. Again, we can push this down to x = 0:
lim
x→0
+
f
0
(x) = lim
x→0
+
2x = 2 × 0 = 0.
So the right-hand derivative of f at x = 0 is 2×0 = 0. Since the left-hand and
right-hand derivatives at x = 0 match, the function is differentiable there.
So, to check that a piecewise-defined function is differentiable at a point
where the pieces join together, you need to check that the pieces agree at the
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f (x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f (x)
join point (for continuity) and that the derivatives of the pieces agree at the
join point. Otherwise it’s not differentiable at the join point.
∗
If you have
more than two pieces, you have to check continuity and differentiability at all
the join points.
∗
Actually, this is only true if the left- and right-hand limits of the derivatives at the
join points exist and are finite. See Section 7.2.3 in the next chapter for an example of this.

Section 6.6: Derivatives of Piecewise-Defined Functions • 121
Let’s look at one more example of differentiating a piecewise-defined func-
tion. Suppose that
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
g(x) =
(
|x
2
− 4| if x ≤ 1,
−2x + 5 if x > 1.
Where is g differentiable? You might think that the only issue is at the join
point x = 1, but actually the absolute value makes life more complicated.
Remember, the absolute value function is really a piecewise-defined function
in disguise! In particular, |x| = x when x ≥ 0, but |x| = −x when x < 0. It
follows that
|x
2
− 4| =
(
x
2
− 4 if x
2
− 4 ≥ 0,
−(x
2
− 4) if x
2
− 4 < 0.
In fact, the inequality x
2
− 4 < 0 can be rewritten as x
2
< 4, which means
that −2 < x < 2. (Be careful to include the −2 < x bit as well as the more
obvious x < 2 bit!) So we can simplify this a little to get
|x
2
− 4| =
(
x
2
− 4 if x ≥ 2 or x ≤ −2,
−x
2
+ 4 if − 2 < x < 2.
Now, in the definition of g(x) above, the term |x
2
− 4| only appears when
x ≤ 1. So, we can throw everything together and remove the absolute values
for once and for all, rewriting g(x) as follows:
g(x) =
x
2
− 4 if x ≤ −2,
−x
2
+ 4 if − 2 < x ≤ 1,
−2x + 5 if x > 1.
So actually there are two join points: x = −2 and x = 1. Since the three
pieces making up g are differentiable everywhere, we know that g itself is
differentiable everywhere except perhaps at the join points. Let’s check the
join points one at a time, starting with x = −2. First, continuity. From the
left, we have
lim
x→(−2)
−
g(x) = lim
x→(−2)
−
x
2
− 4 = (−2)
2
− 4 = 0,
while from the right, we have
lim
x→(−2)
+
g(x) = lim
x→(−2)
+
−x
2
+ 4 = −(−2)
2
+ 4 = 0.
Since the limits are equal, g is continuous at x = −2. Now, let’s check the
derivatives: for the left-hand derivative, we have
lim
x→(−2)
−
g
0
(x) = lim
x→(−2)
−
2x = 2(−2) = −4,
whereas for the right-hand derivative, we have
lim
x→(−2)
+
g
0
(x) = lim
x→(−2)
+
−2x = 2(−2) = 4.
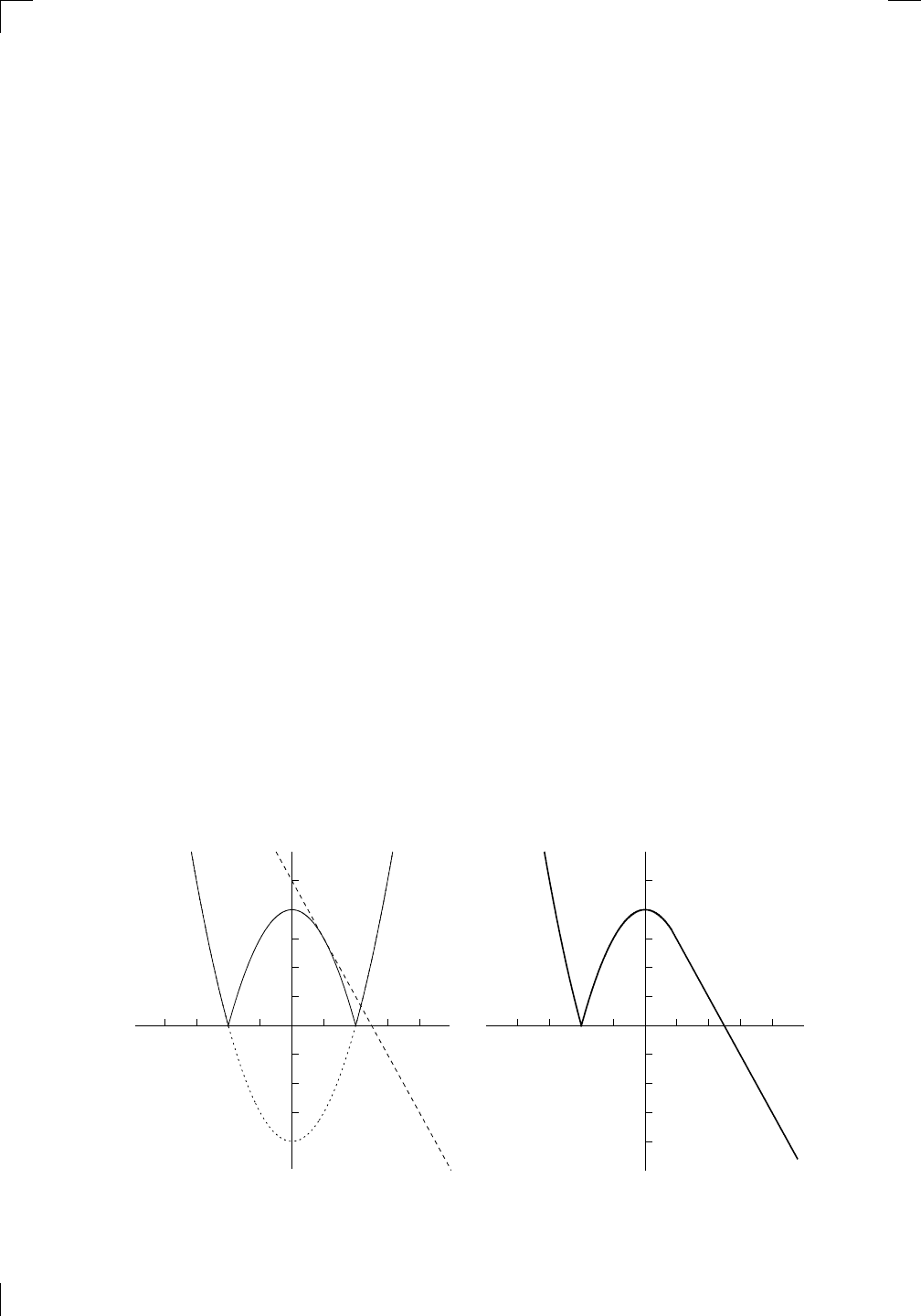
122 • How to Solve Differentiation Problems
Since these don’t match, the function g is not differentiable at x = −2.
How about at the other join point, x = 1? We repeat the exercise as
follows: left-continuity:
lim
x→1
−
g(x) = lim
x→1
−
−x
2
+ 4 = −(1)
2
+ 4 = 3.
Right-continuity:
lim
x→1
+
g(x) = lim
x→1
+
−2x + 5 = −2(1) + 5 = 3.
So they match, and g is continuous at x = 1. Now, left-differentiability:
lim
x→1
−
g
0
(x) = lim
x→1
−
−2x = −2(1) = −2.
As for right-differentiability:
lim
x→1
+
g
0
(x) = lim
x→1
+
−2 = −2.
Since they match, the function g is in fact differentiable at x = 1.
We’ve answered the original question, but let’s draw a graph anyway and
see what’s going on. To sketch the graph of y = |x
2
− 4|, let’s first graph
y = x
2
− 4. This is a parabola with x-intercepts at 2 and −2 (that’s where
y = 0) and y-intercept at −4. To get the absolute value, we take everything
below the x-axis and reflect it in the x-axis. The bit that we flip over is part
of the curve y = −x
2
+ 4. Finally, the line y = −2x + 5 has y-intercept 5 and
x-intercept 5/2, so that graph is not hard to draw either. In the following
two graphs, the left-hand graph shows all the functions that are ingredients
for making g(x), and the right-hand graph takes only what we need and is
purely the graph of y = g(x):
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f(x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f (t))
(u, f (u))
time
y
t
u
y
x
(x, f (x))
y = |x|
(z, f (z))
z
y = f (x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f (x)
1
1
2
−2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
Section 6.7: Sketching Derivative Graphs Directly • 123
It actually looks continuous everywhere and differentiable everywhere except
where there’s that sharp corner at (−2, 0). In particular, everything’s nice at
the join point x = 1, just as we calculated.
6.7 Sketching Derivative Graphs Directly
Suppose you have a graph of a function but not its equation, and you want
to sketch the graph of its derivative. Formulas and rules aren’t going to help
you here: instead, you need a good understanding of differentiation.
Here’s the basic idea. Imagine the graph of the function as a mountain,
and imagine that there is a little mountain-climber walking up and down the
graph from left to right. At each point of the climb, the climber calls out
how difficult he or she thinks the climb is. If the terrain is flat, the climber
calls out the number 0 for the degree of difficulty. If the terrain goes uphill,
the climber calls out a positive number; the steeper the climb, the higher the
number. If the terrain goes downhill, then the climb is actually easy, so the
degree of difficulty is negative. That is, the climber will call out a negative
number. The more downhill the terrain, the easier it is, so the number will
be more negative. (If it’s really steep going downhill, it might be difficult to
climb down safely, but it’s certainly easy to descend quickly!)
One important point: the height of the mountain itself isn’t relevant. It’s
only the steepness that matters. In particular, you could shift the whole graph
upward, and the climber would still be calling out the same degree of difficulty.
A consequence of this is that if you are drawing the graph of a derivative from
the graph of a function, the x-intercepts of the function are not important!
Let’s look at an example: sketch the derivative of the following fearsome-
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
looking function:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f (x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f (x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5 6
7
8 9
0
−1
−2
−3
−4
−5−6
y = f (x)
Don’t panic. Just draw a little mountain-climber at a whole bunch of
different points and imagine the climber shouting out the degree of difficulty
at each point. Then all you have to do is plot these degrees of difficulty on
another set of axes. Of particular interest are the points where the path is
flat; this can occur in a long flat section (such as between x = 5 and x = 6 in
the above graph), or at the top of a crest (such as at x = −5 or x = 1) or at
the bottom of a valley (such as at x = −2 or x = 3). You definitely want to
draw the mountain-climber there. Here’s what the graph of f looks like with
the climber in a bunch of positions:
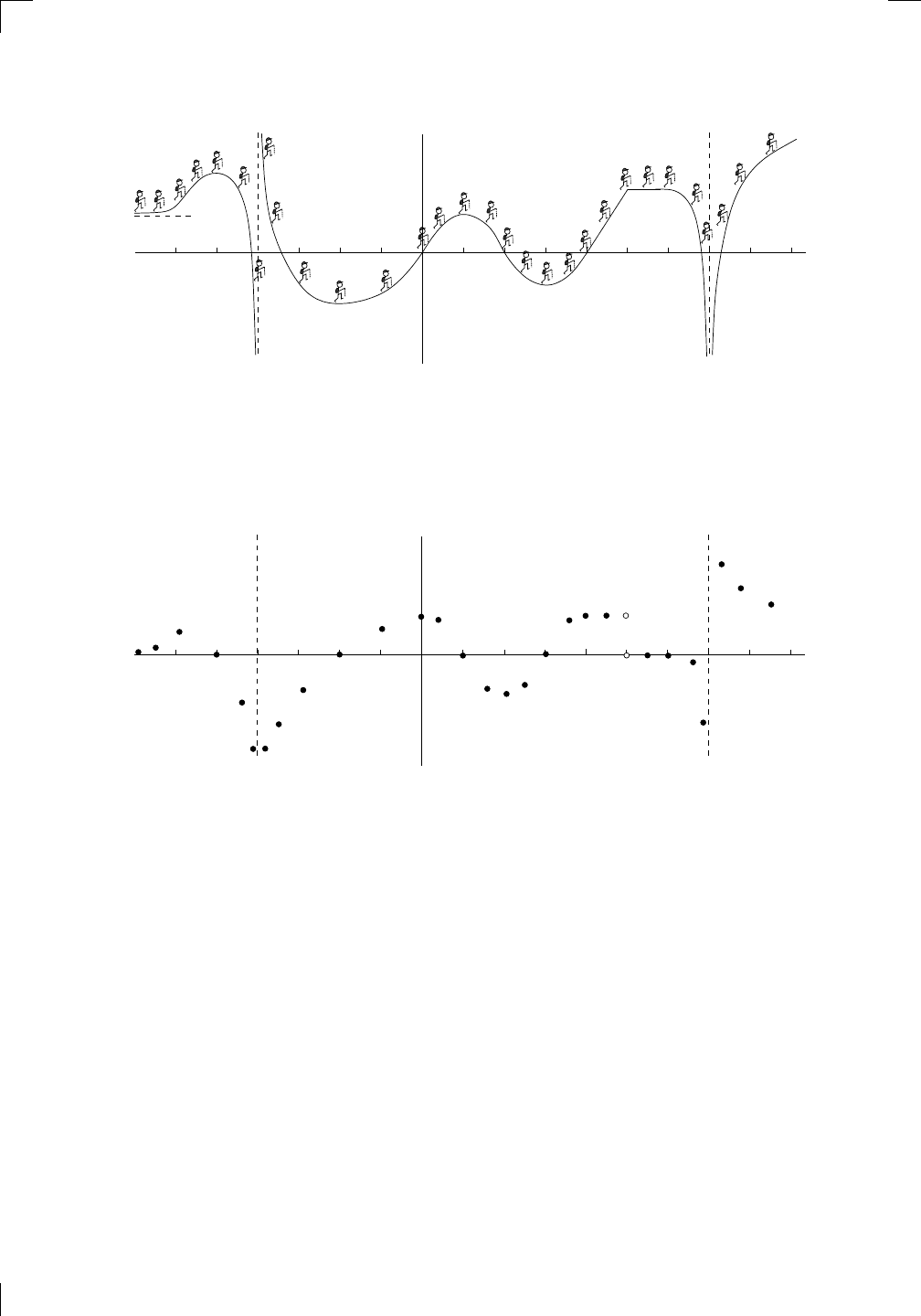
124 • How to Solve Differentiation Problems
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f (x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f (x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1 2
3
4 5
6
7
8
90−1−2
−3
−4
−5−6
y = f (x)
3
−3
Now let’s draw a set of axes for our graph of the derivative. Label the y-axis
as “degree of difficulty,” ranging from hard, down to flat at the origin, down
to easy. Then you should be able to pencil in some points based on what the
various copies of the little climber have shouted out. Remember, the climber
doesn’t care how high the mountain is, only how steep the climb is! Based
on this, you get the following points:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f (x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f (x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6 7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3−3
0
−1 2
easy
hard
flat
y = f
0
(x)
Here’s a detailed explanation of how we came to these conclusions:
• At the far left of the graph of y = f (x), the climber starts out going
only slightly uphill. So we’ll plot points of height a little above 0.
• Moving along to x = −6, the climber starts to go uphill, so the difficulty
has gone up, so the points get higher (more difficult).
• Then it starts getting a little easier, until when x = −5, the climber
has reached the top of the crest and it’s now flat. In particular, when
x = −5, the derivative has an x-intercept.
• After x = −5, the original curve starts to go downhill, first gently and
then more and more steely. This means that it’s getting easier and
easier, until it gets ridiculously easy. So the derivative also has a vertical
asymptote at x = −4.
• On the other side of the asymptote, the climb is also really easy—the
climber is going downhill, starting very steeply and then leveling out at
the valley when x = −2. So the vertical asymptote on the derivative
curve actually starts at −∞ (really easy) and climbs up to 0 at x = −2.
(The fact that there are x-intercepts between −5 and −4 and also be-
tween −4 and −3 is irrelevant. The x-intercepts of the original function
don’t matter.)
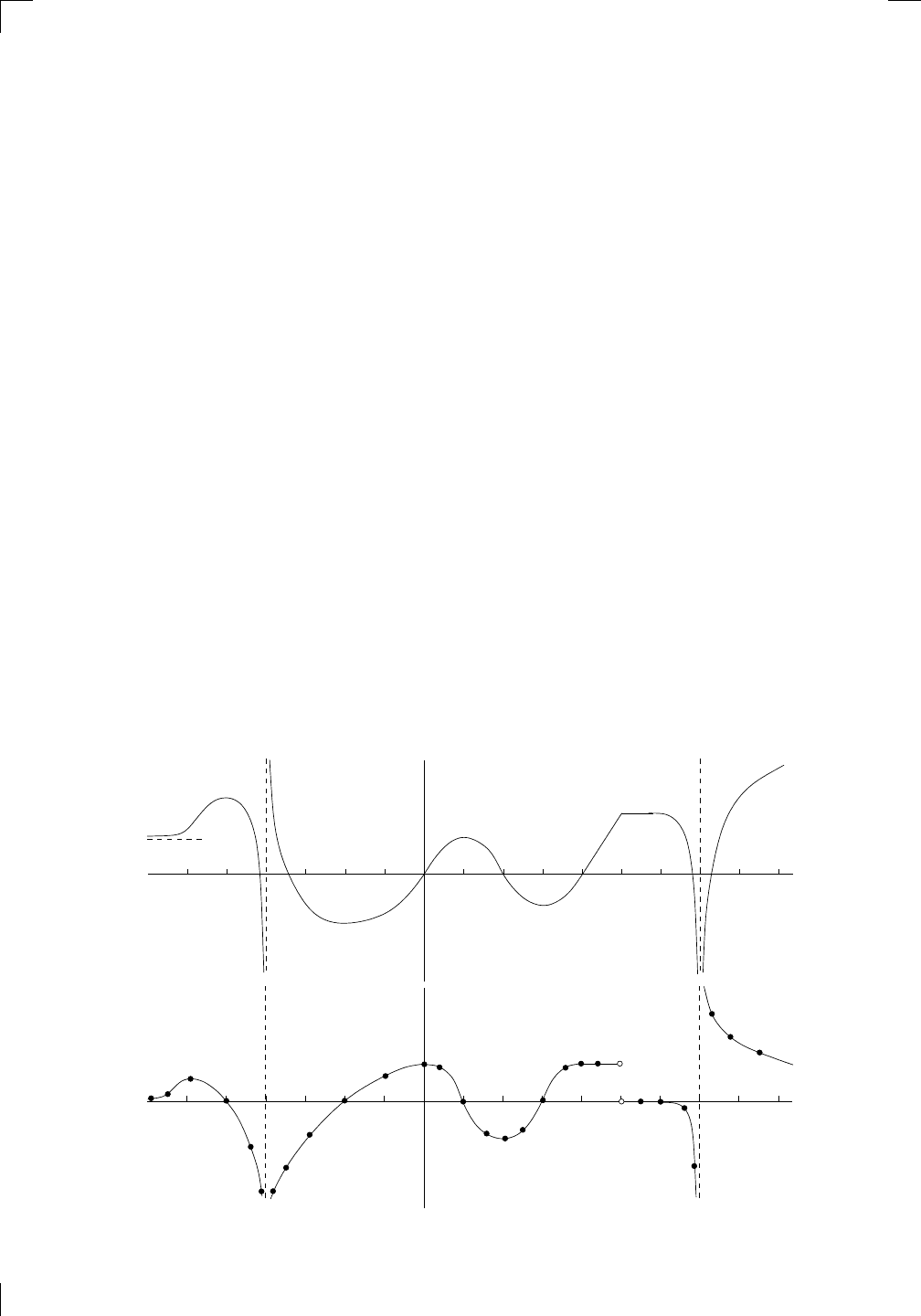
Section 6.7: Sketching Derivative Graphs Directly • 125
• After the bottom of the valley at x = −2, the climber has to go uphill
for a while, so it gets harder. After x = 0, though, it gets a little easier,
until he or she reaches the top of the hill at x = 1. This means that
the derivative curve goes up until x = 0, then comes back down to an
x-intercept at x = 1.
• The reverse happens on the way to the bottom of the valley at x = 3:
it gets easier and easier until x = 2, then it flattens out while still being
downhill. So the derivative curve goes down, reaches a minimum at
x = 2, then comes back up for an x-intercept at x = 3.
• From the bottom of the valley at x = 3, the climb gets steadily harder
until x = 4. Between x = 4 and x = 5, however, the climb is of uniform
difficulty, since the slope is constant. So the derivative curve increases
from x = 3 until x = 4, but then it stays at the same height (degree of
difficulty) between x = 4 and x = 5.
• At x = 5, the slope abruptly changes—it becomes flat without any
warning, then stays flat until x = 6. So the derivative curve must
jump down to 0 and stay there until x = 6. The derivative will have a
discontinuity at x = 5.
• After x = 6, the climber finds things easier and easier as the curve dips
down to the vertical asymptote at x = 7. The derivative curve also has
a vertical asymptote there.
• To the right of the vertical asymptote, the climb is extremely difficult,
but it does get a little easier as x moves up to 9. So the derivative curve
will start very high on the right side of x = 7 and then get a little lower
as the climb becomes easier.
Now, just connect the dots! Here are the graphs of y = f(x) and y = f
0
(x):
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f (x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f (x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4 5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3−3 0
−1 2
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f (x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f (x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8 9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0−1
2
1
2
