Banner A. The Calculus Lifesaver: All the Tools You Need to Excel at Calculus
Подождите немного. Документ загружается.

106 • How to Solve Differentiation Problems
with respect to x. You can let f(x) = 2x
3
− 3x + 1 and g(x) = x
5
− 8x
3
+ 2;
then you can write h as the quotient of f and g, or h(x) = f(x)/g(x). Now
here’s the quotient rule:
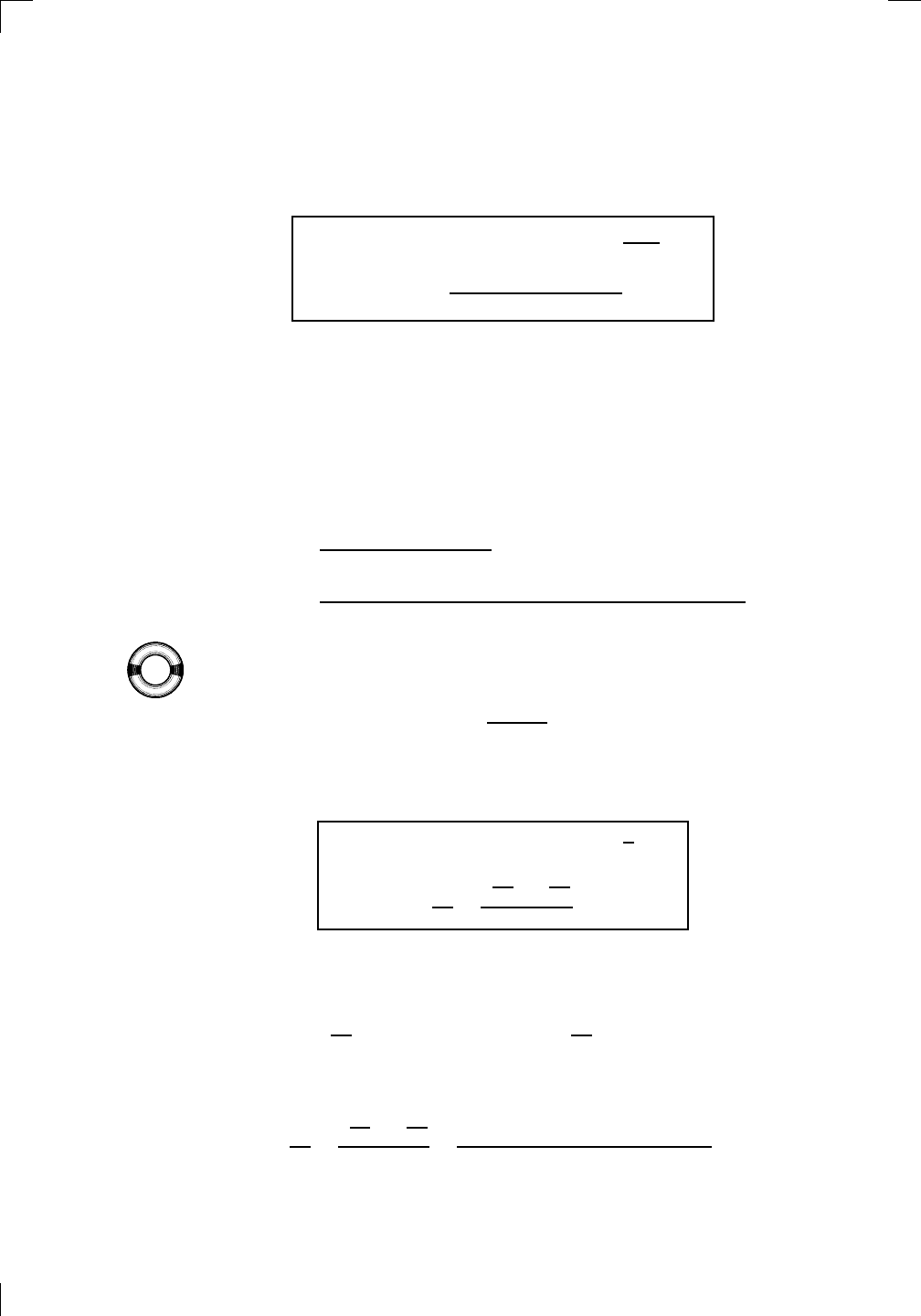
Quotient rule (version 1): if h(x) =
f(x)
g(x)
, then
h
0
(x) =
f
0
(x)g(x) − f(x)g
0
(x)
(g(x))
2
.
Notice that the numerator of the right-hand fraction is the same as the nu-
merator in the product rule, except with a minus instead of a plus. In our
example, we need to differentiate f and g and summarize our results:
f(x) = 2x
3
− 3x + 1 g(x) = x
5
− 8x
3
+ 2
f
0
(x) = 6x
2
− 3 g
0
(x) = 5x
4
− 24x
2
.
By the quotient rule, since h(x) = f (x)/g(x), we have
h
0
(x) =
f
0
(x)g(x) − f(x)g
0
(x)
(g(x))
2
=
(6x
2
− 3)(x
5
− 8x
3
+ 2) − (2x
3
− 3x + 1)(5x
4
− 24x
2
)
(x
5
− 8x
3
+ 2)
2
.
There’s also another version, just as there is in the case of the product rule.
If instead you are given that
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
y =
3x
2
+ 1
2x
8
− 7
,
and you want to find dy/dx, then start by writing u = 3x
2
+1 and v = 2x
8
−7,
so that y = u/v. Now we use:
Quotient rule (version 2): if y =
u
v
, then
dy
dx
=
v
du
dx
− u
dv
dx
v
2
.
Our summary box looks like this:
u = 3x
2
+ 1 v = 2x
8
− 7
du
dx
= 6x
dv
dx
= 16x
7
.
By the quotient rule,
dy
dx
=
v
du
dx
− u
dv
dx
v
2
=
(2x
8
− 7)(6x) − (3x
2
+ 1)(16x
7
)
(2x
8
− 7)
2
.
As you can see, quotients aren’t any harder than products (just a bit messier).
Section 6.2.5: Composition of functions via the chain rule • 107
6.2.5 Composition of functions via the chain rule
Suppose h(x) = (x
2
+ 1)
99
and you want to find h
0
(x). It would be ridiculous
to multiply it out—you’d have to multiply x
2
+ 1 by itself 99 times and it
would take days. It would also be crazy to use the product rule, since you’d
need to use it too many times.
Instead, let’s view h as the composition of two functions f and g, where
g(x) = x
2
+ 1 and f (x) = x
99
. Indeed, if you take your x and hit it with g,
you end up with x
2
+ 1. If you now hit that with f, you get (x
2
+ 1)
99
, which
is just h(x). So we have written h(x) as f(g(x)). (Check out Section 1.3 in
Chapter 1 for more on how composition of functions works.) Now we can
apply the chain rule:
Chain rule (version 1): if h(x) = f (g(x)), then h
0
(x) = f
0
(g(x))g
0
(x).
The formula looks a little tricky. Let’s decompose it. The second factor is
easy: it’s just the derivative of g. How about the first factor? Well, you have
to differentiate f, then evaluate the result at g(x) instead of x.
In our example, we have f (x) = x
99
, so f
0
(x) = 99x
98
. We also have
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
g(x) = x
2
+ 1, so g
0
(x) = 2x. There’s our second factor: just 2x. How about
the first one? Well, we take f
0
(x), but instead of x, we put in x
2
+ 1 (since
that’s what g(x) is). That is, f
0
(g(x)) = f
0
(x
2
+ 1) = 99(x
2
+ 1)
98
. Now we
multiply our two factors together to get
h
0
(x) = f
0
(g(x))g
0
(x) = 99(x
2
+ 1)
98
(2x) = 198x(x
2
+ 1)
98
.
This might seem a little tortuous, to say the least. Here’s another way to
solve the same problem.
We start with y = (x
2
+ 1)
99
and we want to find dy/dx. The (x
2
+ 1)
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
term makes life difficult, so we’ll just call it u. This means that y = u
99
where
u = x
2
+ 1. Now we can invoke the other version of the chain rule:
Chain rule (version 2): if y is a function of u,
and u is a function of x, then
dy
dx
=
dy
du
du
dx
.
So in our case, we have
y = u
99
u = x
2
+ 1
dy
du
= 99u
98
du
dx
= 2x.
Using the chain rule formula in the box above, we see that
dy
dx
=
dy
du
du
dx
= 99u
98
× 2x = 198xu
98
.
Now you just need to tidy it up by replacing u by x
2
+ 1 to see that we have
dy/dx = 198x(x
2
+ 1)
98
, as we found above.

108 • How to Solve Differentiation Problems
Here’s another straightforward example. If y =
√
x
3
− 7x, what is dy/dx?
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
Start by setting u = x
3
− 7x, so that y =
√
u. Our table looks like this:
y =
√
u u = x
3
− 7x
dy
du
=
1
2
√
u
du
dx
= 3x
2
− 7.
So by the chain rule, we have
dy
dx
=
dy
du
du
dx
=
1
2
√
u
× (3x
2
− 7) =
3x
2
− 7
2
√
u
.
Now we just have to get rid of the u in the denominator; since u = x
3
− 7x,
we see that
dy
dx
=
3x
2
− 7
2
√
x
3
− 7x
.
Not so bad when you get the hang of it.
Two quick comments on the chain rule. First, why is it called the chain
rule, anyway? Well, you start with x and it gives you u; then you take that
u and get y. So there’s a sort of chain from x to y through the extra variable
u. Second, you might think that the chain rule is obvious. After all, in the
formula in the box on the previous page, can’t you just cancel out the factor
of du? The answer is no—remember, expressions like dy/du and du/dx aren’t
actually fractions, they are limits of fractions (see Section 5.2.7 in the previous
chapter for more on this). The nice thing is that they often behave as if they
were fractions—they certainly do in this case.
The chain rule can actually be invoked multiple times all at once. For
example, let
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
y = ((x
3
− 10x)
9
+ 22)
8
.
What is dy/dx? Simply let u = x
3
− 10x, and v = u
9
+ 22, so that y = v
8
.
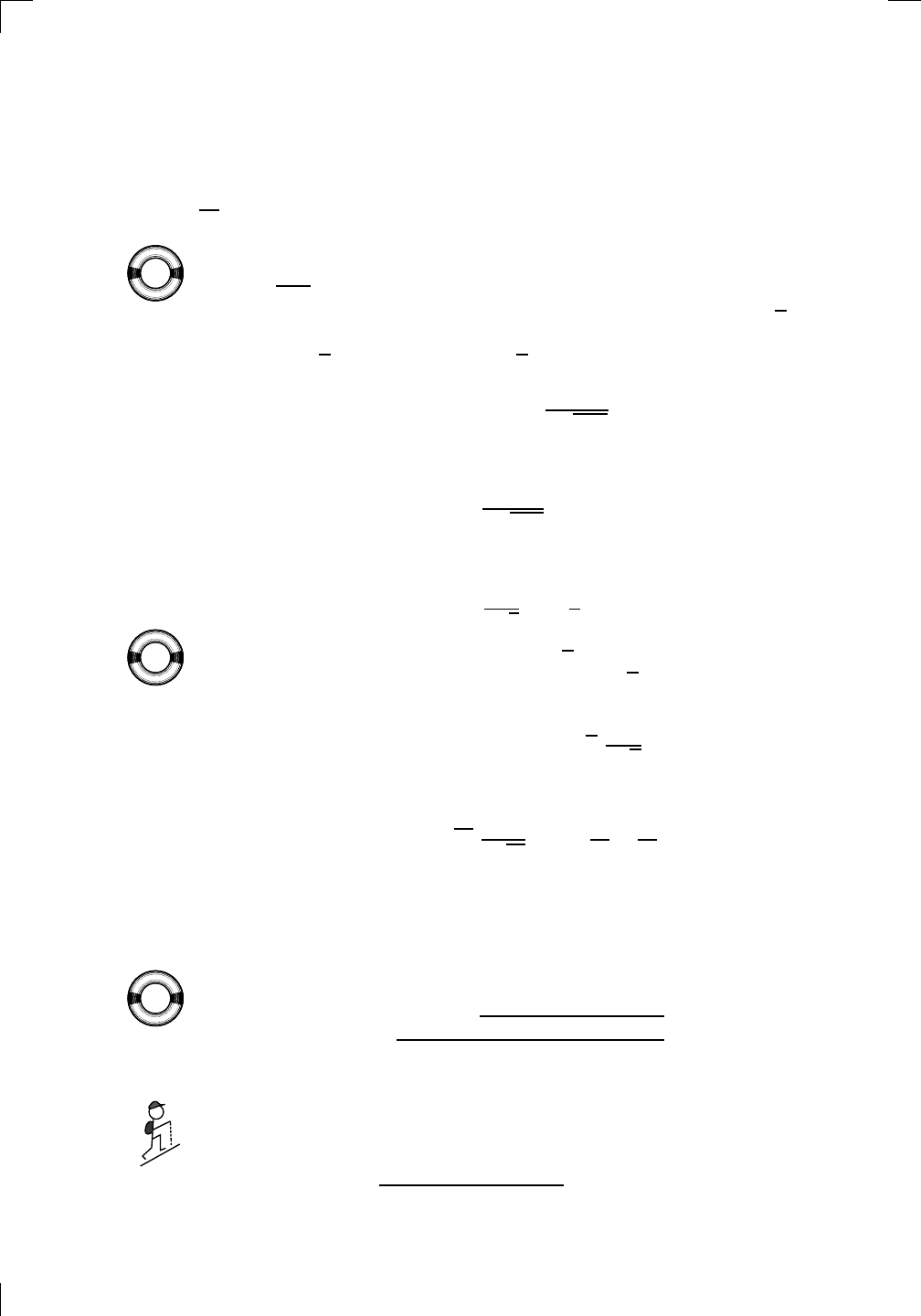
Then use a longer form of the chain rule:
dy
dx
=
dy
dv
dv
du
du
dx
.
You can’t get this wrong if you think about it: y is a function of v, which is
a function of u, which is a function of x. So there’s only one way the formula
could possibly look! Anyway, we have
y = v
8
v = u
9
+ 22 u = x
3
− 10x
dy
dv
= 8v
7
dv
du
= 9u
8
du
dx
= 3x
2
− 10.
Plugging everything in, we have
dy
dx
=
dy
dv
dv
du
du
dx
= (8v
7
)(9u
8
)(3x
2
− 10).
We’re close, but we need to get rid of the u and v terms. First, replace v by
u
9
+ 22:
dy
dx
= (8v
7
)(9u
8
)(3x
2
− 10) = (8(u
9
+ 22)
7
)(9u
8
)(3x
2
− 10).
Section 6.2.6: A nasty example • 109
Now replace u by x
3
− 10x and group the factors of 8 and 9 together to get
the actual answer:
dy
dx
= (8(u
9
+22)
7
)(9u
8
)(3x
2
−10) = 72((x
3
−10x)
9
+22)
7
(x
3
−10x)
8
(3x
2
−10).
We’ve mostly used the second version of the chain rule above, but there are
times when the first version comes in useful. For example, if you know that
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
h(x) =
p
g(x) for some functions g and h, and all you know about g is that
g(5) = 4 and g
0
(5) = 7, then you can still find h
0
(5). Just set f(x) =
√
x so
that h(x) = f (g(x)), then use the formula h
0
(x) = f
0
(g(x))g
0
(x) from above.
Since f(x) =
√
x, we have f
0
(x) = 1/2
√
x; so
h
0
(x) = f
0
(g(x))g
0
(x) =
1
2
p
g(x)
g
0
(x).
Now substitute x = 5 to get
h
0
(5) =
1
2
p
g(5)
g
0
(5).
Since g(5) = 4 and g
0
(5) = 7, we have
h
0
(5) =
1
2
√
4
(7) =
7
4
.
One more example: suppose that j(x) = g(
√
x), where g is as above. What
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
is j
0
(25)? Now we have j(x) = g(f(x)); here f(x) =
√
x as before. This time,
it works out that
j
0
(x) = g
0
(f(x))f
0
(x) = g
0
(
√
x)
1
2
√
x
.
So if x = 25, we have
j
0
(25) = g
0
(
√
25)
1
2
√
25
= g
0
(5)
1
10
=
7
10
since g
0
(5) = 7. Compare these two examples: the order of composition makes
a big difference!
6.2.6 A nasty example
Let’s return to our function f from above:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
f(x) =
3x
7
+ x
4
√
2x
5
+ 15x
4/3
− 23x + 9
6x
2
− 4
.
To find f
0
(x), we have to synthesize f from easier functions using the rules
from the previous sections. It’s not a bad idea to do this using the function
notation (version 1 of all the rules above). Try this now!
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
Meanwhile, I’m going to use version 2 of all the rules. We’ll set y = f(x)
and try to find dy/dx. The first thing to notice is that y is the quotient of two
things: u = 3x
7
+ x
4
√
2x
5
+ 15x
4/3
− 23x + 9 and v = 6x
2
− 4. We’re going

110 • How to Solve Differentiation Problems
to use the quotient rule to deal with the fraction, so we’ll need du/dx and
dv/dx. The second of these is easy: it’s just 12x. The first is a bit harder.
Let’s summarize what we know so far:
u = 3x
7
+ x
4
p
2x
5
+ 12x
4/3
− 23x + 9 v = 6x
2
− 4
du
dx
=???
dv
dx
= 12x.
If we just knew du/dx, we could use the quotient rule and we’d be done. So
let’s find du/dx.
First, note that u is the sum of q = 3x
7
and the nasty quantity r defined
by r = x
4
√
2x
5
+ 15x
4/3
− 23x + 9. We need the derivatives of both pieces.
The derivative of q is easy: it’s just 21x
6
. Now, r is the product of w = x
4
and z =
√
2x
5
+ 15x
4/3
− 23x + 9, so we’ll have to use the product rule to
find dr/dx. We’ll need to note the following:
w = x
4
z =
p
2x
5
+ 15x
4/3
− 23x + 9
dw
dx
= 4x
3
dz
dx
= ???
Darn, we don’t know what dz/dx is. We’re going to need to find that. Here
we are taking the square root of a big expression, so let’s call it t. Specifically,
if t = 2x
5
+ 15x
4/3
−23x + 9, then z =
√
t. Now we can actually differentiate
everything! Let’s set up one last table:
t = 2x
5
+ 15x
4/3
− 23x + 9 z =
√
t
dt
dx
= 10x
4
+ 20x
1/3
− 23
dz
dt
=
1
2
√
t
.
By the chain rule (changing the variables to the letters we need),
dz
dx
=
dz
dt
dt
dx
=
1
2
√
t
10x
4
+ 20x
1/3
− 23
.
Replacing t by its definition, 2x
5
+ 15x
4/3
− 23x + 9, we see that
dz
dx
=
10x
4
+ 20x
1/3
− 23
2
√
2x
5
+ 15x
4/3
− 23x + 9
.
Great—we finally know dz/dx. Now we can fill in the question marks from
above:
w = x
4
z =
p
2x
5
+ 15x
4/3
− 23x + 9
dw
dx
= 4x
3
dz
dx
=
10x
4
+ 20x
1/3
− 23
2
√
2x
5
+ 15x
4/3
− 23x + 9
.
Now look back above—we were trying to find dr/dx, where r = wz. Let’s use
the product rule:
dr
dx
= z
dw
dx
+ w
dz
dx
.
Again, notice that you have to be flexible with the variables—they’re not
always u and v! Anyway, if you substitute from the table above, you find that
dr
dx
=
p
2x
5
+ 15x
4/3
− 23x + 9
(4x
3
) + (x
4
)
10x
4
+ 20x
1/3
− 23
2
√
2x
5
+ 15x
4/3
− 23x + 9
.
Section 6.2.7: Justification of the product rule and the chain rule • 111
Taking a common denominator and simplifying reduces this (check it!) to
dr
dx
=
26x
8
+ 140x
13/3
− 207x
4
+ 72x
3
2
√
2x
5
+ 15x
4/3
− 23x + 9
.
Now go back to u. We saw that u = q + r, where we have q = 3x
7
and
r = x
4
√
2x
5
+ 15x
4/3
− 23x + 9. We know that dq/dx = 21x
6
, and we just
worked out the messy formula for dr/dx, so we just add them together to get
du
dx
= 21x
6
+
26x
8
+ 140x
13/3
− 207x
4
+ 72x
3
2
√
2x
5
+ 15x
4/3
− 23x + 9
.
Finally, we can come back to our original quotient rule computation from the
top of the previous page, and fill in du/dx:
u = 3x
7
+ x
4
p
2x
5
+ 15x
4/3
− 23x + 9 v = 6x
2
− 4
du
dx
= 21x
6
+
26x
8
+ 140x
13/3
− 207x
4
+ 72x
3
2
√
2x
5
+ 15x
4/3
− 23x + 9
dv
dx
= 12x.
Since y = u/v, we just use the standard quotient rule
dy
dx
=
v
du
dx
− u
dv
dx
v
2
to see (after splitting up and canceling) that
dy
dx
=
21x
6
+
26x
8
+ 140x
13/3
− 207x
4
+ 72x
3
2
√
2x
5
+ 15x
4/3
− 23x + 9
6x
2
− 4
−
3x
7
+ x
4
√
2x
5
+ 15x
4/3
− 23x + 9
(12x)
(6x
2
− 4)
2
.
We’re finally done! It’s certainly not pretty, but it’s certainly effective.
6.2.7 Justification of the product rule and the chain rule
You can find formal proofs of the product rule and chain rule in Sections A.6.3
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
and A.6.5 of Appendix A, but it’s not a bad idea to get an intuitive idea for
why these rules work. So let’s take a quick look.
In the case of the product rule, we’ll use version 2 of the rule from Sec-
tion 6.2.3 above. We start off with two quantities, u and v, which both depend
on some variable x. We want to see how the product uv changes when we
change x by a tiny amount ∆x. Well, u will change to u + ∆u, and v will
change to v + ∆v, so the product changes to (u + ∆u)(v + ∆v). We can
visualize this by thinking of a rectangle with side lengths u and v units. The
rectangle changes shape a little bit so that its new dimensions are u + ∆u and
v + ∆v units, like this:
112 • How to Solve Differentiation Problems
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f(x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
The products uv and (u+ ∆u)(v +∆v) are just the areas of the two rectangles
in square units, respectively. So how much does the area change? Let’s see
by superimposing the two rectangles:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f (x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
The change in areas is precisely the area of the shaded L-shaped region. This
region is made up of two thin rectangles (of areas v∆u and u∆v square units)
and one little one (of area (∆u)(∆v) square units). Since the change of areas
is ∆(uv) square units, we have shown that
∆(uv) = v∆u + u∆v + (∆u)(∆v).
When the quantities ∆u and ∆v are very small, the little area is very very
small indeed, so we can basically ignore it. Here’s what we’re saying:
∆(uv)
∼
=
v∆u + u∆v.
If you divide by ∆x and take limits, the approximation becomes perfect and
we get the product rule
d
dx
(uv) = v
du
dx
+ u
dv
dx
.
This is actually pretty close to the real proof!
Before we move onto the chain rule, let’s prove the product rule for three
functions, which is (as we saw above) given by
d
dx
(uvw) =
du
dx
vw + u
dv
dx
w + uv
dw
dx
.
The trick is to let z = vw, so that uvw is just uz. We can use the product
rule on z = vw first:
dz
dx
= w
dv
dx
+ v
dw
dx
.

Section 6.2.7: Justification of the product rule and the chain rule • 113
Now use the product rule on uz to get
d
dx
(uvw) =
d
dz
(uz) = z
du
dx
+ u
dz
dx
.
All that’s left is to replace z by vw and dz/dx by the above expression to see
that
d
dx
(uvw) = z
du
dx
+ u
dz
dx
= vw
du
dx
+ u
w
dv
dx
+ v
dw
dx
.
If you expand this, you get the desired formula.
Finally, let’s think about the chain rule for a little bit. Suppose y = f (u)
and u = g(x). This means that u is a function of x, and y is a function of u.
If we change x by a little bit, as a result u will also change by a little bit. As
a result of that, y will change too. By how much will y change?
Well, let’s start off by concentrating on u and seeing how it reacts to a small
change in x. Remember that u = g(x); so as we discussed in Section 5.2.7
in the previous chapter, the change in u will be approximately g
0
(x) times
the change in x. You can think of g
0
(x) as a sort of stretching factor. (For
example, if you stand in front of one of those amusement park mirrors that
make you look twice as tall and skinny as you are, then stand on your toes,
your reflection will rise by twice as much as you do.) Here’s an equation that
describes this:
∆u
∼
=
g
0
(x) ∆x.
Now we can repeat the exercise with y in terms of u. Since y = f(u), a change
in u will produce approximately f
0
(u) times as much change in y:
∆y
∼
=
f
0
(u) ∆u.
Putting these two equations together, we get
∆y
∼
=
f
0
(u)g
0
(x) ∆x.
So the change in x is first stretched by a factor of g
0
(x), then again by a factor
of f
0
(u). The overall effect is to stretch by the product of the two stretching
factors f
0
(u) and g
0
(x). (After all, if you stretch a piece of chewing gum by
a factor of 2, then stretch that by a factor of 3, this would be the same
as stretching the original piece of gum by a factor of 6.) This last equation
suggests that
dy
dx
= lim
∆x→0
∆y
∆x
= f
0
(u)g
0
(x).
From here, you can get to either of the two versions of the chain rule without
too much difficulty. To get version 1, remember that u = g(x) and y = f(u),
so that y = f (g(x)); then let y = h(x) and rewrite the above equation as
h
0
(x) = f
0
(u)g
0
(x) = f
0
(g(x))g
0
(x).
To get version 2, just interpret f
0
(u) as dy/du and also g
0
(x) as du/dx, so
that the above equation for dy/dx says that
dy
dx
=
dy
du
du
dx
.
The above explanation isn’t a formal proof, but it’s pretty close.

114 • How to Solve Differentiation Problems
6.3 Finding the Equation of a Tangent Line
What’s the use of finding derivatives, anyway? Well, one benefit is that you
can use derivatives to find the equation of a tangent line to a given curve.
Suppose you have a curve y = f (x) and a particular point (x, f(x)) on the
curve. Then the tangent line through that point has slope f
0
(x) and passes
through the point (x, f(x)). Now you can just use the point-slope form to
find the equation of the tangent line. In gory detail:
1. find the slope, by finding the derivative and plugging in the given value
of x;
2. find a point on the line, by substituting the value of x into the
function itself to get the y-coordinate. Put the coordinates together and
call the resulting point (x
0
, y
0
). Finally,
3. use the point-slope form y − y
0
= m(x − x
0
) to find the equation.
Here’s an example. Let y = (x
3
− 7)
50
. What is the equation of the tangent
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
line to the graph of this function at x = 2? First we need the derivative. We’ll
have to use the chain rule, as follows: let u = x
3
− 7, so y = u
50
. Then we
have dy/du = 50u
49
and du/dx = 3x
2
. By the chain rule,
dy
dx
=
dy
du
du
dx
= 50u
49
× 3x
2
= 150x
2
(x
3
− 7)
49
.
(Remember, we have to replace u by x
3
−7 in order to get everything in terms
of x.) Now we need to plug in x = 2; for this value of x, we have
dy
dx
= 150(2)
2
(2
3
− 7)
49
= 150 × 4 × 1
49
= 600.
Great—we’ve found the slope of the tangent line we’re looking for. Now we
need to find a point it goes through: just put x = 2 and see what y is. In
fact, y = (2
3
− 7)
50
= 1
50
= 1. So the tangent line passes through (2, 1).
Using the point-slope form, we see that the equation of the tangent line is
(y − 1) = 600(x − 2), which you can rewrite as y = 600x − 1199 if you like.
And that’s all there is to finding tangent lines!
6.4 Velocity and Acceleration
Another application of finding derivatives is to compute velocities and acceler-
ations of moving objects. In Section 5.2.2 of the previous chapter, we imagined
that an object moves along a number line. We saw that if its position at time
t is x, then its velocity
∗
at time t is given by
velocity = v =
dx
dt
.
Now, just as the velocity is the instantaneous rate at which the position
changes, the acceleration of the object is the instantaneous rate at which the
∗
From now on, we’ll drop the word “instantaneous”; the term “velocity” will always
refer to instantaneous velocity unless we actually say “average velocity.”

Section 6.4.1: Constant negative acceleration • 115
velocity changes. That is, the acceleration is the derivative of the velocity
with respect to time t. Since the velocity is the derivative of the position, we
see that the acceleration is actually the second derivative of the position. So
we have
acceleration = a =
dv
dt
=
d
2
x
dt
2
.
For example, let’s say that we know that the position of an object at time
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
t is given by x = 3t
3
− 6t
2
+ 4t − 2, where x is in feet and t is in seconds.
What are the object’s velocity and acceleration at time t = 3? Well, we get
the velocity by differentiating the position with respect to time, just like this:
v = dx/dt = 9t
2
− 12t + 4. Now we differentiate this new expression with
respect to time to get the acceleration: a = dv/dt = 18t − 12. Now plug in
t = 3 to get v = 9(3)
2
−12(3)+4 = 49 ft/sec, and a = 18(3)−12 = 42 ft/sec
2
.
Why is the acceleration given in feet per second squared? Well, when you
ask what the acceleration of an object is, you are really asking how fast the
object’s speed is changing. If the speed changes from 15 ft/sec to 25 ft/sec
over a time period of 2 seconds, then it has (on average) changed by 5 ft/sec
per second. So acceleration should be written in feet per second per second,
or just feet per second squared. In general, you always have to square the
time unit when you are dealing with acceleration.
6.4.1 Constant negative acceleration
Suppose you throw a ball directly up in the air. It goes up and comes back
down (unless it hits something or someone else catches it!). This is because
the Earth’s gravitational pull exerts a force on the ball, pulling it toward the
Earth. Newton—one of the pioneers of calculus—realized that the effect of
the force is that the ball moves downward with constant acceleration. (We’ll
assume that there’s no air resistance.)
Since the ball is going up and down, we’d better reorient our number line
so that it points up and down. Let’s set the 0 point as being on the ground,
and we’ll make upward positive. Since the acceleration is downward, it must
be a negative quantity, and since it’s constant, we can just call it −g. On
Earth, g is about 9.8 meters per second squared, but it’s a lot less on the
moon. Anyway, if we’re going to understand how this ball moves, we need to
know its position and its velocity at time t.
Let’s start off with velocity. We know that a = dv/dt. In the example
in the previous section, we knew what v was, so we differentiated it to find
a. Unfortunately, this time we know what a is (it’s the constant −g) and
we need to find v; so we’re all topsy-turvy here. The same thing happens
for x, once we know v. In both cases, we need to reverse the process of
differentiation. Unfortunately, we’re not ready for this yet—that’s part of
what integration is all about. So I’m just going to tell you the answer, then
verify it by differentiating:
An object thrown at time t = 0 from initial height h with
initial velocity u satisfies the equations
a = −g, v = −gt + u, and x = −
1
2
gt
2
+ ut + h.
