Banner A. The Calculus Lifesaver: All the Tools You Need to Excel at Calculus
Подождите немного. Документ загружается.

76 • Continuity and Differentiability
x = 0. So we have to understand what it means to be continuous at a point,
and then we’ll worry about continuity over larger regions like intervals.
5.1.1 Continuity at a point
Let’s start with a function f and a point a on the x-axis which is in the domain
of f. When we draw the graph of y = f(x), we don’t want to lift up the pen
as we pass through the point (a, f(a)) on the graph. It doesn’t matter if we
have to lift up our pen elsewhere, as long as we don’t lift it up near (a, f(a)).
This means that we want a stream of points (x, f(x)) which get closer and
closer—arbitrarily close, in fact—to the point (a, f(a)). In other words, as
x → a, we need f (x) → f(a). Yes, ladies and gentlemen, we’re dealing with
limits here. We can now give a proper definition:
A function f is continuous at x = a if lim
x→a
f(x) = f (a).
Of course, for this last equation to make sense at all, both sides must be
defined. If the limit doesn’t exist, then f isn’t continuous at x = a, whereas
if f(a) doesn’t exist, then you’re totally screwed: there isn’t even a point
(a, f(a)) to go through! So we can be a little more precise about the definition
and explicitly require three things to be true:
1. The two-sided limit lim
x→a
f(x) exists (and is finite).
2. The function is defined at x = a; that is, f(a) exists (and is finite).
3. The two above quantities are equal: that is,
lim
x→a
f(x) = f(a).
Let’s see what happens if any of these properties fail. Consider the following
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
graphs:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−2π
−
3π
2
−π
−
π
2
3π
5π
2
2π
2π
3π
2
π
π
2
y = sin(x)
y = cos(x)
−
π
2
π
2
y = tan(x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(x)
−2π
−3π
−
5π
2
−
3π
2
−π
−
π
2
π
2
3π
3π
5π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f (x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a a a a
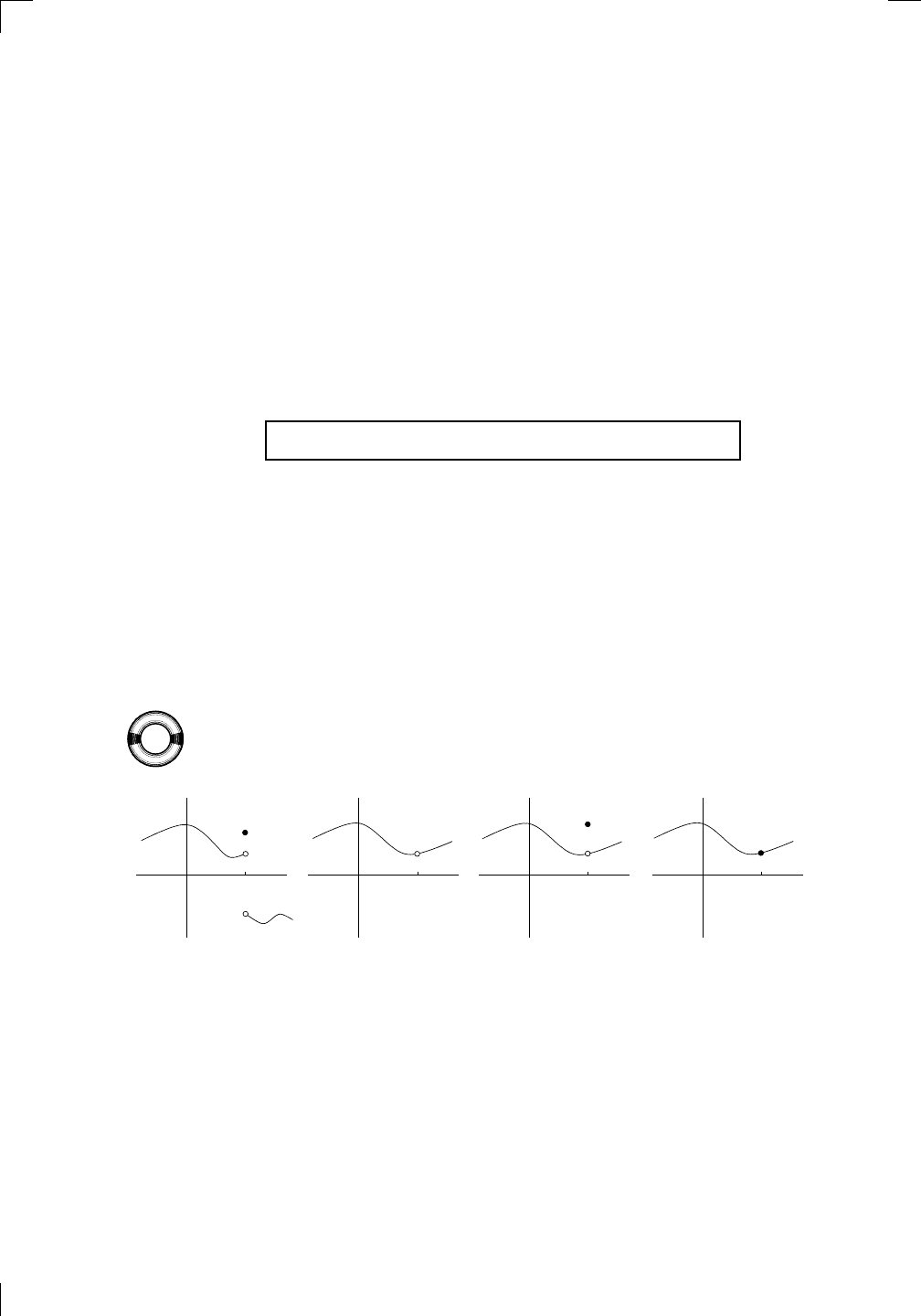
In diagram #1, the left- and right-hand limits aren’t the same at x = a, so
the two-sided limit doesn’t exist there; therefore the function isn’t continuous
at x = a. In diagram #2, the left- and right-hand limits exist and are finite
and equal to each other, so the two-sided limit exists; however the function
isn’t even defined at x = a, so it isn’t continuous there. In diagram #3, the
two-sided limit again exists, and the function is defined at x = a, but the limit
isn’t the same as the function value; once again, the function isn’t continuous
at x = a. On the other hand, the function in diagram #4 is indeed continuous
at x = a, since the two-sided limit at x = a exists, f (a) exists, and the limit is
the same as the value of the function. By the way, we say that the functions
in the first three diagrams have a discontinuity at x = a.

Section 5.1.2: Continuity on an interval • 77
5.1.2 Continuity on an interval
We now know what it means for a function to be continuous at a single point.
Let’s extend this definition and say that a function f is continuous on the
interval (a, b) if it is continuous at every point in the interval. Notice that
f doesn’t actually have to be continuous at the endpoints x = a or x = b.
For example, if f(x) = 1/x, then f is continuous on the interval (0, ∞) even
though f(0) isn’t defined. This function is also continuous on (−∞, 0), but
not on (−2, 3), since 0 lies within that interval, and f isn’t continuous there.
How about an interval like [a, b]? We have to be a little more flexible. For
example, below is the graph of a function with domain [a, b]; we’d like to say
that it’s continuous on [a, b]:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
The problem is that the two-sided limits at the endpoints x = a and x = b
don’t exist: we only have a right-hand limit at x = a and a left-hand limit at
x = b. That’s OK; we just modify our definition a bit by using the appropriate
one-sided limits at the endpoints. So we say that a function f is continuous
on [a, b] if
1. the function f is continuous at every point in (a, b);
2. the function f is right-continuous at x = a. That is, lim
x →a
+
f(x) exists
(and is finite), f(a) exists, and these two quantities are equal; and
3. the function f is left-continuous at x = b. That is, lim
x →b
−
f(x) exists (and
is finite), f(b) exists, and these two quantities are equal.
Finally, we just say that a function is continuous if it is continuous at all
the points in its domain, with the understanding that if its domain includes
an interval with a left and/or right endpoint, then we only need one-sided
continuity there.
5.1.3 Examples of continuous functions
Many common functions are continuous. For example, every polynomial is
continuous. This seems a little hard to prove, since there are so many different
polynomials, but actually it’s not so bad. First, let’s prove that the constant
function f, defined by f(x) = 1 for all x, is continuous at any point a. Well,
we need to show that
lim
x→a
f(x) = f(a).
Since f(x) = 1 for any x, and f(a) = 1, then this means that we need to show
that
lim
x→a
1 = 1.

78 • Continuity and Differentiability
Of course, this is obviously true, since nothing depends on x or a! Now, let’s
set g(x) = x. Is g continuous? Well, now we need
lim
x→a
g(x) = g(a).
Since g(x) = x and g(a) = a, this reduces to showing that
lim
x→a
x = a.
This is also obviously true: as x → a, well, x → a! Now we just need to observe
that a constant multiple of a continuous function is continuous; also, if you
add, subtract, multiply or take the composition of two continuous functions,
you get another continuous function (see Section A.4.1 of Appendix A for
more info). The same is almost true if you divide one continuous function
by another: the quotient function is continuous everywhere except where the
denominator is 0. For example, 1/x is continuous except at x = 0, since we’ve
seen that both the numerator and denominator are continuous functions of x.
Anyway, back to polynomials. Because g(x) = x is continuous in x, we
can multiply g by itself to see that x
2
is also continuous in x. You can keep
multiplying by x as often as you like to prove the continuity of any power of
x (as a function of x). Then you can multiply by constant coefficients and
add different powers together to get any polynomial—and everything’s still
continuous!
It turns out that all exponentials and logarithms are continuous, as are all
the trig functions (except where they have vertical asymptotes). We’ll just
take that for granted for the moment and return to this point in Section 5.2.11
below. Meanwhile, I want to look at a more exotic function. Consider the
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
function f defined by f(x) = x sin(1/x). We looked at the graph of this (at
least when x > 0) in Section 3.6 of Chapter 3. In fact, it’s really easy to extend
the graph to x < 0, because f is an even function. Why? Remembering that
sin(x) is an odd function of x, we have
f(−x) = (−x) sin
1
−x
= (−x)
−sin
1
x
= x sin
1
x
= f(x).
So f is indeed even, and we can get the graph of all of f by reflecting the pre-
vious graph using the y-axis as our mirror (the graph only shows the domain
−0.3 < x < 0.3):
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y = tan(x)
−2π
−3π
−
5π
2
−
3π
2
−π
−
π
2
π
2
3π
3π
5π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f (x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f(x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x

Section 5.1.3: Examples of continuous functions • 79
Now let’s consider the continuity of the function. As a function of x, we
know that 1/x is continuous away from x = 0; now compose this with the
sine function, which is also continuous, and you can see that sin(1/x) is also
continuous away from x = 0. Now you just have to multiply sin(1/x) by x
(which is obviously a continuous function of x!) to see that f is continuous
everywhere except at x = 0.
Now, what happens at x = 0? Clearly f is not continuous at x = 0, since
it’s not even defined there (there’s a hole in the graph). Let’s plug up this
hole by defining a function g as follows:
g(x) =
x sin
1
x
if x 6= 0,
0 if x = 0.
So g(x) = f (x) everywhere except at x = 0, where g equals 0 but f is un-
defined. As a result, g is automatically continuous everywhere f is—namely,
everywhere except x = 0—but now we need to see what happens at x = 0.
We have a hope because g(0) is defined. Also, we used the sandwich principle
in Section 3.6 of Chapter 3 to show that
lim
x→0
+
g(x) = lim
x→0
+
x sin
1
x
= 0.
By symmetry (or the sandwich principle, again), we can see that the left-hand
limit is also equal to 0. So in fact the two-sided limit is 0 as well:
lim
x→0
g(x) = lim
x→0
x sin
1
x
= 0.
So we have shown that
lim
x→0
g(x) = g(0)
since both sides exist and are equal to 0. This means that g is actually
continuous at x = 0, even though it was cobbled together in piecewise fashion.
We’re almost ready to look at two nice facts involving continuity; first I
want to return to a point I made at the beginning of Chapter 4. The first
example we looked at was
lim
x→−1
x
2
− 3x + 2
x − 2
,
which we solved by just substituting x = −1 to get the answer −2. Why is
this justified? The argument seems to contradict the idea that the value of
the above limit has nothing to do with what happens at x = −1, only what
happens near x = −1. This is where continuity comes in: it connects the
“near” with the “at.” Specifically, if we let f(x) = (x
2
− 3x + 2)/(x − 2),
then since the numerator and denominator are polynomials, f is continuous
everywhere except where the denominator is 0. That is, f is continuous
everywhere except at x = 2. So f is continuous at x = −1, which means that
lim
x→−1
f(x) = f (−1).
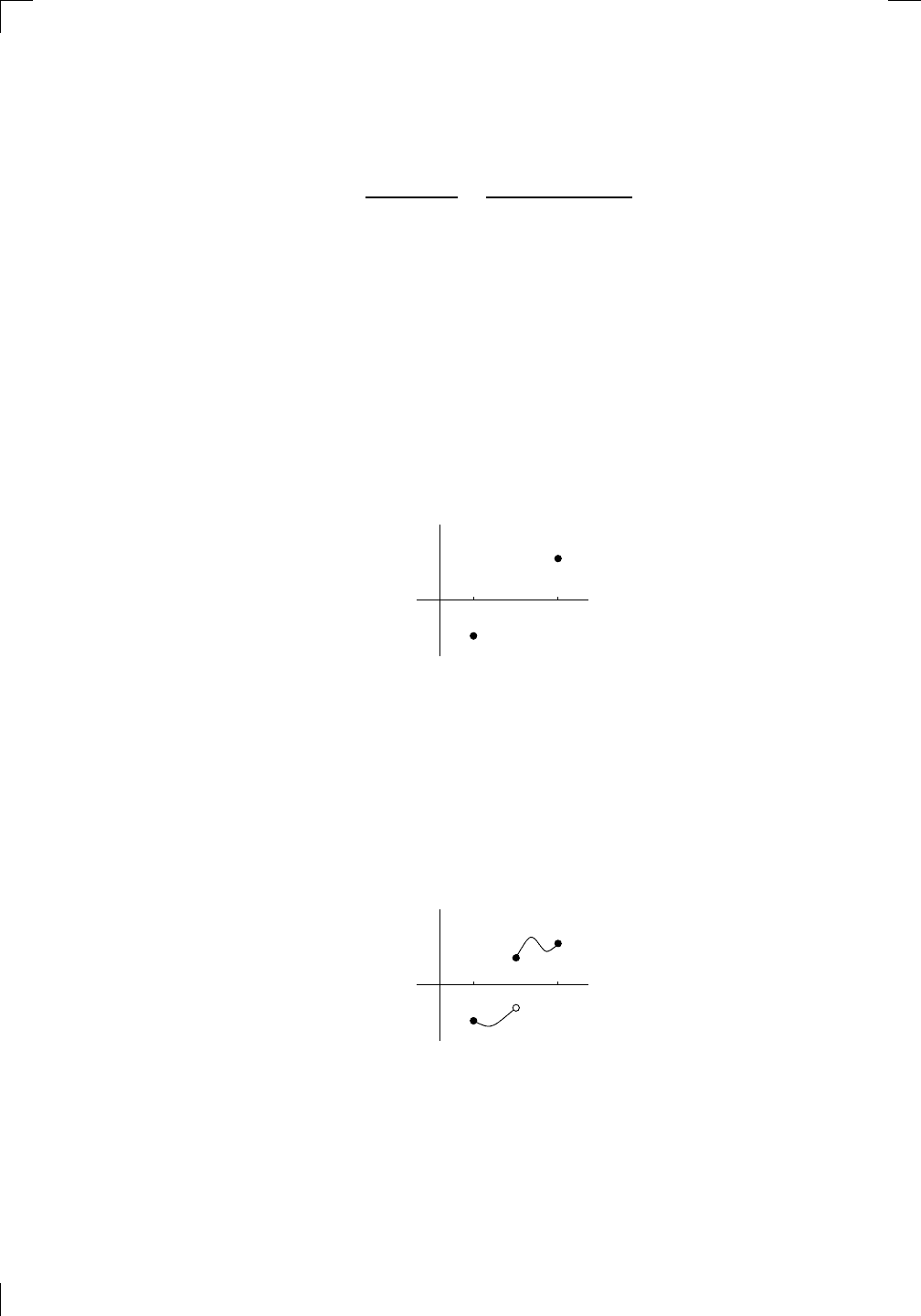
80 • Continuity and Differentiability
Replacing f by its definition, we have
lim
x→−1
x
2
− 3x + 2
x − 2
=
(−1)
2
− 3(−1) + 2
(−1) − 2
= −2.
That is the complete solution. In practice, few mathematicians would bother
spelling it out in such gory detail, but it’s worth understanding what you’re
doing whenever possible!
5.1.4 The Intermediate Value Theorem
Knowing that a function is continuous brings some benefits. We’re going to
look at two such benefits. The first is called the Intermediate Value Theorem,
or IVT for short. Here’s the idea: let’s suppose that a function f is continuous
on a closed interval [a, b]. Also suppose that f(a) < 0 and f(b) > 0. So in the
graph of y = f(x), we know that the point (a, f(a)) lies below the x-axis and
that the point (b, f (b)) lies above the x-axis, like this:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
Now, if you have to connect those two points with a curve (which of course
has to obey the vertical line test), and you’re not allowed to lift your pen up,
it’s intuitively obvious that your pen will have to cross the x-axis somewhere
between a and b, at least once. It could be close to a or close to b, or somewhere
in the middle; you might cross back and forth many times; but the critical
thing is that you have to cross at least once. That is, there is an x-intercept
somewhere between a and b. It’s crucial that the function f is continuous at
every point in [a, b]; look what can happen if f is discontinuous at even one
point:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
The discontinuity allows this function to jump over the x-axis without passing
through it. So, we need continuity on the whole region [a, b]. All this is also
true if we start above the axis and end below it; that is, if f(a) > 0 and
f(b) < 0, we must have an x-intercept somewhere in [a, b] if f is continuous
on all of [a, b]. Since an x-intercept at c means that f(c) = 0, we can state
the Intermediate Value Theorem as follows:

Section 5.1.4: The Intermediate Value Theorem • 81
Intermediate Value Theorem: if f is continuous on [a, b], and f(a) < 0
and f(b) > 0, then there is at least one number c in the interval (a, b)
such that f(c) = 0. The same is true if instead f(a) > 0 and f (b) < 0.
There’s a proof of this theorem in Section A.4.2 of Appendix A. For now,
let’s look at a few examples of how to apply this theorem. First, suppose
you want to show that the polynomial p(x) = −x
5
+ x
4
+ 3x + 1 has an
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
x-intercept between x = 1 and x = 2. All you have to do is notice that
p is continuous everywhere (including [1, 2]) because it’s a polynomial; also,
calculate p(1) = 4 > 0 and p(2) = −9 < 0. Since p(1) and p(2) have opposite
signs and p is continuous on [1, 2], we know that there is at least one number
c in the interval (1, 2) such that p(c) = 0. This number c is an x-intercept of
the polynomial p.
Here’s a slightly harder example. How would you show that the equation
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
x = cos(x) has a solution? You don’t have to find the solution, only to
show that there is one. You could start by drawing the graphs of y = x and
y = cos(x) on the same axes. If you do, you’ll find that the intersection of the
graphs has x-coordinate somewhere around π/4. This graphical argument,
while compelling, doesn’t cut it so far as a mathematical proof is concerned.
How can we do better?
The first step is to use a little trick: put everything onto the left-hand
side. So, instead of solving x = cos(x), we try to solve x − cos(x) = 0. Now
we must take the initiative and set f(x) = x −cos(x). We’ll be all done if we
can show that there is a number c such that f(c) = 0. Let’s check that this
makes sense: if f(c) = 0, then c −cos(c) = 0, so c = cos(c) and we have found
a solution to the equation x = cos(x), namely x = c.
Now it’s time to use the Intermediate Value Theorem. We need to find
two numbers a and b such that one of f(a) and f(b) is negative and the other
one is positive. Since we think (from the graph) that the answer is around
π/4, we’ll be conservative and take a = 0 and b = π/2. Let’s check the values
of f(0) and f(π/2). First, f(0) = 0 −cos(0) = 0 −1 = −1, which is negative,
and second, f(π/2) = π/2 − cos(π/2) = π/2 − 0 = π/2, which is positive.
Since f is continuous (it is the difference of two continuous functions), we
can conclude by the Intermediate Value Theorem that f(c) = 0 for some c
in the interval (0, π/2), and we have shown that x = cos(x) has a solution.
We don’t know where the solution is, nor how many solutions there are—only
that there is at least one solution in the interval (0, π/2). (Note that the
solution is not really at π/4! It’s not possible to find a nice expression for the
answer, actually.)
Here’s a small variation. So far, we have required that f(a) < 0 and
f(b) > 0 (or the other way around), then concluded that there’s a number
c in (a, b) such that f(c) = 0. Instead, we can replace 0 by any number M
and the result is still true. So, suppose f is continuous on [a, b]; if f(a) < M
and f(b) > M (or the other way around), then there is some c in (a, b) such
that f(c) = M . For example, if f(x) = 3
x
+ x
2
, then does the equation
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
f(x) = 5 have a solution? Certainly f is continuous; also we can guess to
plug in 0 and 2, which leads to f(0) = 1 and f(2) = 13. Since the numbers 1
and 13 surround the target number 5 (one is smaller and the other is bigger),
the Intermediate Value Theorem tells us that f (c) = 5 for some c in (0, 2).

82 • Continuity and Differentiability
That is, f(x) = 5 does have a solution. Now, try to repeat the problem by
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
starting with a new function g, where g(x) = 3
x
+ x
2
− 5. Convince yourself
that if f (x) = 5 has a solution c, then this number c is also a solution of the
equation g(x) = 0. Since g(0) < 0 and g(2) > 0, you can use the previous
method instead of the variation! In fact, the variation doesn’t really give us
anything new—it just makes life a little easier sometimes.
5.1.5 A harder IVT example
One last example: let’s show that any polynomial of odd degree has at least
one root. That is, let p be a polynomial of odd degree; I claim that there is
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
at least one number c such that p(c) = 0. (This isn’t true for polynomials of
even degree: for example, the quadratic x
2
+ 1 doesn’t have any roots—its
graph doesn’t cross the x-axis.) So, how do we prove my claim?
The key is actually found in the methods of Section 4.3 of the previous
chapter. There we saw that if p(x) is any polynomial and a
n
x
n
is its leading
term, then
lim
x→∞
p(x)
a
n
x
n
= 1 and lim
x→−∞
p(x)
a
n
x
n
= 1.
So when x gets very large, p(x) and a
n
x
n
are relatively close to each other
(their ratio is near 1). This means that they at least have the same sign as
each other! One can’t be negative and the other positive, or else their ratio
would be negative, not close to 1. The same is true when x is a very large
negative number.
So let’s suppose that A is a large negative number, so large that p(A) and
a
n
A
n
have the same sign. Also, we’ll pick some huge positive number B so
that p(B) and a
n
B
n
have the same sign. Now let’s compare the signs of a
n
A
n
and a
n
B
n
. Since n is an odd number, these must have opposite signs! One
is negative and one is positive. For example, if a
n
> 0, then a
n
B
n
is positive
and a
n
A
n
is negative. (This is only true because n is odd: if n were even then
both quantities would be positive.) So here’s the situation:
p(A) ←→
same sign as
a
n
A
n
←→
opposite sign to
a
n
B
n
←→
same sign as
p(B).
So p(A) and p(B) have opposite signs. Since p is a polynomial, it is continuous;
by the Intermediate Value Theorem, there is a number c between A and B
such that p(c) = 0. That is, p has a root, although we really have no idea
where it is. That makes sense since we knew virtually nothing about p to
start with, only that its degree was odd.
5.1.6 Maxima and minima of continuous functions
Let’s move on to the second benefit of knowing that a function is continuous.
Suppose we have a function f which we know is continuous on the closed
interval [a, b]. (It’s very important that the interval is closed at both ends.)
That means that we put our pen down at the point (a, f(a)) and draw a curve
that ends up at (b, f (b)) without taking our pen off the paper. The question
is, how high can we go? In other words, is there any limit to how high up this
curve could go? The answer is yes: there must be a highest point, although
the curve could reach that height multiple times.
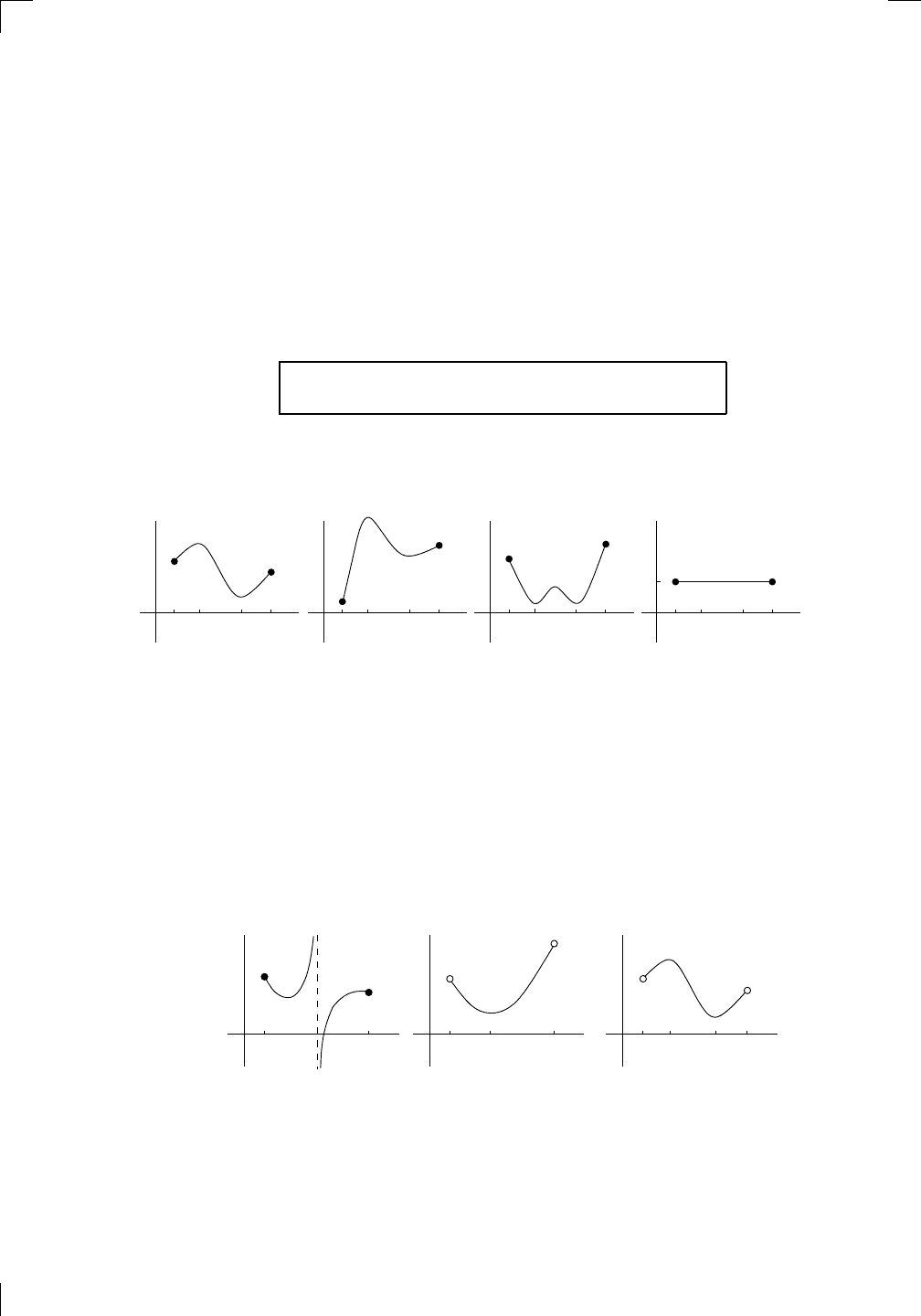
Section 5.1.6: Maxima and minima of continuous functions • 83
In symbols, let’s say that the function f defined on the interval [a, b] has a
maximum at x = c if f (c) is the highest value of f on the whole interval [a, b].
That is, f(c) ≥ f(x) for all x in the interval. The idea that I’ve been driving
at is that a continuous function on [a, b] has a maximum in the interval [a, b].
The same is true for the limbo question, “how low can you go?” We’ll say
that f has a minimum at x = c if f(c) is the lowest value of f on the whole
interval; that is, that f(c) ≤ f (x) for all x in [a, b]. Once again, any continuous
function on the interval [a, b] has a minimum in that interval. These facts form
a theorem, sometimes known as the Max-Min Theorem, which can be stated
as follows:
Max-Min Theorem: if f is continuous on [a, b], then
f has at least one maximum and one minimum on [a, b].
Here are some examples of continuous functions on [a, b] and their maxima
and minima (these are the plurals of maximum and minimum, respectively,
of course):
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
aaaa bbbb cccc ddd d
C
In the first graph, the function attains its maximum at x = c and its minimum
at x = d. In the second, the function has a maximum at x = c but the
minimum is at the left endpoint x = a. The third graph has a maximum at
x = b but the minimum is at both x = c and x = d. This is acceptable—
there are allowed to be multiple minima, as long as there is at least one.
Finally, the fourth graph shows a constant function, which is continuous; in
fact, every point in the interval [a, b] is both a maximum and a minimum,
since the function never goes above or below the constant value C.
So, why does the function f need to be continuous? And why can’t it
be an open interval, like (a, b)? The following diagrams show some potential
problems:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a aa
b bb
cc d
In the first figure, the function f has an asymptote in the middle of the interval
[a, b], which certainly creates a discontinuity. The function has no maximum
value—it just keeps going up and up on the left side of the asymptote. Sim-
ilarly, it has no minimum value either, since it just plummets way down on
the right side of the asymptote.

84 • Continuity and Differentiability
The middle diagram on the previous page involves a more subtle situation.
Here the function is only continuous on the open interval (a, b). It clearly has
a minimum at x = c, but what is the maximum of this function? You might
think that it occurs at x = b, but think again. The function isn’t even defined
at x = b! So it can’t have a maximum there. If the function has a maximum,
it must be somewhere near b. In fact, you’d like it to be the number less than
b which is closest to b. Unfortunately, there is no such number! Whatever you
think the closest number is, you can always take the average of this number
and b to get an even closer number. So there is no maximum; this illustrates
that the interval of continuity has to be closed in order to guarantee that the
Max-Min Theorem works.
Of course, the conclusion of the theorem could still be true even if the
interval isn’t closed. For example, the function in the third diagram above
is only continuous on the open interval (a, b), but it still has a maximum at
x = c and a minimum at x = d. This was just a lucky accident: you can only
use the theorem to guarantee the existence of a maximum and minimum in
an interval [a, b] if you know the function is continuous on the entire closed
interval.
5.2 Differentiability
We’ve spent a while looking at continuity. Now it’s time to look at another
degree of smoothness that a function can have: differentiability. This essen-
tially means that the function has a derivative. So, we’ll spend quite a bit
of time looking at derivatives. One of the original inspirations for develop-
ing calculus came from trying to understand the relationship between speed,
distance, and time for moving objects. So let’s start there and work our way
back to functions later on.
5.2.1 Average speed
Imagine looking at a photo of a car on a highway. The exposure time was
very short, so it’s not blurry—you can’t even tell whether the car was moving
or not. Now, I ask you this: how fast was the car moving when the picture
was taken? No problem, you say—just use the classic formula
speed =
distance
time
.
The problem is that the photo conveys no sense of distance (the car hasn’t
moved) or time (the photo essentially captures an instant of time). So you
can’t answer my question.
Ah, but what if I tell you that a minute after the picture was taken, the
car had traveled one mile? Then you could use the above formula to see that
the car was going at a mile a minute, or 60 mph. Still, how do you know
that the car was going the same speed for that whole minute? It might have
accelerated and decelerated many times during that minute. You have no
idea how fast it was actually going at the beginning of that minute. In fact,
the above formula isn’t really accurate: the left-hand side should say average
speed , since that’s all we’ve found.
Section 5.2.2: Displacement and velocity • 85
OK, I’ll take pity on you and tell you that the car went 0.25 miles in the
first 10 seconds. Now you can use the formula and see that the average speed
over the first 10 seconds is 1.5 miles per minute, or 90 mph. This helps, but
the car could still have changed its speed over the 10 seconds—we don’t really
know how fast it was going at the beginning of the period. It’s unlikely that
it was too far away from 90 mph because the car can only accelerate and
decelerate so much in such a short time.
It would be even better to know how far the car went in 1 second after the
photo was taken, but it would still not be perfect. Even 0.0001 seconds might
be enough for the car’s speed to change, but not by much. If you sensed that
we’re heading toward whipping out a limit, you’d be quite right. We need to
look at the concept of velocity first, though.
5.2.2 Displacement and velocity
Imagine that the car is driving down a long straight highway. The mile mark-
ers are a little weird—there’s a 0 marker at some point, and to the left of it,
the markers start at −1 and become more and more negative. To the right
of the 0 marker, they go as normal. In fact, the whole situation looks exactly
like a number line:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f(x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
Suppose that the car starts at mile 2 and goes directly to mile 5. Then it
has gone a distance of 3 miles. If instead it starts at mile 2 but goes left to
mile −1, it’s also gone a distance of 3 miles. We’d like to distinguish between
these two cases, so we’ll use displacement instead of distance. The formula
for displacement is just
displacement = (final position) − (initial position).
If the car goes from position 2 to 5, then the displacement is 5 −2 = 3 miles.
If instead the car goes from 2 to −1, the displacement is (−1)−2 = −3 miles.
So displacement can be negative, unlike distance. In fact, if the displacement
is negative, then the car ends up to the left of where it began.
Another important difference between distance and displacement is that
the displacement only involves the final and initial positions—what the car
does in between is irrelevant. If it went from 2 to 11 and then back to 5, the
distance is 9 + 6 = 15 miles but the total displacement is still only 3 miles. If
instead it went from 2 to −4 and then back to 2, the displacement is actually
0 miles even though the distance is 12 miles. It is true, however, that if the
car just goes in one direction without backtracking, then the distance is the
absolute value of the displacement.
As we saw in the last section, average speed is the distance traveled divided
by the time taken. If you replace distance by displacement, you get the average
velocity instead. That is,
average velocity =
displacement
time
.
