Banner A. The Calculus Lifesaver: All the Tools You Need to Excel at Calculus
Подождите немного. Документ загружается.



C h a p t e r 4
How to Solve Limit Problems Involving Polynomials
In the previous chapter, we looked at limits from a mostly conceptual view-
point. Now it’s time to see some of the techniques used to evaluate limits.
For the moment, we’ll concentrate on limits involving polynomials; later on
we’ll see how to deal with trig functions, exponentials, and logarithms. As
we’ll see in the next chapter, differentiation involves taking limits of ratios, so
most of our focus will be on this type of limit.
When you’re taking the limit of a ratio of two polynomials, it’s really im-
portant to notice where the limit is being taken. In particular, the techniques
for dealing with x → ∞ and x → a (for some finite a) are completely different.
So, we’ll split up our plan of attack into limits involving the following types
of functions:
• rational functions as x → a;
• functions involving square roots as x → a;
• rational functions as x → ∞;
• ratios of polynomial-like (or “poly-type”) functions as x → ∞;
• rational functions/poly-type functions as x → −∞; and
• functions involving absolute values.
4.1 Limits Involving Rational Functions as x → a
Let’s start off with limits that look like this:
lim
x→a
p(x)
q(x)
,
where p and q are polynomials and a is a finite number. (Remember that
the quotient p(x)/q(x) of two polynomials is called a rational function.) The
first thing you should always try is to substitute the value of a for x. If the
denominator isn’t 0, then you’re in good shape—the value of the limit is just
what you get when you substitute. For example, what is
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−3π
−
5π
2
−2π
−
3π
2
−π
−
π
2
3π
5π
2
2π
2π
3π
2
π
π
2
y = sin(x)
y = cos(x)
−
π
2
π
2
y = tan(x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(x)
−2π
−3π
−
5π
2
−
3π
2
−π
−
π
2
π
2
3π
3π
5π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
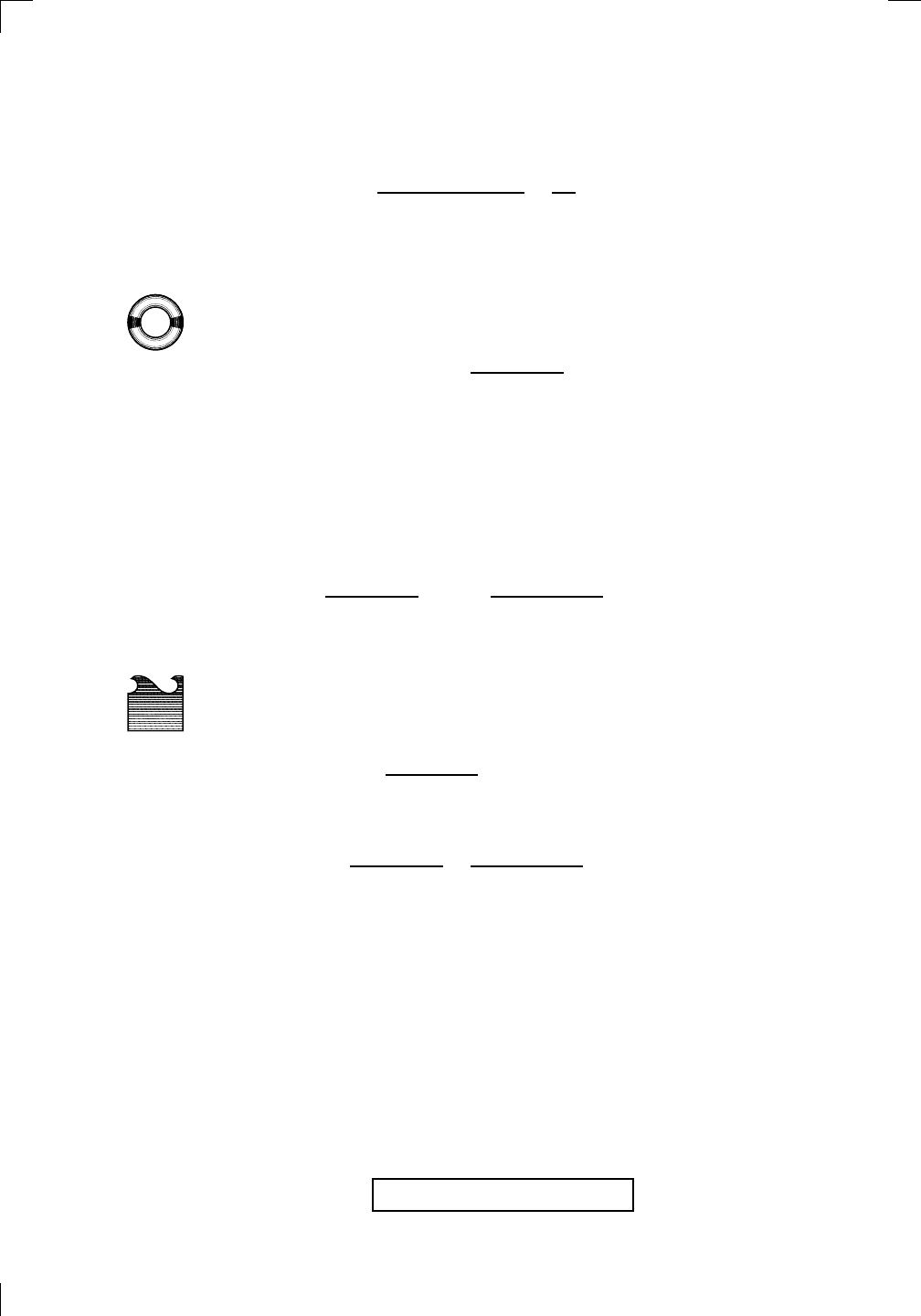
lim
x→−1
x
2
− 3x + 2
x − 2
?
58 • How to Solve Limit Problems Involving Polynomials
Simply plug x = −1 into the expression (x
2
− 3x + 2)/(x − 2), and you get
(−1)
2
− 3(−1) + 2
−1 − 2
=
6
−3
= −2.
The denominator isn’t 0, so −2 is the value of the limit. (I know that I said in
the previous chapter that the value of the function at the limit point, which
is x = −1 in this case, is irrelevant; but in the next chapter we’ll look at the
concept of continuity, which will justify this “plugging-in” method.)
On the other hand, if you want to find
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x→2
x
2
− 3x + 2
x − 2
,
then plugging in x = 2 won’t work so well: you get (4 −6 + 2)/(2 −2), which
simplifies down to 0/0. This is called an indeterminate form. If you use the
plugging in method and get zero divided by zero, then anything could happen:
the limit might be finite, the limit might be ∞ or −∞, or the limit might
not exist. The above example can be solved by the important technique of
factoring everything in sight. In particular, x
2
− 3x + 2 can be factored as
(x − 2)(x − 1), so we can write
lim
x→2
x
2
− 3x + 2
x − 2
= lim
x→−2
(x − 2)(x − 1)
x − 2
= lim
x→2
(x − 1)
by canceling. Now there’s no impediment to plugging x = 2 into the ex-
pression (x − 1); you just get 2 − 1, which equals 1. That’s the value of our
limit.
This brings us to a point which is often misunderstood: are the two func-
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(x)
−2π
−3π
−
5π
2
−
3π
2
−π
−
π
2
π
2
3π
3π
5π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
tions f and g defined by
f(x) =
x
2
− 3x + 2
x − 2
and g(x) = x − 1
the same function? Why can’t you say that
f(x) =
x
2
− 3x + 2
x − 2
=
(x − 2)(x − 1)
x − 2
= x − 1 = g(x)?
Well, you almost can! The only problem is when x = 2, because then the
denominator (x − 2) is equal to 0 and that doesn’t make sense. So f and g
are not the same function: the number 2 is not in the domain of f but it is in
the domain of g. (We’ve actually encountered this function f before—check
out the discussion and graph at the beginning of Chapter 3.) On the other
hand, if you put limits in front of everything in the above chain of equations,
it all becomes correct because the values of f(x) and g(x) at x = 2 don’t
matter—it’s only the values of f (x) and g(x) near x = 2 that count. So the
solution of the previous limit problem is indeed valid.
Let’s look at another example of an indeterminate form. Again, the tech-
nique is to try to factor everything in sight. In addition to knowing how to
factor quadratics, it’s really useful to know the formula for the difference of
two cubes:
a
3
− b
3
= (a − b)(a
2
+ ab + b
2
).

Section 4.1: Limits Involving Rational Functions as x → a • 59
Here’s a harder example where you need to use this formula: find
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x→3
x
3
− 27
x
4
− 5x
3
+ 6x
2
.
If you plug in x = 3, you indeed get 0/0 (try it and see). So let’s try to factor
both the numerator and the denominator. The numerator is the difference
between x
3
and 3
3
, so we can use the boxed formula above. The denomi-
nator has an obvious factor of x
2
, so it can be written as x
2
(x
2
− 5x + 6).
The quadratic x
2
− 5x + 6 can also be factored; altogether, then, you should
convince yourself that we have
lim
x→3
x
3
− 27
x
4
− 5x
3
+ 6x
2
= lim
x→3
(x − 3)(x
2
+ 3x + 9)
x
2
(x − 3)(x − 2)
.
Substituting x = 3 doesn’t work because of the factor of (x − 3) in the de-
nominator. On the other hand, since we are taking limits, we only need to see
what happens when x is near 3; so we are perfectly justified in canceling out
the factors of (x − 3) from the numerator and denominator—they are never
equal to 0. So, using the plugging-in technique after factoring and canceling,
the whole solution looks like this:
lim
x→3
x
3
− 27
x
4
− 5x
3
+ 6x
2
= lim
x→3
(x − 3)(x
2
+ 3x + 9)
x
2
(x − 3)(x − 2)
= lim
x→3
x
2
+ 3x + 9
x
2
(x − 2)
=
3
2
+ 3 · 3 + 9
3
2
(3 − 2)
= 3.
What if the denominator is 0 but the numerator isn’t 0? In that case,
there’s always a vertical asymptote involved; that is, the graph of the rational
function will have a vertical asymptote at the value of x that you’re interested
in. The problem is that there are four types of behavior that could arise. In
each of the following diagrams, f is the rational function we care about, and
the various limits at x = a are shown under the picture:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−π
−
π
2
3π
3π
5π
2
2π
3π
2
π
π
2
y = sin(x)
1
0
−1
−3π
−
5π
2
−2π
−
3π
2
−π
−
π
2
3π
5π
2
2π
2π
3π
2
π
π
2
y = sin(x)
y = cos(x)
−
π
2
π
2
y = tan(x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(x)
−2π
−3π
−
5π
2
−
3π
2
−π
−
π
2
π
2
3π
3π
5π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f (x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞lim
x →a
+
f(x) = ∞ lim
x →a
+
f(x) = −∞lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞lim
x →a
−
f(x) = ∞ lim
x →a
−
f(x) = −∞lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞ lim
x →a
f(x) = −∞lim
x →a
f(x) DNElim
x →a
f(x) DNE
y = f (x)y = f (x)y = f (x)y = f (x)
aaaa
So, how do you tell which of the four cases you’re dealing with? You just
have to explore the sign of f(x) on either side of x = a. If it’s positive on
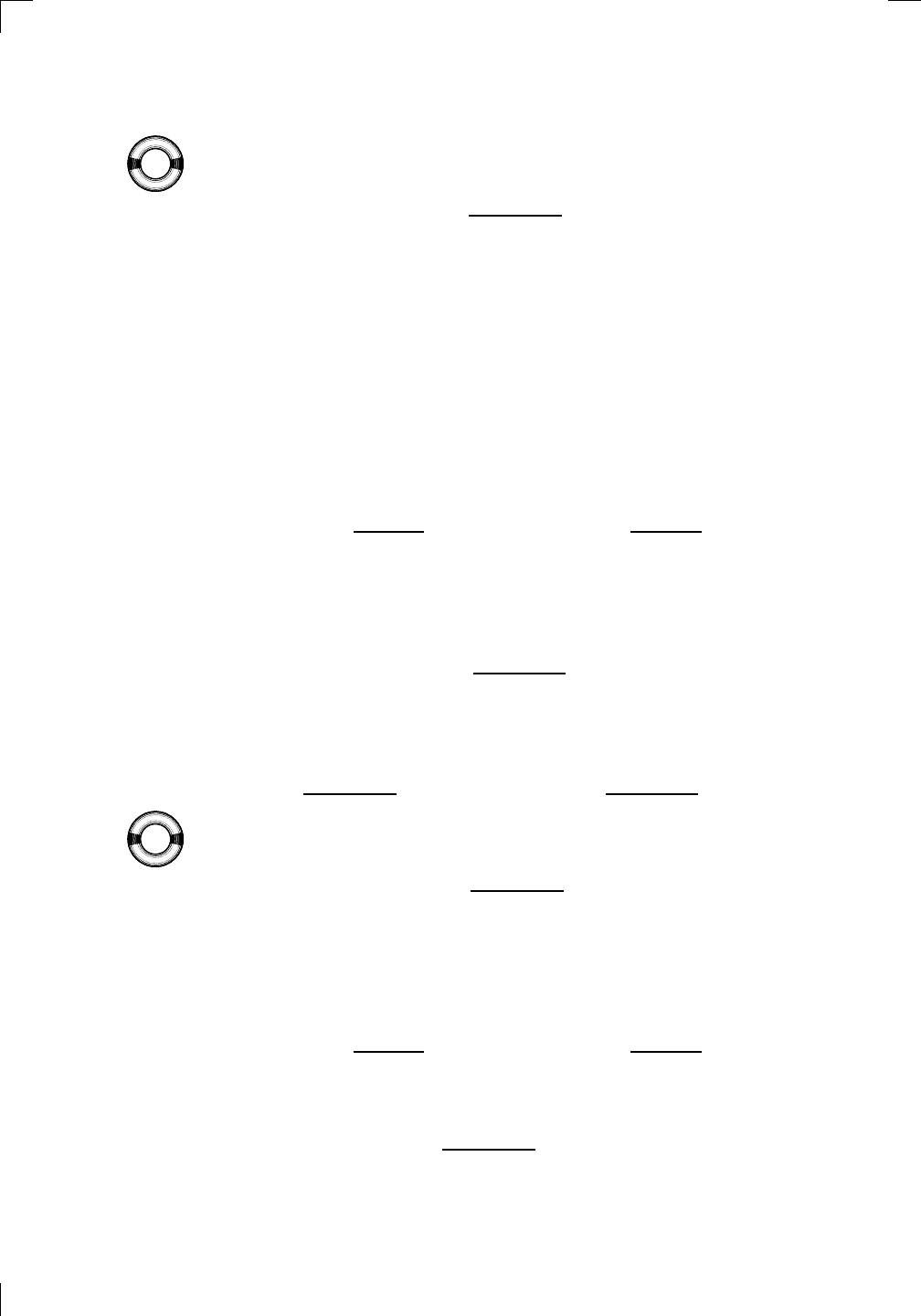
60 • How to Solve Limit Problems Involving Polynomials
both sides, for example, then you must be in the second case above. Here’s
an actual example: how would you find
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
lim
x→1
2x
2
− x − 6
x(x − 1)
3
?
First, plugging in x = 1 gives −5/0 (try it!). So we must be dealing with one of
the four cases above. Which one? Let’s set f(x) = (2x
2
− x − 6)/(x(x − 1)
3
)
and see what happens when we move x around near 1. The first thing to
notice is that the numerator 2x
2
−x − 6 is actually equal to −5 when x = 1,
so when we wobble x around a little bit, the numerator will stay negative.
How about the factor of x in the denominator? When x = 1, this factor is of
course 1, which is positive—and it stays positive when you move x around a
bit. The crucial factor is (x − 1)
3
. This is positive when x > 1 but negative
when x < 1. So we can summarize the situation like this (using (+) and (−)
to denote positive and negative quantities, respectively, and of course using
the fact that (−) · (−) = (+) and so on):
when x > 1 :
(−)
(+) · (+)
= (−); when x < 1 :
(−)
(+) · (−)
= (+).
That is, f(x) is negative when x is a little greater than 1, but positive when x
is a little less than 1. Look up at the four pictures above—the only one that
works is the third figure. In particular, we can see that the two-sided limit
lim
x→1
2x
2
− x − 6
x(x − 1)
3
does not exist, but the one-sided limits do (although they are infinite); in
particular,
lim
x→1
+
2x
2
− x − 6
x(x − 1)
3
= −∞ and lim
x→1
−
2x
2
− x − 6
x(x − 1)
3
= ∞.
Now suppose we change the limit slightly to
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−3π
−
5π
2
−
3π
2
−π
−
π
2
π
2
3π
3π
5π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
lim
x→1
2x
2
− x − 6
x(x − 1)
2
.
How does that change anything? Well, the numerator is still negative when x
is near 1, and the factor x is still positive, but how about (x −1)
2
? Since it’s
a square, it must be positive when x is near but not equal to 1. So we now
have the following situation:
when x > 1 :
(−)
(+) · (+)
= (−); when x < 1 :
(−)
(+) · (+)
= (−).
Now we have negative values on either side of x = 1, so we must have
lim
x→1
2x
2
− x − 6
x(x − 1)
2
= −∞.
Of course, the left- and right-hand limits are both equal to −∞ as well.
Section 4.2: Limits Involving Square Roots as x → a • 61
4.2 Limits Involving Square Roots as x → a
Consider the following limit:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
lim
x→5
√
x
2
− 9 − 4
x − 5
.
If you plug in x = 5, you get the indeterminate form 0/0 (try it and see!).
Trying to factor everything in sight doesn’t work so well—you can write x
2
−9
as (x−3)(x+3), but that doesn’t really help because of that blasted −4 in the
numerator. What you need to do is multiply and divide by
√
x
2
− 9 + 4; this
is called the conjugate expression of
√
x
2
− 9 −4. (You have probably already
met conjugate expressions in your math studies, especially when rationalizing
the denominator. The basic idea is that the conjugate expression of a − b is
a + b, and vice versa.) So, here’s what we get when we do this multiplication
and division:
lim
x→5
√
x
2
− 9 − 4
x − 5
= lim
x→5
√
x
2
− 9 − 4
x − 5
×
√
x
2
− 9 + 4
√
x
2
− 9 + 4
.
This looks more complicated, but something nice happens: using the formula
(a−b)(a +b) = a
2
−b
2
, the numerator simplifies to (
√
x
2
− 9)
2
−4
2
, or simply
x
2
− 25. So the above limit is just
lim
x→5
x
2
− 25
(x − 5)(
√
x
2
− 9 + 4)
.
Factor x
2
− 25 as (x − 5)(x + 5) and cancel to see that this limit becomes
lim
x→5
(x − 5)(x + 5)
(x − 5)(
√
x
2
− 9 + 4)
= lim
x→5
x + 5
√
x
2
− 9 + 4
.
Now if you substitute x = 5, there are no problems: you simply get 10/8, or
5/4. The moral of the story is that if you have a square root plus or minus
another quantity, try multiplying and dividing by its conjugate—you might
be pleasantly surprised!
4.3 Limits Involving Rational Functions as x → ∞
OK, back to rational functions, but this time we’ll look at what happens as
x → ∞ instead of some finite value. In symbols, we are now trying to find
limits of the form
lim
x→∞
p(x)
q(x)
,
where p and q are polynomials. Now, here’s a very important property of a
polynomial: when x is large, the leading term dominates. What this
means is that if you have a polynomial p, then as x gets larger and larger,
p(x) behaves as if only its leading term were present. For example, let’s say
p(x) = 3x
3
− 1000x
2
+ 5x − 7. Let’s put p
L
(x) = 3x
3
, which is the leading

62 • How to Solve Limit Problems Involving Polynomials
term of p. Here’s what I’m claiming: when x is really really large, p(x) and
p
L
(x) are relatively close to each other. More precisely, we have
lim
x→∞
p(x)
p
L
(x)
= 1.
Before we see why this is true, let’s just look at the implications of what it is
saying. Imagine that the limit wasn’t there. This equation would say
p(x)
p
L
(x)
= 1,
which means that p(x) = p
L
(x). Well, that clearly isn’t true (at least for most
values of x), but the larger x is, the closer it is to being true. So why not just
write
lim
x→∞
p(x) = lim
x→∞
p
L
(x)?
This is actually true, but it’s meaningless because both sides are ∞. So we
have to settle for saying that p(x) and p
L
(x) are very close to each other in
the sense that their ratio is close to 1. As x gets large, the ratio approaches
1 without ever necessarily equaling 1.
Does this make sense? Why is it the leading term, anyway? Why not one
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
of the other terms? If you want, you can skip to the next paragraph and see
the mathematical proof; first, however, I’d like to get a feel for what happens
in our example, p(x) = 3x
3
− 1000x
2
+ 5x − 7, by testing it on actual large
values of x. Let’s start off with x = 100. In that case, 3x
3
is 3 million, while
1000x
2
is 10 million. The quantity 5x is only 500, and the 7 doesn’t make
much difference, so all together we can see that p(100) is about −7 million. On
the other hand, p
L
(100) is 3 million, so it’s not looking so great: p(100) and
p
L
(100) are completely different. Let’s not lose heart—after all, 100 isn’t that
large. Suppose we instead set x equal to 1,000,000—that’s a million. Then
3x
3
is freakin’ huge: it’s 3,000,000,000,000,000,000, or three million trillion!
In comparison, 1000x
2
is relatively puny at only a thousand trillion (that’s
1,000,000,000,000,000) and 5x is only 5 million, which is a microscopic speck
of dust in comparison to these numbers. The −7 term is just laughable and
makes no noticeable difference. So, to calculate p(1,000,000), we need to take
3 million trillion and take away a thousand trillion plus some spare change (a
little under 5 million). Let’s face it, it’s still darned close to 3 million trillion!
After all, how many trillions are we dealing with here? We have 3 million of
them, and we’re taking away a mere one thousand of them, so we still have
almost 3 million trillions. That is, p(1,000,000) is about 3 million trillion—but
that is exactly the value of p
L
(1,000,000). The point is that the highest-degree
term is growing much faster than the other terms as x gets large. Indeed, if
you replace 1,000,000 with an even larger number, the difference between x
3
and the lower order terms like x
2
and x becomes even more pronounced.
Enough philosophical rambling. Let’s try to give a real proof that
lim
x→∞
p(x)
p
L
(x)
= 1.
We have to do some actual math. Start off by writing
lim
x→∞
p(x)
p
L
(x)
= lim
x→∞
3x
3
− 1000x
2
+ 5x − 7
3x
3
Section 4.3: Limits Involving Rational Functions as x → ∞ • 63
which simplifies to
lim
x→∞
3x
3
3x
3
−
1000x
2
3x
3
+
5x
3x
3
−
7
3x
3
= lim
x→∞
1 −
1000
3x
+
5
3x
2
−
7
3x
3
.
How do you handle this? Well, the first thing to note is that you can bust up
this last expression into four separate limits. So if you know what happens
to the four quantities 1, −1000/3x, 5/3x
2
, and −7/3x
3
as x becomes very
large, then you can just add the four limits together to get the limit you
want. Technically, this could be described in words as “the limit of the sum
is equal to the sum of the limits”; this is true when all the limits are finite.
∗
So, we have four quantities to worry about. The first is 1, which is always 1
regardless of what happens to x. The second quantity is −1000/3x. What
happens to this when x gets large? That is, what is
lim
x→∞
−
1000
3x
?
The trick here is to realize that you can take out a factor of −1000/3. In
particular, the limit can be expressed as
lim
x→∞
−
1000
3
1
x
.
The cool thing about something like −1000/3 is that it’s constant. It doesn’t
change, no matter what x is, so it turns out that you can just go ahead and
drag it out of the limit (see Section A.2.2 of Appendix A for more details).
So we have
lim
x→∞
−
1000
3
1
x
= −
1000
3
lim
x→∞
1
x
.
We’ve already seen that the reciprocal of a very large number is a very small
number (remember, this means a number very close to zero). So lim
x →∞
1/x = 0,
and −1000/3 times the limit is also 0. The conclusion is that
lim
x→∞
−
1000
3x
= 0.
In fact, you should just write that down without going into any more detail.
More generally, you can use the following theorem:
lim
x→∞
C
x
n
= 0
for any n > 0, as long as C is constant. This fact allows us to see that the
other two pieces, 5/3x
2
and −7/3x
3
, also tend to 0 as x becomes very large.
So the whole argument is
lim
x→∞
3x
3
− 1000x
2
+ 5x − 7
3x
3
= lim
x→∞
1 −
1000
3x
+
5
3x
2
−
7
3x
3
= 1 − 0 + 0 + 0 = 1.
∗
It’s not true if the limits aren’t finite! Consider lim
x →∞
(x + (1 −x)). For any x, it’s true
that (x + (1 − x)) = 1, so this limit is just 1. On the other hand, the individual limits of
the two pieces (x) and (1 − x) are lim
x →∞
(x) and lim
x →∞
(1 − x). The first limit is ∞ and the
second is −∞, but it’s not true that ∞ + (−∞) = 1. In fact, the expression ∞ + (−∞) is
meaningless.

64 • How to Solve Limit Problems Involving Polynomials
So we have proved that
lim
x→∞
p(x)
leading term of p(x)
= 1
in the special case where p(x) = 3x
3
− 1000x
2
+ 5x − 7. Luckily the same
method works for any polynomial, and we’ll be using it over and over again
during the rest of this chapter!
4.3.1 Method and examples
Here’s the general idea: when you see p(x) for some polynomial p with more
than one term, replace it by
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
p(x)
leading term of p(x)
× (leading term of p(x)).
Do this for every polynomial around! Note that all we’ve done is to divide
and multiply by the leading term, so we haven’t changed the quantity p(x).
The point is that the fraction in the expression above has limit 1 as x → ∞,
and the leading term is much simpler. Let’s see how this works in practice:
for example, what is
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
lim
x→∞
x − 8x
4
7x
4
+ 5x
3
+ 2000x
2
− 6
?
We have two polynomials: one on the top and one on the bottom. For the
numerator, the leading term is −8x
4
(don’t be fooled by the order in which
the numerator is written—the leading term isn’t always written first!). So
we’re going to replace the numerator by
x − 8x
4
−8x
4
× (−8x
4
).
Similarly, the denominator has leading term 7x
4
, so we’ll replace it by
7x
4
+ 5x
3
+ 2000x
2
− 6
7x
4
× (7x
4
).
Making both these replacements leads to this:
lim
x→∞
x − 8x
4
7x
4
+ 5x
3
+ 2000x
2
− 6
= lim
x→∞
x − 8x
4
−8x
4
× (−8x
4
)
7x
4
+ 5x
3
+ 2000x
2
− 6
7x
4
× (7x
4
)
.
Looking at this, you should concentrate on the ratio
−8x
4
7x
4
,
because that’s what’s really going on here. The other fractions all have limit
1, but we have effectively squeezed all the important juice out of our two
polynomials into the simple ratio of leading terms. Luckily that ratio just
Section 4.3.1: Method and examples • 65
simplifies to −8/7, so that should be our answer. To nail that down, we have
to prove that the other fractions have limit 1, but that’s no problem. You
see, in each of the little fractions, we can do the division and we see that our
above limit can be written as
lim
x→∞
−
1
8x
3
+ 1
1 +
5
7x
+
2000
7x
2
−
6
7x
4
×
−8x
4
7x
4
.
Now we take limits; from the fact in the box in the previous section, any
expression of the form C/x
n
goes to 0 as x → ∞ (provided that C is constant
and n > 0). So most of the stuff goes away! We also cancel out the x
4
factor
on the right to see that we are reduced to
0 + 1
1 + 0 + 0 − 0
×
−8
7
=
1
1
×
−8
7
=
−8
7
and we’re all done.
Here’s another example: find
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
lim
x→∞
(x
4
+ 3x − 99)(2 − x
5
)
(18x
7
+ 9x
6
− 3x
2
− 1)(x + 1)
.
We have four polynomials here, with leading terms x
4
, −x
5
, 18x
7
, and x. So
we’ll use our method for each one of them! Try it and see for yourself before
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
reading further. Even if you don’t, make sure you understand every step of
the argument below:
lim
x→∞
(x
4
+ 3x − 99)(2 − x
5
)
(18x
7
+ 9x
6
− 3x
2
− 1)(x + 1)
= lim
x→∞
x
4
+ 3x − 99
x
4
× (x
4
)
2 − x
5
−x
5
× (−x
5
)
18x
7
+ 9x
6
− 3x
2
− 1
18x
7
× (18x
7
)
x + 1
x
× (x)
= lim
x→∞
1 +
3
x
3
−
99
x
4
−
2
x
5
+ 1
1 +
9
18x
−
3
18x
5
−
1
18x
7
1 +
1
x
×
(x
4
)(−x
5
)
(18x
7
)(x)
=
(1 + 0 − 0)(0 + 1)
(1 + 0 − 0 − 0)(1 + 0)
× lim
x→∞
−x
18
= lim
x→∞
−x
18
= −∞.
The main point is that we boiled out the leading terms into the ratio
(x
4
)(−x
5
)
(18x
7
)(x)
,
which simplifies to −x/18. Everything else had no effect! Finally, when
x → ∞, the quantity −x/18 goes to −∞, so that’s the “value” of the limit
we’re looking for.
