Banner A. The Calculus Lifesaver: All the Tools You Need to Excel at Calculus
Подождите немного. Документ загружается.


66 • How to Solve Limit Problems Involving Polynomials
In the previous two examples, we’ve seen that the limit might be finite and
nonzero (we got the answer −8/7) or it might be infinite (we got the answer
−∞). Let’s look at the degree of the polynomials in these examples. In the
first example, both the numerator and the denominator were of degree 4. In
the second example, the numerator is the product of polynomials of degree
4 and degree 5, so if you multiply it out, you get a polynomial of degree
9. Similarly, the denominator is the product of polynomials of degree 7 and
degree 1, so it has total degree 8. In this case, the numerator is of greater
degree than the denominator. On the other hand, consider this limit:
lim
x→∞
2x + 3
x
2
− 7
.
Let’s use our methods to solve it:
lim
x→∞
2x + 3
x
2
− 7
= lim
x→∞
2x + 3
2x
× (2x)
x
2
− 7
x
2
× (x
2
)
= lim
x→∞
1 +
3
2x
1 −
7
x
2
×
2x
x
2
=
1 + 0
1 − 0
× lim
x→∞
2
x
= 0.
Here, the denominator has degree 2, which is greater than the numerator’s
degree (which is 1). The result is that the denominator dominates, so the
limit is 0. In general, here’s what we can say considering the limit
lim
x→∞
p(x)
q(x)
where p and q are polynomials:
1. If the degree of p equals the degree of q, the limit is finite and nonzero.
2. If the degree of p is greater than the degree of q, the limit is ∞ or −∞.
3. If the degree of p is less than the degree of q, the limit is 0.
(All this is also true when x → −∞, so that the limit is
lim
x→−∞
p(x)
q(x)
;
we’ll consider this case in Section 4.5 below.) These facts are easily proved in
general using the above methods. Useful as these facts are, you really don’t
need them to solve problems; you should use the dividing and multiplying
method, then use the facts to check that your answer makes sense.
4.4 Limits Involving Poly-type Functions as x → ∞
Consider functions f, g and h defined by
f(x) = x
3
+ 4x
2
− 5x
2/3
+ 1, g(x) =
p
x
9
− 7x
2
+ 2,
and h(x) = x
4
−
q
x
3
+
5
p
x
2
− 2x + 3.

Section 4.4: Limits Involving Poly-type Functions as x → ∞ • 67
These aren’t polynomials because they involve fractional powers or nth roots,
but they look a little like polynomials. In fact, the methods of the previous
section work on these objects as well, so I’ll call them “poly-type functions.”
The principles for poly-type functions are similar to those for polynomials,
except that this time it may not be so clear what the leading term is. The
presence of square roots (or cube roots, fourth roots, and so on) can have a
big impact on this. For example, let’s consider
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
lim
x→∞
√
16x
4
+ 8 + 3x
2x
2
+ 6x + 1
.
The bottom is a polynomial with leading term 2x
2
, so we’ll replace it by
2x
2
+ 6x + 1
2x
2
× (2x
2
).
How about the top? The part under the square root is a polynomial, 16x
4
+8,
and its leading term is 16x
4
. If you take the square root of that, you get 4x
2
.
So mentally you should think of the top as behaving like 4x
2
+3x. The leading
term of that is 4x
2
, so that’s what we’re going to use. Specifically, we will
replace the top by
√
16x
4
+ 8 + 3x
4x
2
× (4x
2
).
How do you simplify the first fraction? The answer is that you can drag the
4x
2
under the square root, and it becomes 16x
4
:
√
16x
4
+ 8 + 3x
4x
2
=
√
16x
4
+ 8
4x
2
+
3x
4x
2
=
r
16x
4
+ 8
16x
4
+
3x
4x
2
.
Now if you split up more and cancel, you can reduce this to
r
1 +
8
16x
4
+
3
4x
.
As x → ∞, the parts with x on the bottom just go away, so this expression
goes to
√
1 + 0 + 0 = 1.
So, let’s put it all together and write out the solution to the original problem:
lim
x→∞
√
16x
4
+ 8 + 3x
2x
2
+ 6x + 1
= lim
x→∞
√
16x
4
+ 8 + 3x
4x
2
× (4x
2
)
2x
2
+ 6x + 1
2x
2
× (2x
2
)
= lim
x→∞
r
16x
4
+ 8
16x
4
+
3x
4x
2
2x
2
+ 6x + 1
2x
2
×
4x
2
2x
2
= lim
x→∞
r
1 +
8
16x
4
+
3
4x
1 +
6
2x
+
1
2x
2
×
4
2
=
√
1 + 0 + 0
1 + 0 + 0
× 2 = 2.
68 • How to Solve Limit Problems Involving Polynomials
Nice, huh? Messy, but nice. Now let’s see what happens when we modify the
situation very slightly. Consider
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
lim
x→∞
√
16x
4
+ 8 + 3x
3
2x
2
+ 6x + 1
.
The only change is that the 3x term in the numerator in the previous example
has become 3x
3
. How does this affect things? Well, we already said that the
√
16x
4
+ 8 term behaves like 4x
2
for large x, but this time it gets swamped
by the higher-degree term 3x
3
. So now we have to replace the top by
√
16x
4
+ 8 + 3x
3
3x
3
× (3x
3
);
of course, when we drag 3x
3
under the square root, it will become 9x
6
. All
together, then, the solution looks like this:
lim
x→∞
√
16x
4
+ 8 + 3x
3
2x
2
+ 6x + 1
= lim
x→∞
√
16x
4
+ 8 + 3x
3
3x
3
× (3x
3
)
2x
2
+ 6x + 1
2x
2
× (2x
2
)
= lim
x→∞
r
16x
4
+ 8
9x
6
+
3x
3
3x
3
2x
2
+ 6x + 1
2x
2
×
3x
3
2x
2
= lim
x→∞
r
16
x
2
+
8
9x
6
+ 1
1 +
6
2x
+
1
2x
2
×
3x
2
=
√
0 + 0 + 1
1 + 0 + 0
× lim
x→∞
3x
2
= ∞.
Make sure you understand each step of the last two solutions. In the first
example, the leading term came from the 16x
4
under the square root; even
when you take the square root, the resulting term 4x
2
still dominated the
rest of the numerator (3x). In the second example, the rest of the numerator
(3x
3
) was the dominant force. But wait, you say—what if they are the same?
For example, what is
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3π
2
−π
−
π
2
π
2
3π
3π
5π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
lim
x→∞
√
4x
6
− 5x
5
− 2x
3
3
√
27x
6
+ 8x
?
The denominator isn’t too nasty, actually, but let’s just look at the numerator
for a second. Under the square root, we have 4x
6
− 5x
5
, which behaves like
its leading term 4x
6
when x is large. So we should think that
√
4x
6
− 5x
5
behaves like
√
4x
6
, which is just 2x
3
(since x is positive). The problem is
that we are taking away 2x
3
in the numerator, so it looks like we’re left with
nothing! Crap. What do we do?
The solution is to use the same technique as described in Section 4.2 above:
multiply top and bottom by the conjugate expression of the numerator. So
before we even look at leading terms, we need to do some prep work:
lim
x→∞
√
4x
6
− 5x
5
− 2x
3
3
√
27x
6
+ 8x
= lim
x→∞
√
4x
6
− 5x
5
− 2x
3
3
√
27x
6
+ 8x
×
√
4x
6
− 5x
5
+ 2x
3
√
4x
6
− 5x
5
+ 2x
3
.
Now the formula (a−b)(a +b) = a
2
−b
2
allows us to simplify this whole thing
to
lim
x→∞
(4x
6
− 5x
5
) − (2x
3
)
2
3
√
27x
6
+ 8x(
√
4x
6
− 5x
5
+ 2x
3
)
.
Section 4.4: Limits Involving Poly-type Functions as x → ∞ • 69
In fact we can even tidy up the numerator further and reduce the situation to
lim
x→∞
−5x
5
3
√
27x
6
+ 8x(
√
4x
6
− 5x
5
+ 2x
3
)
.
There, that’s not so bad! There’s nothing we need to do on the numerator;
let’s just concentrate on the denominator. For
3
√
27x
6
+ 8x, we can actually
just multiply and divide by the cube root of the leading term 27x
6
, giving
3
√
27x
6
+ 8x
3
√
27x
6
×
3
√
27x
6
,
which is just
3
√
27x
6
+ 8x
3
√
27x
6
× (3x
2
).
Of course, we’ll combine the terms under the square root and cancel to get
3
r
27x
6
+ 8x
27x
6
× (3x
2
) =
3
r
1 +
8
27x
5
× (3x
2
).
Note that the part involving the cube root just goes to 1 as x → ∞.
As for the other term,
√
4x
6
− 5x
5
+2x
3
, here we need to be a little careful.
Under the square root, we have 4x
6
− 5x
5
, so the leading term is 4x
6
. The
square root of this is 2x
3
. Now we have to add 2x
3
to this, and the total
“leading term” on the numerator is therefore 2x
3
+ 2x
3
, or 4x
3
. Let’s see how
it works. We’ll replace the numerator by
√
4x
6
− 5x
5
+ 2x
3
4x
3
× (4x
3
),
then split up the fraction and drag the 4x
3
under the square root, where it
becomes 16x
6
; we get
r
4x
6
− 5x
5
16x
6
+
2x
3
4x
3
!
× (4x
3
) =
r
1
4
−
5
16x
+
1
2
!
× (4x
3
).
Now when you let x → ∞, the first product goes to
r
1
4
+ 0 +
1
2
=
1
2
+
1
2
= 1,
which is what we want! (Note that the square root of
1
4
is
1
2
.)
Now let’s try to put it all together and solve this darned problem. We
started off by multiplying the numerator by its conjugate, which reduced
matters to
lim
x→∞
−5x
5
3
√
27x
6
+ 8x(
√
4x
6
− 5x
5
+ 2x
3
)
.
Now we’ll use the multiply and divide method on the bottom, giving
lim
x→∞
−5x
5
3
√
27x
6
+ 8x
3
√
27x
6
× (3x
2
)
!
√
4x
6
− 5x
5
+ 2x
3
4x
3
× (4x
3
)
!
.
70 • How to Solve Limit Problems Involving Polynomials
Pull out the quantities −5x
5
, 3x
2
, and 4x
3
to get
lim
x→∞
1
3
√
27x
6
+ 8x
3
√
27x
6
!
√
4x
6
− 5x
5
+ 2x
3
4x
3
!
×
−5x
5
(3x
2
)(4x
3
)
.
Now all you have to do is cancel x
5
from the top and the bottom and use the
arguments from above to show that the final answer is −5/12. I’ve left you
with a bit of work, but you should try to assemble all the bits and pieces from
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
above into a complete solution.
4.5 Limits Involving Rational Functions as x → −∞
Now let’s spend a little time on limits of the form
lim
x→−∞
p(x)
q(x)
,
where p and q are polynomials or even poly-type functions. All the principles
we’ve been using apply equally well here. When x is a very large negative
number, the highest-degree term in any sum still dominates. Also, it’s true
that C/x
n
still goes to 0 as x → −∞, provided that C is constant and n
is a positive integer. (Can you see why?) This all means that the solutions
are almost identical to what we’ve already seen. For example, consider some
adaptations of two examples we’ve already looked at in Section 4.3.1 above:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3π
3π
5π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
lim
x→−∞
x − 8x
4
7x
4
+ 5x
3
+ 2000x
2
− 6
and lim
x→−∞
(x
4
+ 3x − 99)(2 − x
5
)
(18x
7
+ 9x
6
− 3x
2
− 1)(x + 1)
.
All I’ve done is change ∞ to −∞, so that we are now interested in what
becomes of the two rational functions when x is a very large negative number.
The solution to the first one is the same as it was when x tended to ∞; you
just multiply and divide by the leading term of each polynomial:
lim
x→−∞
x − 8x
4
7x
4
+ 5x
3
+ 2000x
2
− 6
= lim
x→−∞
x − 8x
4
−8x
4
× (−8x
4
)
7x
4
+ 5x
3
+ 2000x
2
− 6
7x
4
× (7x
4
)
= lim
x→−∞
−
1
8x
3
+ 1
1 +
5
7x
+
2000
7x
2
−
6
7x
4
×
−8
7
= −
8
7
.
The point here is that any term that looks like C/x
n
for some positive n goes
to 0 as x → −∞, just the same as it does when x → ∞. On the other hand,
the second example is not quite identical; the very last step is different from

Section 4.5: Limits Involving Rational Functions as x → −∞ • 71
the previous version of the problem:
lim
x→−∞
(x
4
+ 3x − 99)(2 − x
5
)
(18x
7
+ 9x
6
− 3x
2
− 1)(x + 1)
= lim
x→−∞
x
4
+ 3x − 99
x
4
× (x
4
)
2 − x
5
−x
5
× (−x
5
)
18x
7
+ 9x
6
− 3x
2
− 1
18x
7
× (18x
7
)
x + 1
x
× (x)
= lim
x→−∞
1 +
3
x
3
−
99
x
4
−
2
x
5
+ 1
1 +
9
18x
−
3
18x
5
−
1
18x
7
1 +
1
x
×
(x
4
)(−x
5
)
(18x
7
)(x)
=
(1 + 0 − 0)(−0 + 1)
(1 + 0 − 0 − 0)(1 + 0)
× lim
x→−∞
−x
18
= lim
x→−∞
−x
18
= ∞.
Only when we take the limit at the very end do we see anything different from
when x → ∞: as x → −∞, now −x/18 goes to ∞ rather than −∞.
There’s only one other thing you have to beware. We’ve been dragging
factors into square roots without being too careful. To show you what I
mean, try simplifying
√
x
2
. Did you get x? That’s not right if x is negative,
unfortunately. For example, if you square −2 and then take the square root,
you will get 2. So in fact
√
x
2
= −x when x is negative. This sort of thing
comes up when you look at poly-type limits as x → −∞, for example:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
lim
x→−∞
√
4x
6
+ 8
2x
3
+ 6x + 1
.
The denominator behaves like its leading term 2x
3
, but how about the nu-
merator? The term in the square root, 4x
6
+ 8, behaves like 4x
6
, so
√
4x
6
+ 8
behaves like
√
4x
6
. Tempting as it is to simplify this as 2x
3
, it is simply
not correct! Since x → −∞, we are interested in what happens when x is
negative. This means that 2x
3
is negative, but
√
4x
6
is positive, so we must
simplify
√
4x
6
as −2x
3
. Here’s how the solution goes:
lim
x→−∞
√
4x
6
+ 8
2x
3
+ 6x + 1
= lim
x→−∞
√
4x
6
+ 8
√
4x
6
×
√
4x
6
2x
3
+ 6x + 1
2x
3
× (2x
3
)
= lim
x→−∞
r
4x
6
+ 8
4x
6
2x
3
+ 6x + 1
2x
3
×
√
4x
6
2x
3
= lim
x→−∞
r
1 +
8
4x
6
1 +
6x
2x
3
+
1
2x
3
×
−2x
3
2x
3
=
√
1 + 0
1 + 0 + 0
× (−1) = −1.
You have to exercise similar care when you deal with fourth roots, sixth roots,
and so on. For example,
4
√
x
4
= −x if x is negative.
72 • How to Solve Limit Problems Involving Polynomials
The same would be true if you replaced every instance of 4 with any even
number. On the other hand, it’s not true if you replace 4 by an odd number;
for example,
3
√
x
3
= x for all x (positive, negative, or zero).
One other point, though: it’s still true that
√
x
4
= x
2
even if x < 0! Why? Because x
2
can’t be negative, and
√
x
4
can’t be negative
by definition, so there can’t possibly be a minus sign! Here’s a summary of
the situation:
if x < 0 and you want to write
n
√
x
something
= x
m
, the only time you
need a minus sign in front of x
m
is when n is even and m is odd.
4.6 Limits Involving Absolute Values
Sometimes you have to deal with functions involving absolute values. Consider
this limit:
lim
x→0
−
|x|
x
.
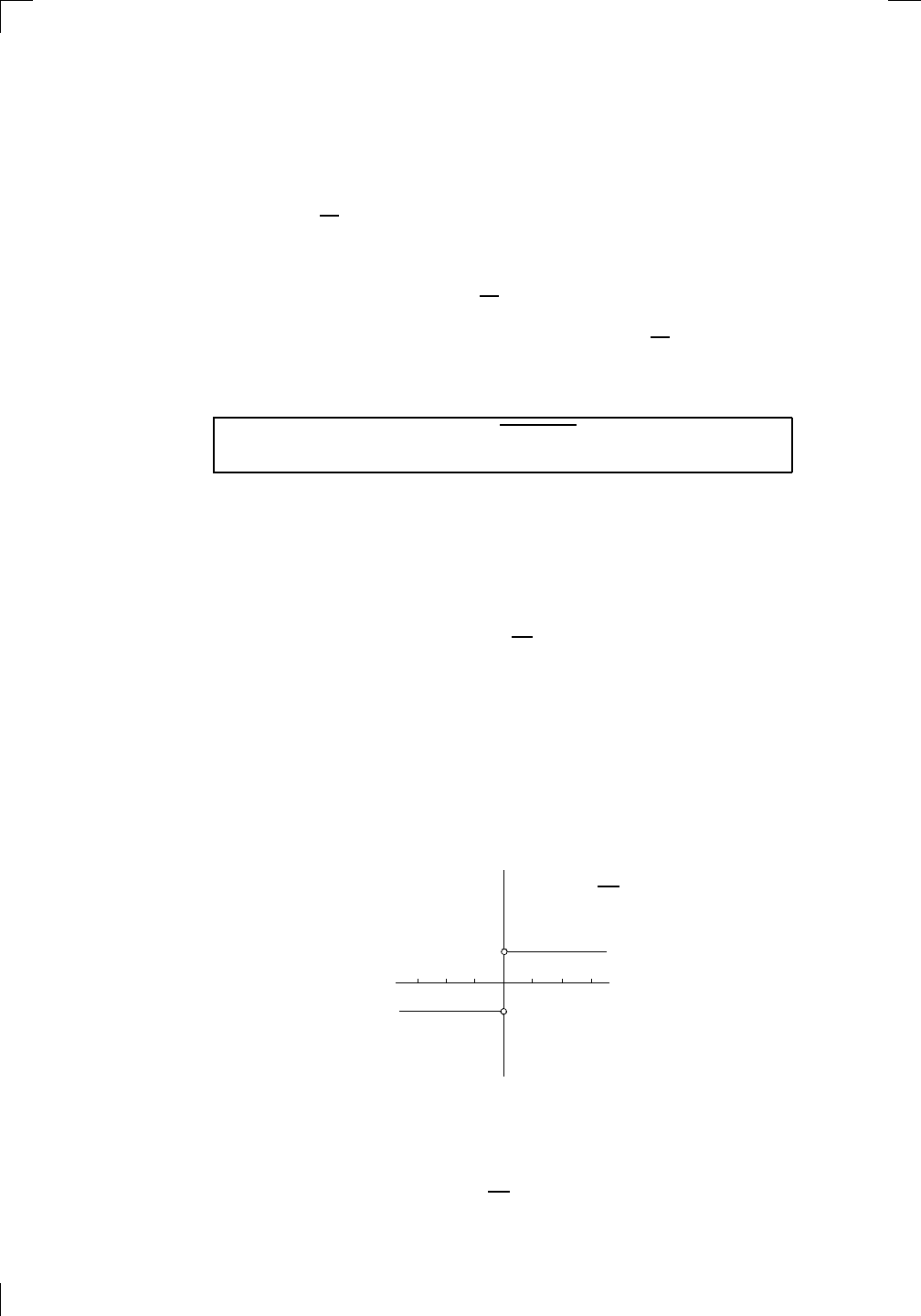
In order to answer this, let’s set f(x) = |x|/x and check it out some more.
First, note that 0 can’t be in the domain of f, since the denominator would
then be 0. On the other hand, everything else is fine. Let’s look at what
happens when x is positive. The quantity |x| is then just x, so we see that
f(x) = 1 if x is any positive number. On the other hand, if x is negative,
then |x| = −x, so f(x) = −x/x = −1 if x < 0. That is, writing f (x) = |x|/x
is just a fancy way of saying that f (x) = 1 if x > 0 and f (x) = −1 if x < 0.
The graph of y = f(x) looks like this:
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(x)
−2π
−3π
−
5π
2
−
3π
2
−π
−
π
2
π
2
3π
3π
5π
2
2π
3π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f(x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f(x)
a
y =
|x|
x
1
−1
So, for the left-hand limit that we were looking at, you need to approach x = 0
from the left, and it’s clear that
lim
x→0
−
|x|
x
= −1,
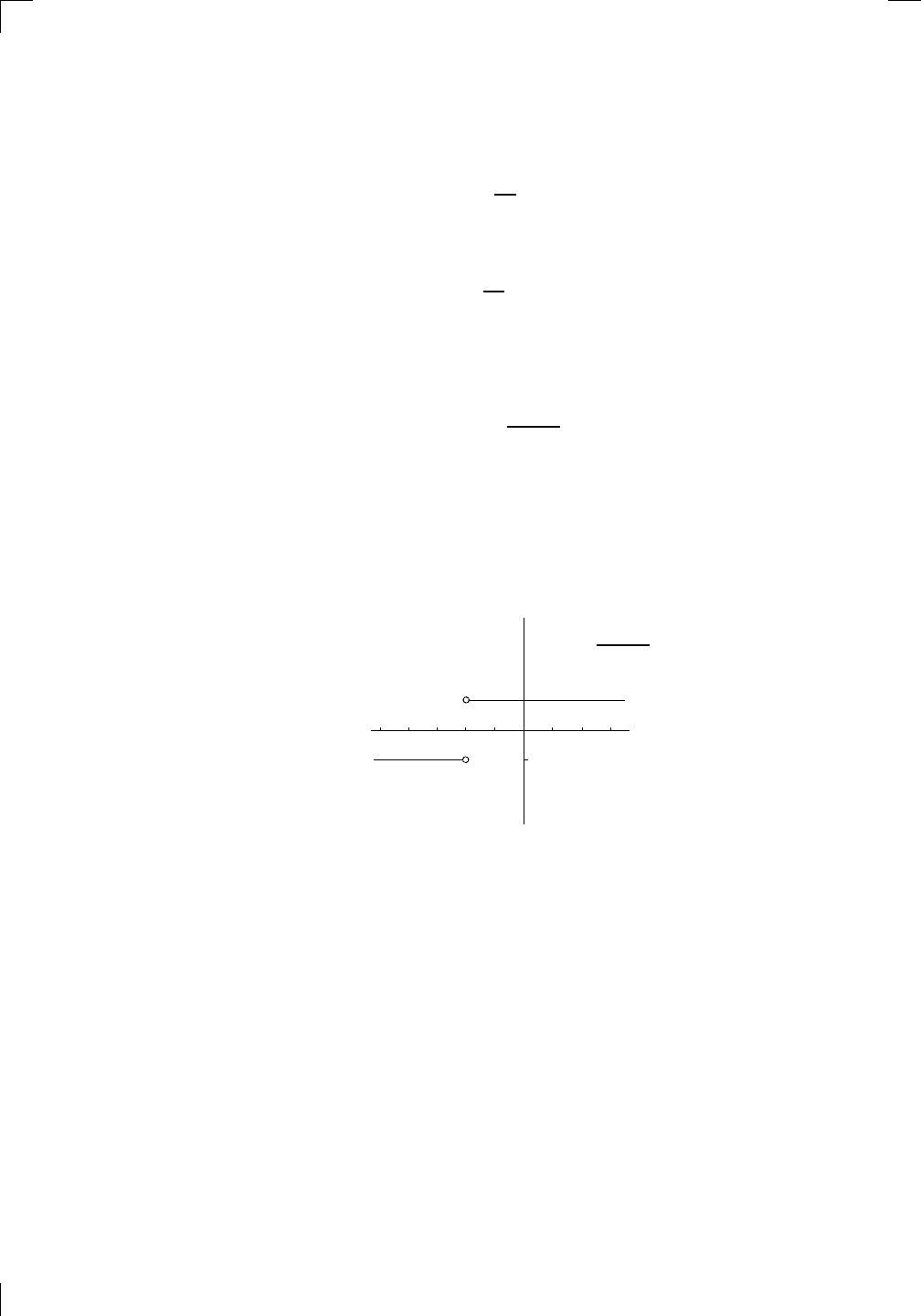
Section 4.6: Limits Involving Absolute Values • 73
and we may as well note that
lim
x→0
+
|x|
x
= 1.
Since the left- and right-hand limits don’t agree, the two-sided limit doesn’t
exist:
lim
x→0
|x|
x
DNE.
Most examples involving absolute values can be solved in a similar fashion
by considering two or more different ranges of x, depending on the sign of
what’s inside the absolute value signs. A very slight variation of the above
example is
lim
x→(−2)
−
|x + 2|
x + 2
.
Looking at the absolute value, we see that it matters whether x + 2 ≥ 0 or
x+2 < 0. These conditions can be rewritten as x ≥ −2 or x < −2. In the first
case, |x + 2| = x + 2, whereas in the second case |x + 2| = −(x + 2). The end
result is that the quantity |x + 2|/(x + 2) is equal to 1 when x > −2; whereas
the quantity is just −1 when x < −2. In fact, the graph of y = |x + 2|/(x + 2)
is the same as the graph of y = |x|/x shifted to the left by 2 units:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(x)
y = csc(x)
y = cot(x)
y = f (x)
−1
1
2
y = g(x)
3
y = h(x)
4
5
−2
f(x) =
1
x
g(x) =
1
x
2
etc.
0
1
π
1
2π
1
3π
1
4π
1
5π
1
6π
1
7π
g(x) = sin
1
x
1
0
−1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
This means that the left-hand limit that we’re looking for is equal to −1 (and
the right-hand limit is 1, and the two-sided limit does not exist).


C h a p t e r 5
Continuity and Differentiability
In general, there’s only one special thing about the graph of a function: it just
has to obey the vertical line test. That’s not particularly exclusive. The graph
could be all over the place—a little bit here, a vertical asymptote there, or
any number of individual disconnected points wherever the hell they feel like
being. So now we’re going to see what happens if we’re a little more exclusive:
we want to look at two types of smoothness. First, continuity: intuitively, this
means that the graph now has to be drawn in one piece, without taking the
pen off the page. Second, differentiability: the intuition here is that there are
no sharp corners in the graph. In both cases, we’ll do a lot better job with
the definition, and we’ll see some of the things you can expect to get from
functions with these special properties. In detail, this is what we’ll look at in
this chapter:
• continuity at a point, and over an interval;
• some examples of continuous functions;
• the Intermediate Value Theorem for continuous functions;
• maxima and minima of continuous functions;
• displacement, average velocity, and instantaneous velocity;
• tangent lines and derivatives;
• second and higher-order derivatives; and
• the relationship between continuity and differentiability.
5.1 Continuity
We’ll start off by looking at what it means for a function to be continuous.
As I said above, the intuition is that you can draw the graph of the function
in one piece, without lifting your pen off the page. This is all very well for
something like y = x
2
, which is all in one piece; but it’s a little unfair for
something like y = 1/x. This would have had a graph in one piece except
for the vertical asymptote at x = 0, which breaks it into two. In fact, if
f(x) = 1/x, then we want to say that f is continuous everywhere except at
