Banner A. The Calculus Lifesaver: All the Tools You Need to Excel at Calculus
Подождите немного. Документ загружается.


96 • Continuity and Differentiability
5.2.11 Differentiability and continuity
Now it’s time to relate the two big concepts in this chapter. I’m going to show
that every differentiable function is also continuous. Another way of looking
at this is that if you know a function is differentiable, you get the continuity
of your function for free. More precisely, I will show:
if a function f is differentiable at x, then it’s continuous at x.
For example, we’ll show in Chapter 7 that sin(x) is differentiable as a function
of x. This will automatically imply that it’s also continuous in x. The same
goes for the other trig functions, exponentials, and logarithms (except at their
vertical asymptotes).
So, how do we prove our big claim? Let’s start by seeing what we want to
prove. To show that f is continuous at x, we’re going to need to show that
lim
u→x
f(u) = f(x),
remembering from Section 5.1.1 above that this equation can only be true
if both sides actually exist! Before we proceed farther, I want to substitute
h = u − x as we’ve done before. In that case, u = x + h, and as u → x, we
see that h → 0. So the above equation can be replaced by
lim
h→0
f(x + h) = f(x).
We need to show that both sides exist and that equality holds—then we’ll be
all done.
Now that we are aware of our destination, let’s start with what we actually
know. Well, we know that f is differentiable at x; this means that f
0
(x) exists,
so by the definition of f
0
, the limit
lim
h→0
f(x + h) − f(x)
h
exists. Let’s first notice that f(x) is involved in this formula, so it must exist
or else the formula is all whacked. So we’ve already gotten somewhere: we
know that f (x) exists. We still need to do something clever. The trick is to
start with another limit:
lim
h→0
f(x + h) − f(x)
h
× h
.
On the one hand, we can work out this limit exactly by splitting it into two
factors:
lim
h→0
f(x + h) − f (x)
h
× h
= lim
h→0
f(x + h) − f (x)
h
× lim
h→0
h = f
0
(x) × 0 = 0.
This works just fine because all the limits involved exist. (That’s where you
need the fact that f
0
(x) exists—otherwise it wouldn’t work.) On the other
hand, we could have taken the original limit and instead canceled out the
factor of h to get
lim
h→0
f(x + h) − f(x)
h
× h
= lim
h→0
(f(x + h) − f (x)).

Section 5.2.11: Differentiability and continuity • 97
Comparing these two previous equations, we just have
lim
h→0
(f(x + h) − f(x)) = 0.
Of course, the value of f(x) doesn’t depend on the limit at all, so we can pull
it out and see that
lim
h→0
f(x + h)
− f(x) = 0.
Now all we have to do is add f(x) to both sides to get
lim
h→0
f(x + h) = f (x)
which is exactly what we wanted! In particular, the limit on the left exists
and equality holds. So we have proved a nice result: differentiable func-
tions are automatically continuous. Remember, though, that continuous
functions aren’t always differentiable!


C h a p t e r 6
How to Solve Differentiation Problems
Now we’ll see how to apply some of the theory from the previous chapter to
solve problems involving differentiation. Finding derivatives from the formula
is possible but cumbersome, so we’ll look at a few rules that make life a lot
easier. All in all, here’s what we’ll tackle in this chapter:
• finding derivatives using the definition;
• using the product, quotient, and chain rules;
• finding equations of tangent lines;
• velocity and acceleration;
• finding limits which are derivatives in disguise;
• how to differentiate piecewise-defined functions; and
• using the graph of a function to draw the graph of its derivative.
6.1 Finding Derivatives Using the Definition
Let’s say we want to differentiate f(x) = 1/x with respect to x. We know
from the previous chapter that the definition of the derivative is
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
f
0
(x) = lim
h→0
f(x + h) − f(x)
h
,
so in our case we have
f
0
(x) = lim
h→0
1
x + h
−
1
x
h
.
If you just replace h by 0 in the fraction, you end up with the indeterminate
form
0
0
. So you need to work a little. In this case, the idea is to simplify the
numerator by taking a common denominator. You get
f
0
(x) = lim
h→0
x − (x + h)
x(x + h)
h
= lim
h→0
−h
hx(x + h)
.
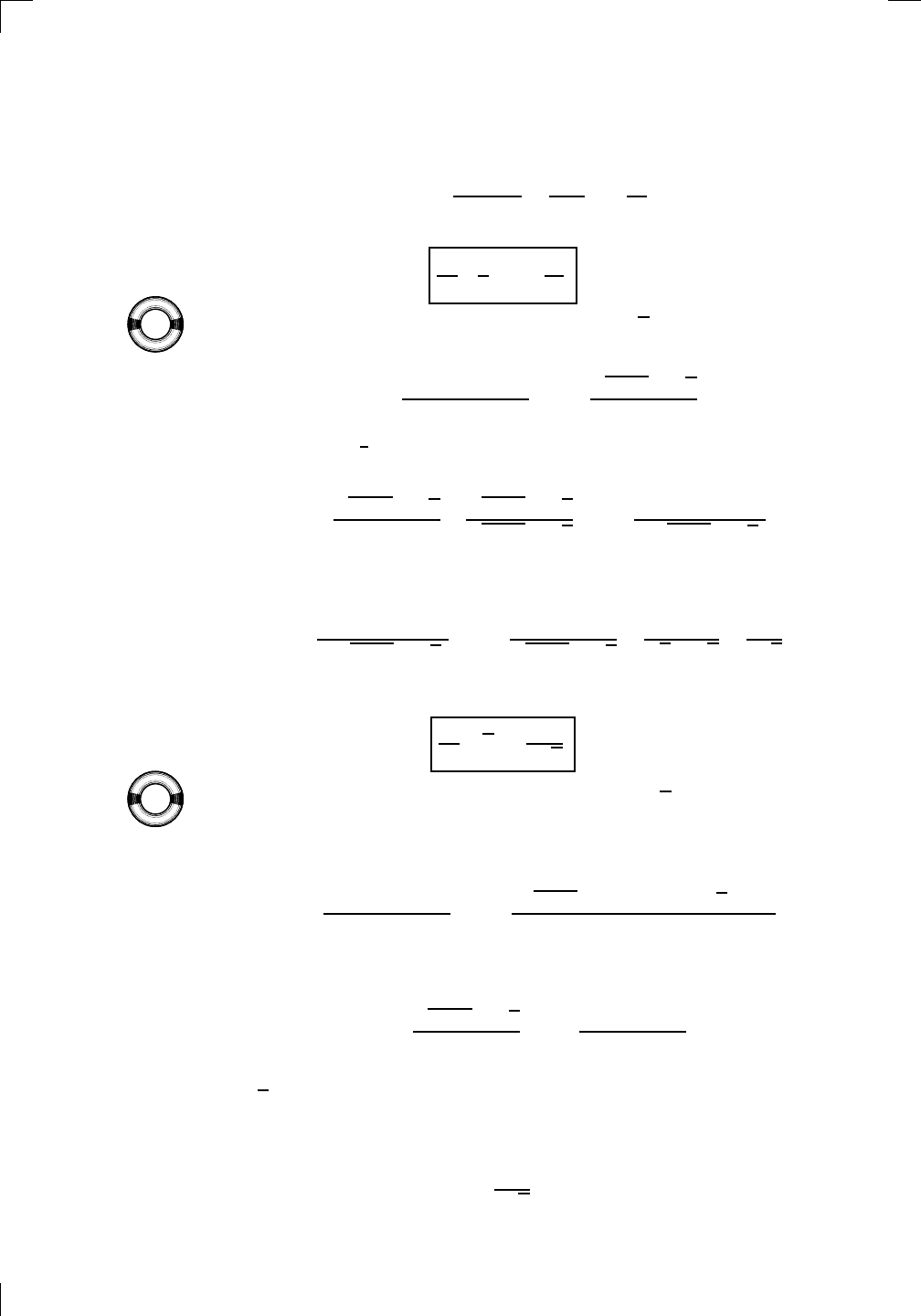
100 • How to Solve Differentiation Problems
Now cancel out a factor of h from top and bottom, then evaluate the limit by
setting h = 0:
f
0
(x) = lim
h→0
−1
x(x + h)
=
−1
x(x)
= −
1
x
2
.
That is,
d
dx
1
x
= −
1
x
2
.
On the other hand, to find the derivative of f(x) =
√
x, you have to employ
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
the trick that we used in Section 4.2 of Chapter 4. Here’s how it goes:
f
0
(x) = lim
h→0
f(x + h) − f(x)
h
= lim
h→0
√
x + h −
√
x
h
,
and we are again in
0
0
territory. Let’s multiply top and bottom by the conju-
gate of the numerator to get
f
0
(x) = lim
h→0
√
x + h −
√
x
h
×
√
x + h +
√
x
√
x + h +
√
x
= lim
h→0
(x + h) − x
h(
√
x + h +
√
x)
;
now we can cancel the x terms on the top, cancel a factor of h from top and
bottom, and take the limit to see that
f
0
(x) = lim
h→0
h
h(
√
x + h +
√
x)
= lim
h→0
1
√
x + h +
√
x
=
1
√
x +
√
x
=
1
2
√
x
.
In summary, we have shown that
d
dx
(
√
x) =
1
2
√
x
.
Now how would you find the derivative of f(x) =
√
x + x
2
using the
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
definition of the derivative? Even if you can just write down the answer,
I’ve asked you to use the definition, so you must put all temptations aside
and use the formula:
f
0
(x) = lim
h→0
f(x + h) − f(x)
h
= lim
h→0
(
√
x + h + (x + h)
2
) − (
√
x + x
2
)
h
.
This looks pretty messy, but if we split it up into the terms involving the
square-root stuff and the terms involving the square stuff, we see that
f
0
(x) = lim
h→0
√
x + h −
√
x
h
+ lim
h→0
(x + h)
2
− x
2
h
.
We know how to do both of these limits; we have just seen that the first one
is 1/2
√
x, and we did the second one in Section 5.2.6 of the previous chapter
and got the answer 2x. You should try doing both of them without looking
back at the previous work and make sure you get the answer
f
0
(x) =
1
2
√
x
+ 2x.

Section 6.1: Finding Derivatives Using the Definition • 101
It’s now time to find the derivative of x
n
with respect to x, where n is
some positive integer. Set f(x) = x
n
; then we have
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
f
0
(x) = lim
h→0
f(x + h) − f (x)
h
= lim
h→0
(x + h)
n
− x
n
h
.
Somehow we have to deal with (x + h)
n
. There are several ways of doing this;
let’s try the most direct approach, which is to write
(x + h)
n
= (x + h)(x + h) ···(x + h).
There are n factors in the above product. This would be a real mess to
multiply out, but it turns out we don’t need to do the whole thing—we just
need to get started. If you take the term x from each factor, there are n of
them, so you get one term x
n
in the product. That’s the only way to get all
x factors, so we already have
(x + h)
n
= (x + h)(x + h) ···(x + h) = x
n
+ stuff involving h.
We need to do a little more work, though. What if you take the term h from
the first factor and x from the others? Then you have one h and (n−1) copies
of x, so you get hx
n−1
when you multiply them all together. There are other
ways to choose one h and the rest x—you could take the h from the second
factor and all others x, or the h from the third factor, and so on. In fact,
there are n ways you could pick one h and the rest x, so you actually have
n copies of hx
n−1
. Together, this makes nhx
n−1
. Every other term in the
expansion has at least two copies of h, so every other term has a factor of h
2
.
All in all, we can write
(x+h)
n
= (x+h)(x+h) ···(x +h) = x
n
+nhx
n−1
+stuff with h
2
as a factor.
Let’s tidy this up one little bit: we’ll write the “stuff with h
2
as a factor” in
the form h
2
× (junk), where “junk” is just a polynomial in x and h. That is,
(x + h)
n
= (x + h)(x + h) ···(x + h) = x
n
+ nhx
n−1
+ h
2
× (junk).
Now we can substitute into the formula for the derivative:
f
0
(x) = lim
h→0
(x + h)
n
− x
n
h
= lim
h→0
x
n
+ nhx
n−1
+ h
2
× (junk) − x
n
h
.
The x
n
terms cancel, and then we can cancel out a factor of h:
f
0
(x) = lim
h→0
nhx
n−1
+ h
2
× (junk)
h
= lim
h→0
(nx
n−1
+ h × (junk)).
As h → 0, the second term goes to 0 (since the junk is pretty benign and
doesn’t blow up!), but the first term remains as nx
n−1
. So we conclude that
d
dx
(x
n
) = nx
n−1
when n is a positive integer. In fact, we’ll show in Section 9.5.1 of Chapter 9
that
d
dx
(x
a
) = ax
a−1
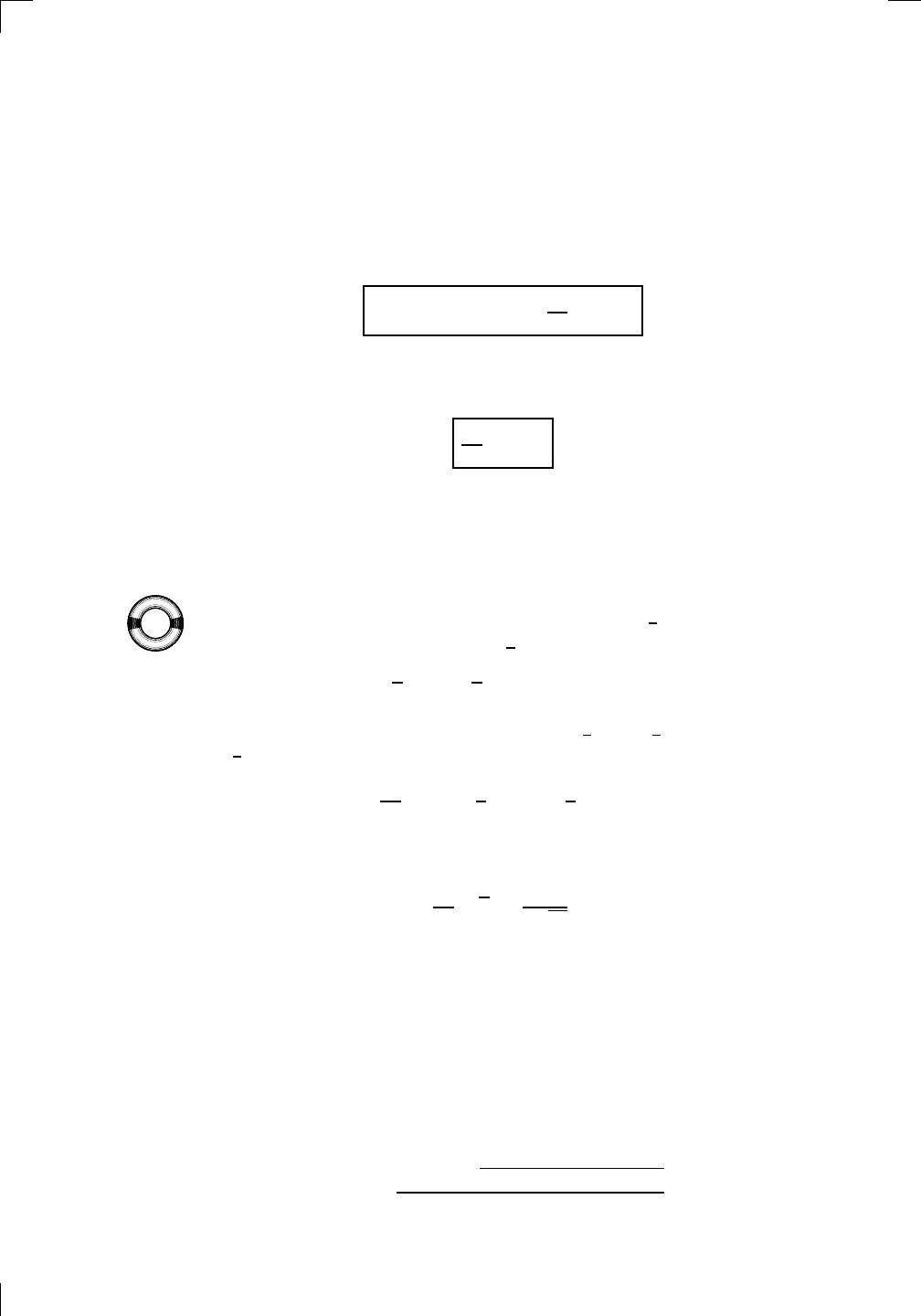
102 • How to Solve Differentiation Problems
when a is any real number at all. In words, you are simply taking the power,
putting a copy of it out front as the coefficient, and then knocking the power
down by 1.
Let’s take a closer look at the above formula. First, when a = 0, then x
a
is the constant function 1. The derivative is then 0x
−1
, which is just 0. This
agrees with the computation we did in Section 5.2.8 of the previous chapter;
in summary,
if C is constant, then
d
dx
(C) = 0.
Now, if a = 1, then x
a
is just x. According to the formula, the derivative
is 1x
0
, which is the constant function 1. Again, this agrees with our results
from Section 5.2.8 of the previous chapter; we have confirmed that
d
dx
(x) = 1.
When a = 2, then we see that the derivative of x
2
with respect to x is 2x
1
,
which is just 2x. This agrees with what we found previously. Similarly, when
a = −1, we can use our formula to see that the derivative of x
−1
is −1 ×x
−2
.
In fact, this just says that the derivative of 1/x is −1/x
2
, which we already
knew from the beginning of this section! This example comes up so often that
you should just learn it individually.
Now let’s try some fractional powers. When a =
1
2
, you see that the
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
derivative with respect to x of x
1/2
is
1
2
x
−1/2
. By the exponential rules (see
Section 9.1.1 in Chapter 9 for a review of these!), you can rewrite this and see
that the derivative of
√
x is 1/2
√
x, which is exactly what we found above.
Again, this comes up so often that it’s worth learning it individually so that
you don’t have to mess around with powers of
1
2
and −
1
2
. Finally, let’s try
a =
1
3
. Our formula says that
d
dx
(x
1/3
) =
1
3
x
1/3−1
=
1
3
x
−2/3
.
Using exponential rules (again, you can find these in Section 9.1.1 of Chap-
ter 9), we can rewrite this whole thing as
d
dx
(
3
√
x) =
1
3
3
√
x
2
.
This one is a little more esoteric, so I wouldn’t worry about learning it. Just
make sure you can derive it using the formula for the derivative of x
a
with
respect to x from the box above.
6.2 Finding Derivatives (the Nice Way)
All this messing about with limits in order to find derivatives is getting a bit
tedious. Luckily, once you do it, you can build up other derivatives from the
ones you’ve already found by means of simple rules. Let’s define a function f
as follows:
f(x) =
3x
7
+ x
4
√
2x
5
+ 15x
4/3
− 23x + 9
6x
2
− 4
.
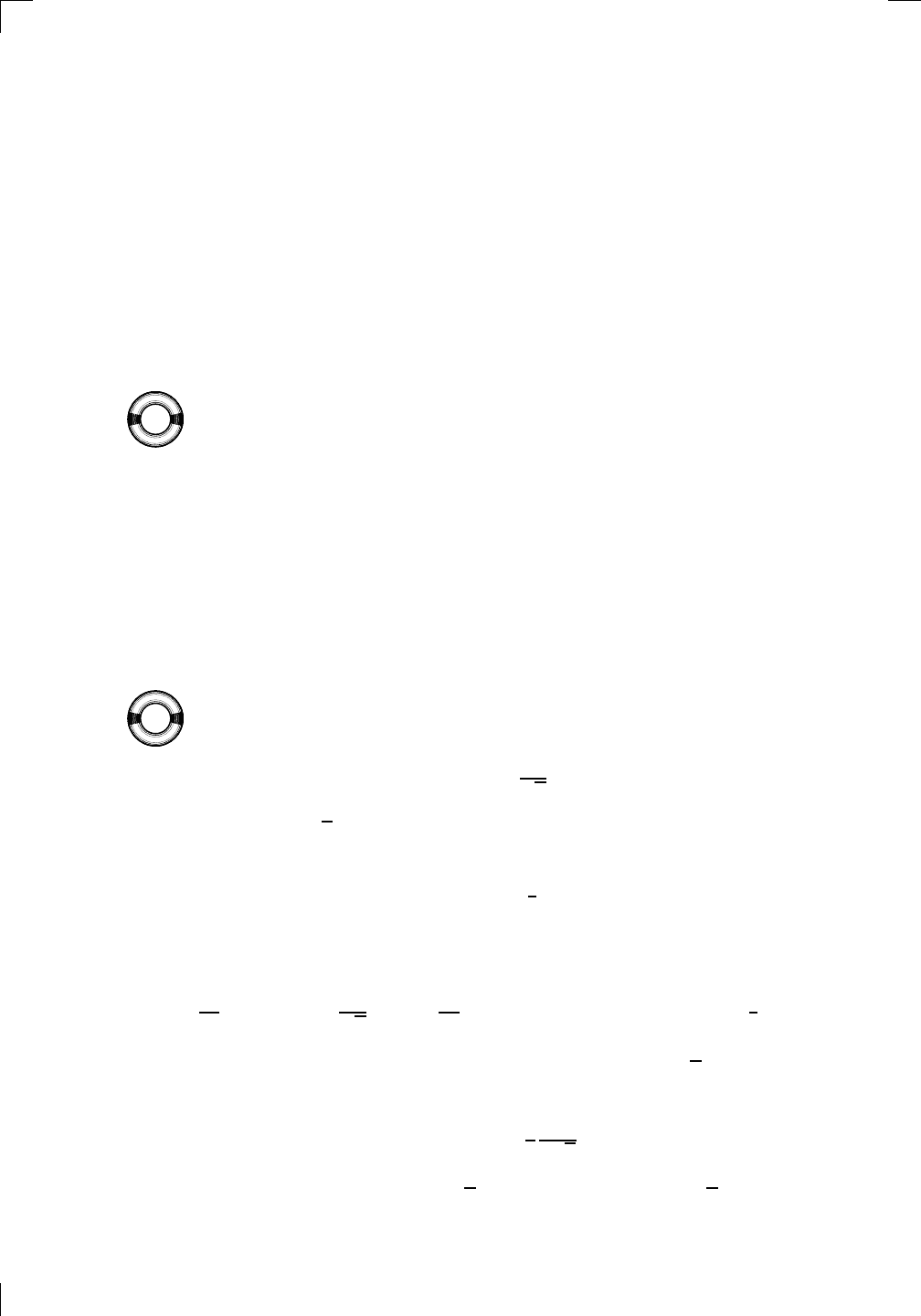
Section 6.2.1: Constant multiples of functions • 103
The key to differentiating a function like this is to understand how it is syn-
thesized from simpler functions. In Section 6.2.6 below, we’ll see how to
use simple operations—multiplication by a constant, adding and subtracting,
multiplying, dividing, and composing functions—to build f from atoms of the
form x
a
, which we already know how to differentiate. First we need to see how
taking derivatives is affected by each of these operations; then we’ll come back
and find f
0
(x) for our nasty function f above. (See Section A.6 of Appendix A
for proofs of the rules below, although there are intuitive justifications of some
of them in Section 6.2.7.)
6.2.1 Constant multiples of functions
It’s easy to deal with a constant multiple of a function: you just multiply by
the constant after you differentiate. For example, we know the derivative of
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
x
2
is 2x; so the derivative of 7x
2
is 7 times 2x, or 14x. The derivative of −x
2
is −2x, since you can think of the minus out front as multiplication by −1.
There’s actually an easy way to take the derivative of a constant multiple of
x
a
. Simply bring the power down, multiply it by the coefficient, and then
knock the power down by one. So for the derivative of 7x
2
, bring the 2 down,
mulitply it by 7 to get the coefficient 14, then knock the power of x down by
one to get 14x
1
or just 14x. Similarly, to find the derivative of 13x
4
, multiply
13 by 4, giving a coefficient of 52, and then knock the power down by one to
get 52x
3
.
6.2.2 Sums and differences of functions
It’s even easier to differentiate sums and differences of functions: just differen-
tiate each piece and then add or subtract. For example, what’s the derivative
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
with respect to x of
3x
5
− 2x
2
+
7
√
x
+ 2?
First write 1/
√
x as x
−1/2
, so this means that we really have to differentiate
3x
5
− 2x
2
+ 7x
−1/2
+ 2. Using the method for constant multiples that we
have just seen, the derivative of 3x
5
is 15x
4
; similarly, the derivative of −2x
2
is −4x, and the derivative of 7x
−1/2
is −
7
2
x
−3/2
. Finally, the derivative of 2
is 0, since 2 is a constant. That is, the +2 at the end is irrelevant, as far as
taking derivatives is concerned. So, we can just put the pieces together to see
that
d
dx
3x
5
− 2x
2
+
7
√
x
+ 2
=
d
dx
(3x
5
−2x
2
+7x
−1/2
+2) = 15x
4
−4x−
7
2
x
−3/2
.
By the way, it’s useful to realize that you can write x
3/2
as x
√
x, so you could
also write the above derivative as
15x
4
− 4x −
7
2
1
x
√
x
.
Similarly, x
5/2
is the same as x
2
√
x, and x
7/2
is the same as x
3
√
x, and so on.
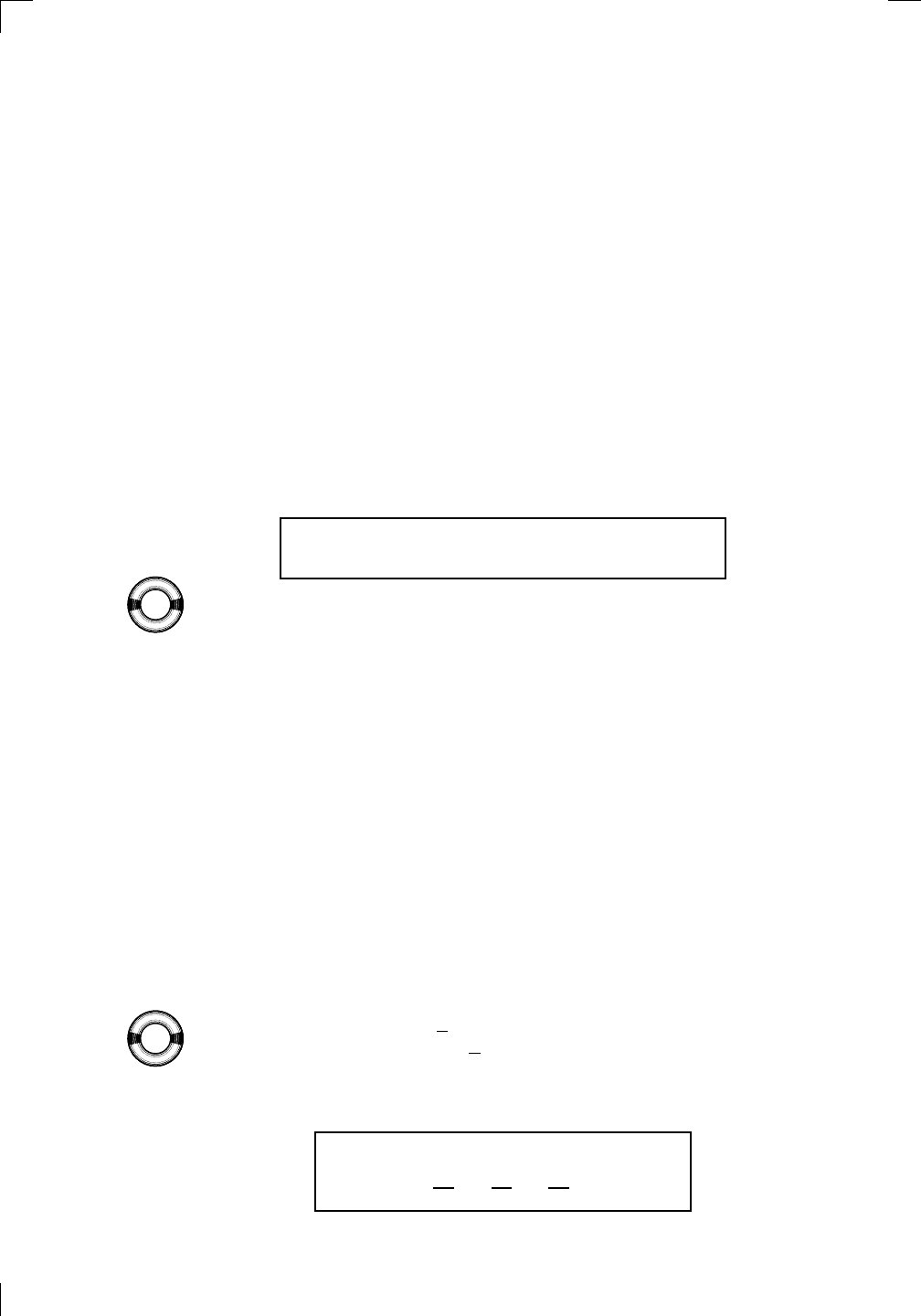
104 • How to Solve Differentiation Problems
6.2.3 Products of functions via the product rule
It’s a little trickier dealing with products—you can’t just multiply the two
derivatives together. For example, let’s say we want to find the derivative of
h(x) = (x
5
+ 2x − 1)(3x
8
− 2x
7
− x
4
− 3x)
without expanding everything first (that would take way too long). Let’s set
f(x) = x
5
+ 2x − 1 and g(x) = 3x
8
− 2x
7
− x
4
− 3x. The function h is the
product of f and g. We can easily write down the derivatives of f and g: they
are f
0
(x) = 5x
4
+ 2 and g
0
(x) = 24x
7
−14x
6
−4x
3
−3. As I said, it’s not true
that the derivative of the product h is the product of these two derivatives.
That is, h
0
(x) 6= (5x
4
+ 2)(24x
7
− 14x
6
− 4x
3
− 3). It’s no good saying what
h
0
(x) isn’t—we need to say what it is!
It turns out that you have to mix and match. That is, you take the
derivative of f and multiply it by g (not the derivative of g). Then you also
have to take the derivative of g and multiply it by f. Finally, add the two
things together. Here’s the rule:
Product rule (version 1): if h(x) = f (x)g(x), then
h
0
(x) = f
0
(x)g(x) + f(x)g
0
(x).
So, for our example of h(x) = (x
5
+ 2x − 1)(3x
8
− 2x
7
− x
4
− 3x), we write
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
h as the product of f and g and then take their derivatives, as we did above.
Let’s summarize what we found, taking a column each for f and g:
f(x) = x
5
+ 2x − 1 g(x) = 3x
8
− 2x
7
− x
4
− 3x
f
0
(x) = 5x
4
+ 2 g
0
(x) = 24x
7
− 14x
6
− 4x
3
− 3.
Now we can use the product rule and do a sort of cross-multiplication. You
see, we need to multiply f
0
(x) on the bottom left by g(x) on the top right,
then add to this the product of f(x) from the top left and g
0
(x) from the
bottom right. So we get
h
0
(x) = f
0
(x)g(x) + f(x)g
0
(x)
= (5x
4
+ 2)(3x
8
− 2x
7
− x
4
− 3x)
+ (x
5
+ 2x − 1)(24x
7
− 14x
6
− 4x
3
− 3).
You could multiply this out, but it would be even worse than multiplying out
the original function h and then differentiating that. Just leave it as it is.
There’s another way to write the product rule. Indeed, sometimes you
have to deal with y = stuff in x, instead of the f(x) form. For example,
suppose y = (x
3
+ 2x)(3x +
√
x + 1). What is dy/dx? In this case, it’s easier
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
to let u = x
3
+ 2x and v = 3x +
√
x + 1. Then we can take the above form of
the product rule and make some replacements: first, u replaces f(x), so that
du/dx replaces f
0
(x); we also do the same thing with v and g(x). We get
Product rule (version 2): if y = uv, then
dy
dx
= v
du
dx
+ u
dv
dx
.
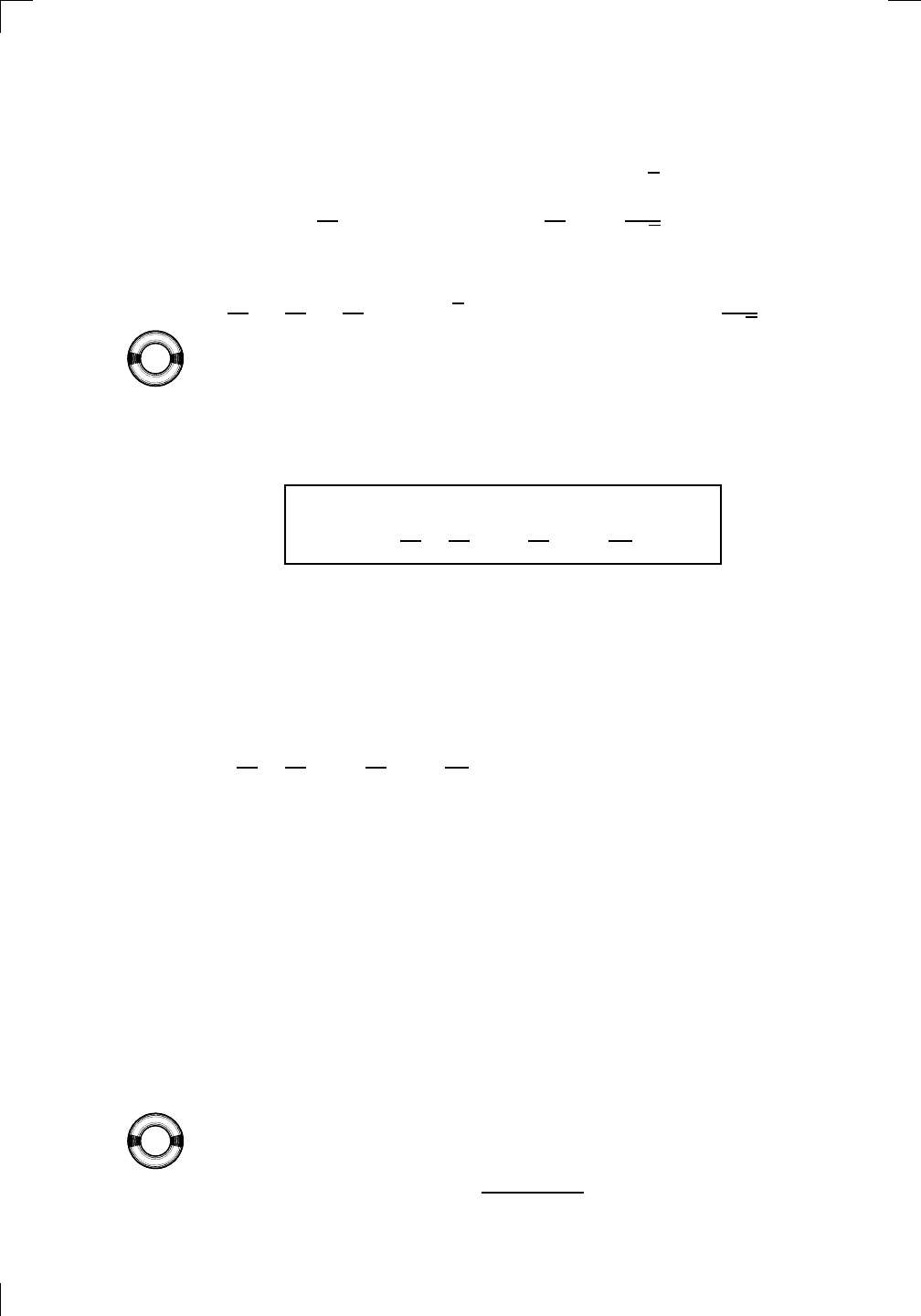
Section 6.2.4: Quotients of functions via the quotient rule • 105
So, in our example, we have
u = x
3
+ 2x v = 3x +
√
x + 1
du
dx
= 3x
2
+ 2
dv
dx
= 3 +
1
2
√
x
.
This means that
dy
dx
= v
du
dx
+ u
dv
dx
= (3x +
√
x + 1)(3x
2
+ 2) + (x
3
+ 2x)
3 +
1
2
√
x
.
What if you have a product of three terms? For example, suppose
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
y = (x
2
+ 1)(x
2
+ 3x)(x
5
+ 2x
4
+ 7)
and you want to find dy/dx. You could multiply it all out and differentiate,
or instead you could use the product rule for three terms:
Product rule (three variables): if y = uvw, then
dy
dx
=
du
dx
vw + u
dv
dx
w + uv
dw
dx
.
Before we finish the example, here’s a tip for remembering the above formula:
just add up uvw three times, but put a d/dx in front of a different variable in
each term. (The same trick works for four or more variables—every variable
gets differentiated once!) Anyway, in our example, we’ll let u = x
2
+ 1,
v = x
2
+ 3x, and w = x
5
+ 2x
4
+ 7, so that y is the product uvw. We have
du/dx = 2x, dv/dx = 2x+3, and dw/dx = 5x
4
+8x
3
. According to the above
formula, we have
dy
dx
=
du
dx
vw + u
dv
dx
w + uv
dw
dx
= (2x)(x
2
+ 3x)(x
5
+ 2x
4
+ 7) + (x
2
+ 1)(2x + 3)(x
5
+ 2x
4
+ 7)
+ (x
2
+ 1)(x
2
+ 3x)(5x
4
+ 8x
3
).
Since we didn’t multiply out and simplify the original expression for y above,
I’m certainly not going to simplify the derivative! I do want to mention,
however, that you can’t always multiply everything out. Sometimes you just
have to use the product rule. For example, after you learn how to differentiate
trig functions in the next chapter, you’ll want to be able to use the product
rule to find derivatives of things like x sin(x). You can’t really multiply this
expression out—it’s already as expanded as it can get. So if you want to
differentiate it with respect to x, there’s no easy way of avoiding using the
product rule.
6.2.4 Quotients of functions via the quotient rule
Quotients are handled in a way similar to products, except that the rule is a
little different. Let’s say you want to differentiate
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−1
(x)
π
2π
y =
sin(x)
x
, x > 3
0
1
−1
a
L
f(x) = x sin (1/x)
(0 < x < 0.3)
h(x) = x
g(x) = −x
a
L
lim
x→a
+
f(x) = L
lim
x→a
+
f(x) = ∞
lim
x→a
+
f(x) = −∞
lim
x→a
+
f(x) DNE
lim
x→a
−
f(x) = L
lim
x→a
−
f(x) = ∞
lim
x→a
−
f(x) = −∞
lim
x→a
−
f(x) DNE
M
}
lim
x→a
−
f(x) = M
lim
x→a
f(x) = L
lim
x→a
f(x) DNE
lim
x→∞
f(x) = L
lim
x→∞
f(x) = ∞
lim
x→∞
f(x) = −∞
lim
x→∞
f(x) DNE
lim
x→−∞
f(x) = L
lim
x→−∞
f(x) = ∞
lim
x→−∞
f(x) = −∞
lim
x→−∞
f(x) DNE
lim
x →a
+
f(x) = ∞
lim
x →a
+
f(x) = −∞
lim
x →a
−
f(x) = ∞
lim
x →a
−
f(x) = −∞
lim
x →a
f(x) = ∞
lim
x →a
f(x) = −∞
lim
x →a
f(x) DNE
y = f (x)
a
y =
|x|
x
1
−1
y =
|x + 2|
x + 2
1
−1
−2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
h(x) =
2x
3
− 3x + 1
x
5
− 8x
3
+ 2
