Banner A. The Calculus Lifesaver: All the Tools You Need to Excel at Calculus
Подождите немного. Документ загружается.


156 • Implicit Differentiation and Related Rates
This simplifies down to
2
d
2
y
dx
2
−
dy
dx
2
=
2
π
.
The problem is, we still need dy/dx! No problem: in our equation
2
dy
dx
+ cos(y)
dy
dx
=
2x
π
from way above, put x = π and y = π/2 (I didn’t let you do this before!) and
you get
2
dy
dx
+ 0
dy
dx
=
2π
π
= 2,
so dy/dx = 1. Put that into our second derivative equation and we get
2
d
2
y
dx
2
− (1)
2
=
2
π
.
This means that
d
2
y
dx
2
=
1
π
+
1
2
when x = π and y = π/2, so we’re finally done!
8.2 Related Rates
Consider two quantities—they can measure anything you like—that are re-
lated to each other. If you know one, you can find the other. For example, if
you keep your eyes on an airplane that passes over your head, then the angle
that your line of sight makes with the ground depends on the position of the
plane. In this case, the two quantities are the position of the plane and the
angle I just described.
Of course, as one of the two quantities changes, so does the other. Suppose
that we know how fast one of the quantities is changing. Then how fast is
the other one changing? That is exactly what we mean by the term related
rates. You see, a rate of change is the speed at which a quantity is changing
over time. We have two quantities which are related to each other, and we
want to know how their rates of change are related to each other. (By the
way, sometimes we’ll abbreviate and say “rate” instead of “rate of change.”)
The above definition of a rate of change was a little sketchy. If you want
to know how fast something is changing over time, you simply have to dif-
ferentiate with respect to time. So, here’s the real definition: the rate of
change of a quantity Q is the derivative of Q with respect to time.
That is,
if Q is some quantity, then the rate of change of Q is
dQ
dt
.
When you see the word “rate,” you should automatically think “d/dt.”
So, how do you go from an equation relating two quantities to an equation
relating the rates of change of these quantities? You differentiate, of course!

Section 8.2.1: A simple example • 157
If you differentiate both sides implicitly with respect to t, you’ll find that
the rates just pop out, giving you a new equation. The same thing works if
you are dealing with three or more quantities which are related (for example,
the length, width, and area of a rectangle). Just differentiate implicitly with
respect to t and you’ll relate the rates of change.
So, let’s look at a general overview of how to solve problems involving
related rates. Then we’ll use it to solve a bunch of examples.
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f (
x)
a
tangen
t at x = a
b
tangen
t at x = b
c
tangen
t at x = c
y = x
2
tangen
t
at x = −
1
u
v
uv
u +
∆u
v +
∆v
(
u + ∆u)(v + ∆v)
∆
u
∆
v
u∆v
v∆u
∆u∆v
y = f (x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
1. Read the question. Identify all the quantities and note which one you
need to find the rate of. Draw a picture if you need to!
2. Write down an equation (sometimes you need more than one) that relates
all the quantities. To do this, you may need to do some geometry,
possibly involving similar triangles. If you have more than one equation,
try to solve them simultaneously to eliminate unnecessary variables.
3. Differentiate your remaining equation(s) implicitly with respect to time
t. That is, whack both sides of each equation with a
d
dt
. You end up
with one or more equations relating the rates of change.
4. Finally, substitute values for everything you know into all the equations
you have. Solve the equations simultaneously to find the rate you need.
The only difference between these types of problems and the word problems
you’ve already seen is that step 3 was absent. Here, it makes all the dif-
ference. Just one more thing before we look at examples: it’s vital that you
substitute values at the end, after differentiating! That is, don’t switch
steps 3 and 4. If you substitute values first, denying the quantities the ability
to change, then your rates will all be 0. That’s what you get for freezing
everything in place. . . .
8.2.1 A simple example
Here’s a relatively simple example to illustrate the above method. Suppose
that a perfectly spherical balloon is being inflated by a pump. Air is entering
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
the balloon at the constant rate of 12π cubic inches per second. At what rate
does the radius of the balloon change at the instant when the radius itself is
2 inches? Also, at what rate does the radius change when the volume is 36π
cubic inches?
OK, let’s write down our quantities (step 1). These are the volume and
the radius of the balloon. Let’s call the volume V (in cubic inches) and the
radius r (in inches). We need to find the rate of change of the radius r. Now,
we need an equation relating V and r (step 2). Here’s where the geometry
comes in. Since the balloon is a sphere, we know that
V =
4
3
πr
3
.
This relates the quantities. Now we need to relate the rates (step 3). Differ-
entiate both sides implicitly with respect to t:
d
dt
(V ) =
d
dt
4
3
πr
3
.

158 • Implicit Differentiation and Related Rates
The left-hand side is just dV /dt; to handle the right-hand side, let s = r
3
, so
ds/dr = 3r
2
. By the chain rule,
ds
dt
=
ds
dr
dr
dt
= 3r
2
dr
dt
.
Now we can put this in our above equation and get
dV
dt
=
4
3
π
3r
2
dr
dt
= 4πr
2
dr
dt
.
So we have an equation relating the rate of V with the rate of r. Finally, we’re
ready to substitute (step 4). In both parts of the question, the rate of change
of volume is 12π cubic inches per second. In symbols, we have dV/dt = 12π.
Plugging this into the above equation, we get
12π = 4πr
2
dr
dt
.
Rearranging leads to
dr
dt
=
3
r
2
.
Great—that means that if we know the radius r, then we can find the rate at
which the radius is changing, which of course is dr/dt. Notice that the rate
of change of the radius is itself a changing quantity: it depends on the radius.
You’ve probably noticed that when you blow up a balloon, it grows in size (or
radius) faster at the beginning, and then starts to slow down, even though
you’re blowing the same amount of air into the balloon all the time. This is
consistent with the above formula for dr/dt, which is decreasing in r.
Armed with the formula, we can quickly do both parts of the question. In
the first part, we know that the radius is 2 inches, so set r = 2 in our formula
from above:
dr
dt
=
3
2
2
=
3
4
.
So the answer is
3
4
. But
3
4
what? It’s important to write a sentence summariz-
ing the situation, as well as including the units of measurement. In this case,
we’d say that when the radius is 2 inches, the rate of change of the radius is
3
4
inches per second.
Now, for the second part of the question, we know that the volume is 36π
cubic inches. That means that V = 36π. The problem is that we need to
know what r is in order to find dr/dt. Now we need to go back to the equation
relating V and r, which was V =
4
3
πr
3
. If you put V = 36π and solve for
r, you should be able to see that r = 3 inches. Finally, substituting into the
equation for dr/dt gives
dr
dt
=
3
r
2
=
3
3
2
=
1
3
.
So when the volume is 36π cubic inches, the rate of change of the radius is
1
3
inches per second.
Section 8.2.2: A slightly harder example • 159
8.2.2 A slightly harder example
Let’s look at another relatively straightforward example, this time involving
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangen
t at x = a
b
tangen
t at x = b
c
tangen
t at x = c
y = x
2
tangen
t
at x = −
1
u
v
uv
u +
∆u
v +
∆v
(
u + ∆u)(v + ∆v)
∆
u
∆
v
u
∆v
v∆
u
∆
u∆v
y = f(
x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
three quantities. Suppose there are two cars, A and B. Car A is driving on a
road heading directly north away from your house, and car B is driving on a
different road heading directly west toward your house. Car A travels at 55
miles per hour and car B travels at 45 miles per hour. At what rate is the
distance between the cars changing when A is 21 miles north of your house
and car B is 28 miles east of your house?
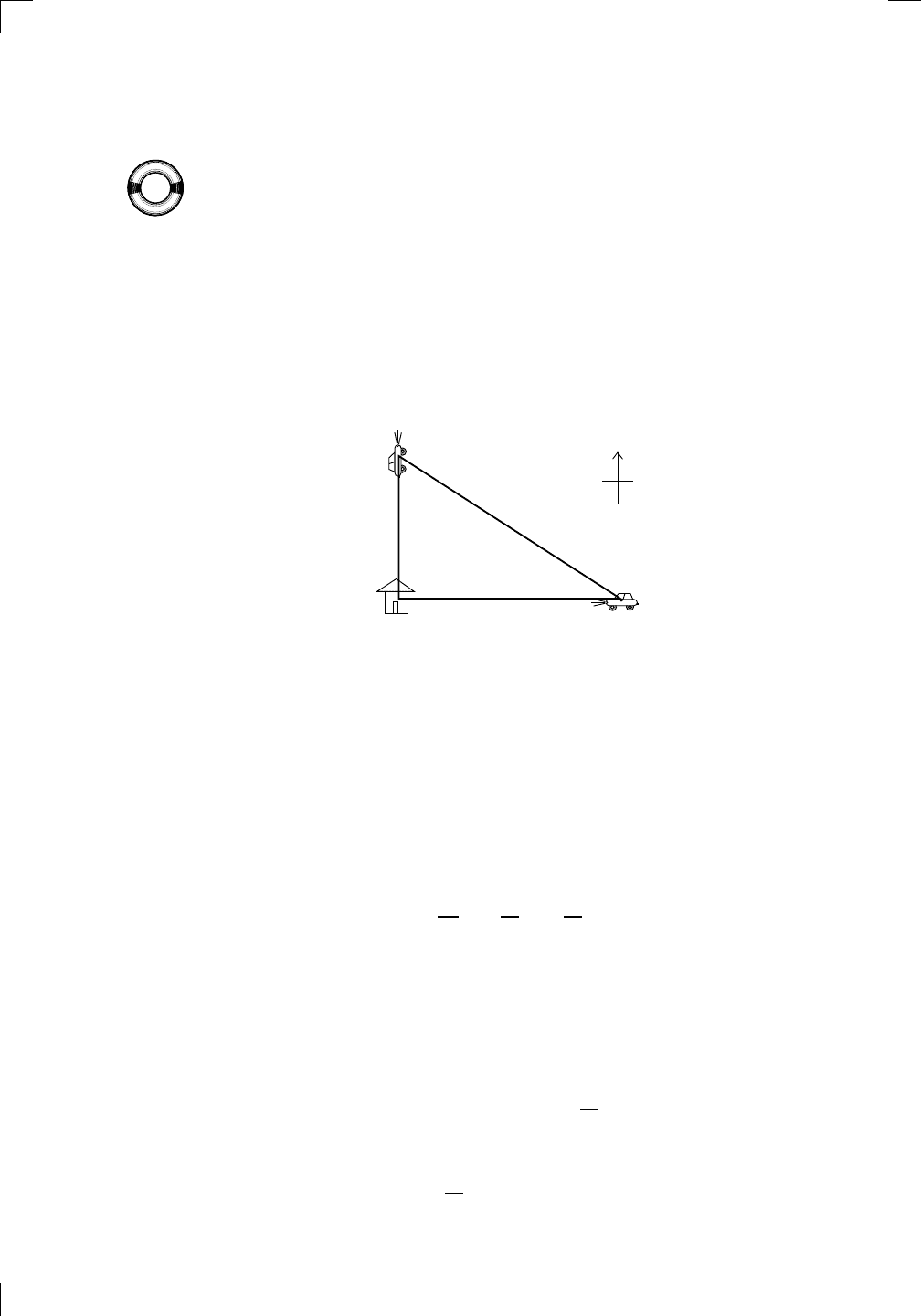
To answer this question, we’d better draw a picture (step 1). Draw your
house H and the cars A and B. Let the distance between H and A be given
by a; let the distance between H and B be called b; and let the distance
between the cars be called c. The diagram looks like this:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f (
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f (
x)
a
tangen
t at x = a
b
tangen
t at x = b
c
tangen
t at x = c
y = x
2
tangen
t
at x = −
1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f (x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
N
A
B
H
a
b
c
Note that it would be wrong to mark in 21 instead of a or 28 instead of b.
You need to see what happens as a and b change, not when they are fixed at
a certain number, so they need to have the flexibility of being variable. Also
note that c is the quantity we need the rate of, since it’s the distance between
the cars.
Time for step 2. The equation relating a, b, and c is nothing other than
Pythagoras’ Theorem:
a
2
+ b
2
= c
2
.
Moving on to step 3, we differentiate implicitly with respect to time t. Make
sure you agree that we get
2a
da
dt
+ 2b
db
dt
= 2c
dc
dt
.
Now, we know that car A is moving at 55 miles an hour away from your
house. This means that the distance a is increasing by 55 miles per hour, so
da/dt = 55. As for B, it is moving at 45 miles an hour toward your house.
This means that b is decreasing by 45 miles an hour, so db/dt = −45. You
need that negative sign in there! Otherwise you’ll screw the whole thing up.
Plugging these values in to the above equation leads to
2a(55) + 2b(−45) = 2c
dc
dt
,
which can be simplified to
c
dc
dt
= 55a − 45b.

160 • Implicit Differentiation and Related Rates
Finally, we can see what happens at the instant of time we’re interested in.
This is when a = 21 and b = 28. At that instant, we know that c
2
= 21
2
+28
2
,
which works out to be c = ±35. Since c is positive (it’s the distance between
the two cars!), we have c = 35. Put those numbers into the above equation
and you get
(35)
dc
dt
= 55(21) − 45(28).
You can compute this easily by canceling a factor of 5 and a factor of 7 from
both sides. The end result is that dc/dt = −3. This means that the distance
between the cars is decreasing at a rate of 3 miles per hour (at the moment
in time we are considering).
That’s the answer we need. Notice that the cars are actually getting closer
together at the moment of time we’re considering, even though A is moving
away from the house faster than B is coming toward it. If we wait a little
bit, car A will be farther away from the house and car B will be closer;
by staring at the equation for dc/dt, you might convince yourself that this
quantity eventually becomes positive (although this observation isn’t required
to complete the question).
8.2.3 A much harder example
Here’s a tougher example involving similar triangles: suppose there’s a freakin’
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangen
t at x = a
b
tangen
t at x = b
c
tangen
t at x = c
y = x
2
tangen
t
at x = −
1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
N
A
B
H
a
b
c
huge water tank in the shape of a cone (with the point at the bottom). The
height of the cone is twice the radius of the cone. Water is being pumped into
the tank at the rate of 8π cubic feet per second. At what rate is the water
level changing when the volume of water in the tank is 18π cubic feet?
There’s a second part as well: assume that the tank develops a little hole
at the bottom that causes water to flow out at a rate of one cubic foot per
second for every cubic foot of water in the tank. I want to know the same
thing as before: at what rate is the water level changing when the volume of
water in the tank is 18π cubic feet, but now with the leak in the tank?
Let’s start with the first part. Here’s a diagram of the situation:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f(
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −x
a
b
c
d
C
a
b
c
d
−1
0
1
2
3
time
y
t
u
(t, f(t))
(u, f(u))
time
y
t
u
y
x
(x, f(x))
y = |x|
(z, f(z))
z
y = f(x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f(x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
N
A
B
H
a
b
c
O
H
A
B
C
D
h
r
R

Section 8.2.3: A much harder example • 161
We have marked some quantities on the diagram. The height of the tank is H
and its radius is R. The height of the water level is h and the radius of the top
of the water surface is r. All these quantities are measured in feet. Let’s also
let v be the volume of water in the tank, measured in cubic feet. (You could
let V be the volume of the whole tank, but we’ll never need that quantity
since the tank will never be full—it’s that huge!). Anyway, that takes care of
step 1.
For step 2, we have to start relating some of these quantities. We are
given that the tank’s height is twice the radius, so we have H = 2R. We’re
more interested in relating h and r, though. There are some similar triangles
in the diagram: in fact, ∆ABO is similar to ∆CDO, so H/R = h/r. Since
H = 2R, we have 2R/R = h/r, which means that h = 2r. So the water is
like a mini-copy of the whole tank. Anyway, we still need to find the volume
of water in the tank in terms of h and r. The volume of a cone of height h
units and radius r units is given by v =
1
3
πr
2
h cubic units. It would be nice
to eliminate one of h and r at this point; since we’re more interested in the
water level h than the radius r (read the question and see why!), it makes
sense to eliminate r. Using the equation r = h/2, we have
v =
1
3
πr
2
h =
1
3
π
h
2
2
h =
πh
3
12
, so v =
πh
3
12
.
Now, for step 3, let’s differentiate this with respect to time t. By the chain
rule,
dv
dt
=
π
12
× 3h
2
dh
dt
=
πh
2
4
dh
dt
, so
dv
dt
=
πh
2
4
dh
dt
.
Great—now for step 4, substitute in everything we know into the two equa-
tions above. We know that dv/dt = 8π and we’re interested in what happens
when v = 18π. Substituting, we get
18π =
πh
3
12
and 8π =
πh
2
4
dh
dt
.
The first equation tells us that h
3
= 18 × 12 = 216, so h = 6. That is, when
the water volume is 18π cubic feet, the water level is at 6 feet. Putting that
into the second equation, we get
8π =
π
4
× 6
2
dh
dt
,
which means that dh/dt = 8/9. That is, the water height is increasing at a
rate of 8/9 feet per second at the moment we care about (when the volume is
18π cubic feet).
The second part is almost the same. In fact, the only difference occurs at
step 4. We still want to substitute in v = 18π, which will mean that h = 6
once again. On the other hand, it’s wrong to put dv/dt = 8π, since that
doesn’t take into account the leak. We know that 8π cubic feet of water is
entering into the tank per second, but one cubic foot is leaving per second for
every cubic foot of water in the tank. Since there are v cubic feet of water in
the tank (by definition!), the rate of outflow from the leak is v cubic feet per
162 • Implicit Differentiation and Related Rates
second. So the rate of inflow is 8π and the rate of outflow is v (both in cubic
feet per second), which means that
dv
dt
= 8π − v.
Now, when v = 18π, we have dv/dt = 8π − 18π = −10π. So we need to
substitute dv/dt = −10π and h = 6 into our previous equation
dv
dt
=
πh
2
4
dh
dt
.
The answer works out to be dh/dt = −10/9, which means that the water
level in the tank is falling at a rate of 10/9 feet per second at the time we’re
considering. Even though we’re pumping water in, the leak is letting even
more water out and so the level is falling.
8.2.4 A really hard example
Here’s one more problem. Now that you have seen a number of related rate
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangen
t at x = a
b
tangen
t at x = b
c
tangen
t at x = c
y = x
2
tangen
t
at x = −
1
u
v
uv
u +
∆u
v +
∆v
(
u + ∆u)(v + ∆v)
∆
u
∆
v
u
∆v
v∆
u
∆
u∆v
y = f(
x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
N
A
B
H
a
b
c
O
H
A
B
C
D
h
r
R
problems, perhaps you should try to solve it before reading the solution.
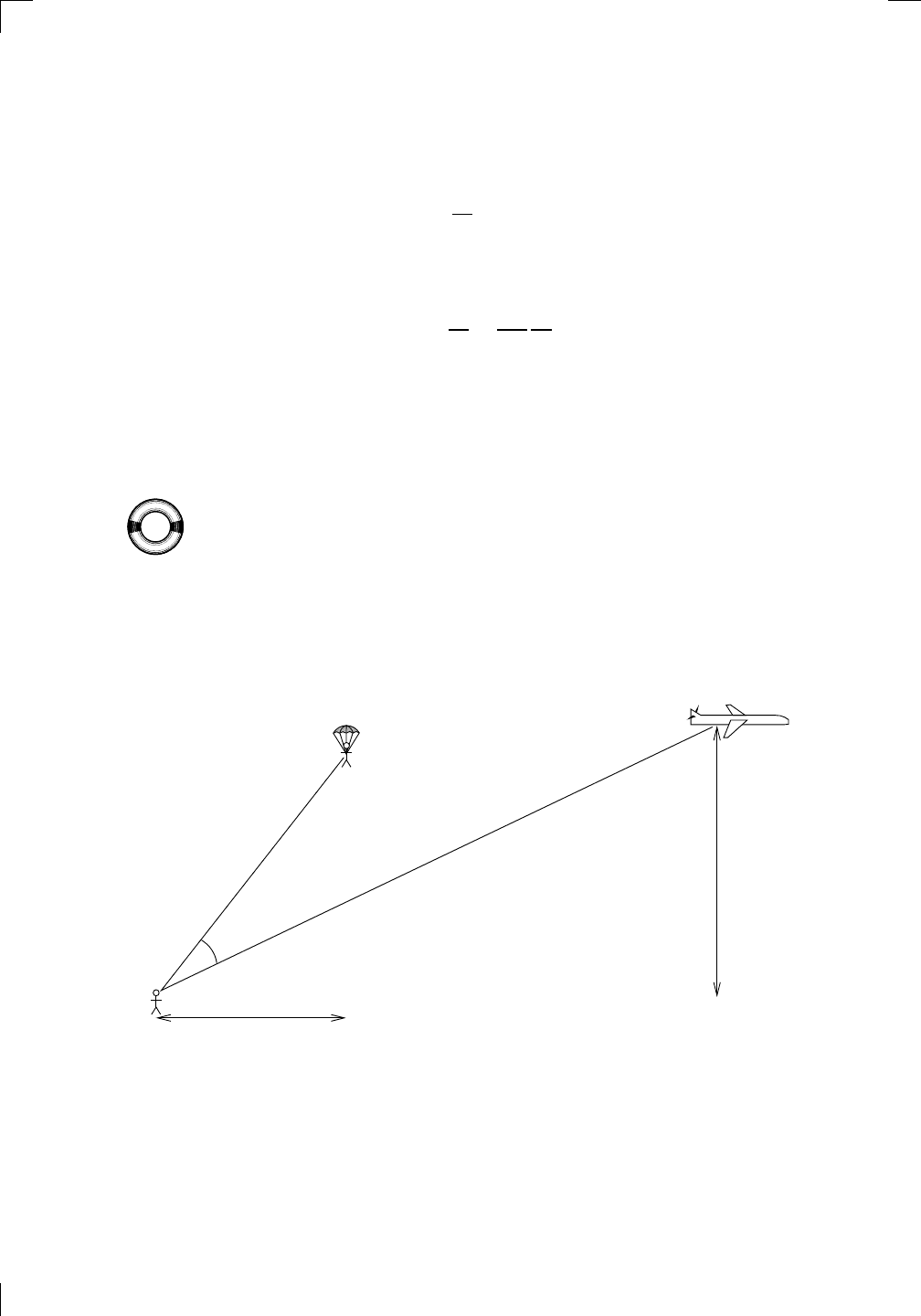
Suppose that a plane is flying eastward directly away from you at a height
of 2000 feet above your head. The plane moves at a constant speed of 500
feet per second. Meanwhile, some time ago a parachutist jumped out of a
helicopter (which has since flown away). The parachutist is floating directly
downward, 1000 feet due east of you, at a constant speed of 10 feet per second.
The situation is summarized in the following picture:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangen
t at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
N
A
B
H
a
b
c
O
H
A
B
C
D
h
r
R
θ
1000
2000
In the picture, what you might call the inter-azimuthal angle between the
parachutist and the plane (with respect to you) is marked as θ. The question
is, at what rate is θ changing when the plane and the parachutist have the
same height but the plane is 8000 feet due east of you?
We have two objects to worry about, the plane and the parachutist. We
know that the height of the plane is always 2000 feet (relative to your head),
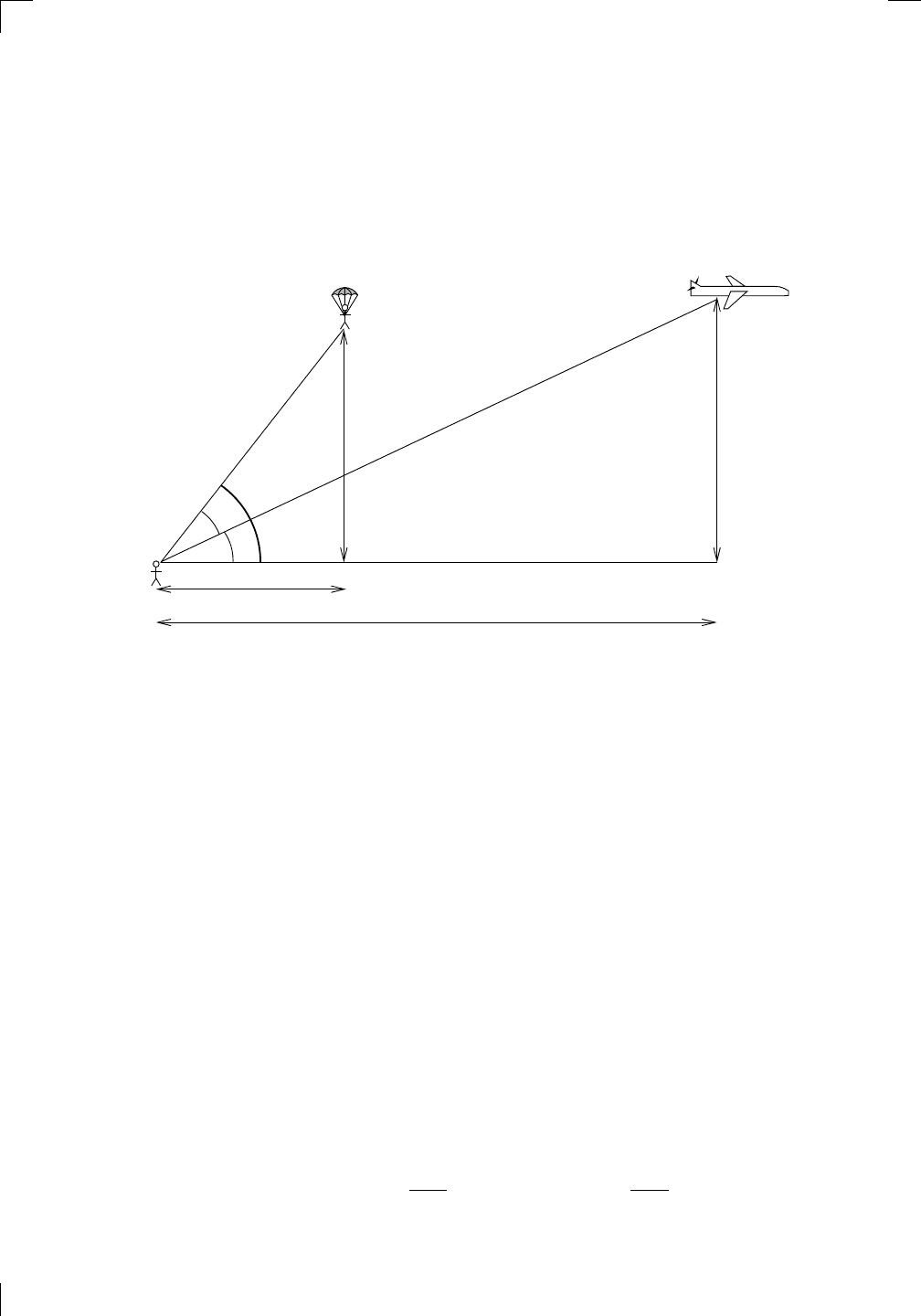
Section 8.2.4: A really hard example • 163
but we don’t know how far east the plane is—the distance keeps on changing.
Let the plane be p feet to the east of you. As for the parachutist, this time
we know exactly how far east the parachutist is: 1000 feet. The problem is,
how high is the parachutist? Let the height be h feet. By drawing a few extra
lines, we can recast the above diagram as follows:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangen
t at x = a
b
tangen
t at x = b
c
tangen
t at x = c
y = x
2
tangen
t
at x = −
1
u
v
uv
u +
∆u
v +
∆v
(
u + ∆u)(v + ∆v)
∆
u
∆
v
u
∆v
v∆
u
∆
u∆v
y = f(
x)
1
2
−
2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
N
A
B
H
a
b
c
O
H
A
B
C
D
h
r
R
θ
1000
2000
α
β
p
h
Notice that the quantities 1000 and 2000 never change, but the quantities p
and h do change. In particular, the plane is heading to the right, so p is getting
bigger; and the parachutist is heading down, so h is getting smaller. Even
though the question asks us to concentrate on the moment when p = 8000
and h = 2000 (the same height as the plane), it’s important that we allow p
and h to vary so that we can work out the rate of change. After all, if p and
h stay the same, then the plane and the parachutist just stay suspended in
space in the same spot, and of course the angle θ wouldn’t change. That’s
hardly realistic—so we need to let p and h vary, in which case θ varies and we
can work out how fast it varies. That completes step 1.
Speaking of θ, it’s clear from the diagram that it is simply the difference
between the angle β the parachutist makes with the ground and the angle α
the plane makes with the ground. (Let’s assume that you have no height, or if
you prefer, you are lying on the ground.) So we know that θ = β−α. Actually,
we should probably write θ = |β − α|, just in case the parachutist is much
lower than the plane. At around the time we’re interested in, the heights are
the same but the plane is much farther to the east than the parachutist, so β
must be bigger than α and we don’t need the absolute values.
Now, let’s do some trig. We have two right-angled triangles. From one of
them (the one with the plane), we get tan(α) = 2000/p. From the other one,
we have tan(β) = h/1000. Let’s write these equations down in one place:
tan(α) =
2000
p
and tan(β) =
h
1000
.

164 • Implicit Differentiation and Related Rates
Step 2 is finally done, and we can move on to step 3, differentiating these
two relations implicitly with respect to time. Starting with the first one, let
u = tan(α) and v = 2000/p, so our equation just becomes u = v. This means
that du/dt = dv/dt. Let’s find these two quantities using the chain rule. First,
du/dt:
du
dt
=
du
dα
dα
dt
= sec
2
(α)
dα
dt
.
And now for dv/dt:
dv
dt
=
dv
dp
dp
dt
= −
2000
p
2
dp
dt
.
Since du/dt = dv/dt, we have
sec
2
(α)
dα
dt
= −
2000
p
2
dp
dt
.
That’s just the first of our two trig equations. We need to repeat the exercise
for the second one involving tan(β). The left-hand side is handled exactly the
same way as we did tan(α), but the right-hand side is much easier. Make sure
you agree that we get
sec
2
(β)
dβ
dt
=
1
1000
dh
dt
.
Remember, we also know that θ = β −α, so we can differentiate this also with
respect to time t and get dθ/dt = dβ/dt − dα/dt. Since there are so many
equations, let’s write all six of them down in one place:
tan(α) =
2000
p
sec
2
(α)
dα
dt
= −
2000
p
2
dp
dt
tan(β) =
h
1000
sec
2
(β)
dβ
dt
=
1
1000
dh
dt
θ = β − α
dθ
dt
=
dβ
dt
−
dα
dt
.
Now we’d better make some substitutions and get to the bottom of this mess.
What do we know? Well, the speed of the plane is 500 feet per second, which
means that dp/dt = 500. The speed of the parachutist is 10 feet per second,
but the height is decreasing, so dh/dt = −10. If you forget the minus sign,
you’ll get the answer wrong! So be very careful. For example, if the plane were
coming toward you, then p would be decreasing, so dp/dt would be negative.
Anyway, we’re interested in what happens when the plane is 8000 feet away,
so p = 8000, and when the parachutist is at height 2000 feet (the same as the
plane), so set h = 2000. The first four of our equations become a lot simpler:
tan(α) =
2000
8000
=
1
4
sec
2
(α)
dα
dt
= −
2000
8000
2
× 500 = −
1
64
tan(β) =
2000
1000
= 2 sec
2
(β)
dβ
dt
=
1
1000
× (−10) = −
1
100
.
From the top right equation, we could find dα/dt if only we knew what sec
2
(α)
was. But wait a second—we do know that tan(α) = 1/4, so surely we can
Section 8.2.4: A really hard example • 165
find sec
2
(α). Remembering our trig identities (see Section 2.4 in Chapter 2),
we get
sec
2
(α) = 1 + tan
2
(α) = 1 +
1
4
2
=
17
16
.
So the top right equation becomes
17
16
dα
dt
= −
1
64
,
which works out to be
dα
dt
= −
1
68
.
This rocks—we now need to do the same with β and we’ll be done. Here we
know that tan(β) = 2, so
sec
2
(β) = 1 + tan
2
(β) = 1 + 2
2
= 5.
Substituting into the bottom right equation above, we have
5
dβ
dt
= −
1
100
,
which means that
dβ
dt
= −
1
500
.
So we know dα/dt and dβ/dt; from the final one of our original six equations
above,
dθ
dt
=
dβ
dt
−
dα
dt
=
−
1
500
−
−
1
68
=
−17 + 125
8500
=
27
2125
.
So the angle θ is increasing at a rate of 27/2125 radians per second (at the
moment we’re considering), and we’re finally done.
