Banner A. The Calculus Lifesaver: All the Tools You Need to Excel at Calculus
Подождите немного. Документ загружается.



C h a p t e r 9
Exponentials and Logarithms
Here’s a big old chapter on exponentials and logarithms. After we review
the properties of these functions, we need to do some calculus with them. It
turns out that there’s a special base, the number e, that works out particularly
nicely. In particular, doing calculus with e
x
and log
e
(x) is a little easier than
dealing with 2
x
or log
3
(x), for example. So we need to spend some time
looking at e. There are other things we want to look at as well; all in all, the
plan is to check out the following topics:
• review of the basics of exponentials and logs, and how they are related
to each other;
• the definition and properties of e;
• how to differentiate exponentials and logs;
• how to solve limit problems involving exponentials and logs;
• logarithmic differentiation;
• exponential growth and decay; and
• hyperbolic functions.
9.1 The Basics
Before you start doing calculus with exponentials and logarithms, you really
need to understand their properties. Basically, in addition to the actual def-
inition of logs, you need to know three things: the exponential rules, the
relationship between logs and exponentials, and the log rules.
9.1.1 Review of exponentials
The rough idea is that we’ll take a positive number, called the base, and raise
it to a power called the exponent:
base
exponent
.
For example, the number 2
−5/2
is an exponential with base 2 and exponent
−5/2. It’s essential that you know the so-called exponential rules, which
168 • Exponentials and Logarithms
effectively tell you how exponentials work. You’ve seen these before, no doubt,
but here they are again to remind you. For any base b > 0 and real numbers
x and y:
1. b
0
= 1. The zeroth power of any nonzero number is 1.
2. b
1
= b. The first power of a number is just the number itself.
3. b
x
b
y
= b
x+y
. When you multiply two exponentials with the same base,
you add the exponents.
4.
b
x
b
y
= b
x−y
. When you divide two exponentials with the same base,
you subtract the bottom exponent from the top one.
5. (b
x
)
y
= b
xy
. When you take the exponential of the exponential, you
multiply the exponents.
You should also know what the graphs of exponentials look like. We looked
at this a little in Section 1.6 in Chapter 1, but in any case we’ll revisit the
graph shortly.
9.1.2 Review of logarithms
Logarithms—a word that strikes fear into the hearts of many students. Watch
carefully, and we’ll see how to deal with these beasts. Suppose that you want
to solve the following equation for x:
2
x
= 7.
The way you can bring x down from the exponent is to hit both sides with a
logarithm. Since the base on the left-hand side is 2, the base of the logarithm
is 2. Indeed, by definition, the solution of the above equation is
x = log
2
(7).
In other words, to what power do you have to raise 2 in order to get 7? The
answer is log
2
(7). This particular number can’t be simplified, but how about
log
2
(8)? Ask yourself, to what power do you raise the base 2 in order to get
8? Since 2
3
= 8, the power we need is 3. So log
2
(8) = 3.
Let’s go back to the equation 2
x
= 7. We know that this means that
x = log
2
(7). If we now plug that value of x into the original equation, we get
the bizarre looking formula
2
log
2
(7)
= 7.
In more generality, log
b
(y) is the power you have to raise the base b
to in order to get y . This means that x = log
b
(y) is the solution of the
equation b
x
= y for given b and y. Plugging this value of y in, we get the
formula
b
log
b
(y)
= y
which is true for any y > 0 and b > 0 (except b = 1). Hey, why do I insist
that b and y be positive? First, if b is negative, then many weird things can
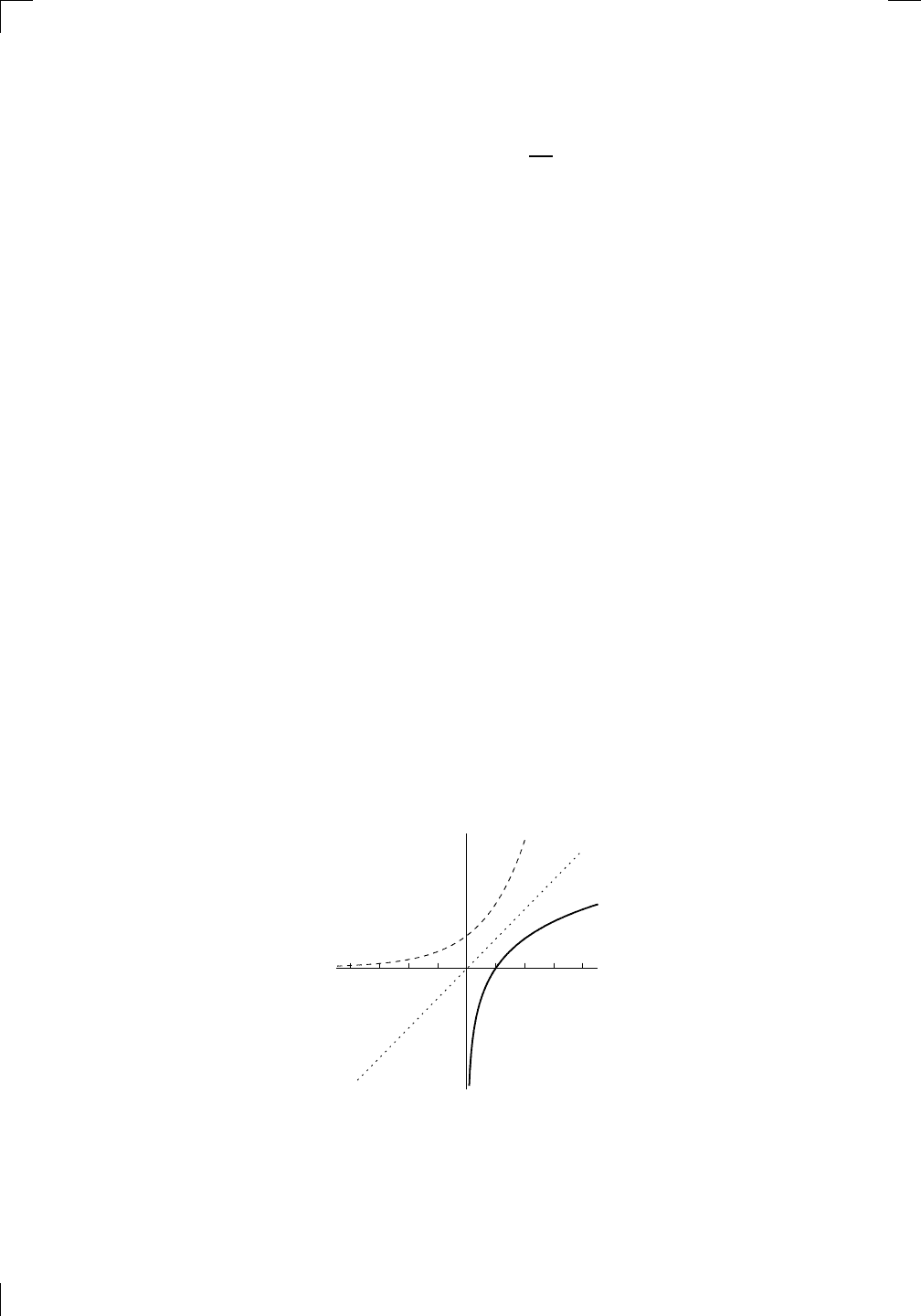
Section 9.1.3: Logarithms, exponentials, and inverses • 169
happen. The quantity b
x
may not be defined. For example, if b = −1 and
x = 1/2, then b
x
is (−1)
1/2
, which is
√
−1 (urk). So we avoid all this by
requiring b > 0. Then there’s no problem taking any power b
x
. On the other
hand, b
x
is always positive! So if y = b
x
then y > 0 by necessity. This means
that it’s nonsense to take the log of a negative number or 0. After all, if
log
b
(y) is the power that you raise b to in order to get y, and you can’t ever
raise b to a power and get a negative number or 0, then y can’t be negative
or 0. You can only take the logarithm of a positive number.
You might also have noticed that I mentioned that b = 1 is bad. If you put
b = 1 in the formula b
log
b
(y)
= y from above, you get 1
log
1
(y)
= y. The problem
is, 1 raised to any power still equals 1, but y may not be 1, so the equation
doesn’t make sense. There just isn’t any base 1 logarithm. How about base
1/2? That’s OK, but there’s rarely any need for a base 1/2 logarithm, since
it turns out that log
1/2
(y) = −log
2
(y) for any number y. (You can prove this
by setting y = (1/2)
x
and noting that y also equals 2
−x
.) The same sort of
thing is true for any base b between 0 and 1: log
b
(y) = −log
1/b
(y) for all y,
and 1/b is greater than 1. So from now on, we’ll always assume that our base
b is greater than 1.
9.1.3 Logarithms, exponentials, and inverses
We can describe everything we’ve seen above in a more sophisticated manner
by using inverse functions. Fix a base b > 1 and set f(x) = b
x
. The function
f has domain R and range (0, ∞). Since it satisfies the horizontal line test, it
has an inverse, which we’ll call g. The domain of g is the range of f, which
is (0, ∞), while the range of g is the domain of f , which is R. We say that g
is the logarithm of base b; in fact, g(x) = log
b
(x) by definition. Remembering
that the graph of the inverse function is the reflection of the original function
in the mirror line y = x, we can draw the graphs of f(x) = b
x
and its inverse
g(x) = log
b
(x) on the same axes:
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f(
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangen
t at x = a
b
tangen
t at x = b
c
tangen
t at x = c
y = x
2
tangent
at x = −1
u
v
uv
u + ∆u
v + ∆v
(u + ∆u)(v + ∆v)
∆u
∆v
u∆v
v∆u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f(x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
N
A
B
H
a
b
c
O
H
A
B
C
D
h
r
R
θ
1000
2000
α
β
p
h
y = g(x) = log
b
(x)
y = f(x) = b
x
Since f and g are inverses of each other, we know that f(g(x)) = x and
g(f(x)) = x. (The first fact is only true for x > 0, as we will see.) Let’s
interpret these two facts, one at a time.
170 • Exponentials and Logarithms
1. We’ll start off with f(g(x)) = x. Since g is the logarithm function, x
had better be positive—remember, you can only take the log of a positive
number. Now let’s take a close look at the quantity f(g(x)). You start out
with a positive number x, and hit it with g, which is the base b logarithm. You
then exponentiate the result: that is, you raise b to the power of g(x). You end
up with your original number! In fact, since f(x) = b
x
and g(x) = log
b
(x),
the formula f(g(x)) = x just says that
b
log
b
(x)
= x,
which was one of our formulas from the previous section (with y replaced
by x). The exponential of the logarithm is the original number—
provided that the bases match!
2. Our other fact is that g(f(x)) = x, which is true for all x. Now we take
a number x, raise b to the power of our number x, then take the base b
logarithm. Once again, we get the original number x back. It’s sort of like
taking a positive number, squaring it and then taking the square root: you get
the original number back. Since f(x) = b
x
and g(x) = log
b
(x), the equation
g(f(x)) = x becomes
log
b
(b
x
) = x for any real x and b > 1.
For example, when we looked at the equation 2
x
= 7 in the previous section,
you can take log
2
of both sides to get
log
2
(2
x
) = log
2
(7).
The left-hand side is just x, because the logarithm of the exponential
is the original number (provided that the bases match!). One more quick
example: to solve
PSfrag
replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shado
w
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror
(y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y =
(x − 1)
2
−
1
x
Same
height
−
x
Same
length,
opp
osite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y =
2
x
y =
10
x
y =
2
−x
y =
log
2
(x)
4
3
units
mirror
(x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
=
0 radians
θ
hypotenuse
opp
osite
adjacen
t
0
(≡ 2π)
π
2
π
3
π
2
I
I
I
I
II
IV
θ
(
x, y)
x
y
r
7
π
6
reference
angle
reference
angle =
π
6
sin
+
sin −
cos
+
cos −
tan
+
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this
angle is
5π
6
clo
ckwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y =
sin(x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y =
sin(x)
y =
cos(x)
−
π
2
π
2
y =
tan(x), −
π
2
<
x <
π
2
0
−
π
2
π
2
y =
tan(x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y =
sec(x)
y =
csc(x)
y =
cot(x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y =
tan
−1
(x)
π
2
π
y =
sin(
x)
x
,
x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 <
x < 0.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x +
2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangen
t at x = a
b
tangen
t at x = b
c
tangen
t at x = c
y = x
2
tangen
t
at x = −
1
u
v
uv
u +
∆u
v +
∆v
(
u + ∆u)(v + ∆v)
∆
u
∆
v
u
∆v
v∆
u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
N
A
B
H
a
b
c
O
H
A
B
C
D
h
r
R
θ
1000
2000
α
β
p
h
y = g(x) = log
b
(x)
y = f(x) = b
x
3
x
2
−1
= 19,
simply take log
3
of both sides:
log
3
3
x
2
−1
= log
3
(19).
The left-hand side is just x
2
− 1, so we have x
2
− 1 = log
3
(19). This means
that x = ±
p
log
3
(19) + 1.
9.1.4 Log rules
The exponential rules from Section 9.1.1 above all have log versions, which are
(strangely enough) called log rules. There’s actually an extra log rule—the
change of base rule—that doesn’t have a corresponding exponential rule (see
#6 below).
∗
So, here are the rules, which are valid for any base b > 1 and
positive real numbers x and y:
∗
Actually, there is a change of base rule for exponentials too: b
x
= c
x log
c
(b)
for b > 0,
c > 1, and x > 0. This isn’t normally included in the list of exponential rules because it
involves logarithms!

Section 9.1.4: Log rules • 171
1. log
b
(1) = 0.
2. log
b
(b) = 1.
3. log
b
(xy) = log
b
(x) + log
b
(y). The log of the product is the
sum of the logs.
4. log
b
(x/y) = log
b
(x) − log
b
(y). The log of the quotient is the
difference of the logs.
5. log
b
(x
y
) = y log
b
(x).
The log moves the exponent down in front
of the log. In this equation, y can be any real
number (positive, negative or zero).
6. Change of base rule:
log
b
(x) =
log
c
(x)
log
c
(b)
for any bases b > 1 and c > 1 and any number x > 0. This means that
all the log functions with different bases are really constant multiples of
each other. Indeed, the above equation says that
log
b
(x) = K log
c
(x),
where K is constant (it happens to be equal to 1/ log
c
(b)). When I say
“constant,” I mean it doesn’t depend on x. We can conclude that the
graphs of y = log
b
(x) and y = log
c
(x) are very similar—you just stretch
the second one vertically by a factor of K to get the first one.
Now, let’s see why these rules are all true. If you want, you can skip to the
next section, but believe me, you’ll understand logs a whole lot better if you
read on. Anyway, #1 above is pretty easy: because b
0
= 1 for any base b > 1,
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x + 2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −
1
u
v
uv
u + ∆
u
v + ∆
v
(
u + ∆u)(v + ∆v)
∆
u
∆
v
u
∆v
v∆
u
∆u∆v
y = f(x)
1
2
−2
y = |x
2
− 4|
y = x
2
− 4
y = −2x + 5
y = g(x)
1
2
3
4
5
6
7
8
9
0
−1
−2
−3
−4
−5
−6
y = f (x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
N
A
B
H
a
b
c
O
H
A
B
C
D
h
r
R
θ
1000
2000
α
β
p
h
y = g(x) = log
b
(x)
y = f(x) = b
x
we have log
b
(1) = 0. The same sort of thing works for #2: since b
1
= b for
any b > 1, we can just write down log
b
(b) = 1.
The third rule is harder. We must show that log
b
(xy) = log
b
(x) + log
b
(y),
where x and y are positive and b > 1. Let’s start off with our important fact,
which we’ve noted a couple of times above (with A replacing the previous
variable):
b
log
b
(A)
= A
for any A > 0. If we apply this three times with A replaced by x, y, and xy,
respectively, we get
b
log
b
(x)
= x, b
log
b
(y)
= y, and b
log
b
(xy)
= xy.
Now you can just multiply the first and second of these equations together,
then compare with the third equation to get
b
log
b
(x)
b
log
b
(y)
= xy = b
log
b
(xy)
.
So what? Well, use exponential rule #3 on the left-hand side; since we have
to add the exponents, the equation becomes
b
log
b
(x)+log
b
(y)
= b
log
b
(xy)
.

172 • Exponentials and Logarithms
Now hit both sides with a base b log to kill the base b on both sides; we’re
left with our log rule log
b
(x) + log
b
(y) = log
b
(xy). Not so bad!
As for rule #4 above, I leave it to you to show this; the proof is almost
PSfrag replacements
(
a, b)
[
a, b]
(
a, b]
[
a, b)
(
a, ∞)
[
a, ∞)
(
−∞, b)
(
−∞, b]
(
−∞, ∞)
{
x : a < x < b}
{
x : a ≤ x ≤ b}
{
x : a < x ≤ b}
{
x : a ≤ x < b}
{
x : x ≥ a}
{
x : x > a}
{
x : x ≤ b}
{
x : x < b}
R
a
b
shadow
0
1
4
−
2
3
−
3
g(
x) = x
2
f(
x) = x
3
g(
x) = x
2
f(
x) = x
3
mirror (
y = x)
f
−
1
(x) =
3
√
x
y = h
(x)
y = h
−
1
(x)
y = (
x − 1)
2
−
1
x
Same height
−
x
Same length,
opposite signs
y = −
2x
−
2
1
y =
1
2
x − 1
2
−
1
y = 2
x
y = 10
x
y = 2
−
x
y = log
2
(
x)
4
3 units
mirror (
x-axis)
y = |
x|
y = |
log
2
(x)|
θ radians
θ units
30
◦
=
π
6
45
◦
=
π
4
60
◦
=
π
3
120
◦
=
2
π
3
135
◦
=
3
π
4
150
◦
=
5
π
6
90
◦
=
π
2
180
◦
= π
210
◦
=
7
π
6
225
◦
=
5
π
4
240
◦
=
4
π
3
270
◦
=
3
π
2
300
◦
=
5
π
3
315
◦
=
7
π
4
330
◦
=
11
π
6
0
◦
= 0 radians
θ
hypotenuse
opposite
adjacent
0 (
≡ 2π)
π
2
π
3
π
2
I
II
III
IV
θ
(
x, y)
x
y
r
7
π
6
reference angle
reference angle =
π
6
sin +
sin −
cos +
cos −
tan +
tan −
A
S
T
C
7
π
4
9
π
13
5
π
6
(this angle is
5
π
6
clockwise)
1
2
1
2
3
4
5
6
0
−
1
−
2
−
3
−
4
−
5
−
6
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
π
2
y = sin(
x)
1
0
−
1
−
3π
−
5
π
2
−
2π
−
3
π
2
−
π
−
π
2
3
π
5
π
2
2
π
2
π
3
π
2
π
π
2
y = sin(
x)
y = cos(
x)
−
π
2
π
2
y = tan(
x), −
π
2
< x <
π
2
0
−
π
2
π
2
y = tan(
x)
−
2π
−
3π
−
5
π
2
−
3
π
2
−
π
−
π
2
π
2
3
π
3
π
5
π
2
2
π
3
π
2
π
y = sec(
x)
y = csc(
x)
y = cot(
x)
y = f(
x)
−
1
1
2
y = g(
x)
3
y = h
(x)
4
5
−
2
f(
x) =
1
x
g(
x) =
1
x
2
etc.
0
1
π
1
2
π
1
3
π
1
4
π
1
5
π
1
6
π
1
7
π
g(
x) = sin
1
x
1
0
−
1
L
10
100
200
y =
π
2
y = −
π
2
y = tan
−
1
(x)
π
2
π
y =
sin(
x)
x
, x > 3
0
1
−
1
a
L
f(
x) = x sin (1/x)
(0 < x < 0
.3)
h
(x) = x
g(
x) = −x
a
L
lim
x
→a
+
f(x) = L
lim
x
→a
+
f(x) = ∞
lim
x
→a
+
f(x) = −∞
lim
x
→a
+
f(x) DNE
lim
x
→a
−
f(x) = L
lim
x
→a
−
f(x) = ∞
lim
x
→a
−
f(x) = −∞
lim
x
→a
−
f(x) DNE
M
}
lim
x
→a
−
f(x) = M
lim
x
→a
f(x) = L
lim
x
→a
f(x) DNE
lim
x
→∞
f(x) = L
lim
x
→∞
f(x) = ∞
lim
x
→∞
f(x) = −∞
lim
x
→∞
f(x) DNE
lim
x
→−∞
f(x) = L
lim
x
→−∞
f(x) = ∞
lim
x
→−∞
f(x) = −∞
lim
x
→−∞
f(x) DNE
lim
x →a
+
f(
x) = ∞
lim
x →a
+
f(
x) = −∞
lim
x →a
−
f(
x) = ∞
lim
x →a
−
f(
x) = −∞
lim
x →a
f(
x) = ∞
lim
x →a
f(
x) = −∞
lim
x →a
f(
x) DNE
y = f (
x)
a
y =
|
x|
x
1
−
1
y =
|
x + 2|
x + 2
1
−
1
−
2
1
2
3
4
a
a
b
y = x sin
1
x
y = x
y = −
x
a
b
c
d
C
a
b
c
d
−
1
0
1
2
3
time
y
t
u
(
t, f(t))
(
u, f(u))
time
y
t
u
y
x
(
x, f(x))
y = |
x|
(
z, f(z))
z
y = f(
x)
a
tangent at x = a
b
tangent at x = b
c
tangent at x = c
y = x
2
tangent
at x = −
1
u
v
uv
u + ∆
u
v + ∆
v
(
u + ∆u)(v + ∆v)
∆
u
∆
v
u
∆v
v∆
u
∆
u∆v
y = f(
x)
1
2
−
2
y = |
x
2
− 4|
y = x
2
− 4
y = −
2x + 5
y = g(
x)
1
2
3
4
5
6
7
8
9
0
−
1
−
2
−
3
−
4
−
5
−
6
y = f (
x)
3
−3
3
−3
0
−1
2
easy
hard
flat
y = f
0
(x)
3
−3
0
−1
2
1
−1
y = sin(x)
y = x
x
A
B
O
1
C
D
sin(x)
tan(x)
y =
sin(x)
x
π
2π
1
−1
x = 0
a = 0
x > 0
a > 0
x < 0
a < 0
rest position
+
−
y = x
2
sin
1
x
N
A
B
H
a
b
c
O
H
A
B
C
D
h
r
R
θ
1000
2000
α
β
p
h
y = g(x) = log
b
(x)
y = f(x) = b
x
identical to the one we just did for #3. So, let’s go on to #5. We want to
show that log
b
(x
y
) = y log
b
(x), where x > 0, b > 1, and y is any number at
all. To do this, start with the important fact from above but with A replaced
by x
y
. We get
b
log
b
(x
y
)
= x
y
.
This gives us a weird way of expressing x
y
. We could also replace A instead
by x to get
b
log
b
(x)
= x,
then raise both sides to the power y:
(b
log
b
(x)
)
y
= x
y
.
The left-hand side of this is just b
y log
b
(x)
by exponential rule #5 (see Sec-
tion 9.1.1 above). So we have two different expressions for x
y
, which must be
equal to each other:
b
log
b
(x
y
)
= b
y log
b
(x)
.
Again, hitting both sides with a logarithm base b reduces everything to our
log rule
log
b
(x
y
) = y log
b
(x).
Finally, we just need to prove the change of base rule. We’re actually going
to show that
log
b
(x) log
c
(b) = log
c
(x).
You see, if that’s true, then just divide both sides by log
c
(b) to get the rule as
it’s described in #6 above. Anyway, let’s take the equation above and raise c
to the power the left-hand side and right-hand side separately. We get
c
log
b
(x) log
c
(b)
and c
log
c
(x)
,
respectively. The right-hand side is easy: it’s just x because of our important
fact. How about the left-hand side? We use exponential rule #5 again in a
tricky way to write
c
log
b
(x) log
c
(b)
= c
log
c
(b)×log
b
(x)
=
c
log
c
(b)
log
b
(x)
.
Since c
log
c
(b)
= b and b
log
b
(x)
= x by our important fact (twice), we conclude
that
c
log
b
(x) log
c
(b)
=
c
log
c
(b)
log
b
(x)
= b
log
b
(x)
= x.
So both of the quantities
c
log
b
(x) log
c
(b)
and c
log
c
(x)
from above simplify down to just x! They must be equal to each other, then,
and if we knock out the base of c (using a base c logarithm), we get our desired
equation
log
b
(x) log
c
(b) = log
c
(x).
Well done if you took the trouble to understand all these proofs.

Section 9.2: Definition of e • 173
9.2 Definition of e
So far, we haven’t done any calculus involving exponentials or logs. Let’s start
doing some. We’ll begin with limits and then move on to derivatives. Along
the way, we need to introduce a new constant e, which is a special number in
the same sort of way that π is a special number—it just pops up when you
start exploring math deeply enough. One way of seeing where e comes from
involves a bit of a finance lesson.
9.2.1 A question about compound interest
A long time ago, a dude named Bernoulli answered a question about com-
pound interest. Here’s the setup for his question. Let’s suppose you have a
bank account at a bank that pays interest at a generous rate of 12% annu-
ally, compounded once a year. You put in an initial deposit; every year, your
fortune increases by 12%. This means that after n years, your fortune has
increased by a factor of (1 +0.12)
n
. In particular, after one year, your fortune
is just (1 + 0.12) = 1.12 times the original amount. If you started with $100,
you’d finish the year with $112.
Now suppose you find another bank that also offers an annual interest rate
of 12%, but now it compounds twice a year. Of course you aren’t going to get
12% for half a year; you have to divide that by 2. Basically this means that
you are getting 6% interest for every 6 months. So, if you put money into this
bank account, then after one year it has compounded twice at 6%; the result
is that your fortune has expanded by a factor of (1 + 0.06)
2
, which works out
to be 1.1236. So if you started with $100, you’d finish with $112.36.
The second account is a little better than the first. It makes sense when
you think about it—compounding is beneficial, so compounding more often
at the same annual rate should be better. Let’s try 3 times a year at the
annual rate of 12%. We take 12% and divide by 3 to get 4%, then compound
three times; our fortune has increased by (1 + 0.04)
3
, which works out to be
1.124864. This is a little higher still. How about 4 times a year? That’d be
(1 + 0.03)
4
, which is approximately 1.1255. That’s even higher. Now, the
question is, where does it stop? If you compound more and more often at the
same annual rate, do you get wads and wads of cash after a year, or is there
some limitation on all this?
9.2.2 The answer to our question
To answer our question, let’s turn to some symbols. First, let’s suppose that
we are compounding n times a year at an annual rate of 12%. This means
that each time we compound, the amount of compounding is 0.12/n. After
this happens n times in one year, our original fortune has grown by a factor
of
1 +
0.12
n
n
.
We want to know what happens if we compound more and more often; in
fact, let’s allow n to get larger and larger. That is, we’d like to know what

174 • Exponentials and Logarithms
happens in the limit as n → ∞: what on earth is
lim
n→∞
1 +
0.12
n
n
?
It would also be nice to know what happens at interest rates other than 12%.
So let’s replace 0.12 by r and worry about the more general limit
L = lim
n→∞
1 +
r
n
n
.
If this limit (which I called L) turns out to be infinite, then by compounding
more and more often, you could get more and more money in a single year.
On the other hand, if it turns out to be finite, we’ll have to conclude that
there is a limitation on how much we can increase our fortune with an annual
interest rate of r, no matter how often we compound. There would be a sort
of “speed limit,” or more accurately, a “fortune-increase limit.” Given a fixed
annual interest rate r and one year to play with, you can never increase your
fortune by a factor of more than the value of the above limit (assuming it’s
finite) no matter how often you compound.
The quantity (1 + r/n)
n
which occurs in the limit is a special case of the
formula for compound interest. In general, suppose you start with $A in cash
and you put it in a bank account at an annual interest rate of r, compounded
n times a year. Then over t years, the compounding will occur nt times at
a rate of r/n each time; so your fortune after t years will be given by the
following formula:
fortune after t years, compounded n times a
year at a rate of r per year = A
1 +
r
n
nt
.
So we are just starting with $1 (so A = 1) and seeing what happens after one
year (so t = 1), then seeing what happens in the limit if we compound more
and more times a year.
Now let’s attack our limit:
L = lim
n→∞
1 +
r
n
n
.
First, let’s set h = r/n, so that n = r/h. Then as n → ∞, we see that h → 0
+
(since r is constant), so
L = lim
h→0
+
(1 + h)
r/h
.
Now we can use our exponential rule to write
L = lim
h→0
+
((1 + h)
1/h
)
r
.
Let’s pull a huge rabbit out of the hat and set
e = lim
h→0
+
(1 + h)
1/h
.
Where is the trickery? Well, the limit might not exist. It turns out that it
does; see Section A.5 of Appendix A if you want to know why. In any case, we
Section 9.2.3: More about e and logs • 175
have a special number e, which we’ll look at in more detail very soon. Back
to our limit, though; we now have
L = lim
h→0
+
((1 + h)
1/h
)
r
= e
r
.
That’s the answer we’re looking for! Let’s put all the above steps together to
see how it flows. With h = r/n, we have
L = lim
n→∞
1 +
r
n
n
= lim
h→0
+
(1 + h)
r/h
= lim
h→0
+
((1 + h)
1/h
)
r
= e
r
.
This means that if you compound more and more frequently at an annual
rate of r, your fortune will increase by an amount very close to e
r
, but never
more than that. The quantity e
r
is the “fortune-increase limit” we’ve been
looking for. The only way you get this rate of increase is if you compound
continuously—that is, all the time!
So, suppose you start with $A in cash and put it in a bank account which
compounds continuously at an annual interest rate of r. After 1 year, you’ll
have $Ae
r
. After two years, you’ll have $Ae
r
× e
r
= Ae
2r
. It’s easy to keep
repeating this and see that after t years, you’ll have $Ae
rt
. It actually works
for partial years as well, because of the exponential rules. So, starting with
$A, we have:
fortune after t years, compounded continuously
at a rate of r per year = Ae
rt
.
Compare this to the formula for compounding n times a year on the previous
page. The quantities A(1 + r/n)
nt
and Ae
rt
look quite different, but for large
n they’re almost the same.
9.2.3 More about e and logs
Let’s take a closer look at our number e. Remembering that
lim
n→∞
1 +
r
n
n
= e
r
,
we can replace r by 1 to get
lim
n→∞
1 +
1
n
n
= e.
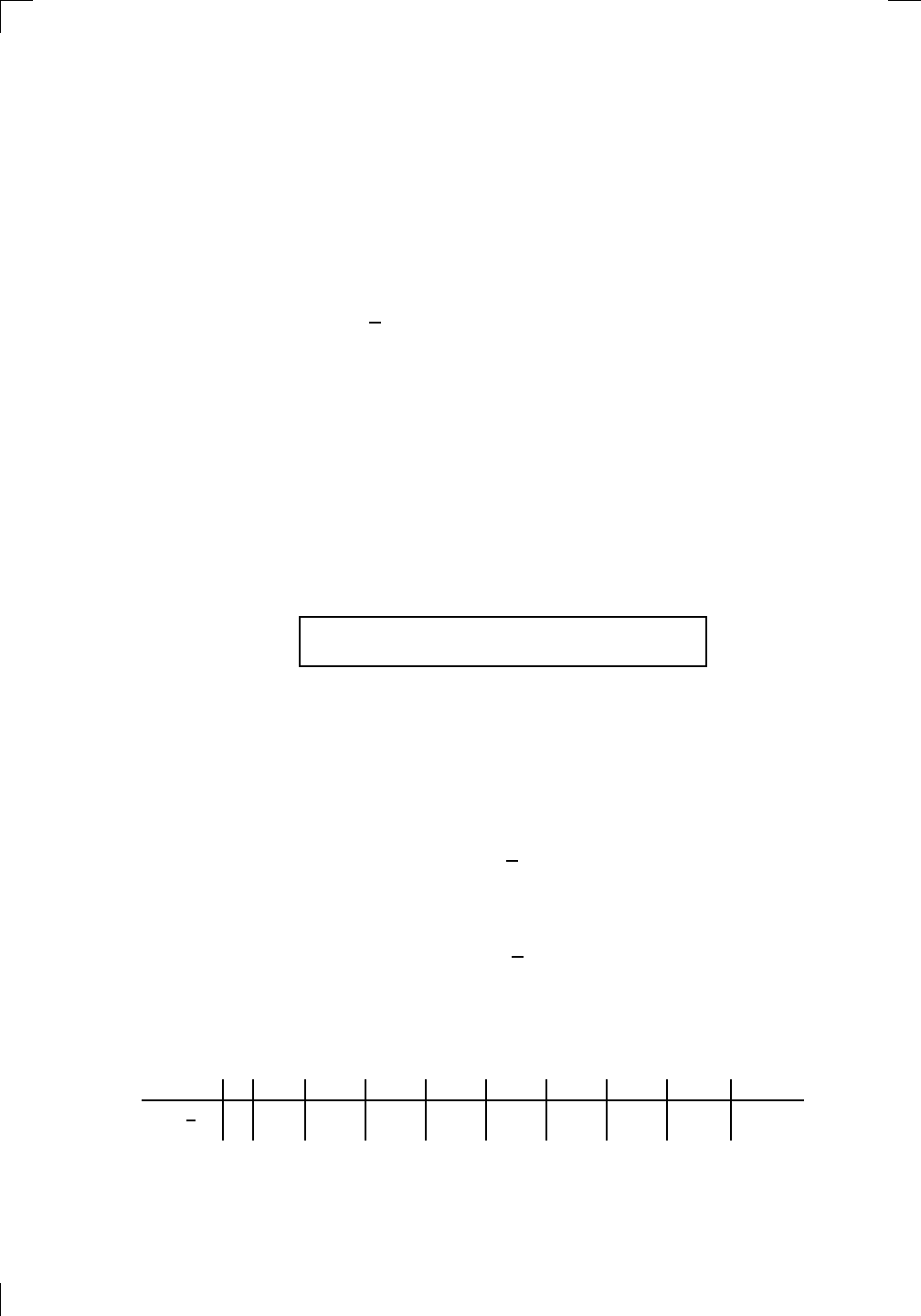
Of course, r = 1 corresponds to an interest rate of 100% per year. Let’s draw
up a little table of values of (1 + 1/n)
n
to three decimal places for some
different values of n:
n 1 2 3 4 5 10 100 1000 10000 100000
`
1 +
1
n
´
n
2 2.25 2.353 2.441 2.488 2.594 2.705 2.717 2.718 2.718
Even compounding once a year at this humongous interest rate doubles your
money (that’s the “2” in the bottom row of the second column). Still, it
