Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


40 CHAPTER 2 Modeling of Vibratory Systems
where the area moment of inertia is given by
(b)
because the bending axis is along the Y direction. Since each of the four flex-
ures experiences the same displacement at its end in the Z direction, this is a
combination of four stiffness elements in parallel; hence, the equivalent stiff-
ness of the system is given by
(c)
Thus,
N/m
N/m (d)
EXAMPLE 2.7
Equivalent stiffness of springs in parallel: removal of a restriction
Let us reexamine the pair of springs in parallel shown in Figure 2.6b. Now,
however, we remove the restriction that the bar to which the force is applied
has to remain parallel to its original position. Then, we have the configuration
shown in Figure 2.12. The equivalent spring constant for this configuration
will be determined.
9.6
k
e
481150 10
9
212 10
6
212 10
6
2
3
121100 10
6
2
3
48 EI
L
3
k
e
4 k
flexure
I
bh
3
12
X
Y
L
b
Mass
Flexure
FIGURE 2.11
Fixed-fixed flexure used in a microelectromechanical system. Source: G.K.Fedder, "Simulation
of Microelectromechanical Systems", Ph.D. Dissertation, Department of Electrical Engineering
and Computer Sciences, University of California, Berkeley, CA, (1994). Reprinted with permis-
sion of the author.
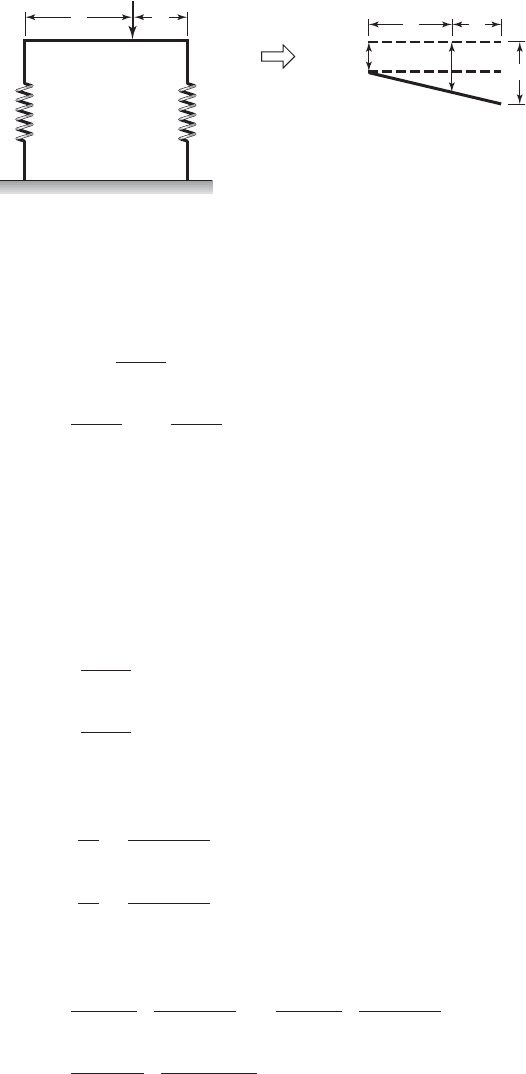
From similar triangles, we see that
(a)
If F
1
is the force acting on k
1
and F
2
is the force acting on k
2
, then from the
summation of forces and moments on the bar we obtain, respectively,
(b)
Thus, Eqs. (b) lead to
(c)
Therefore,
(d)
From Eqs. (a) and (d), we obtain
(e)
F
1a b2
2
c
k
2
b
2
k
1
a
2
k
1
k
2
d
x
b
1a b2
c
bF
k
1
1a b2
d
a
1a b2
c
aF
k
2
1a b2
d
x
2
F
2
k
2
aF
k
2
1a b2
x
1
F
1
k
1
bF
k
1
1a b2
F
2
aF
a b
F
1
bF
a b
bF
2
aF
1
F F
1
F
2
b
a b
x
1
a
a b
x
2
x x
2
b
a b
1x
1
x
2
2
2.3 Stiffness Elements 41
F
k
2
k
1
x
1
x
2
x
ba
b
a
FIGURE 2.12
Parallel springs subjected to unequal forces.

Comparing Eq. (e) to the form
(f)
we find that the equivalent spring constant k
e
is given by
(g)
It is noted that Eq. (g) resembles Eq. (2.16), which was obtained for two
springs in series. This similarity is due to the fact that Eq. (a) resembles
Eq. (2.15), which takes into account that the spring deflections are unequal.
2.3.3 Nonlinear Springs
Nonlinear stiffness elements appear in many applications, including leaf
springs in vehicle suspensions and uniaxial microelectromechanical devices
in the presence of electrostatic actuation.
6
For a nonlinear spring, the spring
force F(x) is a nonlinear function of the displacement variable x. A series ex-
pansion of this function can be interpreted as a combination of linear and non-
linear spring components.
For a stiffness element with a linear spring element and a cubic nonlin-
ear spring element, the force-displacement relationship is written as
F(x) (2.23)
where a is used to express the stiffness coefficient of the nonlinear term in
terms of the linear spring constant k. (This notation will be used later in Sec-
tions 4.5.1 and 5.10.) The quantity a can be either positive or negative.A spring
element for which a is positive is called a hardening spring, and a spring ele-
ment for which a is negative is called a softening spring. From Eq. (2.23), the
potential energy V is
(2.24)
For a linear stiffness element, the force versus displacement graph is a
straight line, and the slope of this line gives the stiffness constant k. For a
nonlinear stiffness element described by Eq. (2.23), the graph is no longer a
straight line. The slope of this graph at a location x x
l
is given by
associated with
nonlinear spring
element
associated with
linear spring
element
V1x 2
x
0
F1x 2dx
1
2
kx
2
1
4
akx
4
akx
3
Nonlinear spring
element
kx
Linear spring
element
k
e
k
1
k
2
1a b2
2
k
2
b
2
k
1
a
2
x
F
k
e
42 CHAPTER 2 Modeling of Vibratory Systems
⎫
⎬
⎭
⎫
⎬
⎭
⎫
⎬
⎭
⎫
⎬
⎭
6
S. G. Adams et al., “Independent Tuning of Linear and Nonlinear Stiffness Coefficients,” J. Mi-
croelectromechanical Systems, Vol. 7, No. 2 (June 1998).

(2.25)
Thus, in the vicinity of displacements in a neighborhood of x x
l
, the cubic
nonlinear stiffness element may be replaced by a linear stiffness element with
a stiffness constant given by Eq. (2.25).
The constant of proportionality ak for the nonlinear cubic spring is de-
termined experimentally in the same manner that the constant k was deter-
mined for a linear spring, as discussed in Section 2.3.2. The results of a typical
experiment are shown in Figure 2.13. The fitted line is determined using stan-
dard nonlinear curve fitting techniques.
7
EXAMPLE 2.8 Nonlinear stiffness due to geometry
In this example, we discuss two systems to show how linear springs can give
rise to nonlinear effects. One such system is shown in Figure 2.14, where the
stretching of the linear spring is described by using Eq. (2.9). We assume that
when g 0, the spring is under an initial deflection d
o
, and the spring, therefore,
1k 3akx
l
2
2
dF
dx
`
x x
l
1k 3akx
2
20
x x
l
2.3 Stiffness Elements 43
7
The MATLAB function lsqcurvefit from the Optimization Toolbox was used.
50
40
30
20
10
0
10
20
30
40
50
0.1 0.05
0 0.05 0.1
k 118.7 N/m
k 36949.3 N/m
3
F (N)
x (m)
Fitted curve
Data
FIGURE 2.13
Experimentally obtained data used to determine the nonlinear spring constant ak.
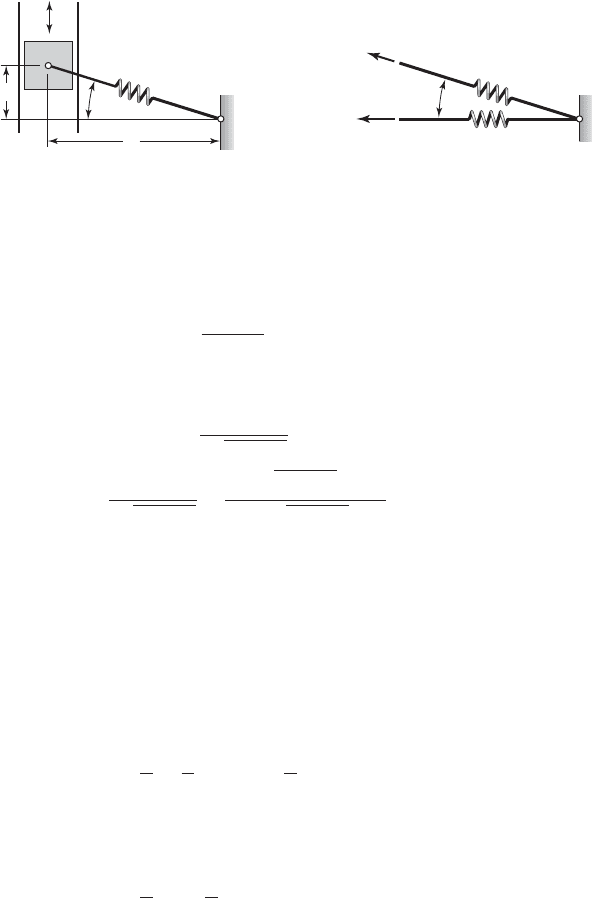
is initially under a tension force T
o
kd
o
. When the spring is moved up or down
an amount x in the vertical direction, the force in the spring is
(a)
The force in the x-direction is obtained from Eq. (a) as
(b)
which clearly shows that the spring force opposing the motion is a nonlinear
function of the displacement x. Hence, a vibratory model of the system shown
in Figure 2.14 will have nonlinear stiffness.
Cubic Springs and Linear Springs
If, in Eq. (b), we assume that |x/L| 1 and expand the denominator of each
term on the right-hand side of Eq. (b) as a binomial expansion and keep only
the first two terms, we obtain
(c)
When the nonlinear term is negligible, Eq. (c) leads to the following linear
relationship
(d)
From Eq. (d), it is seen that the spring constant is proportional to the initial
tension in the spring.
Another example of a nonlinear spring is one that is piecewise linear as
shown in Figure 2.15. Here, each spring is linear; however, as the deflection
increases, another linear spring comes into play and the spring constant
changes (increases). An illustration of the effects of this type of spring on a
vibrating system is given in Section 4.5.1.
F
x
1x 2 kd
o
x
L
T
o
x
L
F
x
1x 2 kd
o
x
L
k
2
1L d
o
2a
x
L
b
3
xkd
o
2L
2
x
2
kx12L
2
x
2
L2
2L
2
x
2
F
x
1x 2 F
s
sin g
F
s
x
2L
2
x
2
F
s
1x 2 kd
o
k12L
2
x
2
L2
44 CHAPTER 2 Modeling of Vibratory Systems
F
s
x
x
L
k
T
o
FIGURE 2.14
Nonlinear stiffness due to geometry: spring under an initial tension, one end of which is
constrained to move in the vertical direction.

2.3.4 Other Forms of Potential Energy Elements
In the previous two subsections, we saw stiffness elements in which the
source of the restoring force is a structural element. Here, we consider other
stiffness elements in which there is a mechanism for storing and releasing po-
tential energy. The source of the restoring force is a fluid element or a gravi-
tational loading.
Fluid Element
As an example of a fluid element, consider the manometer shown in Fig-
ure 2.16 in which the fluid is displaced by an amount x in one leg of the
manometer.
8
Consequently, the fluid has been displaced a total of 2x. If the
fluid has a mass density r and the manometer has an area A
o
, then the magni-
tude of the total force of the displaced fluid acting on the rest of the fluid is
(2.26)
Consequently, the equivalent spring constant of this fluid system is
(2.27)
from which it is clear that the fluid-element stiffness depends on the mass
density r, manometer cross-section area A
o
, and the acceleration due to grav-
ity g. The corresponding potential energy is
(2.28)V1x 2
1
2
k
e
x
2
rgA
o
x
2
2rgA
o
k
e
dF
m
dx
F
m
1x 2 2rgA
o
x
2.3 Stiffness Elements 45
x
x
o
x
o
x
o
x
o
F
FIGURE 2.15
Nonlinear spring composed of a set of linear springs.
g
x
x
A
o
FIGURE 2.16
Manometer.
8
For a proposed practical application of this type of system see: S. D. Xue, “Optimum Parame-
ters of Tuned Liquid Column Damper for Suppressing Pitching Vibration of an Undamped Struc-
ture,” J. Sound Vibration, Vol. 235, No. 2, pp. 639–653 (2000).

Alternatively, the potential energy can also be obtained directly from the
work done
(2.29)
Compressed Gas
Consider the piston shown in Figure 2.17 in which gas is stored at a pressure P
o
and entrained in the volume V
o
A
o
L
o
, where A
o
is the area of the piston and
L
o
is the original length of the cylindrical cavity. Thus, when the piston moves
by an amount x along the axis of the piston, V
o
decreases to a volume V
c
, where
(2.30)
The equation of state for the gas is
(2.31)
When a gas is compressed slowly, the compression is isothermal and n 1.
When it is compressed rapidly, the compression is adiabatic and n c
p
/c
v
, the
ratio of specific heats of the gas, which for air is 1.4. To determine the spring
constant, we note that the magnitude of the force on the piston is
(2.32)
Thus, upon substitution of V
c
given by Eq. (2.30), we obtain
(2.33)
Thus, the pressure-filled gas element provides the stiffness. Equation (2.33)
describes a nonlinear force versus displacement relationship. As discussed
earlier, this relationship may be replaced in the vicinity of x x
l
by a straight
line with a slope k
e
, where k
e
is the stiffness of an equivalent linear stiffness
element. This equivalent stiffness is given by
(2.34a)
For , Eq. (2.34a) is simplified to
(2.34b)k
e
nA
o
P
o
L
o
0x
l
/L
o
0 1
nA
o
P
o
L
o
11 x
l
/L
o
2
n1
k
e
dF
dx
`
x x
l
F1x 2 A
o
c
o
V
o
n
11 x/L
o
2
n
A
o
P
o
11 x/L
o
2
n
F A
o
P A
o
c
o
V
c
n
PV
c
n
P
o
V
o
n
c
o
constant
A
0
L
0
a1
x
L
0
b
V
c
1x 2 V
0
A
0
x
2rgA
o
x
0
xdx rgA
o
x
2
V1x 2
x
0
F
m
1x 2dx
46 CHAPTER 2 Modeling of Vibratory Systems
L
o
V
o
A
o
Gas at P
o
L
o
x
V
x
A
o
Gas at P
FIGURE 2.17
Gas compression with a piston.
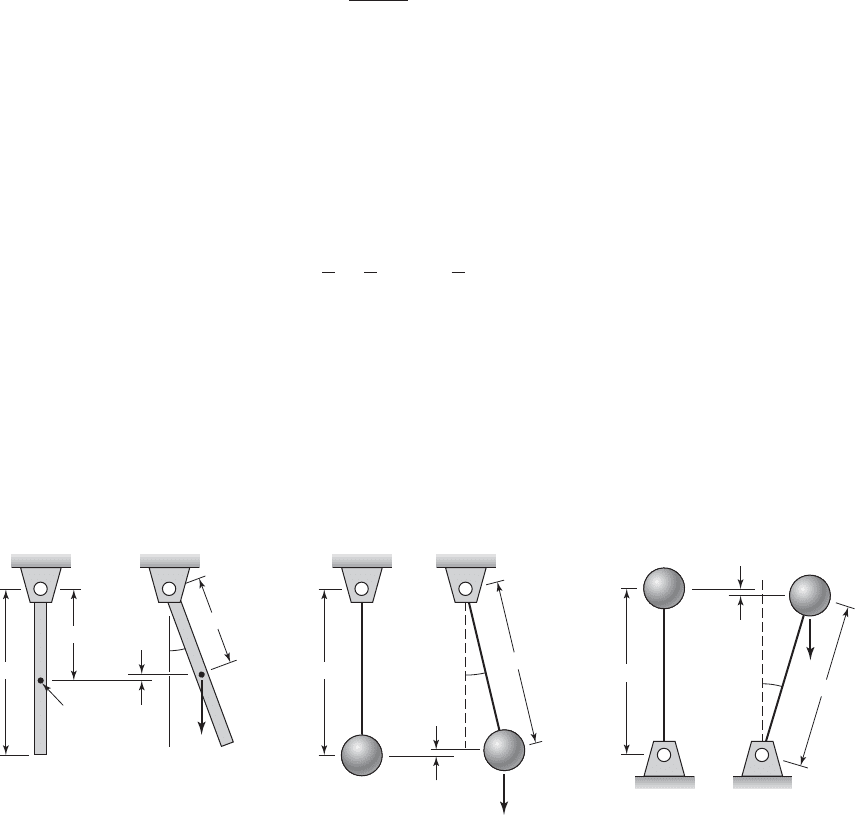
For arbitrary x/L
o
, the potential energy V(x) is determined by using
Eq. (2.33) as
(2.35)
Pendulum System
Figure 2.18(a) Consider the bar of uniformly distributed mass m shown in
Figure 2.18a that is pivoted at its top. Let the reference position be located at
a distance L/2 below the pivot point, where the center of mass is located when
the pendulum is at u 0. When the bar rotates either clockwise or counter-
clockwise, the vertical distance through which the center of gravity of the bar
moves up from the reference position is
(2.36)
Since F mg, the increase in the potential energy is
(2.37a)V1x 2
x
0
F1x 2dx
x
0
mgdx mgx
x
L
2
L
2
cos u
L
2
11 cos u2
A
o
P
o
L
o
n 1
311 x/L
o
2
1n
14
n 1
A
o
P
o
L
o
ln11 x/L
o
2
n 1
V1x 2
x
0
F1x 2dx A
o
P
o
x
0
11 x/L
o
2
n
dx
2.3 Stiffness Elements 47
m
1
g
m
1
g
L L
L
L
L
x
x
L/2
(b)(a) (c)
L/2
c.g.
mg
x
m
1
m
1
FIGURE 2.18
Pendulum systems: (a) bar with uniformly distributed mass; (b) mass on a weightless rod; and (c) inverted mass on a weightless rod.

or, from Eq. (2.36),
(2.37b)
When the angle of rotation u about the upright position u 0 is “small,”
we can use the Taylor series approximation
9
(2.38)
and substitute this expression into Eq. (2.37b) to obtain
(2.39)
where the equivalent spring constant is
(2.40)
Figure 2.18(b) In a similar manner, for “small” rotations about the upright
position u 0 in Figure 2.18b, we obtain the increase in potential energy for
the system. Here it is assumed that a weightless bar supports the mass m
1
.
Choosing the reference position as the bottom position, we obtain
(2.41)
where the equivalent spring constant is
(2.42)
In the configuration shown in Figure 2.18b, if the weightless bar is re-
placed by one that has a uniformly distributed mass m, then the total potential
energy of the bar and the mass is
(2.43)
where the equivalent spring constant is
(2.44)
Figure 2.18(c) When the pendulum is inverted as shown in Figure 2.18c,
then there is a decrease in potential energy; that is,
(2.45)V1u 2
1
2
m
1
gLu
2
k
e
a
m
2
m
1
bgL
V1u 2
1
4
mgLu
2
1
2
m
1
gLu
2
1
2
a
m
2
m
1
bgLu
2
1
2
k
e
u
2
k
e
m
1
gL
V1u 2
1
2
m
1
gLu
2
1
2
k
e
u
2
k
e
mgL
2
V1u 2
1
2
a
mgL
2
bu
2
1
2
k
e
u
2
cos u 1
u
2
2
p
V1u 2
mgL
2
11 cos u2
48 CHAPTER 2 Modeling of Vibratory Systems
9
T. B. Hildebrand, Advanced Calculus for Applications, Prentice Hall, Englewood Cliffs NJ
(1976).
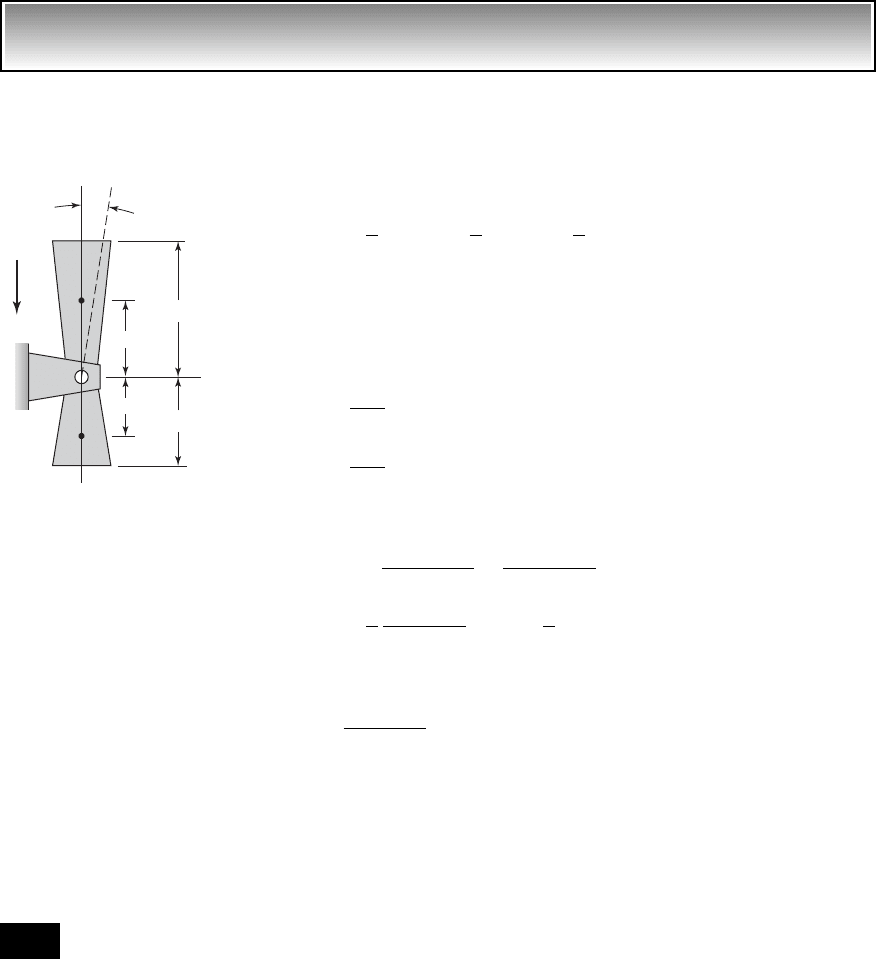
EXAMPLE 2.9 Equivalent stiffness due to gravity loading
Consider the pivoted bar shown in Figure 2.19. The lower portion of the bar
has a mass m
1
and the upper portion a mass m
2
. The distance of the center of
gravity of the upper portion of the bar to the pivot is a and the distance of the
center of gravity of the lower portion of the bar to the pivot is b. For “small”
rotations about the upright position u 0, the potential energy is
(a)
There is a gain or loss in potential energy depending on whether m
1
b m
2
a
or vice versa.
A special case of Eq. (a) is when the bar has a uniformly distributed mass
m so that
(b)
where L L
1
L
2
. Then, since b L
1
/2 and a L
2
/2, Eq. (a) becomes
(c)
where the equivalent stiffness k
e
is
(d)
Hence, the stiffness is due to gravity loading. When L
1
L
2
, V 0. It is men-
tioned that if the systems were to lie in the plane of the page, that is, normal
to the direction of gravity, then there is no restoring force when the bar is ro-
tated an amount u and these relationships are not applicable. Furthermore,
when L
2
0, Eq. (d) reduces to Eq. (2.40) with L replaced by L
1
.
2.4 DISSIPATION ELEMENTS
Damping elements are assumed to have neither inertia nor the means to store
or release potential energy. The mechanical motion imparted to these ele-
ments is converted to heat or sound and, hence, they are called nonconserva-
tive or dissipative because this energy is not recoverable by the mechanical
system. There are four common types of damping mechanisms used to model
vibratory systems. They are (i) viscous damping, (ii) Coulomb or dry friction
k
e
1L
1
L
2
2
2
mg
1
2
1L
1
L
2
2
2
mg u
2
1
2
k
e
u
2
V1u 2 a
L
1
2
41L
1
L
2
2
L
2
2
41L
1
L
2
2
bmg u
2
m
2
mL
2
L
m
1
mL
1
L
V1u 2
1
2
m
1
gbu
2
1
2
m
2
gau
2
1
2
1m
1
b m
2
a2gu
2
2.4 Dissipation Elements 49
L
2
L
1
m
1
m
2
b
a
g
FIGURE 2.19
Pivoted bar with unequally distrib-
uted mass along its length.
