Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

ﬁxed at both ends, while the beam model used for the work piece is consid-

ered ﬁxed at one end and hinged or free at the other end where it is being cut.

In Section 4.4, the stability of a machine tool is determined from a vi-

bratory model to avoid undesirable cutting conditions called chatter. This type

of analysis can be used to choose parameters such as width of cut, spindle

rpm, etc. In Chapter 9, vibrations of beams used in the model in Figure 2.27

are discussed at length.

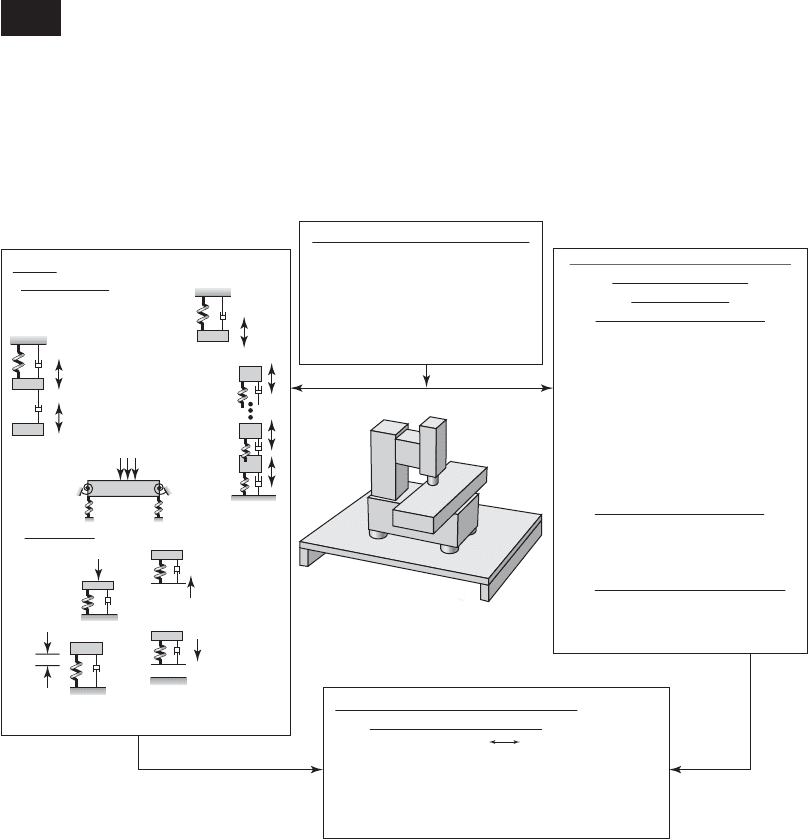
2.6 DESIGN FOR VIBRATION

Principles that govern single degree-of-freedom systems, multiple degree-of-

freedom systems, and continuous vibratory systems are covered in this book

and are presented along with information needed to experimentally, numeri-

cally, and analytically investigate a vibratory system. In Figure 2.28, we show

60 CHAPTER 2 Modeling of Vibratory Systems

Mass

Stiffness

Linear

Nonlinear

Damping

Viscous

Fluid

Material

Dry friction

System Characterization

Natural frequency

Impulse response

Transfer function

Excitation Characterization

Harmonic

Transient

Random

Design for Vibration Objectives

Isolation

Absorption

Natural frequency

Damping ratio

Filter

Mode shape

Numerical Evaluation and Analysis

Response Characteristics

Time Domain Frequency Domain

Displacement

Velocity

Acceleration

Force at base

System

Experiments and Measurements

Data Collection and

Interpretation

Parameter Identification

Model

Assumptions

1 degree-of-freedom

2 degree-of-freedom

degree-of-freedom

Beam

Excitation

Force

Base

Velocity

Displacement

FIGURE 2.28

Design for vibration.

Exercises 61

EXERCISES

Section 2.1

2.1 Examine Eqs. (2.1) and (2.5) and verify that the

units (dimensions) of the different terms in the re-

spective equations are consistent.

Section 2.2

2.2 Consider the slider mechanism of Example 2.2 and

show that the rotary inertia J

O

about the pivot point O

is also a function of the angular displacement w.

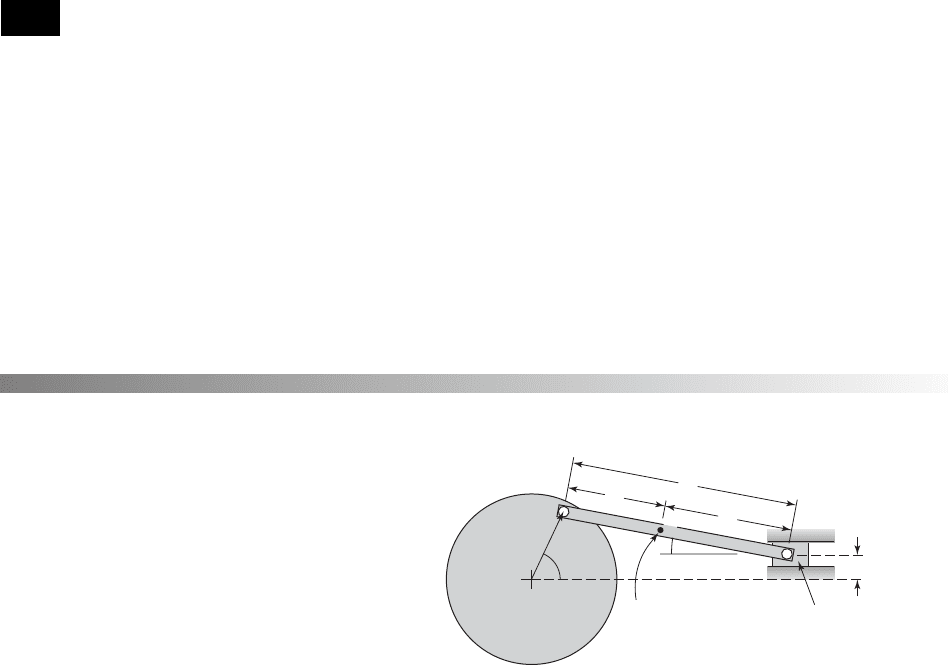
2.3 Consider the crank-mechanism system shown in

Figure E2.3. Determine the rotary inertia of this sys-

tem about the point O and express it as a function of

the angular displacement u. The disc has a rotary

inertia J

about the point O. The crank has a mass m

and rotary inertia J

about the point G at the center of

mass of the crank. The mass of the slider is m

Section 2.3.2

2.4 Find the equivalent length L

of a spring of con-

stant cross section of diameter d

that has the same

spring constant as the tapered spring shown in Case 2

of Table 2.3. Both springs have the same Young’s

modulus E.

2.5 Extend the spring combinations shown in Figures

2.6b and 2.6c to cases with three springs. Verify that

the equivalent stiffness of these spring combinations

is consistent with Eqs. (2.14) and (2.16), respectively.

2.6 Consider the mechanical spring system shown in

Figure E2.6. Assume that the bars are rigid and

determine the equivalent spring constant k

, which we

can use in the relation F  k

how these different aspects are used to design a system to have speciﬁc vi-

bratory characteristics.

2.7 SUMMARY

In this chapter, the inertia elements, stiffness elements, and dissipation ele-

ments that are used to construct a vibratory model were discussed. An ideal in-

ertia element, which does not have any stiffness or dissipation characteristics,

can store or release kinetic energy. An ideal stiffness element, which does not

have any inertia or dissipation characteristics, can store or release potential en-

ergy. The stiffness element can be due to a structure, a ﬂuid element, or gravity

loading. The notion of equivalent stiffness has been introduced. An ideal dissi-

pation element, which does not have any stiffness or inertia characteristics, is

used to represent energy losses of the system. The notion of equivalent damp-

ing has also been introduced.

, J





FIGURE E2.3

62 CHAPTER 2 Modeling of Vibratory Systems

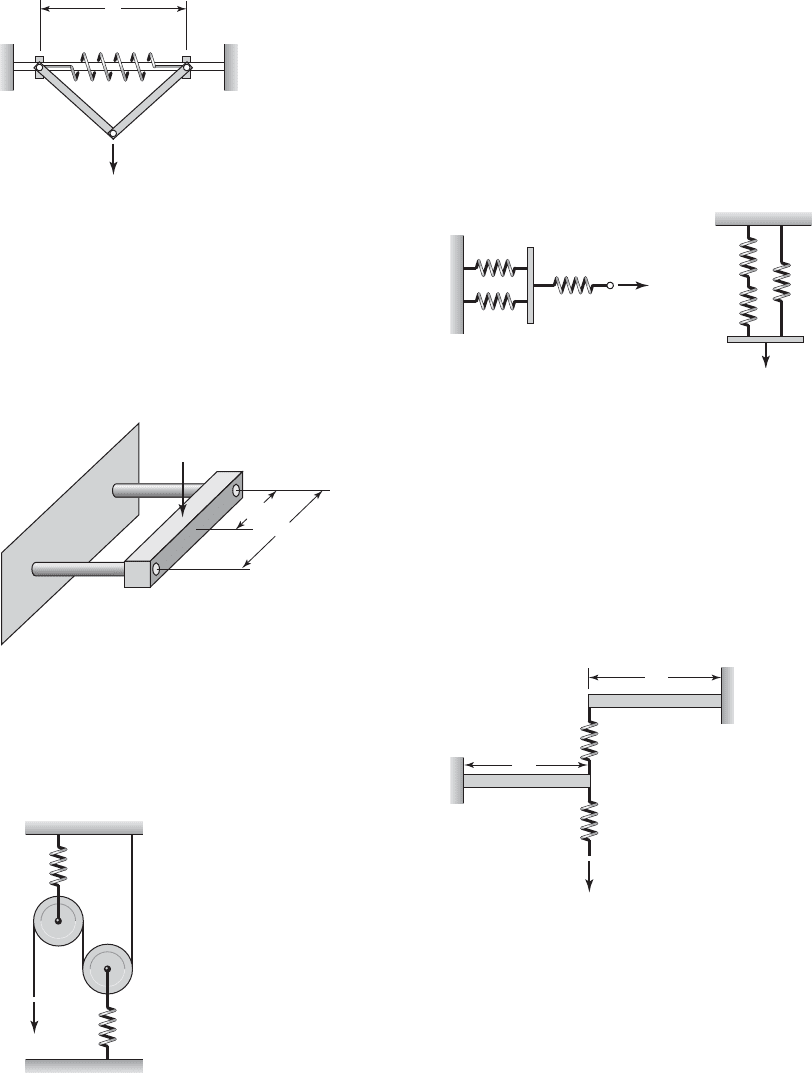
2.7

Consider the three beams connected as shown in

Figure E2.7. The beam that is attached to the ends of

the two cantilever beams is pinned so that its ends can

rotate unimpeded. Determine the system’s equivalent

spring constant for the transverse loading shown.

2.10 For the two cantilever beams whose free ends are

connected to springs shown in Figure E2.10, give the

expressions for the spring constants k

and k

and

determine the equivalent spring constant k

for the

system.

L/2

E, I

, I

, L

, I

, L

FIGURE E2.7

2.8 For the weightless pulley system shown in Fig-

ure E2.8, determine the equivalent spring constant.

F, x

FIGURE E2.8

Recall that when the center of the pulley moves by an

amount x, the rope moves an amount 2x.

2.9 Determine the equivalent stiffness for each of the

systems shown in Figure E2.9. Each system consists

of three linear springs with stiffness k

, k

, and k

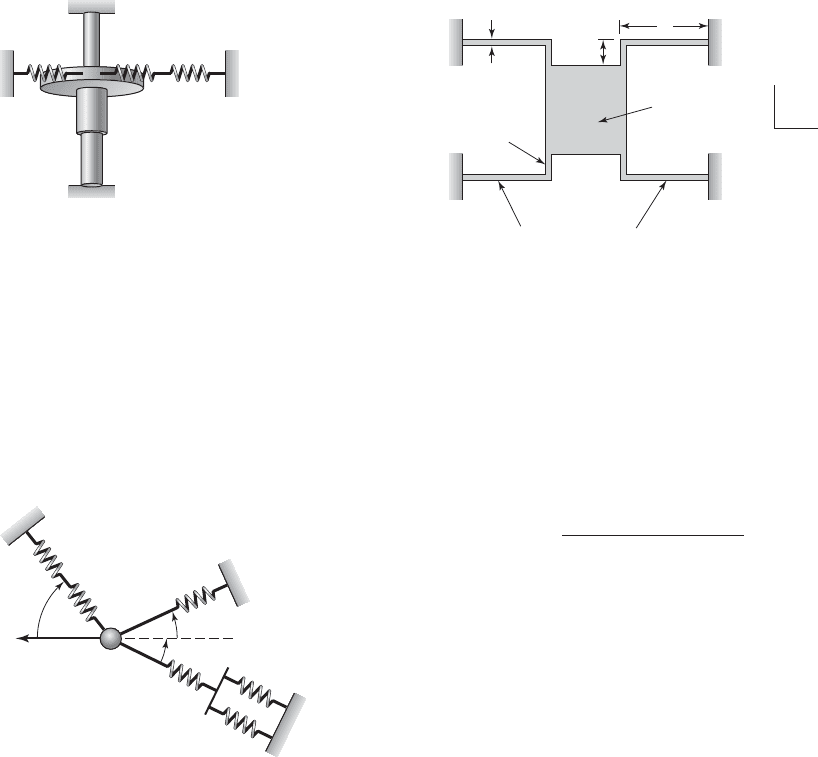
2.11 For the system of translation and torsion springs

shown in Figure E2.11, determine the equivalent

spring constant for torsional oscillations. The disc has

a radius b, and the translation springs are tangential to

the disc at the point of attachment.

FIGURE E2.9

, I

FIGURE E2.10

F, x

FIGURE E2.6

Exercises 63

2.12

For the system of translation springs shown

in Figure E2.12, determine the equivalent spring

constant for motion in the horizontal (x) direction

only. Assume that so that the u

remain

constant.

0¢x 0 1

The equivalent stiffness of each of these ﬂexures

in the X-direction can be shown to be

where the Young’s modulus of elasticity is E, which

has a value of 160 GPa for the polysilicon material

from which the ﬂexure is fabricated. The dimensions

of each crab leg are as follows: L  100 m and

b  b

 h  2 m. For the thigh length L

spanning

the range from 10 m to 75 m, plot the graph of the

equivalent stiffness of the system versus L

2.14 Based on the expression for k

ﬂexure

provided in

Exercise 2.13, the sensitivity of the equivalent stiff-

ness of each ﬂexure with respect to the ﬂexure width

b and the thigh width b

can be assessed by determin-

ing the derivatives dk

ﬂexure

/db and dk

ﬂexure

/db

, respec-

tively. Carry out these operations and discuss the ex-

pressions obtained.

2.15 Find the torsion-spring constant k

of the stepped

shaft shown in Figure E2.15, where each shaft has the

same shear modulus G. Determine the equivalent

spring length of a shaft of constant diameter D

and

length L

that has the same spring constant as the tor-

sion spring shown in Figure E2.15.

ﬂexure



Ehb

14L  L

1b/b

1L  L

1b/b

2.13 Consider the system shown Figure E2.13, which

lies in the X–Y plane. This system, which is called a

crab-leg ﬂexure, is used in microelectromechanical

sensors. A load along the X direction is applied to the

mass to which all of the four crab-leg ﬂexures are at-

tached. Each ﬂexure has a shin of length L along

the X direction, width b along the Y direction, and

thickness h along the Z direction. The thigh of each

ﬂexure has a length L

along the Y direction, a width b

along the X direction, and a thickness h along the

Z direction.

FIGURE E2.11

FIGURE E2.12

Mass

Thigh

ShinCrab-leg ﬂexture

FIGURE E2.13

Source: G.K.Fedder, "Simulation of Microelectromechanical Sys-

tems", Ph.D. Dissertation, Department of Electrical Engineering

and Computer Sciences, University of California, Berkeley, CA,

(1994). Reprinted with permission of the author.



  

  

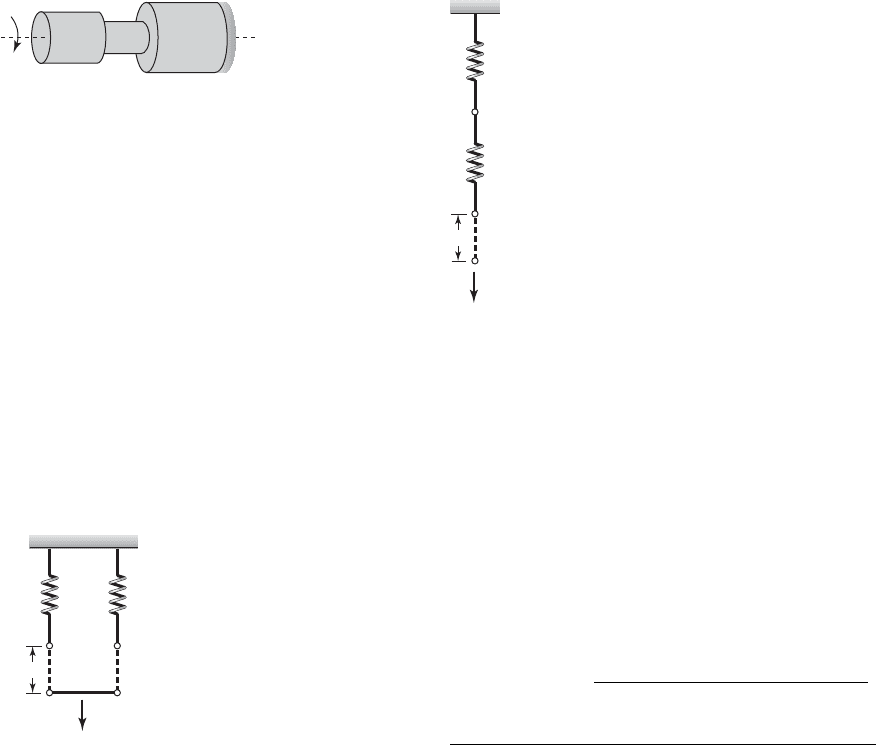
64 CHAPTER 2 Modeling of Vibratory Systems

2.18

Consider the data in Table E2.18 in which the

experimentally determined tire loads versus tire de-

ﬂections have been recorded. These data are for a set

of dual tires and a single wide-base tire.

The inﬂa-

tion pressure for all tires is 724 kN/m

. Examine the

stiffness characteristics of the two different tire sys-

tems and discuss them.

2.17 Consider the two nonlinear springs in series

shown in Figure E2.17. The force-displacement rela-

tions for each spring are, respectively,

a) Obtain the expressions from which the equivalent

spring constant can be determined.

b) If F  1000 N, k

 50,000 N/m, k

 25,000 N/m,

and a  2m

2

, determine the equivalent spring

constant.

1x 2 k

x  k

j  1, 2

(x)F

(x)

FIGURE E2.16

J. C. Tielking, “Conventional and wide base radial tyres,” in Pro-

ceedings of the Third International Symposium on Heavy Vehicle

Weights and Dimensions, D. Cebon and C. G. B. Mitchell, eds.,

Cambridge, UK, 28 June–2 July 1992, pp. 182–190.

TABLE E2.18

Tire Load Versus Deﬂection Data

Tire Deﬂection

Tire Load Dual Tire Single Wide-Base

(N) (mm) Tire (mm)

00 0

8896.4 7.62 10.2

17793 14 19

26689 19 27.9

35586 24.1 35.6

44482 27.9 41.9

Section 2.3.4

2.19 Consider the manometer shown in Figure 2.16

and seal the ends. Assume that the initial gas pressure

of the sealed system is P

and that L

is the initial

Section 2.3.3

2.16 Consider the two nonlinear springs in parallel that

are shown in Figure E2.16. The force-displacement

relations for each spring are, respectively,

a) Obtain the expressions from which the equivalent

spring constant can be determined.

b) If F  1000 N, k

 k

 50,000 N/m, and a 

2

, determine the equivalent spring constant.

1x 2 k

x  k

j  1, 2

, D

FIGURE E2.15

(x)

FIGURE E2.17

Exercises 65

2.22

Determine the equivalent damping for the system

shown in Figure E2.22.

length of the cavity. Determine the equivalent spring

constant of the system when the column of liquid un-

dergoes “small” displacements.

2.20 Consider “small” amplitude angular oscillations

of the pendulum shown in Figure E2.20. Considering

the gravitational loading and the torsion spring k

the pivot point, determine the expression for the sys-

tem’s equivalent spring constant. The masses are held

with rigid, weightless rods for the loading shown.

FIGURE E2.20

Section 2.4.1

2.21 Determine the equivalent damping of the system

shown in Figure E2.21.

FIGURE E2.21

FIGURE E2.22

TABLE E2.23

Racecar Damper

Damper Force Damper Rod Speed

Magnitude (N) (mm/s)

57.83 2.54

115.7 5.08

177.9 7.62

266.9 10.2

355.9 12.7

444.8 15.2

489.3 17.8

533.8 20.3

578.3 22.9

622.8 25.4

667.2 27.9

711.7 30.5

756.2 33

800.7 35.6

845.2 38.1

889.6 40.6

Racecar dampers are called “shocks” in the United States, and

they have different damping characteristics during compression

(called “bump”) and expansion (called “rebound”) phases. For ma-

terial on racecar damping, see, for example, P. Haney and J. Braun,

Inside Racing Technology, (ISBN 0-9646414-0-2).

2.24 Determine the viscosity of the ﬂuid that one

needs to use to realize a parallel-plate damper when

the top plate has an area of 0.02 m

, the gap between

the parallel plates h  0.2 mm, and the required

damping coefﬁcient is 20 N s/m.

2.23 Representative damping-force magnitudes ver-

sus speed data are given in Table E2.23 for a racecar

damper in compression.

Examine these data and dis-

cuss the type of damping model that can be used to

represent them.

66 CHAPTER 2 Modeling of Vibratory Systems

response, is possible when a vibratory system is ex-

cited by a harmonic force. Evaluate the work done by

the spring force and the work done by the damper

force, which are given by the integrals

2.29 For the system of Exercise 2.28, assume

k  1000 N/m, c  2500 N/(m/s), X

 0.1 m, and

v  9 rad/s. Plot the graph of the sum of the spring

force and damper force versus the displacement; that

is, versus x.

2.30 For the system of Exercise 2.28, assume that

k  0, c  0, and v  0. Show that the graph of

versus x will have the form of an ellipse.

Section 2.4.2

2.31 Consider the viscous-damping model given by

Eq. (2.46) and the dry-friction model given by

Eq. (2.52). Sketch the force versus velocity graphs

in each case for the following parameter values: c 

100 N/(m/s), m  100 kg, and m  0.1.

2.32 Normalize the linear viscous-damper force given

by Eq. (2.46) using the damping coefﬁcient c, the dry

friction force given by Eq. (2.52) using mmg, the

ﬂuid-damping force given by Eq. (2.54) using the

damping coefﬁcient c

, and the hysteretic force

given by Eq. (2.57) using kpb

. Plot the time histories

of the normalized damper forces versus time

for harmonic displacement of the form x(t) 

0.4sin (2pt) m. Discuss the characteristics of these

plots.

2.33 Construct vibratory models for each of the three

systems shown in the Figure E2.33. Discuss the num-

kx  cx





x12p/v2

x102

dx 



2p/v





x12p/v2

x102

kxdx 



2p/v

kxx

2.27 Represent the vibratory system given in Fig-

ure E2.27 as an equivalent vibratory system with mass

m, equivalent stiffness k

, and equivalent damping

coefﬁcient c

FIGURE E2.27

2.25 Determine the equivalent damping coefﬁcient for

the following nonlinear damper:

where c

= 5 N s/m and c

= 0.6 N s

. Note: the

damper is to be operated around a speed of 5 m/s.

2.26 Represent the vibratory system given in Fig-

ure E2.26 as an equivalent vibratory system with

mass m, equivalent stiffness k

, and equivalent damp-

ing coefﬁcient c

F1x

2 c

 c

FIGURE E2.26

2.28 The vibrations of a system with stiffness k and

damping coefﬁcient c is of the form x(t)  X

sin vt.

This type of response, which is called a harmonic

ber of degrees of freedom and the associated general-

ized coordinates in each case.

2.34 A vibratory system has a mass m  10 kg,

k  1500 N/m, and c  2500 N/(m/s). Given that

the displacement response has the form x(t) 

0.2sin(9t) m, plot the graphs of , the spring force

kx, and the damper force versus time and discuss

them.

Exercises 67

(a)

(b)

(c)

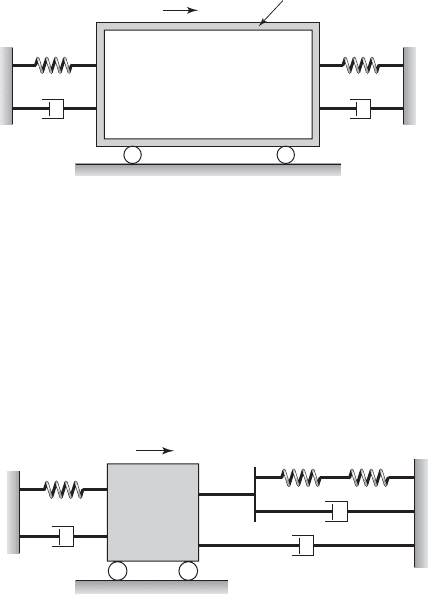
FIGURE E2.33

Springs, masses, and dampers are used to model vibrations systems. In the motorcycle, the coil spring in parallel with a viscous

damper is attached to a mass composed of the tire and brake assembly. In the wind turbine, the mass of the propellers is supported

by the column, which acts as the spring. (Source: Cohen/Ostrow / Getty Images; PKS Media, Inc. / Getty Images.)

6969

Single Degree-of-Freedom Systems:

Governing Equations

3.1 INTRODUCTION

3.2 FORCE-BALANCE AND MOMENT-BALANCE METHODS

3.2.1 Force-Balance Methods

3.2.2 Moment-Balance Methods

3.3 NATURAL FREQUENCY AND DAMPING FACTOR

3.3.1 Natural Frequency

3.3.2 Damping Factor

3.4 GOVERNING EQUATIONS FOR DIFFERENT TYPES

OF DAMPING

3.5 GOVERNING EQUATIONS FOR DIFFERENT TYPES OF

APPLIED FORCES

3.5.1 System with Base Excitation

3.5.2 System with Unbalanced Rotating Mass

3.5.3 System with Added Mass Due to a Fluid

3.6 LAGRANGE’S EQUATIONS

3.7 SUMMARY

EXERCISES

3.1 INTRODUCTION

In this chapter, two approaches are illustrated for deriving the equation gov-

erning the motion of a single degree-of-freedom system. The momentum

principles of Chapter 1 form the basis of one approach, comprising force-

balance and moment-balance methods. The second approach is based on La-

grange’s equations, ﬁrst introduced in this chapter and extensively used

throughout the remaining chapters. Based on the parameters that appear in the