Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

70 CHAPTER 3 Single Degree-of-Freedom Systems

governing equation, the expressions for the natural frequency and damping

factor are deﬁned. The full physical signiﬁcance of the natural frequency and

damping factor is brought forth in Section 4.2, when free oscillations of sin-

gle degree-of-freedom systems are considered. Furthermore, system stability

can also be assessed from the system parameters, as discussed in Section 4.3.

When either an analytical or a numerical solution of the governing equa-

tion is obtained, one can determine the relative effects that the system’s com-

ponents have on the system’s response to various externally applied forces

and initial conditions. One can also study vibratory systems by determining

the transfer function of the system (Section 5.3) or the system’s impulse

response (Section 6.2). In this chapter, we will only derive the governing

equations for various systems. We shall then obtain the general solutions in

Chapter 4 and Appendix D and illustrate numerous applications and interpre-

tations of the solutions in Chapters 4, 5, and 6.

In this chapter, we shall show how to:

• Obtain the governing equation of motion for single degree-of-freedom

translating and rotating systems by using force balance and moment bal-

ance methods.

• Obtain the governing equation of motion for single degree-of-freedom

translating and rotating systems by using Lagrange’s equations.

• Determine the equivalent mass, equivalent stiffness, and equivalent damp-

ing of a single degree-of-freedom system.

• Determine the natural frequency and damping factor of a system.

3.2 FORCE-BALANCE AND MOMENT-BALANCE METHODS

In this section, we illustrate the use of force-balance and moment-balance

methods for deriving governing equations of motion of single degree-of-

freedom systems, show how the static-equilibrium position of a vibratory sys-

tem can be determined, and carry out linearization of a nonlinear system for

“small” amplitude oscillations about a system’s equilibrium position.

3.2.1 Force-Balance Methods

Consider the principle of linear momentum, which is Newton’s second law of

motion. The statement of dynamic equilibrium given by Eq. (1.11) is recast in

the form

(3.1a)

where F is the net external force vector acting on the system, p is the absolute

linear momentum of the considered system and the overdot indicates the de-

rivative with respect to time. For a system of constant mass m whose center

of mass is moving with absolute acceleration a, the rate of change of linear

momentum and Eq. (3.1a) lead to

(3.1b)F  ma  0

 ma

F  p

 0

3.2 Force Balance and Moment-Balance Methods 71

The term ma is referred to as the inertia force. The interpretation of

Eq. (3.1b) is that the sum of the external forces and inertial forces acting on

the system is zero; that is, the system is in equilibrium under the action of

external and inertial forces.

Vertical Vibrations of a Spring-Mass-Damper System

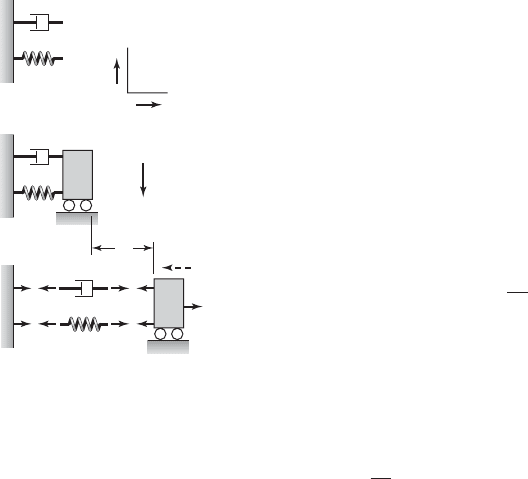
In Figure 3.1, a spring-mass-damper model is shown. A linear spring with

stiffness k and a viscous damper with damping coefﬁcient c are connected in

parallel to the inertia element m. In addition to the three system elements that

were discussed in Chapter 2, an external forcing is also considered. We would

like to obtain an equation to describe the motions of the system in the verti-

cal direction. In order to derive such an equation for translation motions, the

force-balance method is used. Prior to obtaining the governing equation of

motion for the system of Figure 3.1, we choose a set of orthogonal unit vec-

tors i and j ﬁxed in an inertial reference frame and a coordinate system with

X and Y axes and an origin O that is ﬁxed. Since the mass m translates only

along the j direction, the force balance is considered only along this direction.

Let the unstretched length of the spring shown in Figure 3.1 be L. Then

the mass is located at the position from the ﬁxed surface,

where the term d

will be determined shortly and explained. After determin-

ing d

, the equation of motion will be developed in terms of the displacement

variable x. The position vector of the mass from the ﬁxed point O is given by

(3.2)r  rj  1L  d

 x2j

1L  d

 x2j

Equilibrium

position (x  0)

k(x  

)



k(x  

) cx

f(t)

This statement is also referred to as D’Alembert’s principle. According to the generalized form

of this principle, when a set of so-called virtual displacements are imposed on the system of in-

terest, the net work done by the external forces and inertial forces is zero. [See, for example,

D. T. Greenwood, Principles of Dynamics, Chapter 8, Prentice Hall, Upper Saddle River, NJ

(1988).]

FIGURE 3.1

Vertical vibrations of a spring-mass-damper system.

The directions of different forces along with their magnitudes are shown in

Figure 3.1. Note that the inertia force is also shown along with the free-

body diagram of the inertia element. Since the spring force is a restoring force

and the damper force is a resistive force, they oppose the motion as shown in

Figure 3.1. Based on Eq. (3.1b), we can carry out a force balance along the

j direction and obtain the resulting equation

(3.3)

External forces acting Spring force acting Damping force Inertia force

on system on mass acting on mass

Upon making use of Eq. (3.2), noting that L and d

are constants, and rear-

ranging terms, Eq. (3.3) reduces to the following scalar differential equation

(3.4)

Static-Equilibrium Position

The static-equilibrium position of a system is the position that corresponds to

the system’s rest state; that is, a position with zero velocity and zero acceler-

ation. Dropping the time-dependent forcing term f(t) and setting the velocity

and acceleration terms in Eq. (3.4) to zero, we ﬁnd that the static-equilibrium

position is the solution of

(3.5)

If, in Eq. (3.5), we choose

(3.6)

we ﬁnd that x  0 is the static-equilibrium position of the system. Equa-

tion (3.6) is interpreted as follows. Due to the weight of the mass m, the spring

is stretched an amount , so that the spring force balances the weight mg. For

this reason, is called the static displacement. Recalling that the spring has

an unstretched length L, the static-equilibrium position measured from the

origin O is given by

(3.7)

which is the rest position of the system. For the vibratory system of Fig-

ure 3.1, it is clear from Eq. (3.6) that the static-equilibrium position is deter-

mined by the spring force and gravity loading. An example of another type of

static loading is provided in Example 3.1.

Equation of Motion for Oscillations about the Static-Equilibrium Position

Upon substituting Eq. (3.6) into Eq. (3.4), we obtain

(3.8)m

 c

 kx  f 1t 2

 x

j  1L  d



k1x  d

2 mg

 c

 k1x  d

2 f 1t 2 mg

f 1t 2j  mg j  1kx  kd

2j  c

j  m

j  0

mx

72 CHAPTER 3 Single Degree-of-Freedom Systems

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

Equation (3.8) is the governing equation of motion of a single degree-of-

freedom system for oscillations about the static-equilibrium position given by

Eq. (3.7). Note that the gravity loading does not appear explicitly in Eq. (3.8).

For this reason, in development of models of linear vibratory systems, the

measurement of displacement from the static-equilibrium position turns out

to be a convenient choice, since one does not have to explicitly take the static

loading into account.

The left-hand side of Eq. (3.8) describes the forces from the components

that comprise a single degree-of-freedom system. The right-hand side repre-

sents the external force acting on the mass. Examples of external forces act-

ing on a mass are ﬂuctuating air pressure loading such as that on the wing of

an aircraft, ﬂuctuating electromagnetic forces such as in a loudspeaker coil,

electrostatic forces that appear in some microelectromechanical devices,

forces caused by an unbalanced mass in rotating machinery (see Section 3.5),

and buoyancy forces on ﬂoating systems. The system represented by Eq. (3.8)

is a linear, ordinary differential equation with constant coefﬁcients m, c,

and k. As mentioned in Sections 2.2, 2.3, and 2.4, these quantities are also

referred to as system parameters.

Horizontal Vibrations of a Spring-Mass-Damper System

In Figure 3.2, a mass moving in a direction normal to the direction of gravity

is shown. It is assumed that the mass moves without friction. The unstretched

length of the spring is L, and a ﬁxed point O is located at the unstretched po-

sition of the spring, as shown in the ﬁgure. Noting that the spring does not un-

dergo any static deﬂection and carrying out a force balance along the i direc-

tion gives Eq. (3.8) directly. Here, the static-equilibrium position x  0

coincides with the position corresponding to the unstretched spring.

Force Transmitted to Fixed Surface

From Figure 3.1, we see that the total reaction force due to the spring and the

damper on the ﬁxed surface is the sum of the static and dynamic forces. Thus,

(3.9)

Static Dynamic

component component

If we consider only the dynamic part of the reaction force—that is, only those

forces created by the motion x(t) from its static equilibrium position—then

Eq. (3.9) leads to

(3.10)

where x(t) is the solution of Eq. (3.8). Equation (3.10) is used in later chap-

ters to determine the force transmitted to the ground (Section 5.4) or the force

transmitted to the mass when the base is in motion (Sections 5.5 and 6.7).

In the following two examples, we show how to obtain the governing

equation for a system subjected to an external force that has a static component

and how to linearize a system that has a spring with a quadratic nonlinearity.

 c

 kx



 kx  c

3.2 Force Balance and Moment-Balance Methods 73

f(t)

kx kx

FIGURE 3.2

Horizontal vibrations of a spring-

mass-damper system.

⎫

⎬

⎭

⎫

⎬

⎭

EXAMPLE 3.1 Wind-driven oscillations about a system’s static-equilibrium position

In examining wind ﬂow across civil structures such as buildings, water tow-

ers, and lampposts, it has been found

that the wind typically generates a force

on the structure that consists of a steady-state part and a ﬂuctuating part. In

such cases, the excitation force f(t) is represented as

(a)

where f

is the time-independent steady-state force and f

(t) is the ﬂuctuating

time-dependent portion of the force. A single degree-of-freedom model of the

vibrating structure has the form of Eq. (3.8), where x(t) is the displacement of

the structure in the direction of the wind loading and the forcing is given by

Eq. (a); that is,

(b)

We shall determine the static-equilibrium position of this system and

obtain the equation of motion governing oscillations about this static-

equilibrium position. To this end, we assume a solution of the following form

for Eq. (b)

(c)

where x

is determined by the static loading and x

(t) determines motions

about the static position. Thus, after substituting Eq. (c) into Eq. (b) and not-

ing that x

is independent of time, we ﬁnd that

(d)

and that x

(t) is the solution to the equation

(e)

which is the governing equation of motion for oscillations about the static-

equilibrium position .

EXAMPLE 3.2

Eardrum oscillations: nonlinear oscillator

and linearized systems

In this example, we consider a nonlinear oscillator used to study eardrum os-

cillations. We shall determine the static-equilibrium positions of this system

and illustrate how the governing nonlinear equation can be linearized to study

 f

 c

 kx

 f

1t 2

 f

x 1t 2 x

 x

1t 2

 c

 kx  f

 f

1t 2

f 1t2 f

 f

1t 2

74 CHAPTER 3 Single Degree-of-Freedom Systems

E. Naudascher and D. Rockwell, Flow-Induced Vibrations: An Engineering Guide, A. A.

Balkema, Rotterdam, p. 103 (1994).

R. E. Mickens, Oscillations in Planar Dynamic Systems, World Scientiﬁc, Singapore (1996).

3.2 Force Balance and Moment-Balance Methods 75

oscillations local to an equilibrium position. The governing nonlinear equa-

tion has the form

(a)

Quadratic

nonlinearity

The restoring force of the eardrum has a component with a quadratic non-

linearity.

Static-Equilibrium Positions

Noting that there are no external time-dependent forcing terms in this prob-

lem and setting the acceleration term to zero, we ﬁnd that the equilibrium po-

sitions x  x

are solutions of the algebraic equation

(b)

The solutions of Eq. (b) provide us two static-equilibrium positions for the

eardrum, namely,

(c)

Linearization

Next, we substitute

(d)

into Eq. (a) and linearize the nonlinear stiffness term for oscillations about

one of the equilibrium positions in terms of the variable . To this end, we

note that

(e)

In addition,

(f)

Linearized system for “small” amplitude oscillations around x

 0

Making use of Eqs. (e) and (f) in Eq. (a), and noting that x

 x

 0, we ar-

rive at the linear equation

(g)

Linearized system for “small” amplitude oscillations around x

1

Making use of Eqs. (e) and (f) in Eq. (a), and noting that x

 x

1, we

arrive at the linear equation

 kx

 0



 x



d1x

 x



1t 2 1x

 x

1t 22

 x

 2x

1t 2 . . .

1t 2

x1t 2 x

 x

1t 2

1



k1x

 x

2 0

 kx 

 0

⎫

⎬

⎭

(h)

Comparing Eqs. (g) and (h), it is clear that the equations have different stiff-

ness terms.

3.2.2 Moment-Balance Methods

For single degree-of-freedom systems that undergo rotational motion, such as

the system shown in Figure 3.3, the moment balance method is useful in de-

riving the governing equation. A shaft with torsional stiffness k

is attached to

a disc with rotary inertia J

about the axis of rotation, which is directed along

the k direction. An external moment M(t) acts on the disc, which is immersed

in an oil-ﬁlled housing. Let the variable u describe the rotation of the disc, and

let the rotary inertia of the shaft be negligible in comparison to that of the disk.

The principle of angular momentum given by Eq. (1.17) is applied to ob-

tain the equation governing the disc’s motion. First the angular momentum H

of the disc is determined. Since the disk is a rigid body undergoing rotation in

the plane, Eq. (1.20) is used to write the angular momentum about the center

of mass of the disc as

Thus, since the rotary inertia J

and the unit vector k do not change with time,

Eq. (1.17) is rewritten as

(3.11)

where M is the total external moment acting on the free disk. Based on the

free-body diagram shown in Figure 3.3, which also includes the inertial mo-

ment , the governing equation of motion isJ

M  J

k  0

H  J

 kx

 0

76 CHAPTER 3 Single Degree-of-Freedom Systems



Axis of

rotation

M(t)

Shaft with equivalent

torsional stiffness k

Disk with rotary inertia J

about rotation axis

Housing filled with oil

(a) (b)

FIGURE 3.3

(a) A disc undergoing rotational motions and (b) free-body diagram of this disc in the plane normal to the axis of rotation.

M(t)k  k

uk  (3.12)

External moment Restoring moment due Damping moment due Inertial moment

acting on disk to shaft stiffness to oil in housing

After collecting the scalar coefﬁcients of the different vector terms in

Eq. (3.12) and setting them to zero, we arrive at the following scalar equation:

(3.13)

The form of Eq. (3.13) is identical to Eq. (3.8), which was obtained for

a translating vibratory system; that is, the ﬁrst term on the left-hand side is de-

termined by the inertia element J

, the second term on the left-hand side is de-

termined by the damping element c

, the third term on the left-hand side is

determined by the stiffness element k

, and the right-hand side contains the ex-

ternal forcing, the moment M(t). All linear single degree-of-freedom vibra-

tory systems are governed by a linear second-order ordinary differential

equation with an inertia term, a stiffness term, a damping term, and a term

related to the external forcing imposed on the system.

EXAMPLE 3.3

Hand biomechanics

Consider the rotational motion of the hand in the X–Y plane shown in Figure 3.4.

This motion is described by the angle u. An object of mass M is held in the hand,

and the forearm has a mass m and a length l. If we use simpliﬁed models for the

 c

 k

u  M1t 2

 J

k  0c

3.2 Force Balance and Moment-Balance Methods 77

Triceps

Upper arm



Pivot point O

Biceps

Forearm

P. Maróti, L. Berkes, and F. Tölgyesi, Biophysics Problems, Akademiai Kiado, Budapest,

Hungary (1998).

FIGURE 3.4

Hand motion. Source: From P.Maroti, L. Berkes, and F.Tolgyesi, Biophysics Problems: A Text-

L.Berkes, and F.Tolgyesi. Reprinted with permission.

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

forces generated by the muscles, then the biceps provide a force of magnitude

, where k

is a constant, and the triceps provide a force of magnitude

, where K

is a constant and v is the magnitude of the velocity with

which the triceps are stretched. It is further assumed that the forearm can be

treated as a uniform rigid beam. The governing nonlinear equation of motion is

obtained, and following along the lines of Example 3.2, the nonlinear system is

linearized for “small” oscillations about the system equilibrium position.

The equation of motion of the system of Figure 3.4 is derived by carry-

ing out a moment balance about either the center of the forearm or the pivot

point O (the elbow) if the pivot point is a ﬁxed point. Assuming that the pivot

point is a ﬁxed point, Eq. (1.17) is used to carry out a moment balance

about point O. Here, Eq. (1.17) takes the form

(a)

where J

is the rotary inertia of the forearm and the object held in the hand.

The net moment M acting about the point O due to gravity loading and the

forces due to the biceps and triceps is given by

(b)

Therefore, from Eqs. (a) and (b), we ﬁnd that the governing equation takes the

form

(c)

Recognizing that

(d)

and collecting the scalar coefﬁcients of all the vector terms in Eq. (c) and set-

ting them to zero, we obtain the scalar equation

(e)

In this equation, the inertia term is due to the rotary inertia of the forearm

and rotary inertia of the end mass, the damping term is due to the triceps, the

stiffness term is due to the biceps, and there is an additional term due to grav-

ity that makes the equation nonlinear due to the presence of the cos u term.

This latter term inﬂuences the static equilibrium position and the stiffness of

the system, and this inﬂuence depends on the magnitude of u.

Static-Equilibrium Position

Noting that time dependent external moment terms are absent in Eq. (e) and

setting the velocity term and the acceleration term to zero, we ﬁnd that the

equilibrium position u  u

is a solution of the transcendental equation

aM 

 K

 k

au  aM 

bgl cos u  0



 Ml

 K

v  K

k

Mgl cosuk  mg

cos uk  F

ak  F

ak  J

k  0

M Mgl cos uk  mg

cos uk  F

ak  F

M  J

k  0

 K

k

78 CHAPTER 3 Single Degree-of-Freedom Systems

(f)

Linear System Governing “Small” Oscillations about the

Static-Equilibrium Position

We now consider oscillations about the static-equilibrium position and ex-

pand the angular variable u(t) in the form

(g)

and linearize the nonlinear term cos u in Eq. (e). To do this, we carry out the

Taylor-series expansions

of this term and retain only linear terms in This

leads to

(h)

Evaluating the time derivatives of u(t), we ﬁnd that

(i)

On substituting Eqs. (i) and (h) into Eq. (e) and making use of Eq. (f), we

arrive at the following linear equation of motion governing “small” oscilla-

tions of the forearm about the system-equilibrium position:

(j)

where

(k)

It is noted out that the “linear” stiffness of the linearized system is inﬂuenced

by the gravity loading as reﬂected by the second term in k

3.3 NATURAL FREQUENCY AND DAMPING FACTOR

In this section, we deﬁne the natural frequency and damping factor for a vibra-

tory system and explore how these quantities depend on various system prop-

erties. These quantities are discussed without explicitly determining the solu-

tion of the system. They are only a function of the system’s inertia, stiffness,

and damping parameters and independent of the external time-dependent forc-

ing imposed on a system. The solutions for the responses of vibratory systems

represented by Eqs. (3.8) and (3.13), which are discussed in Chapters 4 to 6,

can be characterized in terms of the system’s damping factor.

 k

a  aM 

bgl sin u

aM 

 K

 k

 0

1t 2

 u

2 u

1t 2

1t 2

 u

2 u

1t 2

cos u  cos1u

 u

2 cos u

 u

sin u

 . . .

u1t 2 u

 u

1t 2

 aM 

bgl cos u

 0

3.3 Natural Frequency and Damping Factor 79

T. B. Hildebrand, ibid.