Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

20 CHAPTER 1 Introduction

angle w is used to describe the angular displacement

of the pendulum from the vertical, determine the ab-

solute velocity of the pendulum.

Section 1.2.2

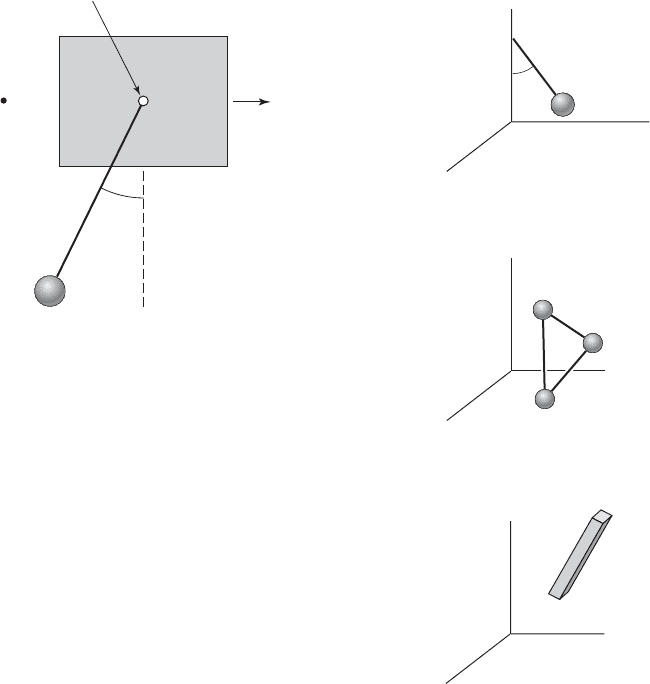
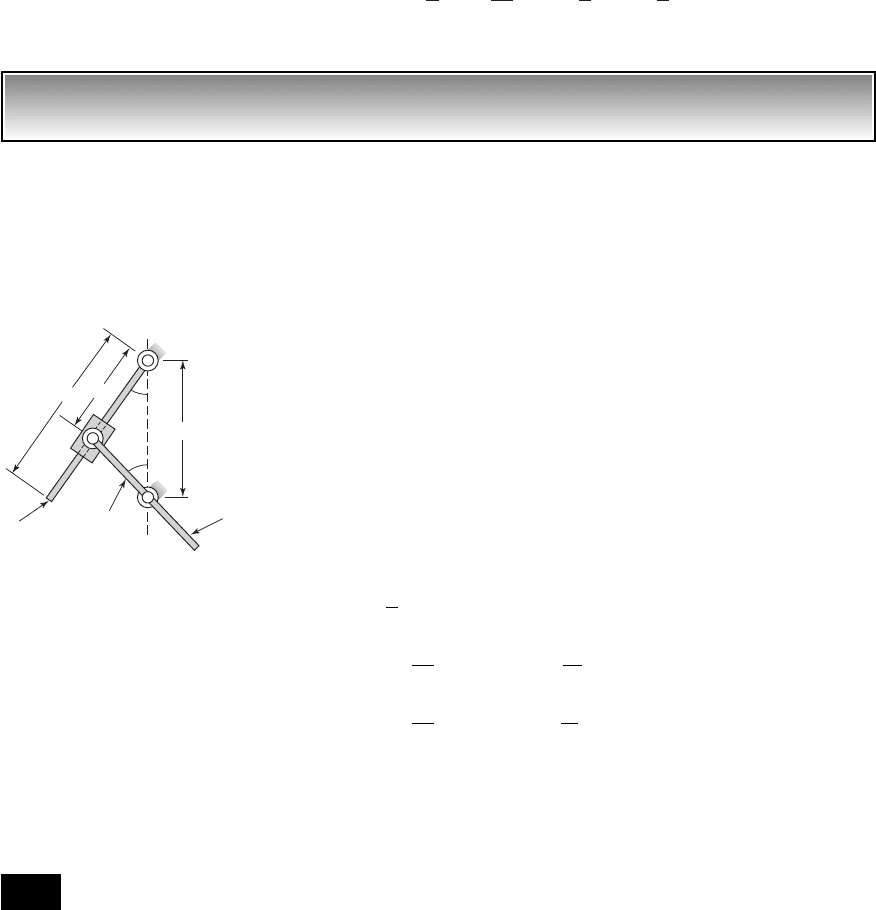
1.7 Determine the number of degrees of freedom for

the systems shown in Figure E1.7. Assume that the

length L of the pendulum shown in Figure E1.7a is con-

stant and that the length between each pair of particles

in Figure E1.7b is constant. Hint: For Figure E1.7c, the

rigid body can be thought of as a system of particles

where the length between each pair of particles is

constant.

Section 1.2.3

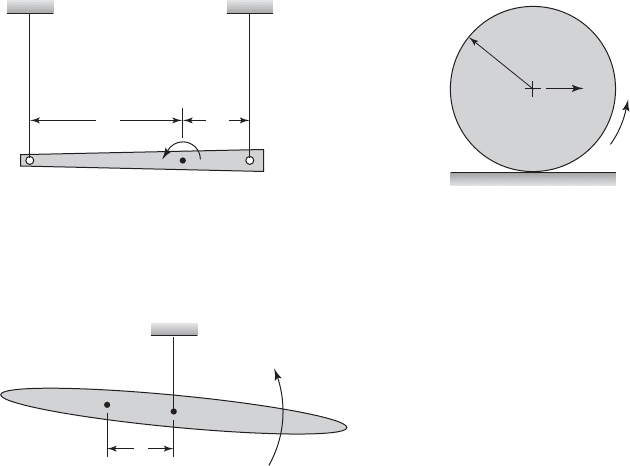
1.8 Draw free-body diagrams for each of the masses

shown in Figure E1.6 and obtain the equations of mo-

tion along the horizontal direction by using Eq. (1.15).

1.9 Draw the free-body diagram for the whole system

shown in Figure E1.6, obtain the system equation of

motion by using Eq. (1.14) along the horizontal direc-

tion, and verify that this equation can be obtained

from Eq. (1.15).

1.10 Determine the linear momentum for the system

shown in Figure E1.5 and discuss if it is conserved.

Assume that the mass of the bar is M

bar

and the dis-

tance from the point O to the center of the bar is L

bar

Pivot, O'



FIGURE E1.6

, y

, z

)



(b) System of three particles

(a) Spherical pendulum

FIGURE E1.7

1.11 Determine the angular momentum of the system

shown in Figure 1.6 about the point O and discuss if

it is conserved.

1.12 A rigid body is suspended from the ceiling by

two elastic cables that are attached to the body at the

points O and O, as shown in Figure E1.12. Point G

is the center of mass of the body. Which of these

points would you choose to carry out an angular-

momentum balance based on Eq. (1.17)?

1.13 Consider the rigid body shown in Figure E1.13.

This body has a mass m and rotary inertia J

about the

Exercises 21

center of mass G. It is suspended from a point O on

the ceiling by using an elastic suspension. The point

of attachment O is at a distance l from the center of

mass G of this body. M(t) is an external moment ap-

plied to the system along an axis normal to the plane

of the body. Use the generalized coordinates x, which

describes the up and down motions of point O from

point O, and u, which describes the angular oscilla-

tions about an axis normal to the plane of the rigid

body. For the system shown in Figure E1.13, use the

principle of angular-momentum balance given by

Eq. (1.17) and obtain an equation of motion for the

system. Assume that gravity loading is present.

Section 1.2.4

1.14 For the system shown in Figure E1.13, construct

the system kinetic energy.

1.15 Determine the kinetic energy of the planar pen-

dulum of Example 1.1.

1.16 Consider the disc rolling along a line in Fig-

ure E1.16. The disc has a mass m and a rotary inertia

about the center of mass G. Answer the following:

(a) How many degrees of freedom does this system

have? and (b) Determine the kinetic energy for this

system.

1.17 In the system shown in Figure 1.6, if the mass of

the pendulum is m, the length of the pendulum is r,

and the rotary inertia of the disc about the point O is

, determine the system kinetic energy.

1.18 Referring to Figure E1.6 and assuming that the

bar to which the pendulum mass m is connected is

massless, determine the kinetic energy for the system.

1.19 Determine the kinetic energy of the system

shown in Figure E1.5.

m, J

O' O"



FIGURE E1.12

M(t)

m, J

FIGURE E1.13

m, J



FIGURE E1.16

Components of vibrating systems: an air spring and a steel helical spring. (Source: Courtesy of Enidine Incorporated; Stockxpert.com.)

2323

Modeling of Vibratory Systems

2.1 INTRODUCTION

2.2 INERTIA ELEMENTS

2.3 STIFFNESS ELEMENTS

2.3.1 Introduction

2.3.2 Linear Springs

2.3.3 Nonlinear Springs

2.3.4 Other Forms of Potential Energy Elements

2.4 DISSIPATION ELEMENTS

2.4.1 Viscous Damping

2.4.2 Other Forms of Dissipation

2.5 MODEL CONSTRUCTION

2.5.1 Introduction

2.5.2 A Microelectromechanical System

2.5.3 The Human Body

2.5.4 A Ski

2.5.5 Cutting Process

2.6 DESIGN FOR VIBRATION

2.7 SUMMARY

EXERCISES

2.1 INTRODUCTION

In this chapter, the elements that comprise a vibratory system model are de-

scribed and the use of these elements to construct models is illustrated with

examples. There are, in general, three elements that comprise a vibrating sys-

tem: i) inertia elements, ii) stiffness elements, and iii) dissipation elements. In

addition to these elements, one must also consider externally applied forces

and moments and external disturbances from prescribed initial displacements

and/or initial velocities.

The inertia element stores and releases kinetic energy, the stiffness ele-

ment stores and releases potential energy, and the dissipation or damping

element is used to express energy loss in a system. Each of these elements has

different excitation-response characteristics and the excitation is in the form

of either a force or a moment and the corresponding response of the element

is in the form of a displacement, velocity, or acceleration. The inertia ele-

ments are characterized by a relationship between an applied force (or mo-

ment) and the corresponding acceleration response. The stiffness elements

are characterized by a relationship between an applied force (or moment)

and the corresponding displacement (or rotation) response. The dissipation

elements are characterized by a relationship between an applied force (or mo-

ment) and the corresponding velocity response. The nature of these relation-

ships, which can be linear or nonlinear, are presented in this chapter. The units

associated with these elements and the commonly used symbols for the dif-

ferent elements are shown in Table 2.1.

In this chapter, we shall show how to:

• Compute the mass moment of inertia of rotational systems.

• Determine the stiffness of various linear and nonlinear elastic components

in translation and torsion and the equivalent stiffness when many individ-

ual linear components are combined.

• Determine the stiffness of ﬂuid, gas, and pendulum elements.

• Determine the potential energy of stiffness elements.

• Determine the damping for systems that have different sources of dissipa-

tion: viscosity, dry friction, ﬂuid, and material.

• Construct models of vibratory systems.

2.2 INERTIA ELEMENTS

Translational motion of a mass is described as motion along the path followed

by the center of mass. The associated inertia property depends only on the to-

tal mass of the system and is independent of the geometry of the mass distri-

bution of the system. The inertia property of a mass undergoing rotational

motions, however, is a function of the mass distribution, speciﬁcally the mass

moment of inertia, which is usually deﬁned about its center of mass or a ﬁxed

point O. When the mass oscillates about a ﬁxed point O or a pivot point O, the

rotary inertia J

is given by

24 CHAPTER 2 Modeling of Vibratory Systems

TABLE 2.1

Units of Components Comprising a

Vibrating Mechanical System and

Their Customary Symbols

Quantity Units

Translational motion

Mass, m kg

Stiffness, k N

Damping, c Ns

External force, F N

Rotational motion

Mass moment of inertia, J kgm

Stiffness, k

Nm/rad

Damping, c

Nms/rad

External moment, M Nm

(2.1)

where m is the mass of the element, J

is the mass moment of inertia about

the center of mass, and d is the distance from the center of gravity to the

point O. In Eq. (2.1), the mass moments of inertia J

and J

are both deﬁned

with respect to axes normal to the plane of the mass. This relationship be-

tween the mass moment of inertia about an axis through the center of mass G

and a parallel axis through another point O follows from the parallel-axes

theorem. The mass moments of inertia of some common shapes are given in

Table 2.2.

The questions of how the inertia properties are related to forces and mo-

ments and how these properties affect the kinetic energy of a system are ex-

amined next. In Figure 2.1, a mass m translating with a velocity of magnitude

in the X-Y plane is shown. The direction of the velocity vector is also shown

in the ﬁgure, along with the direction of the force acting on this mass.

In stating the principles of linear momentum and angular momentum in

Chapter 1, certain relationships between inertia properties and forces and

moments were assumed. These relationships are revisited here. Based on the

principle of linear momentum, which is given by Eq. (1.11), the equation

governing the motion of the mass is

which, when m and i are independent of time, simpliﬁes to

(2.2)

On examining Eq. (2.2), it is evident that for translational motion, the inertia

property m is the ratio of the force to the acceleration. The units for mass

F  mx

Fi 

1mx

 J

 md

2.2 Inertia Elements 25

TABLE 2.2

Mass Moments of Inertia about

Axis z Normal to the

x-y Plane and Passing Through

the Center of Mass

L/2

Slender bar



Circular disk

Sphere

Circular cylinder

 J

 m A3R

 h

 mR

FIGURE 2.1

Mass in translation.

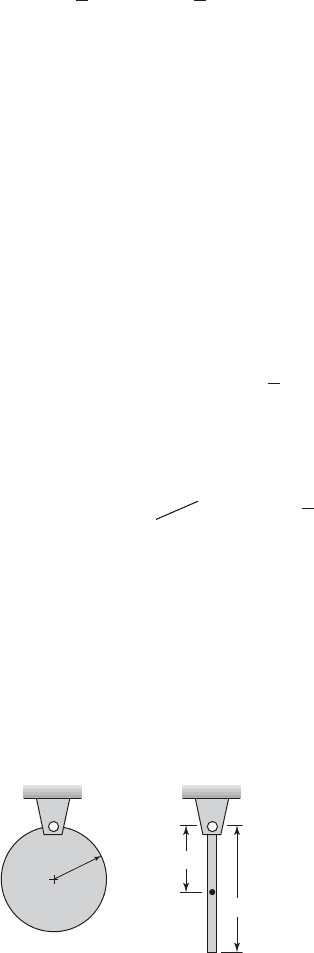
shown in Table 2.1 should also be evident from Eq. (2.2). From Eq. (1.22), it

follows that the kinetic energy of mass m is given by

(2.3)

and we have used the identity i  i  1. From the deﬁnition given by Eq. (2.3),

it is clear that the kinetic energy of translational motion is linearly proportional

to the mass. Furthermore, the kinetic energy is proportional to the second power

of the velocity magnitude. To arrive at Eq. (2.3) in a different manner, let us con-

sider the work-energy theorem discussed in Section 1.2.4. We assume that the

mass shown in Figure 2.1 is translated from an initial rest state, where the ve-

locity is zero at time t

, to the ﬁnal state at time t

. Then, it follows from

Eq. (1.26) that the work W done under the action of a force Fi is

(2.4)

where we have used the relation dx  dt. Hence, the kinetic energy is

(2.5)

which is identical to Eq. (2.3).

For a rigid body undergoing only rotation in the plane with an angular

speed , one can show from the principle of angular momentum discussed in

Section 1.2.3 that

(2.6)

where M is the moment acting about the center of mass G or a ﬁxed point O (as

shown in Figure 2.2) along the direction normal to the plane of motion and J is

M  Ju

T1t  t

2 T1t  t

0

 W 





dt 





W 



dxi 



dxi 



T 

m1x

i2

26 CHAPTER 2 Modeling of Vibratory Systems

L/2

c.g.

m, J

(b)(a)

FIGURE 2.2

(a) Uniform disk hinged at a point on its perimeter and (b) bar of uniform mass hinged

at one end.

the associated mass moment of inertia. From Eq. (2.6), it follows that for rota-

tional motion, the inertia property J is the ratio of the moment to the angular

acceleration. Again, one can verify that the units of J shown in Table 2.1 are

consistent with Eq. (2.6). This inertia property is also referred to as rotary in-

ertia. Furthermore, to determine how the inertia property J affects the kinetic

energy, we use Eq. (1.25) to show that the kinetic energy of the system is

(2.7)

Hence, the kinetic energy of rotational motion only islinearly proportional

to the inertia property J, the mass moment of inertia. Furthermore, the ki-

netic energy is proportional to the second power of the angular velocity

magnitude.

In the discussions of the inertia properties of vibratory systems provided

thus far, the inertia properties are assumed to be independent of the dis-

placement of the motion. This assumption is not valid for all physical sys-

tems. For a slider mechanism discussed in Example 2.2, the inertia property

is a function of the angular displacement. Other examples can also be found

in the literature.

EXAMPLE 2.1 Determination of mass moments of inertia

We shall illustrate how the mass moments of inertia of several different rigid

body distributions are determined.

Uniform Disk

Consider the uniform disk shown in Figure 2.2a. If J

is the mass moment of

inertia about the disk’s center, then from Table 2.2

and, therefore, the mass moment of inertia about the point O, which is located

a distance R from point G,is

(a)

Uniform Bar

A bar of length L is suspended as shown in Figure 2.2b. The bar’s mass is uni-

formly distributed along its length. Then the center of gravity of the bar is lo-

cated at L/2. From Table 2.2, we have that



 J

 mR



 mR



T 

2.2 Inertia Elements 27

J. P. Den Hartog, Mechanical Vibrations, Dover, NY, p. 352 (1985).

and therefore, after making use of the parallel axis theorem, the mass moment

of inertia about the point O is

(b)

EXAMPLE 2.2

Slider mechanism: system with varying inertia property

In Figure 2.3, a slider mechanism with a pivot at point O is shown. A slider of

mass m

slides along a uniform bar of mass m

. Another bar, which is pivoted

at point O, has a portion of length b that has a mass m

and another portion

of length e that has a mass m

. We shall determine the rotary inertia J

of this

system and show its dependence on the angular displacement coordinate w.

If a

is the distance from the midpoint of bar of mass m

to O and a

is the

distance from the midpoint of bar of mass m

to O, then from geometry we

ﬁnd that

(a)

and hence, all motions of the system can be described in terms of the angular

coordinate w. The rotary inertia J

of this system is given by

(b)

where

(c)

In arriving at Eqs. (b) and (c), the parallel-axes theorem has been used in de-

termining the bar inertias J

, J

, and J

. From Eqs. (b) and (c), it is clear that

the rotary inertia J

of this system is a function of the angular displacement w.

2.3 STIFFNESS ELEMENTS

2.3.1 Introduction

Stiffness elements are manufactured from different materials and they have

many different shapes. One chooses the type of element depending on the re-

quirements; for example, to minimize vibration transmission from machinery

1w 2 m

 m

 m

 a

 ae cos1p  w2d

1w 2 m

 m

 m

 a

 ab cos w d



1w 2 m

1w 2

 J

 J

1w 2 J

1w 2

1w 2 1e/22

 a

 ae cos 1p  w2

1w 2 1b/22

 a

 ab cos w

1w 2 a

 b

 2ab cos w

 J

 m a







28 CHAPTER 2 Modeling of Vibratory Systems





FIGURE 2.3

Slider mechanism.

to the supporting structure, to isolate a building from earthquakes, or to

absorb energy from systems subjected to impacts. Some representative types

of stiffness elements that are commercially available are shown in Figure 2.4

along with their typical application.

The stiffness elements store and release the potential energy of a system.

To examine how the potential energy is deﬁned, let us consider the illustra-

tion shown in Figure 2.5, in which a spring is held ﬁxed at end O, and at the

other end, a force of magnitude F is directed along the direction of the unit

vector j. Under the action of this force, let the element stretch from an initial

or unstretched length L

to a length L

 x along the direction of j. In under-

going this deformation, the relationship between F and x can be linear or non-

linear as discussed subsequently.

2.3 Stiffness Elements 29

FIGURE 2.4

(a) Building or highway base isolation for lateral motion using cylindrical rubber bearings; (b) wire rope isolators

to isolate vertical motions of machinery; (c) air springs used in suspension systems to isolate vertical motions;

(d) typical steel coil springs for isolation of vertical motions; and (e) steel cable springs used in a chimney tuned

mass damper to suppress lateral motions. Source: Holmes Consulting Group; Wire Rope Catalogue, pg. 6, Enidine

Incorporated, 2006; http://www.enidine.com /Airsprings.html 2006 Enidine Incorporated; Figures of Series C Vibro

Isolators http://www.isolationtech.com/sercw.htm; Figure of Tuned Mass Damper http://www.iesysinc.com/

Tuned_Mass_Dampers.php 2001–2002 Industrial Environmental Sysytems Inc.

(a) (b)

Motion

Cable

springs

Motion

Wire rope

Spring

Springs