Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

EXAMPLE 1.3 Kinematics of a particle in a rotating frame

A particle is free to move in a plane, which rotates about an axis normal to the

plane as shown in Figure 1.5. The unit vectors i and j, which point along the

X and Y directions, respectively, have ﬁxed directions for all time. We shall be

determining the velocity of the particle P located in the x-y plane. The x-y-z

frame rotates with respect to the X-Y-Z frame, which is ﬁxed in time. The ro-

tation takes place about the z-axis with an angular speed v. The unit vector k

is oriented along the axis of rotation, which points along the z direction. The

unit vectors e

and e

are ﬁxed to the rotating frame, and they point along the

x and y directions, respectively.

In the rotating frame, the position vector from the ﬁxed point O to the

point P is

(a)

Making use of the ﬁrst of Eqs. (1.2) for the velocity of a particle, noting

Eqs. (1.8), recognizing that and making use of Eqs. (d) of Exam-

ple 1.1, the velocity of the particle is

(b) 1x

 vy

 1y

 vx

 x

 x

 y

v 



2

V  vk,

r  x

 y

10 CHAPTER 1 Introduction

In Chapters 7 and 8, the particle kinematics discussed here will be used in examining vibrations

of a gyro-sensor.



, y

,0)

FIGURE 1.5

Particle in a rotating frame.

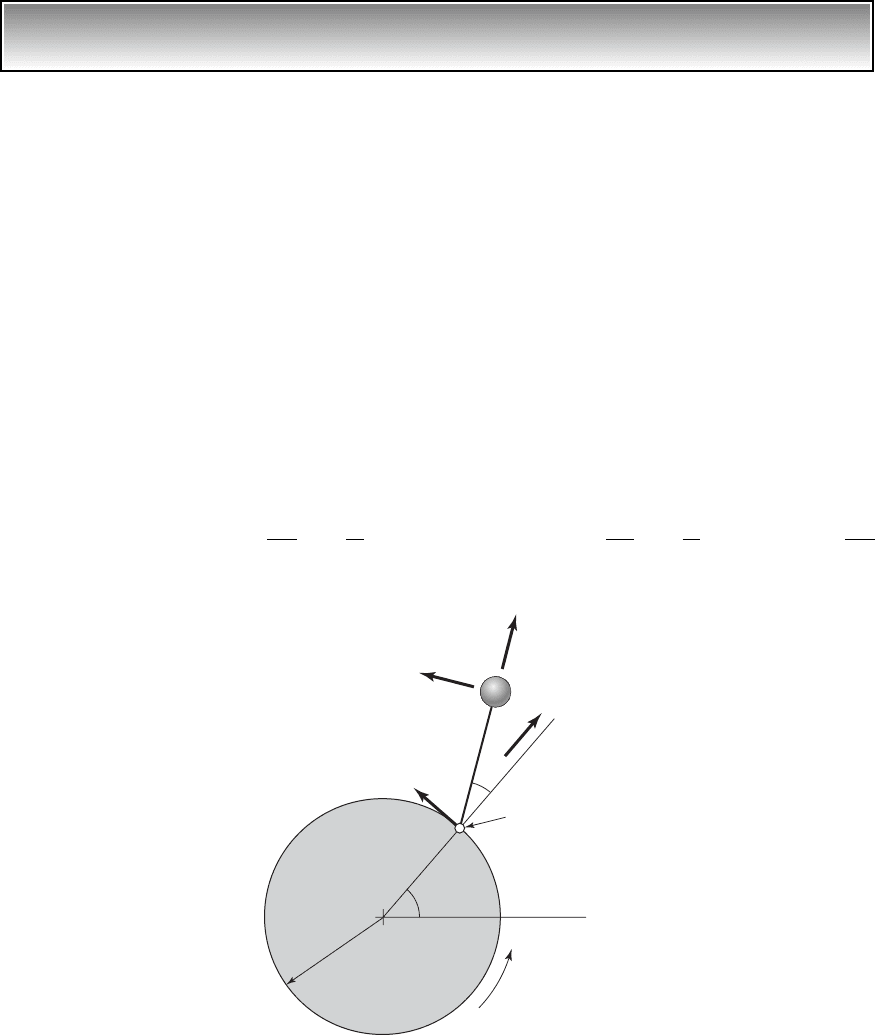
EXAMPLE 1.4 Absolute velocity of a pendulum attached to a rotating disc

We shall determine the absolute velocity of the pendulum attached to the ro-

tating disc shown in Figure 1.6. This system is representative of a centrifugal

pendulum absorber treated in Chapter 8. Assume that the point O is ﬁxed in

an inertial reference frame, the unit vectors and are ﬁxed to the pendu-

lum, and that the orthogonal unit vectors and are ﬁxed to the rotating

disc. The motions of the pendulum are restricted to the plane containing the

unit vectors and , the angle u describes the rotation of the disc with re-

spect to the horizontal, and the angle w describes the position of the pendu-

lum relative to the disc.

From the ﬁgure, we see that the position vector describing the location of

the mass m is

Then, the velocity of mass m is



 e¿

1R  r cosw2 1R  r cosw2

de¿

 e¿

1r sinw2 r sinw

de¿

 1R  r cosw2e¿

 r sinwe¿

 Re¿

 r coswe¿

 r sinwe¿

 Re¿

 re

e¿

1.2 Preliminaries from Dynamics 11

Pivot





FIGURE 1.6

Pendulum attached to a rotating disc.

Since the orientation of the unit vectors and change with time due to the

rotation of the disc, we have

which leads to

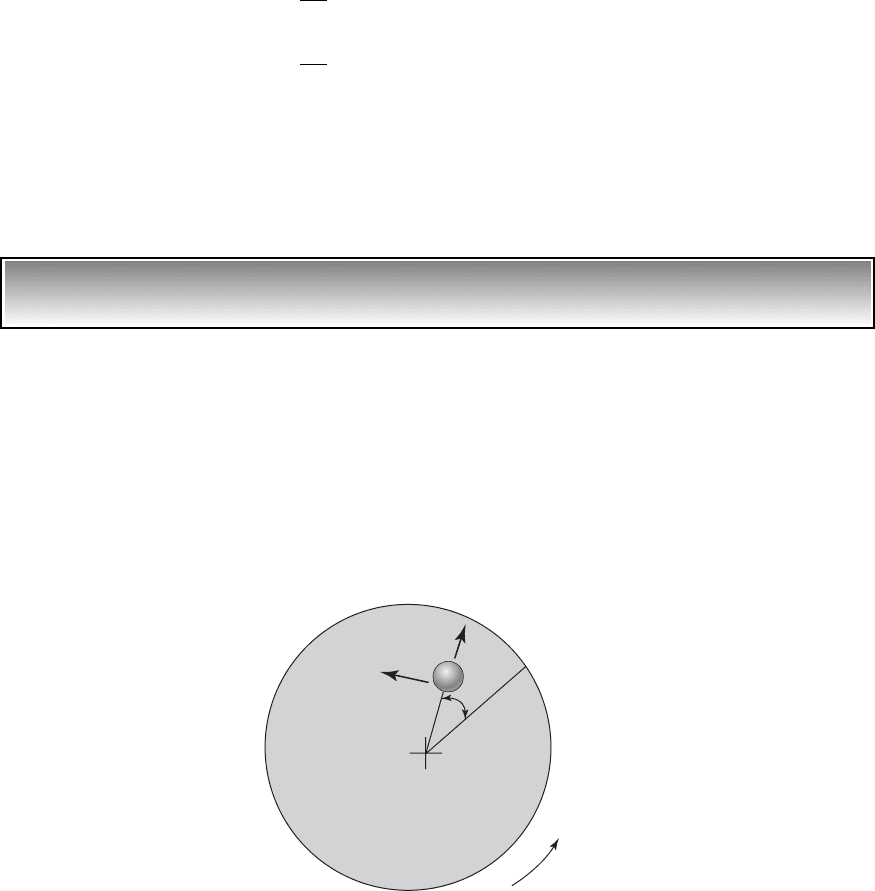
EXAMPLE 1.5

Moving mass on a rotating table

Consider a mass m that is held by elastic constraints and is located on a table

that is rotating at a constant speed v, as shown in Figure 1.7. We shall deter-

mine the absolute velocity of the mass. We assume that point O is ﬁxed in the

vertical plane, that the unit vectors and are ﬁxed to the mass m, as shown

in Figure 1.7, and that . Then

and the velocity is given by

 re

k  e

 e

r 1w

 u

2sin we¿

 1Ru

 r1w

 u

2cos w2e¿

rw

sin we¿

 1R  r cos w2u

e¿

 rw

cos we¿

 ru

sin we¿

de¿

 V  e¿

 u

k  e¿

u

e¿

de¿

 V  e¿

 u

k  e¿

 u

e¿

12 CHAPTER 1 Introduction

N. S. Clarke, “The Effect of Rotation upon the Natural Frequencies of a Mass-Spring System,”

J. Sound Vibration, 250(5), pp. 849–887 (2000).





FIGURE 1.7

Frictionless rotating table of radius L on which mass m is elastically constrained.

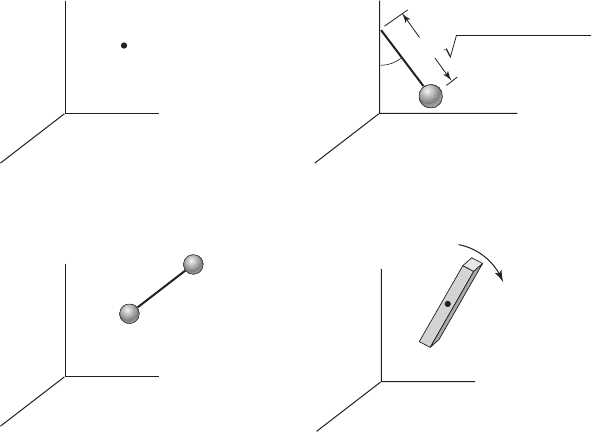
1.2.2 Generalized Coordinates and Degrees of Freedom

To describe the physical motion of a system, one needs to choose a set of vari-

ables or coordinates, which are referred to as generalized coordinates.

They

are commonly represented by the symbol q

The motion of a free particle, which is shown in Figure 1.8a, is described

by using the generalized coordinates q

 x

, q

 y

, and q

 z

. Here, all

three of these coordinates are needed to describe the motion of the system.

The minimum number of independent coordinates needed to describe the mo-

tion of a system is called the degrees of freedom of a system. Any free parti-

cle in space has three degrees of freedom.

In Figure 1.8b, a planar pendulum is shown. The pivot point of this

pendulum is ﬁxed at (x

,0) and the pendulum has a constant length L.

For this case, the coordinates are chosen as x

and y

. However, since the pen-

dulum length is constant, these coordinates are not independent of each other

because

(1.9)

Equation (1.9) is an example of a constraint equation, which in this case is a

geometric constraint.

The motion of the pendulum in the plane can be

described by using either x

or y

. Since x

 L sin u and y

 L  L cos u,

one can also use the variable u to describe the motion of the pendulum,

which is an independent coordinate that qualiﬁes as a generalized coordinate.

Since only one independent variable or coordinate is needed to describe the

pendulum’s motion, a planar pendulum of constant length has one degree of

freedom.

As a third example, a dumbbell in the plane is considered in Figure 1.8c.

In this system of particles, a massless rod of constant length connects two

particles. Here, the coordinates are chosen as x

, y

, x

, and y

, where this

 x

 1y

 y

 L

 r

 r1v  u

 r

 r1v  u

2k  e

 r

 r



3re

1.2 Preliminaries from Dynamics 13

In a broader context, the term “generalized coordinates” is also used to refer to any set of pa-

rameters that can be used to specify the system conﬁguration. There are subtle distinctions in the

deﬁnitions of generalized coordinates used in the literature. Here, we refer to the generalized

coordinates as the coordinates that form the minimum set or the smallest possible number of

variables needed to describe a system (J. L. Synge and B. A. Grifﬁth, Principles of Mechanics,

Section 10.6, McGraw Hill, New York, 1959).

A geometric constraint is an example of a holonomic constraint, which can be expressed in the

form f(q

, q

,...,q

; t)  0, where q

are the generalized coordinates and t is time.

set includes the coordinates of each of the two particles in the plane. Since

the length of the dumbbell is constant, only three of these coordinates are

independent. A minimum of three of the four coordinates is needed to de-

scribe the motion of the dumbbell in the plane. Hence, a dumbbell in the plane

has three degrees of freedom. The generalized coordinates in this case are

chosen as x

, y

, and u, where x

and y

are the coordinates of the center of

mass of the dumbbell and u represents the rotation about an axis normal to the

plane of the dumbbell.

In Figure 1.8d, a rigid body that is free to move in the X–Y plane is shown.

The generalized coordinates q

 x

and q

 y

specify the translation of the

center of mass of the rigid body. Apart from these two generalized coordi-

nates, another generalized coordinate u, which represents the rotation about

the Z-axis, is also needed. Hence, a rigid body that is free to move in the plane

has three degrees of freedom. It is not surprising that the dumbbell in the

plane has the same number of degrees of freedom as the rigid body shown in

Figure 1.8d, since the collection of two particles, which are a ﬁxed distance L

apart in Figure 1.8c, is a rigid body.

In the examples shown in Figures 1.8b and 1.8c, one needed to take into

account the constraint equations in determining the number of degrees of

freedom of a system. For a system conﬁguration speciﬁed by n coordinates,

14 CHAPTER 1 Introduction

, y

, z

)

, y

,0)

, y

,0)

, y

,0)

, y

,0)

, y

,0)

 x

)

 (y

 y

)

L 



(a)

(c)

(b)

(d)

FIGURE 1.8

(a) Free particle in space; (b) planar pendulum; (c) dumbbell in plane; and (d) free rigid body

in plane.

which are related by m independent constraints, the number of degrees of

freedom N is given by

(1.10)

The dynamics of vibratory systems with a single degree of freedom is

treated in Chapters 3 through 6, the dynamics of vibratory systems with

ﬁnite but more than one degree of freedom is treated in Chapters 7 and 8, and

the dynamics of vibratory systems with inﬁnite number of degrees of freedom

is treated in Chapter 9. For much of the material presented in these chapters,

the physical systems move in the plane and the systems are subjected only to

geometric constraints.

1.2.3 Particle and Rigid-Body Dynamics

In the previous two subsections, it was shown how one can determine the

velocities and accelerations of particles and rigid bodies and the number of

independent coordinates needed to describe the motion of a system. Here, a

discussion of the physical laws governing the motion of a system is presented.

The velocities and accelerations determined from kinematics will be used in

applying these laws to a system.

For all systems treated in this book, the speeds at which the systems

travel will be much less than the speed of light. In the area of mechanics, the

dynamics of such systems are treated under the area broadly referred to as

Newtonian Mechanics. Two important principles that are used in this area are

the principle of linear momentum and the principle of angular momentum,

which are due to Newton and Euler, respectively.

Principle of Linear Momentum

The Newtonian principle of linear momentum states that in an inertial refer-

ence frame, the rate of change of the linear momentum of a system is equal to

the total force acting on this system. This principle is stated as

(1.11)

where F represents the total force vector acting on the system and p represents

the total linear momentum of the system. Again, it is important to note that

the time derivative in Eq. (1.11) is deﬁned in an inertial reference frame and

that the linear momentum is constructed based on the absolute velocity of the

system of interest.

Particle Dynamics

For a particle, the linear momentum is given by

p  mv (1.12)

where m is the mass of the particle and v is the absolute velocity of the parti-

cle. When the mass m is constant, Eq. (1.11) takes the familiar form

F 

N  n  m

1.2 Preliminaries from Dynamics 15

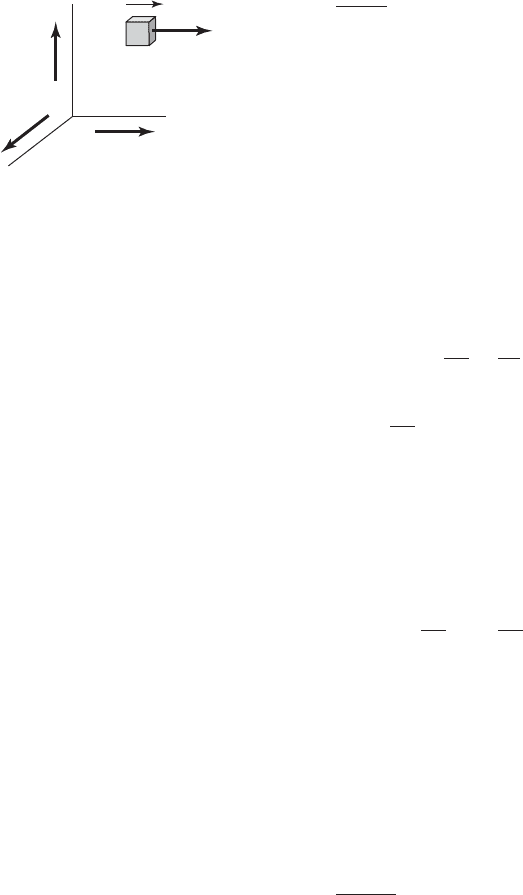
(1.13)

which is referred to as Newton’s second law of motion. The velocity in

Eq. (1.12) and the acceleration in Eq. (1.13) are determined from kinematics.

Therefore, for the particle shown in Figure 1.9, it follows from Eq. (1.13) that

Dynamics of a System of n Particles

For a system of n particles, the principle of linear momentum is written as

(1.14)

where the subscript i refers to the ith particle in the collection of n particles,

is the external force acting on particle i, p

is the linear momentum of this

particle, m

is the constant mass of the ith particle, and v

is the absolute ve-

locity of the ith particle. For the jth particle in this collection, the governing

equation takes the form

(1.15)

where F

is the internal force acting on particle j due to particle i. Note that

in going from the equation of motion for an individual particle given by

Eq. (1.15) to that for a system of particles given by Eq. (1.14), it is assumed

that all of the internal forces satisfy Newton’s third law of motion; that is, the

assumption of equal and opposite internal forces .

If the center of mass of the system of particles is located at point G, then

Eq. (1.14) can be shown to be equivalent to

(1.16)

where m is the total mass of the system and v

is the absolute velocity of the

center of mass of the system. Equation (1.16) is also valid for a rigid body.

It is clear from Eq. (1.11) that in the absence of external forces, the lin-

ear momentum of the system is conserved; that is, the linear momentum of the

system is constant for all time. This is an important conservation theorem,

which is used, when applicable, to examine the results obtained from analy-

sis of vibratory models.

F 

d1mv

F



i 1

i j



 m



i 1

F 

i1



i1



F  mx

Fi  mx

F 

d1mv 2

 ma

16 CHAPTER 1 Introduction

FIGURE 1.9

Free particle of mass m translating

along the i direction.

1.2 Preliminaries from Dynamics 17

Principle of Angular Momentum

The principle of angular momentum states that the rate of change of the an-

gular momentum of a system with respect to the center of mass of the system

or a ﬁxed point is equal to the total moment about this point. This principle is

stated as

(1.17)

where the time derivative is evaluated in an inertial reference frame, M is the

net moment acting about a ﬁxed point O in an inertial reference frame or

about the center of mass G, and H is the total angular momentum of the sys-

tem about this point.

For a particle, the angular momentum is given by

(1.18)

where r is the position vector from the ﬁxed point O to the particle and p is

the linear momentum of this particle based on the absolute velocity of this

particle. For a system of n particles, the principle given by Eq. (1.17) can be

applied with respect to either the center of mass G of the system or a ﬁxed

point O. The angular momentum takes the form

(1.19)

where r

is the position vector from either point O or point G to the ith parti-

cle and p

is the linear momentum of the particle based on the absolute veloc-

ity of the particle. For a rigid body moving in the plane as in Figure 1.8d, the

angular momentum about the center of mass is given by

(1.20)

where J

is the mass moment of inertia about the center of mass and the unit

vector k points along the Z-direction. The angular momentum of the rigid

body about the ﬁxed point O is given by

(1.21)

where J

is the mass moment of inertia about the ﬁxed point.

From Eq. (1.17), it is clear that in the absence of external moments, the

angular momentum of the system is conserved; that is, the angular momen-

tum of the system is constant for all time. This is another important conserva-

tion theorem, which is used, when applicable, to examine the results obtained

from analysis of vibratory models.

The governing equations derived for vibratory systems in the subsequent

chapters are based on Eqs. (1.11) and (1.17). Speciﬁc examples are not pro-

vided here, but the material provided in later chapters are illustrative of how

these important principles are used for developing mathematical models of a

system.

 J

H 

i1



i1

 p

H  r  p

M 

18 CHAPTER 1 Introduction

1.2.4 Work and Energy

The deﬁnition for kinetic energy T of a system is provided and the relation be-

tween work done on a system and kinetic energy is presented. The kinetic en-

ergy of a system is a scalar quantity. For a system of n particles, the kinetic

energy is deﬁned as

(1.22)

where v

is the absolute velocity of the ith particle and the “” symbol is the

scalar dot product of two vectors.

For a rigid body, the kinetic energy is written in the following convenient

form, which is due to König,

(1.23)

where the ﬁrst term on the right-hand side represents the kinetic energy asso-

ciated with the translation of the system and the second term on the right-hand

side represents the kinetic energy associated with rotation about the center

of mass of the system. For a rigid body moving in the plane as shown in Fig-

ure 1.8d, the kinetic energy takes the form

(1.24)

where the ﬁrst term on the right-hand side is the translational part based on

the velocity v

of the center of mass of the system and the second term on the

right-hand side is associated with rotation about an axis, which passes

through the center of mass and is normal to the plane of motion. For a rigid

body rotating in the plane about a ﬁxed point O, the kinetic energy is deter-

mined from

(1.25)

Work-Energy Theorem

According to the work-energy theorem, the work done in moving a system

from a point A to point B is equal to the change in kinetic energy of the sys-

tem, which is stated as

(1.26)

where W

is the work done in moving the system from the initial point A to

the ﬁnal point B, T

is the kinetic energy of the system at point B, and T

the kinetic energy of the system at point A. The work done W

is a scalar

quantity.

 T

 T

T 

m 1v

2

T  T

1translational2

 T

1rotational2

T 

i 1

2

i 1

D. T. Greenwood, Principles of Dynamics, Prentice Hall, Upper Saddle River, NJ, Chapter 4

(1988).

Exercises 19

EXERCISES

Section 1.1

1.1 Choose any two contributors from Table 1.1,

study their contributions, and write a paragraph about

each of them.

Section 1.2.1

1.2 Consider the planar pendulum kinematics dis-

cussed in Example 1.1, start with position vector

resolved in terms the unit vectors i and j, and verify

the expressions obtained for the acceleration and ve-

locity given by Eq. (f) of Example 1.1.

1.3 Consider the kinematics of the rolling disc con-

sidered in Example 1.2, and verify that the instanta-

neous acceleration of the point of contact is not zero.

1.4 Show that the acceleration of the particle in the ro-

tating frame of Example 1.3 is

where a is the magnitude of the angular acceleration

of the rotating frame about the z axis.

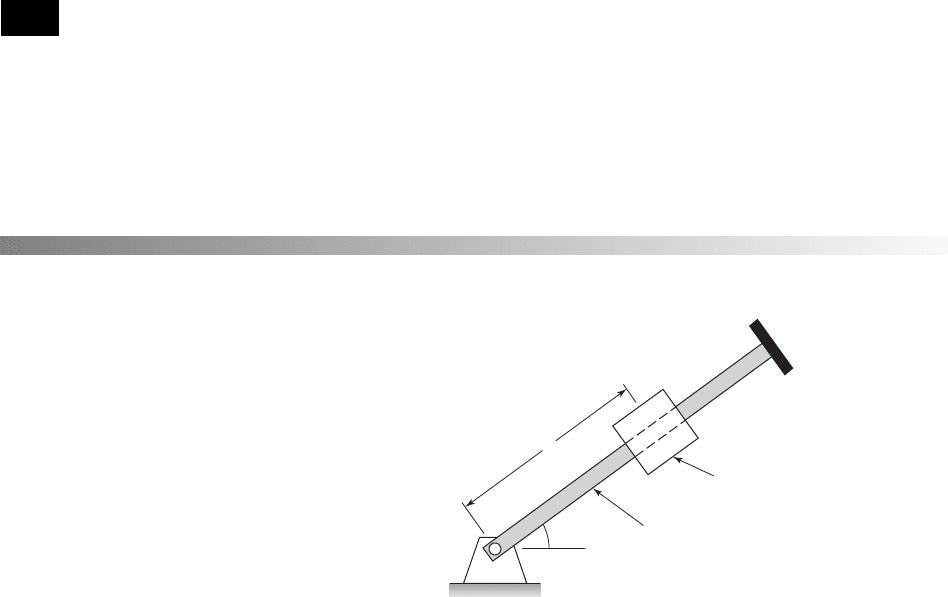
1.5 In Figure E1.5, a slider of mass M

is located on a

bar whose angular displacement in the plane is descri-

bed by the coordinate u. The motion of the slider from

 2vx

 v

 ax

a  1x

 2vy

 v

 ay



P/O

the pivot point is measured by the coordinate r

. The

acceleration due to gravity acts in a direction normal

to the plane of motion. Assume that the point O is

ﬁxed in an inertial reference frame and determine the

absolute velocity and absolute acceleration of the

slider.

1.6 Consider the pendulum of mass m attached to a

moving pivot shown in Figure E1.6. Assume that the

pivot point cannot translate in the vertical direction. If

the horizontal translation of the pivot point from the

ﬁxed point O is measured by the coordinate x and the

Bar of rotary

inertia J

Slider of mass M

(t)

FIGURE E1.5

Another form of energy called potential energy of a system is addressed

in Chapter 2. Speciﬁc examples are not provided here, but the use of kinetic

energy and work done in developing mathematical models of vibratory sys-

tems is illustrated in the subsequent chapters.

1.3 SUMMARY

In this chapter, a review from dynamics has been presented in the spirit of

summarizing material that is typically a prerequisite to the study of vibra-

tions. In carrying out this discussion, attention has been paid to kinematics,

the notion of degree of freedom, and the principles of linear and angular mo-

mentum. This background material provides a summary of the foundation for

the material presented in the subsequent chapters.