Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


The results obtained from Eq. (9.163), which is for the case of a mass di-
rectly attached to the beam, are shown in Figures 9.24 to 9.26 for e 2.5%
and for e 5%. It is seen that in order to keep the error below 5% one must
use a mass ratio of 2.5 when the mass is located at the free end of a cantilever
beam. When the mass is placed at the midpoint of a clamped-clamped beam,
610 CHAPTER 9 Vibrations of Beams
0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
10
20
30
40
50
60
M
so
K
s
200, 2.5%
K
s
200, 5%
K
s
50, 2.5%
K
s
50, 5%
1
0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
0
10
20
30
40
50
60
M
so
2.5%
5%
1
FIGURE 9.23
Values of M
so
for a cantilever beam
carrying a single degree-of-freedom
system at h
1
for which the error is
less than 5% and less than 2.5% for
two values of K
s
.
FIGURE 9.24
Values of M
so
for a beam clamped at
each end and carrying a mass at h
1
for which the error is less than 5%
and less than 2.5%.

0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
0
10
20
30
40
50
60
M
so
2.5%
5%
1
0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
20
40
60
80
100
120
140
M
so
2.5%
5%
1
FIGURE 9.25
Values of M
so
for a beam hinged at
each end and carrying a mass at h
1
for which the error is less than 5%
and less than 2.5%.
FIGURE 9.26
Values of M
so
for a cantilever beam
carrying a mass at h
1
for which
the error is less than 5% and less
than 2.5%.

the mass ratio should be greater than 3.5 and for a hinged-hinged beam the
mass ratio should be greater than 5. These mass ratio values must be increased
as the mass is located away from these respective locations, which are the lo-
cations where the beams have their minimum stiffness.
When the error is to be less than or equal to 2.5%, the mass ratios are on
the order of twice those needed to maintain 5%.
EXAMPLE 9.3
Determination of the properties of a beam supporting rotating machinery
An engineer has to mount to the center of a steel beam a piece of rotating ma-
chinery that weighs 50 kg and will spin at 1800 rpm. The beam is 3 m long,
weighs 100 kg, and is clamped at both ends. Refer to the system shown in Fig-
ure 9.27. In order to ensure that the beam is not excited at its fundamental nat-
ural frequency, the engineer would like the beam’s first natural frequency to
be three times that of the excitation frequency. We shall determine the mini-
mum radius gyration of the beam’s cross-section so that these requirements
are met. The beam’s Young’s modulus is N/m
2
, and its
density is r 7850 kg/m
3
; therefore,
m/s
The excitation frequency f
e
due to the rotating machinery is
(a)
Therefore, we need to determine the beam geometry so that the first natural
frequency
(b)
From Eq. (9.94) and Eq. (b), we have that
(c)
which, upon using Eq. (a), leads to
(d)
From the given parameters, we find that g
o
M
o
/m
o
50/100 0.5
and, therefore, from Table 9.7 that
1
1.2246p. Since L 3 m and c
b
5000 m/s, we obtain from Eq. (d) that
(e) 6.88
cm
r
180 p 3
2
5000 11.2246p 2
2
0.0688
m
r
6pL
2
f
e
c
b
2
1
180pL
2
c
b
2
1
f
1
c
b
r
2
1
2pL
2
3f
e
f
1
3f
e
90 Hz
f
e
1800 rev/min
60 s/min
30 Hz
c
b
2E/r 5,000
E 1.9625 10
11
612 CHAPTER 9 Vibrations of Beams
3 m
FIGURE 9.27
Beam clamped at each boundary
and excited by a rotating machine
mounted at its midpoint.

If the cross-section of the beam were rectangular, with width b and depth h,
then
(f)
and the depth of the beam is determined from Eqs. (e) and (f) to be
(g)
Notice that for a beam of rectangular cross-section, the width of the beam b
does not affect the natural frequency. However, it does affect the static dis-
placement of the beam. The equivalent stiffness of a beam clamped at each
boundary is provided in Case 6 of Table 2.3. From this expression, it is seen
that the displacement is proportional to I, which depends of the width b.
9.3.5
Beams with an Interior Mass, Spring, and Single
Degree-of-Freedom System Attached Simultaneously
30
We shall extend the results of Section 9.3.4 by considering a beam of length L
that has simultaneously attached at in-span locations a mass M
o
at x L
1
,a
spring of stiffness k
2
at x L
2
, and a single degree-of-freedom system with
mass M
s
and stiffness k
s
at x L
3
. Upon using Eqs. (9.107), (9.109), (9.111a),
(9.111b) and (9.115), we arrive at the following equation for the beam
(9.164)
and the following equation for the single degree-of-freedom system
(9.165)
If we assume that the beam and the attached single degree-of-freedom
system are undergoing harmonic oscillations of the form given by Eq. (9.112)
and we introduce the definitions of Eqs. (9.67) and (9.115), then Eqs. (9.164)
and (9.165) become, respectively,
(9.166)
K
s
3W1h2 Z
o
4d1h h
3
2 0
d
4
W1h 2
dh
4
4
31 g
o
d1h h
1
24W1h2 K
2
d1h h
2
2W1h2
M
s
d
2
z1t 2
dt
2
k
s
z1t 2 k
s
w1L
3
,t2
k
s
L
3w1x,t2 z1t 24d1x L
3
2 0
EI
0
4
w1x,t 2
0x
4
crA
M
o
m
o
d1x L
1
2d
0
2
w1x,t 2
0t
2
k
2
L
d1x L
2
2w1x,t2
h 2r23
2 6.88 23 23.83 cm
r
2
I
A
bh
3
12bh
h
2
12
9.3 Free Oscillations 613
30
A similar system has been analyzed using the Timoshenko beam theory; see, E. B. Magrab,
“Natural Frequencies and Mode Shapes of Timoshenko Beams with Attachments,” Journal of
Vibration and Control, 13, (7), 905–934 (2007).

and
(9.167)
where
s
is given by Eq. (9.116) and
Substituting Eq. (9.167) into Eq. (9.166), we obtain
(9.168)
where
(9.169)
and we have used Eq. (9.118).
It should be realized from Eqs. (9.168) and (9.169) that it is not neces-
sary to consider that we have three different types of attachments applied at
three locations. If, for example, we want to consider three single degree-
of-freedom systems attached at three different locations, then we can simply
change the definition of each F
j
accordingly. Conversely, we can have the
spring, mass, and single degree-of-freedom system all attached at the same
location; that is, h
1
h
2
h
3
. Another way to look at Eqs. (9.168) and
(9.169) is that the definitions of F
j
can be arbitrarily switched and if desired,
they can be made equivalent to each other. Consequently, Eq. (9.168) is a very
general formulation.
Boundary Conditions and Characteristic Equation
We assume that at h 0 the beam is restrained by a torsion spring of stiffness
k
tL
and a translation spring of stiffness k
L
. Then, the boundary conditions at
h 0 are
(9.170)
where
K
L
k
L
L
3
EI
,
K
tL
k
tL
L
EI
W‡10 2K
L
W10 2
W–10 2 K
tL
W¿10 2
F
3
B1 2
M
so
4
1
4
/
4
s
F
2
K
2
F
1
g
o
4
d
4
W1h 2
dh
4
4
W1h 2
a
3
j1
F
j
d1h h
j
2W1h2 0
h
j
L
j
L
j 1,2,3,
g
o
M
o
m
o
,
and
K
2
k
2
L
3
EI
a1
4
4
s
bZ
o
W1h
3
2
614 CHAPTER 9 Vibrations of Beams

At the end h 1, we assume that the beam is restrained by a torsion spring
of stiffness k
tR
and a translation spring of stiffness k
R
. In addition, a mass M
R
is attached. Then, the boundary conditions at h 1 are
(9.171)
where
and
(9.172)
Upon taking the Laplace transform of Eq. (9.168) and collecting terms,
we arrive at
(9.173)
where is the Laplace transform of W(h). Following the procedure used
to arrive at Eq. (9.125), we obtain for the inverse Laplace transform of
Eq. (9.173) that
(9.174)
where Q(j), R(j), S(j), and T(j) are defined in Eq. (9.80) and u(j) is the unit
step function.
To satisfy the boundary conditions, we first substitute Eq. (9.170) into
Eq. (9.174) to obtain
(9.175)
To determine W(0) and W(0), we substitute Eq. (9.175) into the bound-
ary conditions given by Eqs. (9.171) and use Eqs. (9.84) to arrive at
(9.176)A
21
1 2W102 A
22
1 2W¿10 2
1
2
a
3
j1
F
j
E
2j
1 2W1h
j
2
A
11
1 2W102 A
12
1 2W¿10 2
1
2
a
3
j1
F
j
E
1j
1 2W1h
j
2
1
3
a
3
j 1
F
j
W1h
j
2T13h h
j
42u1h h
j
2
W1h 2 3Q1h2 K
L
T1h 2/
3
4W102 3R1h2/K
tL
S1h 2/
2
4W¿10 2
W‡102T1h 2/
3
1
3
a
3
j 1
F
j
W1h
j
2T 13h h
j
42u1h h
j
2
W1h 2 W10 2Q1h2 W¿10 2R1h2/W–102S1h 2/
2
W
ˆ
1s 2
W
ˆ
1s 2
1
s
4
4
cW102s
3
W¿102s
2
W–102s W‡10 2
a
3
j1
F
j
e
sh
j
W1h
j
2d
g
R
M
R
m
o
K
R
k
R
L
3
EI
,
K
tR
k
tR
L
EI
W‡11 2 1K
R
g
R
4
2W112
W–11 2K
tR
W¿11 2
9.3 Free Oscillations 615

where
(9.177)
and
(9.178)
From Eq. (9.176), we obtain the following expressions for W(0) and W(0)
(9.179)
where
(9.180)
If F
1
F
2
0, then Eq. (9.179) reduces to Eq. (9.130) when M
R
0.
Upon substituting Eq. (9.179) into Eq. (9.175), we obtain
(9.181)
where
(9.182)
Equation (9.181) must be valid at each h
j
. Therefore, upon setting h h
j
,
j 1, 2, 3, in Eq. (9.181), we obtain the following system of equations
(9.183)
where is a (3 3) matrix whose elements are
(9.184)c
ij
1 2 F
j
3H
j
1h
i
, 2 T 1 3h
i
h
j
42u1h
i
h
j
24
3
d
ij
i,j 1,2,3
3C 4
3C 45W6 0
3R1h2 b
1
S1h 24h
2,j
1 2/D
o
1 2
H
j
1h, 23Q1h2 a
1
T 1h24h
1,j
1 2/D
o
1 2
W1h 2
1
3
a
3
j1
F
j
W 1h
j
23H
j
1h, 2 T 13h h
j
42u1h h
j
24
D
o
1 2 A
11
1 2A
22
1 2 A
12
1 2A
21
1 2
h
2,j
1 2 A
11
1 2E
2j
1 2 A
21
1 2E
1j
1 2
h
1,j
1 2 A
22
1 2E
1j
1 2 A
12
1 2E
2j
1 2
W¿10 2
1
2
D
o
1 2
a
3
j1
F
j
h
2,j
1 2W1h
j
2
W10 2
1
3
D
o
1 2
a
3
j1
F
j
h
1,j
1 2W1h
j
2
b
1
K
tL
,
b
2
K
tR
a
1
K
L
3
,
a
2
1
3
1K
R
g
R
4
2
E
2j
1 2 a
2
T 131 h
j
42 Q1 31 h
j
42
E
1j
1 2 R131 h
j
42 b
2
S131 h
j
42
A
22
1 2 11 a
2
b
1
2S12 b
1
T 12 a
2
R12
A
21
1 2 R12 1a
2
a
1
2Q 12 a
2
a
1
T12
A
12
1 2 1b
2
b
1
2Q12 T 1 2 b
2
b
1
R12
A
11
1 2 11 a
1
b
2
2S12 b
2
T 12 a
1
S12
616 CHAPTER 9 Vibrations of Beams

!
ij
is the Kronecker delta, and {W}isa(31) vector with elements W(h
i
), i
1, 2, 3. The natural-frequency coefficients
n
are those values of that satisfy
(9.185)
The corresponding mode shape is
(9.186)
where
(9.187)
c
ij,n
c
ij
(
n
), and we have introduced the normalization
The modal displacement of the single degree-of-freedom system is
(9.188)
When there are only two in-span attachments on the beam, say F
3
0,
then the mode shape is given by
(9.189)
where
(9.190)
Equations (9.185) and (9.186) are for the boundary conditions given by
Eqs. (9.170) and (9.171). They can be reduced to the various combinations of
boundary conditions shown in Table 9.1 by using the procedure discussed in
Section 9.3.3. It is noticed that the results presented by Eqs. (9.170) and
(9.171) have, in effect, been uncoupled from the specific form of the bound-
ary conditions. This is a direct consequence of the Laplace transform solution
method, which reduced a system with four unknown constants to a system
with two unknown constants, thereby making it algebraically practical to ob-
tain the solution given above.
M
2n
c
11,n
c
12,n
M
1n
1
W
n
1h 2
a
2
j 1
F
jn
M
jn
3H
j
1h,
n
2 T 1 3h h
j
42u1h h
j
24
Z
o,n
W
n
1h
3
2a1
4
n
4
s
b
1
W
n
1h 2
3
n
W
n
1h
1
2
W1h 2
F
1n
g
o
4
n
,
F
2n
K
2
,
F
3n
B1
n
2
M
3n
c
11,n
c
22,n
c
12,n
c
21,n
c
12,n
c
23,n
c
22,n
c
13,n
M
2n
c
13,n
c
21,n
c
11,n
c
23,n
c
12,n
c
23,n
c
22,n
c
13,n
M
1n
1
W
n
1h 2
a
3
j1
F
jn
M
jn
3H
j
1h,
n
2 T 1 3h h
j
42u1h h
j
24
det 0C 0 0
9.3 Free Oscillations 617
Beam with mass, spring, and vibration absorber attached at the same
location We shall consider a beam with a mass M
o
, a spring k
2
, and a single
degree-of-freedom system with mass M
s
and stiffness k
s
that are all attached
at the same location; that is, h
1
h
2
h
3
. Then, from Eqs. (9.177), (9.180)
and (9.182), we find that
(9.191)
where
(9.192)
Therefore, from Eq. (9.182), we see that
(9.193)
where
(9.194)
It is noted that H
1
(h,) is identical to Eq. (9.133) and that E
i
and h
i
, i 1, 2,
are the same as those given in Eqs. (9.129a). Using Eqs. (9.191) and (9.192)
in Eq. (9.184), we obtain
(9.195)
and we have used the fact that T(0) 0. Upon substituting Eq. (9.195) into
Eq. (9.185), we arrive at
(9.196)
The corresponding mode shape becomes
(9.197)
where, for convenience, we have set the scale factor
a
3
j 1
F
jn
M
jn
1
W
n
1h 2 H
1
1h,
n
2 T 1
n
3h h
1
42u1h h
1
2
3
n
H1h
1
,
n
21g
o
4
n
K
2
B1
n
22 0
c
ij,n
F
j
H
1
1h
1
,
n
2
3
n
d
ij
i, j 1,2,3
3R1h2 b
1
S1h 24h
2
1 2/D
o
1 2
H
1
1h, 23Q1h2 a
1
T 1h24h
1
1 2/D
o
1 2
H
1
1h, 2 H
2
1h, 2 H
3
1h, 2
h
2
1 2 A
11
1 2E
2
1 2 A
21
1 2E
1
1 2
h
1
1 2 A
22
1 2E
1
1 2 A
12
1 2E
2
1 2
E
2
1 2 a
2
T131 h
1
42 Q1 31 h
1
42
E
1
1 2 R131 h
1
42 b
2
S131 h
1
42
h
2,j
1 2 h
2
1 2
h
1,j
1 2 h
1
1 2
E
2j
1 2 E
2
1 2
j 1,2,3
E
1j
1 2 E
1
1 2
618 CHAPTER 9 Vibrations of Beams
It is noted that Eq. (9.196) is the same as Eq. (9.134) if, in Eq. (9.134),
we replace B(
n
) with
(9.198)
and that Eq. (9.197) is the same as Eq. (9.136). Therefore, if we employ
Eq. (9.198) in Eqs. (9.134) and (9.136), then we can use the relations given by
Eqs. (9.143) through (9.155). The modal displacement of the single degree-
of-freedom system is given by Eq. (9.137).
It was found in Section 8.6.1 that if one selected the natural frequency of
the absorber to equal the natural frequency of the system without the absorber,
then the frequency-response function was equal to zero at this frequency.
Hence, we shall use the same reasoning and select
s
M,1
, where
M,1
is
the lowest natural-frequency coefficient for a beam that is only carrying the
mass M
o
at a location h
1
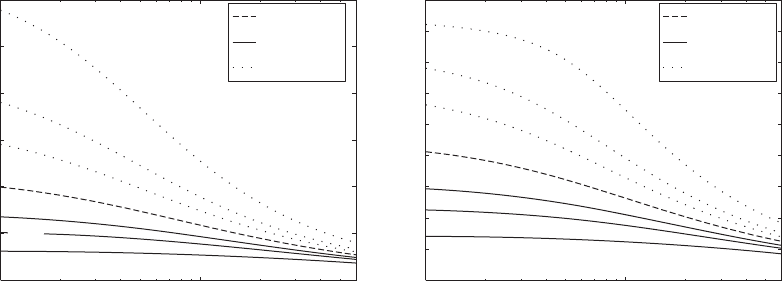
. Using this assumption, we have plotted the lowest
two natural-frequency coefficients in Figure 9.28 to Figure 9.30 as a
function g
o
for M
so
equal to 0.3, 1, and 4 and for h
1
0.5 and h
1
0.35 for
a beam clamped at both ends, a beam hinged at both ends, and a cantilever
beam, respectively. For reference, we have also plotted as a function of
g
o
. In these figures, we have chosen to plot rather than
1,2
because
is proportional to the radian natural frequency v
1,2
; recall Eq. (9.67).
We now compare the results just obtained with those obtained from ap-
proximating this system as a two-degree-of-freedom system. This two-
degree-of-freedom system is composed of the single degree-of-freedom
system formed by the beam with stiffness k
beam
and the mass M
o
. The other
single degree-of-freedom system is composed of the mass M
s
and spring with
2
1,2
2
1,2
2
M,1
2
1,2
B1
n
2씮 g
o
4
n
K
2
B1
n
2
9.3 Free Oscillations 619
10
1
10
0
0
10
20
30
40
50
60
o
Ω
2
M
so
4
M
so
1
M
so
0.3
M
so
0.3
M
so
1
M
so
4
10
0.78
Ω
s
2
Ω
2
M,1
Ω
1
2
Ω
2
2
Ω
s
2
Ω
2
M,1
Ω
1
2
Ω
2
2
Ω
2
M
so
4
M
so
1
M
so
0.3
M
so
0.3
M
so
1
M
so
4
10
1
10
0
o
10
0.78
0
(a) (b)
5
10
15
20
25
30
35
40
45
FIGURE 9.28
Lowest two natural-frequency coefficients for a clamped-clamped beam carrying a mass and a single degree-of-freedom system at the
same location: (a) h
1
0.5 and (b) h
1
0.35.
