Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


While displacement-mode shapes are important for determining loca-
tions of displacement sensors, velocity sensors, and accelerometer sensors,
strain-mode shapes are important for determining the locations of strain sen-
sors. For design purposes, the information about locations of sensors and
actuators with reference to nodes of a mode is put forth in the form of the fol-
lowing guidelines.
Natural frequency comparisons for different boundary conditions We
now examine the percentage differences in the lowest natural frequency in
beams with different boundary conditions, namely, clamped at both ends,
hinged at both ends, clamped at one end and hinged at the other, and clamped
at one end and free at the other. We assume that the beam material and geom-
etry are the same in each case and that only the boundary conditions are dif-
ferent from one case to another. The natural frequencies of the beam clamped
at both ends are used as reference values for the calculations. Then, from
Table 9.3, we determine the following
where
ch
is the measure of how much the first natural frequency f
1,ch
of a
clamped-hinged beam is below the first natural frequency f
1,cc
of the
clamped-clamped beam,
hh
is the measure of how much the first natural fre-
quency f
1,hh
of a hinged-hinged beam is below the first natural frequency
f
1,cc
of the clamped-clamped beam, and
cf
is the measure of how much the
first natural frequency f
1,cf
of a cantilever beam is below the first natural fre-
quency f
1,cc
of the clamped-clamped beam. Thus, the clamped-pinned
beam’s natural frequency is 31% lower than that of a beam clamped at each
end and the cantilever beam’s natural frequency is 84% lower than that of a
beam clamped at each end. These observations lend themselves to the fol-
lowing design guideline.
¢
cf
100 a
1,cf
2
1,cc
2
1b 100 a
10.5969p 2
2
11.5056p 2
2
1b84.3%
¢
hh
100 a
1,hh
2
1,cc
2
1b 100 a
1p2
2
11.5056p2
2
1b55.9%
¢
ch
100 a
f
1n,ch
f
1n,cc
1b 100 a
2
1,ch
2
1,cc
1b 100 a
11.25p2
2
11.5056p2
2
1b31.1%
580 CHAPTER 9 Vibrations of Beams
Design Guidelines: For a system modeled as a beam, if a sensor
needs to be located so as to sense the vibrations in a certain mode, then
this sensor should be located away from the nodes of this mode. Simi-
larly, in order to actuate or excite a certain vibration mode, the actuator
should be away from the node of this mode. Alternatively, if a sensor
should not sense a certain vibration mode or an actuator should not
excite a certain vibration mode, then they should be located at a node
of that mode.

We note from Table 9.3 that as the frequency mode number n becomes
large, the natural frequency coefficients for different boundary conditions
tend towards the same value: np. Thus, for natural frequencies higher than the
tenth (n 10), the beam can be approximated as if it were hinged at both its
ends; in this region the error in the natural frequencies will be less then 5%.
Beam free at both ends We now consider a beam that is free at both ends,
which is given by Case 5 of Tables 9.2 and 9.3. It is seen in Table 9.3 that the
natural frequency coefficients are the same as those for a beam clamped at
both ends. However, the mode shapes are different. The mode shape corre-
sponding to the nth nondimensional frequency coefficient
n
has (n 1)
node points; that is, there are two node points in the first mode, and so forth.
Correspondingly, for the beam clamped at both ends, there are (n 1) node
points in the interior of the beam. Examples of practical applications that use
models of beams free at both ends are the study of the vibrations of launch ve-
hicles
23
and ships.
In addition to the mode shapes shown in Table 9.3, a beam free at both
ends also has rigid-body modes whose form is given by
(9.102)
Both modes given in Eq. (9.102) are associated with
n
0; that is, the nat-
ural frequency in each case is zero; thus, the zero eigenvalue corresponds to a
nontrivial mode shape in this case. The first of the expressions in Eqs. (9.102)
represents a case where every point on the beam experiences the same trans-
lation, and the second of these expressions represents a case where every
point on the beam experiences a combination of translation and rotation. Un-
like the flexural modes of vibration given in Case 5 of Table 9.2, for the rigid-
body modes given by Eq. (9.102), d
2
W
n
/dh
2
is zero everywhere on the beam
and hence, the strain associated with vibrations in a rigid-body mode is zero
everywhere on the beam.
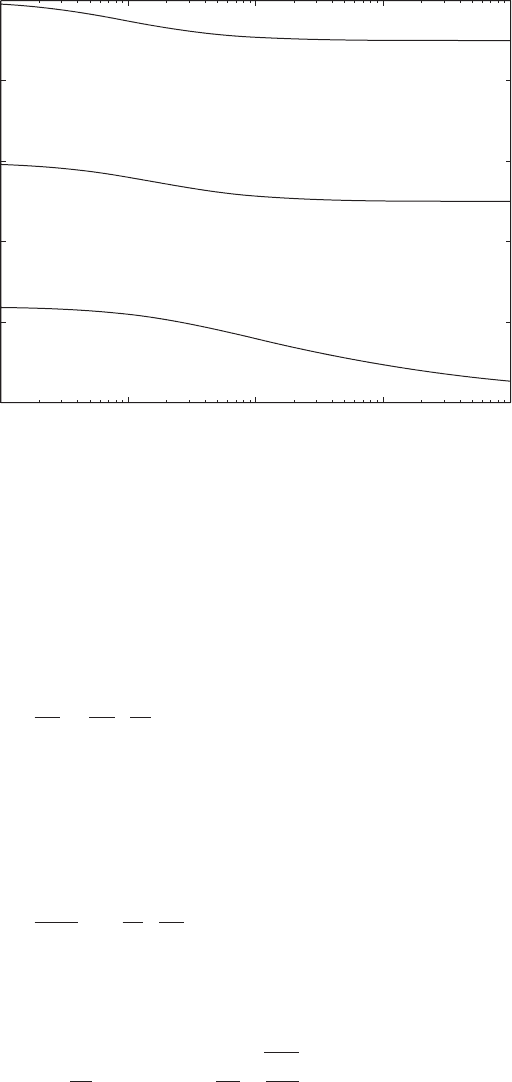
Cantilever beam with a mass at the free end The natural-frequency coeffi-
cients and corresponding mode shapes for a cantilever beam with a mass at
the free end are given Table 9.4 and the variations of the lowest three natural
frequency-coefficients as a function M
o
/m
o
are given in Figure 9.8. From
Eq. (6a) of Table 9.2, we see that when the ratio of the attached mass to the
mass of the beam M
o
/m
o
becomes very large, the characteristic equation and
mode shapes approach the characteristic equation and mode shapes of a beam
W
n
1h 2 C
0
and
W
n
1h 2 D
0
E
0
h
9.3 Free Oscillations 581
23
A. Joshi, “Prediction of Free-Free Modes from Single Point Support Ground Vibration Test of
Launch Vehicles,” J. Sound Vibration, Vol. 216, No. 4, pp. 739–747 (1998).
Design Guideline: For uniform beams having the same material and
same geometry, the beam clamped at both ends has the highest funda-
mental natural frequency.
clamped at one end and hinged at the other, which are given by Eqs. (3a) and
(3b) of Table 9.2. When M
o
/m
o
becomes very small, the characteristic equa-
tion and mode shapes approach the characteristic equation and mode shapes
of a beam clamped at one end and free at the other, which are given by
Eqs. (4a) and (4b), respectively, of Table 9.2. The nondimensional natural-
frequency coefficient
1
approaches zero as M
o
/m
o
approaches infinity. Thus,
in the limit, the nth mode of a cantilever beam with a mass at the free end be-
comes the (n 1)th mode of a beam clamped at one end and hinged at the
other. An example of a system that is modeled as a cantilever beam with a
mass on its free end is a water tower.
In many instances where a beam carries an end mass, the inertia of
the beam is neglected and the system is represented by an equivalent single
582 CHAPTER 9 Vibrations of Beams
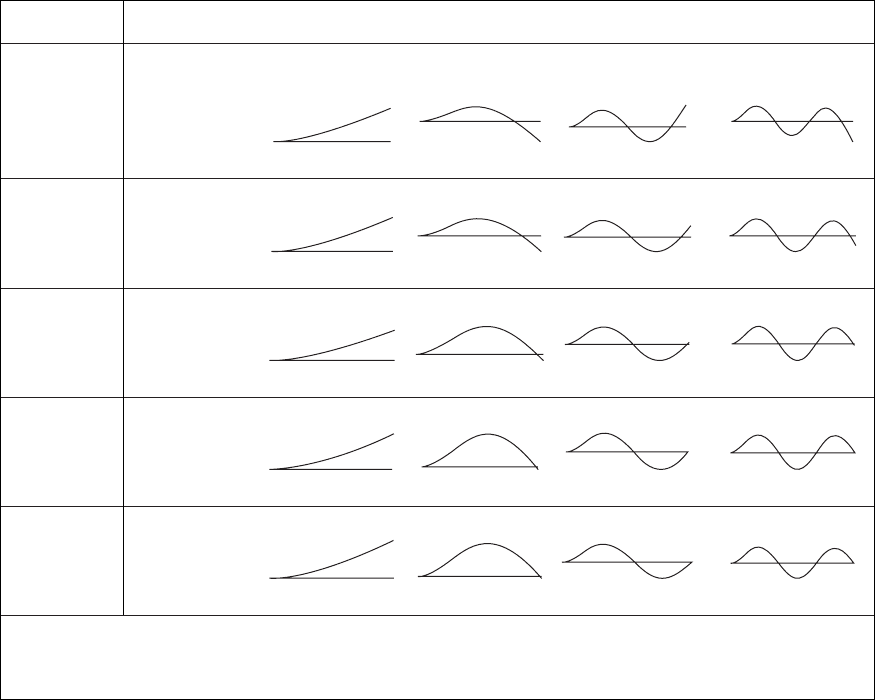
TABLE 9.4
Natural-Frequency Coefficients, Mode Shapes and Interior Node Points for a Cantilever Beam with Mass at Free End:
Case 6 of Table 9.2.
M
o
/m
o
n 1 n 2 n 3 n 4
n
/p
‡
0.5969 1.4942 2.5002 3.5000
(n 0.5, n 4)
0.0 Mode shapes
Node points
*
None 0.783 0.504, 0.868 0.358, 0.644, 0.906
n
/p
‡
0.5484 1.4004 2.3717 3.3492
Mode shapes0.1
Node points
*
None 0.841 0.530, 0.921 0.375, 0.673, 0.953
n
/p
‡
0.3972 1.2832 2.2709 3.2648
Mode shapes1.0
Node points
*
None 0.953 0.55, 0.983 0.384, 0.689, 0.991
n
/p
‡
0.2769 1.2573
†
2.2544
†
3.2531
†
Mode shapes5.0
Node points
*
None 0.988 0.55, 0.996 0.386, 0.692, 0.998
n
/p
‡
0.2342 1.2537
†
2.2522
†
3.2516
†
Mode shapes10.0
Node points
*
None 0.994 0.557, 0.998 0.386, 0.692, 0.999
‡
The natural frequency f
n
in Hertz as a function of
n
is given by Eq. (9.94).
*
Values of h not including the boundaries.
†
Approaches (n 1)th natural frequency and mode shape for the clamped-hinged boundary conditions.
9.3 Free Oscillations 583
degree-of-freedom system. This situation is revisited to point out when it is
reasonable to neglect the beam inertia and when it is not. For a beam with an
end mass, the natural frequency of the equivalent single degree-of-freedom
system is determined by making use of the stiffness expressions listed in
Table 2.3. For a cantilever beam with an end mass, we make use of Case 4 of
Table 2.3 and find that the natural frequency is
(9.103)
Equation (9.103) is the result obtained by approximating the first natural fre-
quency of a cantilever beam with an end mass as the natural frequency of a
single degree-of-freedom system where only the beam stiffness is taken into
account and the beam inertia is neglected. However, when the beam inertia is
not neglected, the first natural frequency v
1
is obtained from Eq. (9.67) as
(9.104)
where
1
is the lowest natural-frequency coefficient obtained by solving
Eq. (6a) in Table 9.2. On comparing Eqs. (9.103) and (9.104), the percentage
error one incurs in using Eq. (9.103) is
(9.105)e 100 a
v
n
v
1
1b 100 a
1
2
1
B
3m
o
M
o
1b %
v
2
1
EI
4
1
rAL
4
a
EI
L
3
b
4
1
m
o
v
2
n
k
M
o
3
M
o
a
EI
L
3
b
10
2
10
1
10
0
10
1
10
2
0
0.5
1
1.5
2
2.5
Ω
1
/
Ω
2
/
Ω
3
/
Ω
n
/
M
o
/m
o
FIGURE 9.8
First three natural-frequency coeffi-
cients for a cantilever beam carrying
a mass at its free end as a function
of M
o
/m
o
.

Determining
1
from Eq. (6a) in Table 9.2 for a given M
o
/m
o
, we find from
Eq. (9.104) that we have an error e 5% when the mass ratio M
o
/m
o
2.3
and that we have an error e 1% when the mass ratio M
o
/m
o
11.7. For
M
o
/m
o
1, the error is 11.2%. This leads to the following design guideline.
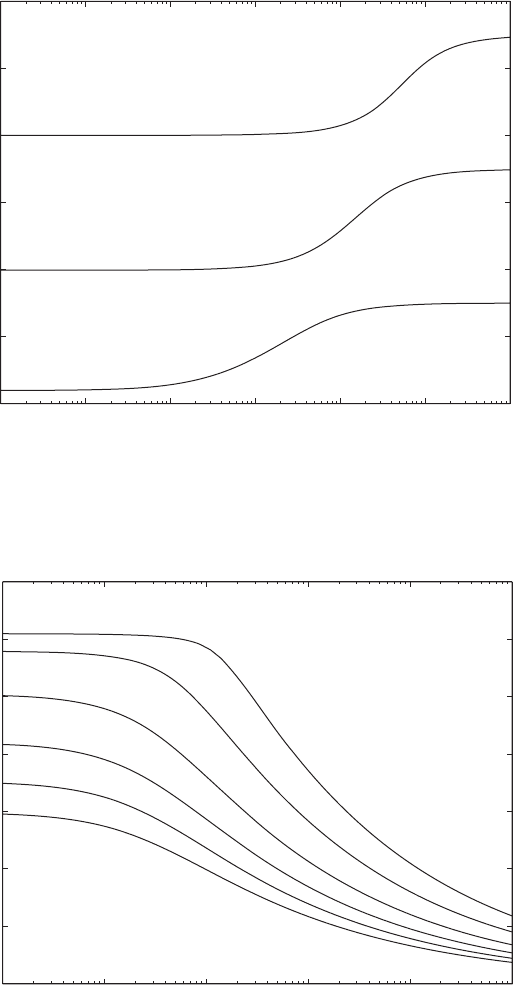
Cantilever beam restrained by a translation spring at the free end The
natural-frequency coefficients and corresponding mode shapes for a cantilever
beam with a translation spring of nondimensional stiffness K
2
at its free end are
given Table 9.5 and the variations of the lowest three natural-frequency coeffi-
cients as a function K
2
are given in Figure 9.9. From Eqs. (7a) and (7b) in Table
9.2, we see that as K
2
becomes very large, the characteristic equation and mode
shapes approach the characteristic equation and mode shapes of a beam
clamped at one end and hinged at the other, which are given by Eqs. (3a) and
(3b), respectively, in Table 9.2. On the other hand, as K
2
becomes very small,
the characteristic equation and mode shapes approach those of a beam clamped
at one end and free at the other, which are given by Eqs. (4a) and (4b), respec-
tively, in Table 9.2. Comparing these limiting cases to the case of a cantilever
carrying a mass at its free end, we see that although the beams have very dif-
ferent physical constraints, they have identical limiting cases. However, there
is one very important difference: when the stiffness of the end spring increases,
the natural frequencies increase whereas for a cantilever beam with a mass, as
the magnitude of the mass increases the natural frequencies decrease. A can-
tilever beam with a translational spring at its free end has been used to model
the vibration characteristics of atomic-force microscope cantilevers.
24
Beam restrained by translation springs at both ends From Eqs. (8a) and
(8b) in Table 9.2, we see that when K
1
and K
2
become very large, the charac-
teristic equation and mode shapes approach the characteristic equation and
mode shapes of a beam pinned at each end, which are given by Eqs. (2a) and
(2b), respectively, in Table 9.2. At the other extreme, as both K
1
and K
2
be-
come very small in magnitude, the characteristic equation and mode shapes
approach the characteristic equation and mode shapes of a beam free at both
ends, which are given by Eqs. (5a) and (5b), respectively, in Table 9.2.
584 CHAPTER 9 Vibrations of Beams
24
U. Rabe, K. Janser, and W. Arnold, “Vibrations of Free and Surface-Coupled Atomic Force
Microscope Cantilevers: Theory and Experiment,” Review Scientific Instruments, Vol. 67, No. 9,
pp. 3281–3293 (1996).
Design Guideline: When a cantilever beam of mass m
o
and an end
mass M
o
is approximated by a single degree-of-freedom system where
the beam stiffness is taken into account and the beam inertia is neg-
lected, the approximation for the first natural frequency obtained by us-
ing the single degree-of-freedom model is reasonable to use only when
the ratio of the end mass to the beam mass M
o
/m
o
is greater than 2.3.
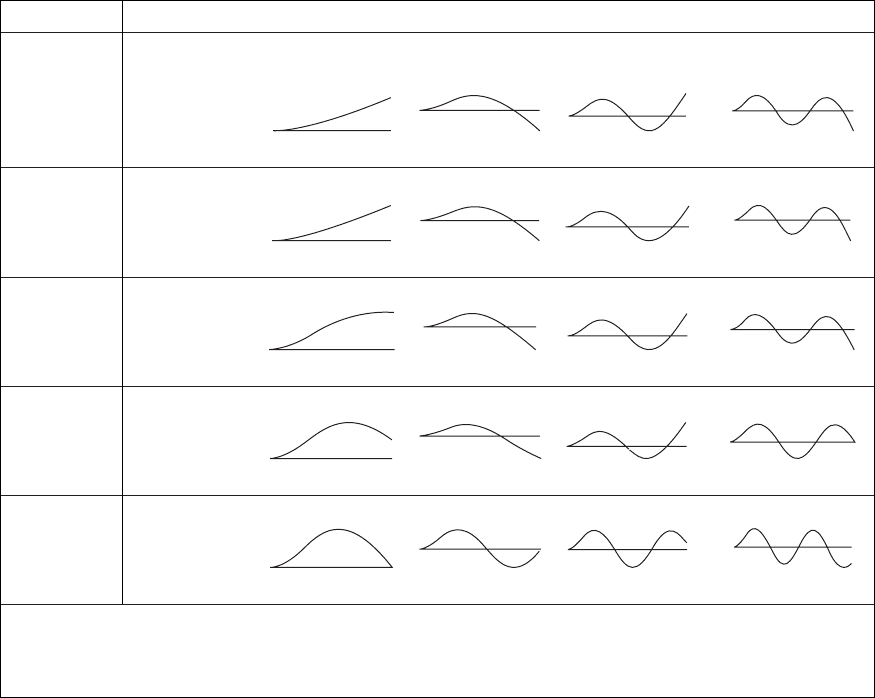
K
2
n 1 n 2 n 3 n 4
n
/p
‡
0.5969 1.4942 2.5002 3.5000
(n 0.5, n 4)
0 Mode shapes
Node points
*
None 0.783 0.504, 0.868 0.358, 0.644, 0.906
n
/p
‡
0.7046 1.5035 2.5022 3.5007
3
Mode shapes
Node points
*
None 0.779 0.503, 0.867 0.358, 0.644, 0.905
n
/p
‡
1.0083 1.5919 2.5207 3.5073
30 Mode shapes
Node points
*
None 0.739 0.499, 0.861 0.358, 0.643, 0.904
n
/p
‡
1.1588 1.7876 2.5732 3.5252
100 Mode shapes
Node points
*
None 0.673 0.489, 0.844 0.356, 0.639, 0.899
n
/p
*‡
1.2468
†
2.2306
†
3.1869 4.0906
3000 Mode shapes
Node points
*
None 0.562 0.394, 0.705 0.307, 0.550, 0.792
‡
The natural frequency f
n
in Hertz as a function of
n
is given by Eq. (9.94).
*
Values of h not including the boundaries.
†
Approaches natural frequency and mode shape for the clamped-hinged boundary conditions.
Beam restrained by torsion springs at both ends From Eqs. (9a) and (9b)
in Table 9.2, it is seen that as both B
1
and B
2
become very large, the charac-
teristic equation and mode shapes approach those of a beam clamped at each
end, as given by Eqs. (1a) and (1b), respectively, in Table 9.2. When both B
1
and B
2
become very small, the characteristic equation and mode shapes ap-
proach those of a beam pinned at both ends, as given by Eqs. (2a) and (2b),
respectively, in Table 9.2.
Cantilever beam with mass and translation spring at the free end To de-
termine the effects of both a mass and spring attached at the free end of a
cantilever beam, a plot of the first natural-frequency coefficient of Case 10 of
Table 9.2 is given in Figure 9.10. It is seen that as K
2
increases the first natu-
ral coefficient increases regardless of the magnitude of the mass ratio M
o
/m
o
.
9.3 Free Oscillations 585
TABLE 9.5
Natural-Frequency Coefficients, Mode Shapes and Interior Node Points for a Cantilever Beam with Spring at Free End:
Case 7 in Table 9.2.
10
1
10
0
10
1
10
2
10
3
10
4
0.5
1
1.5
2
2.5
3
3.5
K
2
10
2
Ω
3
/
Ω
2
/
Ω
1
/
Ω
n
/
FIGURE 9.9
First three natural-frequency coefficients for a cantilever beam with a translation spring at the
free end as a function of the spring stiffness K
2
.
FIGURE 9.10
Lowest natural-frequency coefficient for a cantilever beam with a mass and spring attached
to the free end as a function of M
o
/m
o
for several values of K
2
.
10
2
10
1
10
0
10
1
10
2
10
3
0
0.2
0.4
0.6
0.8
1
1.2
1.4
K
2
0
K
2
3
K
2
10
K
2
30
K
2
100
K
2
300
M
o
/m
o
Ω
1
/

EXAMPLE 9.2 Beams with attachments: maintaining a constant first natural frequency
Consider a cantilever beam whose lowest natural frequency is v
1
. A mass M
o
is placed on the free end of the beam, with the requirement that the lowest nat-
ural frequency of this new system be equal to v
1
. There are two ways in which
this can be done: (1) by changing the cross-sectional properties of the beam
and (2) by adding a translation spring to the mass. To employ the first method,
we use Eq. (9.94) and note that
(a)
where is a constant, r is the radius of gyration of the beam
without the mass, r
M
is the radius of gyration of the beam with the mass,
v
M1
is the natural frequency of the system with the mass,
1
is the natural-
frequency coefficient as determined from Eq. (4a) in Table 9.2, and
M1
is the
corresponding natural-frequency coefficient as determined from Eq. (6a) in
Table 9.2. Since the requirement is that v
1
v
M1
, and the material and length
of both beam configurations are the same, from Eq. (a) we find that
(b)
Thus, we must increase (since
M1
1
) the radius of gyration of the beam
with the mass by the ratio (
1
M1
)
2
. For example, if the ratio M
o
/m
o
1,
then from Table 9.4 we have that
M1
0.3972p and
1
0.5969p. There-
fore, (
1
M1
)
2
(0.5969/0.3972)
2
2.26 and r has to be increased by a fac-
tor of 2.26.
The second way to keep the natural frequency constant is to add a trans-
lation spring k
2
to the mass and adjust the stiffness k
2
so that natural frequency
remains the same. Since we are implicitly requiring that the beam properties
and geometry be constant for both systems, the task is to find for a given value
of M
o
the value of k
2
that ensures the first natural-frequency coefficient is con-
stant; that is,
(c)
where
KM1
is the natural-frequency coefficient of the system with the mass
and translation spring. The value of k
2
(as determined from its non dimen-
sional counterpart K
2
) is obtained by using Eq. (10a) in Table 2; that is,
(d)
where M
o
/m
o
is given and
1
0.5969p is the lowest root of
(e)cos1
1
2cosh1
1
2 1 0
a
K
2
1
3
1
M
0
m
0
b3cos1
1
2sinh1
1
2 sin1
1
2cosh1
1
24 cos1
1
2cosh1
1
2 1 0
1
KM1
r
M
r
1
2
M1
2
c
o
1E
/
r
/
L
2
v
M1
c
o
r
M
M1
2
v
1
c
o
r
1
2
9.3 Free Oscillations 587

588 CHAPTER 9 Vibrations of Beams
which is obtained from Eq. (4a) in Table 9.2. Consequently, Eq. (d) simpli-
fies to
(f)
Since the quantity inside the right-hand brackets does not equal zero, we see
that Eq. (f) is satisfied when
(g)
Thus, by choosing a value of K
2
as indicated in Eq. (g), the system with the
attached mass and translation spring will have the same first natural frequency
as the system without the mass and spring. For example, if we again select the
ratio M
o
/m
o
1, and since
1
0.5969p, Eq. (g) leads to K
2
(0.5969p)
4
12.37. From Table 2.3, we find that the stiffness of a cantilever beam with
a load at its free end is k
c
3EI/ L
3
. Therefore, from the definition of K
2
in
Eq. (9.67), we obtain that K
2
3k
2
/k
c
. Thus, k
2
K
2
k
c
/3 (12.37/3)k
c
4.12k
c
. In other words, the stiffness of the spring attached at the free end has
to have a stiffness that is about four times that of the stiffness of the beam it-
self when loaded at its free end.
9.3.4 Effects of Stiffness and Inertial Elements Attached
at an Interior Location
25
In the previous sections, we considered free vibrations of beams that had
springs and inertia elements attached at the boundaries. In this section, we
shall extend these results and examine the free vibrations of beams that have
springs and inertia elements attached to an interior point of the beam. In par-
ticular, we shall determine the natural frequency coefficients and modes
shapes for the three configurations shown in Figure 9.11: (1) a beam with an
attached translation spring, (2) a beam with an attached mass, and (3) a beam
with an attached undamped single degree-of-freedom system. In all three
cases, it is assumed that the beam has a uniform cross-section. We shall first
give the governing equation for each of these systems and then determine the
complete solution only for the case of a beam with an attached single degree-
of-freedom system. It will be shown that special cases of this system are the
beam with an attached mass and the beam with an attached spring. The case
of a beam with a single degree-of-freedom system attached at an interior point
is in effect a beam with a vibration absorber,
26
which was discussed in the
context of two degree-of-freedom systems in Section 8.6.
K
2
1
4
M
0
m
0
a
K
2
1
3
1
M
0
m
0
b3cos1
1
2sinh1
1
2 sin1
1
2cosh1
1
24 0
25
This type of analysis has been extended to include two degree-of-freedom systems. See, for
example, M. U. Jen and E. B. Magrab, “Natural Frequencies and Modes Shapes of Beams
Carrying a Two Degree-of-Freedom Spring-Mass System,” J. Vibrations Acoustics, Vol. 115,
pp. 202–209 (April 1993) and H. Ashrafiuon, “Optimal Design of Vibration Absorber Systems
Supported by Elastic Base,” J. Vibrations Acoustics, Vol. 114, pp. 280–283 (April 1992).
26
For the attachment of absorbers to more complex systems, see E. O. Ayorinde and G. B. War-
burton, op cit., 1980.
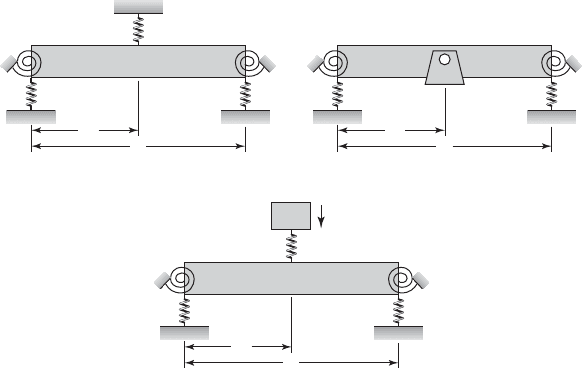
9.3 Free Oscillations 589
For each of the beams shown in Figure 9.11, at the left boundary x 0,
there is a linear translation spring with stiffness k
1
and a linear torsion spring
with stiffness k
t1
. At the right boundary x L, there are a linear translation
spring with stiffness k
2
and a linear torsion spring with stiffness k
t2
. In addi-
tion, as shown Figure 9.11a, a linear translation spring with stiffness k
s
is
attached at x L
1
,0 L
1
L. In Figure 9.11b, a mass M
s
is attached at
x L
1
,0 L
1
L. Finally, in Figure 9.11c, an undamped single degree-of-
freedom system of mass M
s
and stiffness k
s
is attached to the beam
27
at x L
1
,
0 L
1
L.
The discussion is limited to cases where the axial load p(x,t) 0 and the
externally applied transverse load f (x,t) 0. Furthermore, the oscillations are
assumed to be about the equilibrium position in each case. A primary feature
of the equations in each case is the representation of the discrete element as
an equivalent distributed element by using the delta function d(x).
Linear Spring Attached to an Interior Point x L
1
The governing equation of motion for the system shown in Figure 9.11a
is obtained from Eq. (9.40) by representing the discrete spring k
s
as a
k
2
k
1
k
s
k
t1
k
t2
L
1
L
(a)
k
2
k
1
k
t1
k
t2
L
1
L
(b)
M
s
k
2
k
1
k
s
k
t1
k
t2
L
1
L
(c)
z(t)
M
s
27
It is mentioned that these limits on L
1
can be removed in certain cases. Consider a cantilever
beam with a mass attached to its free end. One could formulate this situation by considering the
beam to be uniform and to include the mass as part of the boundary condition. On the other hand,
one could assume that the moment and shear are zero at the free end of the beam and that the at-
tached mass on the interior of the beam is moved to L
1
L.
FIGURE 9.11
Uniform and homogeneous beam with discrete elements at the boundaries and the following:
(a) a spring attached at x L
1
; (b) a mass attached at x L
1
; and (c) an undamped single
degree-of-freedom system attached at x L
1
.
