Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

indicates the slope at the boundary x  L, and so on. Also,

the translational velocity of the center of mass of the rigid body is denoted as

, the angular rotation of the torsion spring is denoted as , and the angu-

lar velocity of the rigid body is denoted as .

Recalling that the Lagrangian L

is the difference between the system ki-

netic energy and system potential energy, for the beam system it is given by

(9.22a)

where G

is given by Eq. (9.19), G

is given by Eq. (9.20), and G

is given

by Eq. (9.21). These last two terms on the right-hand side of Eq. (9.22a)

are included in the spatial integral by using the delta function introduced in

Chapter 6. This leads to

(9.22b)

where

(9.23)

In Eqs. (9.22b) and (9.23), the delta function is used to represent contributions

from the discrete attachments at the spatial locations x  0 and x  L. Specif-

ically, d(x) assumes a zero value when x is different from zero, and d(x  L)

assumes a zero value when x is different from L. The use of these functions

enables us to include the discrete contributions in an expression involving the

whole domain.

The damper elements at the boundaries introduce the following discrete

nonconservative forces at the boundaries:

(9.24)

9.2.3 Extended Hamilton’s Principle and Derivation of

Equations of Motion

To derive the governing equations of motion of the beam, we employ the ex-

tended Hamilton’s principle.A general formulation applicable to spatially one-

dimensional continua is ﬁrst presented, and the beam equation is obtained

as one application of this formulation. First, conservative systems—that is,

nc0

1t 2c

and

ncL

1t 2c

G1x,t,w,w

,w¿,w

¿,w– 2 G

 G

d1x 2 G

d1x  L 2





G1x,t,w,w

,w¿,w

¿,w– 2dx





1x,t,w,w

,w¿,w

¿,w– 2 G

d1x 2 G

d1x  L 24dx





1x,t,w,w

,w¿,w

¿,w– 2dx  G

 G

w¿

 0w1L,t2/0x

550 CHAPTER 9 Vibrations of Beams

Since the system is conservative, the work done by conservative forces in Eq. (9.16) is replaced

by the equivalent potential energy.

9.2 Governing Equations of Motion 551

systems without losses due to damping and other dissipation sources—are con-

sidered and then nonconservative systems are considered.

Conservative Systems

The statement of the extended Hamilton’s principle

for holonomic and con-

servative systems is as follows. Of all possible paths of motion to be taken be-

tween two instants of time t

and t

, the actual path to be taken by the system

corresponds to a stationary value of the integral I

; that is,

(9.25)

where d is the variation operator

and

(9.26)

In arriving at Eq. (9.26), we have made use of Eqs. (9.22) for the Lagrangian

of the system.

The ﬁrst term inside the integral on the right-hand side of Eq. (9.26) rep-

resents the contributions to the system kinetic energy, the system potential en-

ergy, and the work done in the continuum (beam) interior 0  x  L.The





1x,t,w,w

,w¿,w

¿,w– 2dx  G

 G

Tdt





 0

The extended Hamilton’s principle is expressed as

where d is the variation operator, the times t

and t

are the initial time and the ﬁnal time, respectively,

T is the total system kinetic energy, and dW includes work done by both conservative and nonconser-

vative forces. In the absence of nonconservative forces, dW dV, where V is the total system po-

tential energy. Hence, for conservative systems, the extended Hamilton’s principle is written as

or, equivalently as

where L

 T  V is the Lagrangian of the system.

The symbol d is used everywhere else in the book to mean the delta function; this is the only

exception.



dt  0



1dT  dV 2dt  0



1dT  dW 2dt  0

second and third terms on the right-hand side of Eq. (9.26) represent contribu-

tions from the discrete elements attached at the boundaries x  0 and x  L,

respectively. The damper elements at the boundaries, which are shown in Fig-

ure 9.4, are not considered in the conservative case.

By using calculus of variations, it can be shown

that Eq. (9.26) has a

stationary value when the following conditions are satisﬁed in the interior

0  x  L and at the boundaries x  0 and x  L.

Continuum interior (0  x  L)

(9.27)

Boundary conditions at x  0

(9.28a)

(9.28b)

and

(9.29a)

(9.29b)

Boundary conditions at x  L

(9.30a)

(9.30b)

and

(9.31a)

(9.31b)

0w¿



b a

0w–

xL

 0

w¿1L,t 2 0



b c

0w¿



0w–

b

xL

 0

w1L,t2 0

0w¿



b a

0w–

x0

 0

w¿10,t 2 0



b c

0w¿



0w–

b

x0

 0

w10,t2 0



0w¿

b

0w–

b

b

0x0t

b 0

552 CHAPTER 9 Vibrations of Beams

E. B. Magrab, Vibrations of Elastic Structural Members, Sijthoff & Noordhoff International

Publishing Co., The Netherlands, pp. 5–12 (1979).

9.2 Governing Equations of Motion 553

Equations (9.27) to (9.31) represent the general form of the equations of mo-

tion for beams subjected to conservative forces.

Nonconservative Systems

In the nonconservative case, the work done by the nonconservative force per

unit length f

(x,t) acting on the system in the continuum interior and the non-

conservative forces f

nc0

(t)  f

(0,t) and f

ncL

(t)  f

(L,t) acting at the bound-

aries x  0 and x  L, respectively, also need to be taken into account. In this

case, Eqs. (9.27) to (9.31) are modiﬁed to the following.

Continuum interior (0  x  L)

(9.32)

Equation (9.32) is referred to as the Lagrange differential equation of motion

for spatially one-dimensional continuous systems.

Boundary conditions at x  0

(9.33a)

(9.33b)

and

(9.34a)

(9.34b)

Boundary conditions at x  L

(9.35a)

(9.35b)



xL

 f

ncL

 0



b c

0w¿



0w–

w1L,t 2 0

0w¿



b a

0w–

x0

 0

w¿10,t 2 0



x0

 f

nc0

 0



b c

0w¿



0w–

w10,t 2 0



0x0t

b f

 0



0w¿

b

0w–

b

and

(9.36a)

(9.36b)

9.2.4 Beam Equation for a General Case

We now derive the governing equation for the beam considered in Section 9.2.1

and shown in Figure 9.5. This system consists of an external transverse load

f (x,t), which for purposes of generality is assumed to be composed of a con-

servative load and a nonconservative load. It is expressed as

(9.37)

where the conservative part is due to gravitational loading, as in Eq. (9.12b).

The load due to the spring foundation with stiffness k

per unit length is a con-

servative load, and, for convenience, the load due to the axial load p(x,t) is as-

sumed to be a conservative load. At the left boundary, there is a linear trans-

lation spring with stiffness k

and a linear torsion spring with stiffness k

Similarly, at the right boundary, there is a linear translation spring with stiff-

ness k

and a linear torsion spring with stiffness k

. There is also an inertia el-

ement with mass M

and rotary inertia J

at the left boundary and an inertia

element with mass M

and rotary inertia J

at the right boundary. There are

also linear viscous dampers with damping coefﬁcients c

at x  0 and c

x  L, respectively. Since the system is nonconservative, we will make use of

Eqs. (9.32) through (9.36) to derive the equations of motion and the bound-

ary conditions.

The functions G

, G

, and G

are given by Eqs. (9.19), (9.20), and (9.21),

respectively. Since we have viscous dampers at the boundaries, there are non-

conservative forces that are given by Eqs. (9.24); they are reproduced below.

(9.38)

On using Eq. (9.19) to evaluate the individual terms in Eq. (9.32), we arrive at

nc0

1t 2c

and

ncL

1t 2c

f 1x,t2 f

1x,t 2 f

1x,t 2

0w¿



b a

0w–

xL

 0

w¿1L,t 2 0

554 CHAPTER 9 Vibrations of Beams

x  0 x  L

, J

f(x, t)

p(x, t)

FIGURE 9.5

Beam on an elastic foundation, under

axial and transverse loads, and with

discrete elements at the boundaries.

(9.39)

After substituting Eqs. (9.39) into Eq. (9.32) and taking into account Eq.

(9.37), we obtain the governing equation of motion for the beam in 0  x  L:

(9.40)

Force per unit length due to Force per unit length due Force per unit Force per unit External

beam ﬂexural stiffness EI(x) to tensile axial force length due to length due to transverse

p(x,t) elastic foundation beam mass per loading per

with stiffness unit length rA(x) unit length

per unit area k

where

(9.41a)

External Conservative part Nonconservative

transverse of external part of external

loading per transverse transverse loading

unit length loading per per unit length

unit length

If the gravitational loading is the only conservative loading acting on the sys-

tem, then making use of Eqs. (9.12b) and (9.37), the transverse loading f(x,t)

is written as

(9.41b)

Furthermore, the conservative load due to gravity is a static load; that is, a

time-independent load. If distributed damping is present, where the associ-

ated damping coefﬁcient is c, then one possible form of this nonconservative

force is

(9.41c)

where the units of this term are force/length. The minus sign in Eq. (9.41c) in-

dicates that this loading opposes the motion. In Example 9.8, consideration of

such a term is illustrated.

The four boundary conditions are obtained as follows. The two boundary

conditions at x  0 are obtained by using Eqs. (9.19) and (9.20) in Eqs. (9.33)

1x,t 2c

f 1x,t 2 r1x 2A1x2g  f

1x,t 2

f 1x,t2



1x,t 2



1x,t 2

aEI1x 2

b

ap1x,t 2

b k

w1x,t 2 rA1x 2

 f 1x,t2

0x0t

b 0

b rA1x 2

0w–

b

aEI1x2

0w¿

b

ap1x,t2

k

w1x,t 2 f

9.2 Governing Equations of Motion 555

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

and (9.34), and the two boundary conditions at x  L are obtained by using

Eqs. (9.19) and (9.21) in Eqs. (9.35) and (9.36). Performing the indicated op-

erations, we obtain:

x  0

(9.42a)

(9.42b)

and

(9.43a)

(9.43b)

x  L

w(L,t)  0 (9.44a)

(9.44b)

and

w(L,t)  0 (9.45a)

(9.45b)

Referring to Figure 9.2, it is recalled that the quantity w is the slope of

the beam with respect to the x-axis or the rotation of the neutral axis of the

beam about the y axis. The shear force V and the bending moment M are pres-

ent in the boundary conditions as noted from Eqs. (9.8) and (9.9); that is,

(9.46)V 



aEI

M  EI

 J

0x0t

 EI1x 2

xL

 0

w  c

 M



aEI1x 2

b p

xL

 0

ck

 J

0x0t

 EI1x 2

x0

 0

w¿10,t 2 0

w  c

 M



aEI1x2

b p

x0

 0

w10,t 2 0

556 CHAPTER 9 Vibrations of Beams

9.2 Governing Equations of Motion 557

Thus, each of Eqs. (9.42b) and (9.44b) represents a force balance at an end of

the beam and each of Eqs. (9.43b) and (9.45b) represents a moment balance

at an end of the beam. From the boundary conditions given by Eqs. (9.42) to

(9.45), we see that if the magnitudes of the stiffness and inertia elements are

different from zero, then the displacement and the slope cannot be zero at ei-

ther end of the beam. Hence, in the general case, the four boundary conditions

for the system shown in Figure 9.5 are given by

x  0

(9.47a)

x  L

(9.47b)

From Eqs. (9.42) to (9.45), it is clear that the boundary conditions are,

in general, speciﬁed in terms of either displacement and/or force and either

slope and/or moment. Boundary conditions expressed only in terms of dis-

placement or slope are referred to as geometric boundary conditions, and

boundary conditions expressed in terms of shear force or bending moment are

referred to as dynamic boundary conditions. Therefore, boundary conditions

obtained through force balance and moment balance are dynamic boundary

conditions. The different boundary conditions, which are obtained from Eqs.

(9.47), are summarized in Table 9.1. In presenting these boundary conditions,

we have omitted the subscript convention employed so far to denote a speciﬁc

boundary. This convention should be included as appropriate, depending on

the boundary being considered.

To illustrate how the different boundary conditions in Table 9.1 are

obtained, consider the ﬁrst entry, which speciﬁes the boundary conditions

at a clamped end. One can write these boundary conditions directly from

geometry; that is, at a clamped end, the displacement and the slope are zero.

Alternatively, we consider Eqs. (9.47a) and divide the ﬁrst of Eqs. (9.47a) by

the translation stiffness k

and the second of Eqs. (9.47a) by the torsion stiff-

ness k

. The result is

c



0x0t



EI1x 2

x0

 0

cw 



aEI1x2

b

x0

 0

 J

0x0t

 EI1x 2

xL

 0

w  c

 M



aEI1x 2

b p

xL

 0

ck

 J

0x0t

 EI1x 2

x 0

 0

w  c

 M



aEI1x 2

b p

x0

 0

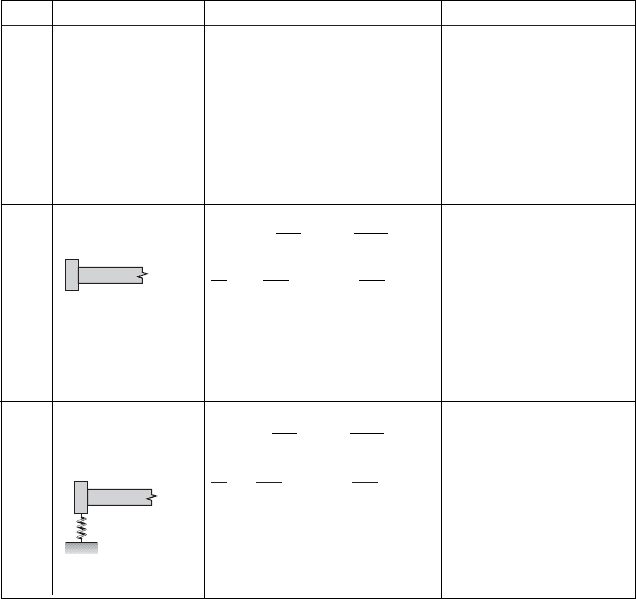
TABLE 9.1

Boundary Conditions

for Beams

Case Description Boundary Conditions Remarks

1 Clamped

2 Pinned

(hinged, simply

supported)

3 Free, with axial p is tensile. Replace p with p

force for a compressive force. For

no axial force, p  0.

Valid at either end of the beam.

4 Free, with massless Rigid constraint does not

rigid constraint permit rotation, but can

and axial force move unimpeded vertically.

p is tensile. Replace p with

p for a compressive force.

For no axial force, p  0.

Valid at either end of the beam.

5 Free, with a k: spring constant (no

translation spring resistance to torsion)

1 at x  0

1 at x  L

k → q; that is, w  0, Case 2

k  0; that is, (EIw)0,

Case 3 if p  0

6 Free, with a torsion k

: spring constant (no

spring resistance to vertical motion)

1 at x  0

1 at x  L

→ q; that is, w0,

Case 4 if p  0

 0; that is, w0,

Case 3 if p  0

7 Pinned, with a k

: spring constant (no

torsion spring resistance to vertical motion)

1 at x  0; s

1

at x  L

→ q; that is, w0,

Case 1

 0; that is, w0,

Case 2

8 Free, with torsion

k: spring constant (no

and translation

resistance to torsion)

springs

: spring constant (no

resistance to vertical motion)

1 at x  0; s

1

at x  L

aEI

b s

 s¿

 s

w  0

aEI

b 0

 s

aEI

b s

 0

aEI

b p

 0

aEI

b p

 0

w  0

 0

w  0

(continued)

Upon taking the limits and , these equations lead to the

boundary conditions given by Eqs. (9.42a) and (9.43a), respectively; that is,

the displacement is zero and the slope is zero. Similarly, if one were to use

Eqs. (9.47b) and considers the limits the translation stiffness and the

torsion stiffness , then we arrive at the boundary conditions given by

Eqs. (9.44a) and (9.45a). Thus, we can think of a clamped end as a boundary

with inﬁnite translation stiffness and inﬁnite rotation stiffness.

If we consider the boundary conditions for a pinned end, which is the sec-

ond entry of Table 9.1, this boundary is thought of as having inﬁnite transla-

tion stiffness and zero torsion stiffness and zero rotary inertia. In the case of

the free end without an axial force—that is, a special case of the third entry of

Table 9.1—we see that this boundary condition is thought of as having zero

translation stiffness, zero torsion stiffness, zero translation inertia, and zero

rotary inertia. In practice, most boundary conditions lie between the two lim-

iting cases; that is, between a free end and a ﬁxed end.

In Section 9.3, we examine the free oscillations of beams. Before doing

so, we make several simplifying assumptions to reduce the algebra in the de-

velopment. First, we assume that the beam is homogeneous and that it has a

uniform cross-section along its length; that is,

(9.48)EI1x 2 EI,

r1x 2 r,

and

A1x 2 A

씮 q

씮 qk

씮 q

9.2 Governing Equations of Motion 559

TABLE 9.1

(continued)

Case Description Boundary Conditions Remarks

8(continued) s

1 at x  0; s

1

at x  L

k → q; Case 7; k  0,

Case 6

 0; Case 5; k → q and

→ q, Case 1

→ q and k  0, Case 4

if p  0

9 Free, with mass M

: attached mass

attached J

: mass moment of inertia

of M

1 at x  0 s

1

at x  L

s

1 at x  0 s

1

at x  L

 0 and J

 0, Case 3

if p  0

10 Free, with mass and M

: attached mass

translation spring J

: mass moment of inertia

attached of M

k: spring constant (no

resistance to torsion)

1 at x  0; s

1

at x  L

s

1 at x  0 s

1

at x  L

aEI

b s¿

 s¿

 s

0x0t

aEI

b s¿

 s

0x0t