Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

540

Many types of elastic structures can be modeled as thin elastic beams. Towers, drills, and baseball bats are examples

of such systems. (Source: Kristiina Paul; © Jeffwilliams87 / Dreamstime.com)

541

Vibrations of Beams

9.1 INTRODUCTION

9.2 GOVERNING EQUATIONS OF MOTION

9.2.1 Preliminaries from Solid Mechanics

9.2.2 Potential Energy, Kinetic Energy, and Work

9.2.3 Extended Hamilton’s Principle and Derivation of Equations of Motion

9.2.4 Beam Equations for a General Case

9.3 FREE OSCILLATIONS: NATURAL FREQUENCIES AND MODE SHAPES

9.3.1 Introduction

9.3.2 Natural Frequencies, Mode Shapes, and Orthogonality of Modes

9.3.3 Effects of Boundary Conditions

9.3.4 Effects of Stiffness and Inertia Elements Attached at an Interior Location

9.3.5 Beams with an Interior Mass, Spring, and Single Degree-of-Freedom

System Attached Simultaneously

9.3.6 Effects of an Axial Force and an Elastic Foundation

9.3.7 Tapered Beams

9.4 FORCED OSCILLATIONS

9.5 SUMMARY

9.1 INTRODUCTION

In Chapters 3 through 8, vibrations of systems with ﬁnite degrees of freedom

were treated. As mentioned in Section 2.5, elements with distributed inertia

and stiffness properties, such as beams, are used to model many physical

systems such as the ski of Section 2.5.4, the work-piece-tool system of Section

2.5.5, and the MEMS accelerometer of Section 2.5.2. As noted previously,

distributed-parameter systems, which are also referred to as spatially continu-

ous systems, have an inﬁnite number of degrees of freedom. Apart from beams,

distributed systems that one could use in vibratory models include strings, ca-

bles, bars undergoing axial vibrations, shafts undergoing torsional vibrations,

membranes, plates, and shells. Except for the last three systems mentioned, the

descriptions of all of the other systems require one spatial coordinate. The

equations of motion, which govern vibratory systems with ﬁnite degrees of

freedom, are ordinary differential equations, and these equations are in the

form of an initial-value problem. By contrast, the equations of motion govern-

ing distributed-parameter systems are in the form of partial differential equa-

tions, with boundary condition and initial conditions, and the determination of

the solution for the vibratory response of a distributed-parameter system re-

quires the use of additional mathematical techniques. However, notions such as

natural frequencies, mode shapes, orthogonality of modes, and normal-mode

solution procedures used in the context of ﬁnite degree-of-freedom systems ap-

ply equally well to inﬁnite degree-of-freedom systems. An inﬁnite degree-of-

freedom system has an inﬁnite number of natural frequencies and a mode shape

associated with the free oscillations at each one of these frequencies.

In this chapter, the free and forced vibrations of beams are considered at

length. The oscillations of bars, shafts, and strings are treated in Appendix G.

As illustrated by the diverse examples of Section 2.5, vibratory models of

many physical systems require the use of beam elements. In addition to these

examples, other examples where beam elements are used to model physical

systems include models of rotating machinery, ship hulls, aircraft wings, and

vehicular and railroad bridges. Propeller blades in a turbine and the rotor

blades of a helicopter are modeled by using beam elements. Since the vibra-

tory behavior of beams is of practical importance for these different systems,

the focus of this chapter will be on beam vibrations.

In each of the applications cited above, and in many others, the beams are

acted upon by dynamically varying forces. Depending on the frequency con-

tent of these forces, the forces have the potential to excite the beam at one or

more of its natural frequencies. One of the frequent requirements of a design

engineer is to create an elastic structure that responds minimally to the imposed

dynamic loading, so that large displacement amplitudes, high stresses and

structural fatigue are minimized, and wear and radiated noise are decreased.

The governing equations of motion for beams are obtained by using the

mechanics of elastic beams and Hamilton’s principle. Free oscillations of un-

forced and undamped beams are treated and various factors that inﬂuence the

natural frequencies and modes are examined. This examination includes the

treatment of inertial elements and springs attached at an intermediate location

and beam geometry variation. The limitations of the models used in the pre-

vious chapters are also pointed out in the context of systems where a ﬂexible

structure supports systems with one or two degrees of freedom. The use of the

normal-mode approach to determine the forced response of a beam is also

presented.

In this chapter, we shall show how to:

• Determine the natural frequencies and mode shapes of Bernoulli-Euler

beams of constant cross-section for a wide range of boundary conditions.

• Determine the conditions under which the mode shapes are orthogonal for

the given mass and stiffness distributions.

542 CHAPTER 9 Vibrations of Beams

• Determine the natural frequencies and mode shapes of Bernoulli-Euler

beams with attached local stiffness and inertia elements.

• Determine the natural frequencies and mode shapes of Bernoulli-Euler

beams of variable cross-section.

• Determine the responses of Bernoulli-Euler beams to initial displacements,

initial velocities, and external forcing.

9.2 GOVERNING EQUATIONS OF MOTION

In this section, we illustrate how the governing equations of an elastic beam

undergoing small transverse vibrations are obtained for arbitrary loading con-

ditions and boundary conditions. A beam element in a deformed conﬁguration

is shown in Figure 9.1. The x-axis runs along the span of the beam, and the

y-axis and z-axis run along transverse directions to the x-axis. End moments of

magnitude M are shown acting along the j direction, and it is assumed that the

beam displacement is conﬁned to the x-z plane. The displacement w(x,t)

denotes the transverse displacement at a location along the beam.

The derivation of the governing equations of motion is based on the

extended Hamilton’s principle. To use this principle, one ﬁrst needs to deter-

mine the system potential energy, the system kinetic energy, and the work

done on the system. For determining the system kinetic energy, each element

of length x is treated like a rigid body and for determining the system

potential energy, stress-strain relationships in the beam material are used. To

this end, preliminaries from solid mechanics are presented in Section 9.2.1,

and then the expressions for the kinetic energy, potential energy, and work are

obtained in Section 9.2.2.

9.2.1 Preliminaries from Solid Mechanics

In Figure 9.1, it is seen that the face of the beam located toward the center of

curvature will be contracted while that on the opposite face will be extended;

that is, face AA will be extended, while the face BB will be contracted. The

line passing through the centroids of the cross-section of the beam is called

9.2 Governing Equations of Motion 543

Center line

(Neutral axis)



w(x, t)

s

–z

FIGURE 9.1

Deformation of a beam subjected to

end moments.

the central line. Here, a ﬁber along the central line is assumed to experience

zero axial strain. Hence, this central line is the neutral axis. The deformation

of the beam is assumed to be described by Bernoulli-Euler beam theory,

which is applicable to thin elastic beams whose length to radius of gyration

ratio is greater than 10. In keeping with this theory, it is assumed that the neu-

tral axis remains unaltered, that the plane sections of the beam normal to the

neutral axis remain plane and normal to the deformed central line, and that the

transverse normals such as BA experience zero strain along the

normal direction. For a ﬁber located at a distance z from the neutral axis, as

shown in Figure 9.1, the strain experienced along the length of the beam is

given by

(9.1)

where R is the radius of curvature, s

is the length of a ﬁber along the neu-

tral axis, s is the length of a ﬁber that is located at a distance z from the

neutral axis, and we have used geometry to write

(9.2)

From Hooke’s law, the corresponding axial stress s acting on the ﬁber is

(9.3)

where E is the Young’s modulus of the material. According to the convention

shown in Figure 9.l, a positive displacement w is in the direction of the unit

vector k. Therefore, the ﬁbers above the neutral axis experience a positive s,

which denotes tension, and the ﬁbers below the neutral axis experience a neg-

ative s, which denotes compression.

At an internal section of the beam, a moment balance about the y-axis

leads to

(9.4)

where y

and y

are the spatial limits corresponding to integration along the

y direction, we have used Eq. (9.3), and

(9.5)

The quantity I represents the area moment of inertia of the beam’s cross-

section about the y-axis, which is through the centroid. In general, the limits

of the double integral in Eq. (9.5) do not have to be constants; that is, a  a(x),

b  b(x), y

 y

(x), and y

 y

(x). In this case, the area moment of inertia

I 



a

dzdy

M 



a

szdzdy 

s  EP 

¢s  1R  z 2¢u

and

¢s

 R¢u

P 

¢s  ¢s

¢s



544 CHAPTER 9 Vibrations of Beams

E. P. Popov, Engineering Mechanics of Solids, Prentice Hall, Upper Saddle River, NJ, Chapter 6

(1990).

varies along the length, and therefore, in general, I  I(x). The curvature k 

1/R, which is assumed to be positive for concave curvature downwards, is

(9.6)

If it is assumed that the slope is small—that is, , where ∂w/∂x is

the slope of the neutral axis at location x—then Eq. (9.6) simpliﬁes to

(9.7)

Upon substituting Eq. (9.7) into Eqs. (9.1) and (9.4), we obtain

(9.8)

Thus, the magnitude of the strain and bending moment are proportional to the

second spatial derivative of the beam displacement. The statement that the

bending moment is linearly proportional to the second spatial derivative of

the beam displacement is the Bernoulli-Euler law, which is the underlying ba-

sis for the theory of linear elastic thin beams.

Equation (9.8) was obtained by considering only the effects of moments

on the ends of the beam. If, in addition, there is a transverse load f (x,t),

then there are vertical shear forces within the beam that resist this force. In

Figure 9.2, if the sum of the moments about point o is taken along the j direc-

tion, and if the rotary inertia of the beam element is neglected, the result is

which leads to

In the limit , the shear force increment , and we have

(9.9a)lim

¢x씮 0

¢M

¢x



 V

¢V 씮 0¢x 씮 0

¢M

¢x

 V  ¢V

M  1V  ¢V2¢x  M  ¢M

M  EI

P z

k 



00w/0x 0 1

k 



c1  a

3/2

9.2 Governing Equations of Motion 545

x

w

s

M M

V V

f(x, t)

FIGURE 9.2

Deformation of an element of a beam

subjected to a transverse load.

which, after making use of Eq. (9.8), results in

(9.9b)

Thus, the shear force is equal to the change of the bending moment along the

x-axis. Consequently, if M(x) is constant along x, then V  0.

9.2.2 Potential Energy, Kinetic Energy, and Work

We construct the system potential energy, the system kinetic energy, and

determine the work done by external forces for further use in Section 9.2.4.

Potential Energy

The potential energy of a deformed beam has contributions from different

sources, including the strain energy. For a beam undergoing axial strains due

to bending, if the strain energy is the only contribution to the system potential

energy, the beam’s potential energy is written as

(9.10)

where we have used Eqs. (9.1), (9.3), and (9.7).

Kinetic Energy

Assuming that the translation kinetic energy of the beam is the only contri-

bution to the system kinetic energy, one can write it as

(9.11)

where A  A(x) is the cross-sectional area of the beam and r  r(x) is

the mass density of the beam’s material. If the rotary inertia of the beam ele-

ment is also taken into account, an additional term corresponding to the rota-

tional kinetic energy will have to be included in Eq. (9.11), as described by

Eq. (1.23).

T1t 2



a



r a

dydzdx 



rA a





EI a

U1t 2



a



sPdydzdx 



a



dydzdx

V 



aEI

546 CHAPTER 9 Vibrations of Beams

See, for example, I. S. Sokolonikoff, Mathematical Theory of Elasticity, McGraw Hill, NY,

Chapters 1–3 (1956).

Since the symbol V is used for the shear force, the symbol U is used for the potential energy,

which differs from the notation used in the earlier chapters.

Work

The work done by the applied transverse conservative load per unit length

(x,t) is given by

(9.12a)

If gravity is the only distributed conservative load acting on the beam, then

(9.12b)

If the beam is also under the action of an axial tensile force

p(x,t), as shown

in Figure 9.3, then the length of the central line no longer remains constant,

but extends to a new length. If we assume that the deformation is small in

magnitude and does not affect the loading p(x,t), then the change in length of

an element of the beam is (s x) where

(9.13)

Therefore, the external work of the axial force is given by

(9.14)

where we have used Eq. (9.13). Since the tensile force acts to oppose the

beam transverse displacement w, the work done has a minus sign. If the axial

force is compressive, then p(x,t) is replaced by p(x,t).





p1x,t 2a

¢s  c1 

¢w

¢x

d¢x

1x,t 2 r1x2A1x 2g

1t 2



1x,t 2w1x,t2dx

9.2 Governing Equations of Motion 547

Axial loads are common in rotating blades, pipes with ﬂow, and structural columns.

Note that from geometry, we have

which leads to

For small slope—that is, 0w/x 0 1—this leads to

or equivalently,

To construct this integral, it is noted that the work done on a segment is p(x,t)(s x), the

limit is considered, and in this limit, x is replaced by dx.¢x 씮 0

¢s  ¢x 

¢w

¢x

¢s

¢x

 1 

¢w

¢x

¢s

¢x



1  a

¢w

¢x

¢s

 ¢w

 ¢x

p(x, t)

p(x x, t

)

x

FIGURE 9.3

Beam element under axial tensile

load and on an elastic foundation.

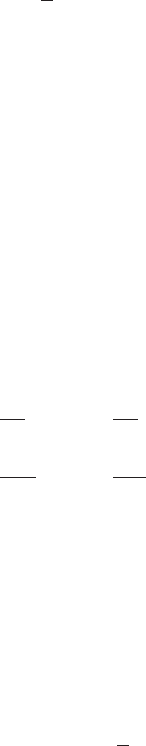
Finally, we consider the linear elastic foundation

on which the beam is

resting, as shown in Figure 9.3. The transverse displacement of the beam cre-

ates a force in the foundation with the magnitude f

(x,t)  k

w(x,t), where

is the spring constant per unit length of the foundation. This spring force

opposes the motion of the beam. The external work done by the elastic foun-

dation is

(9.15)

where, again, we have introduced a minus sign to account for the fact that the

foundation force acting on the beam opposes the beam displacement.

System Lagrangian

With the objective of constructing the system Lagrangian L

, we construct the

function G

(x,t,w,,w,,w) from the expression

(9.16)

where

(9.17)

and we have introduced the compact notation

(9.18)

In Eqs. (9.18), , w, , and w represent the beam velocity, beam slope,

beam angular velocity, and beam curvature, respectively. In Eq. (9.17), W

(t)

is the work done by conservative forces and it has been constructed assuming

that the work W

(t) done by the external loading f

(x,t) is conservative and that

the work W

(t) done by the axial loading p(x,t) is conservative.

After collecting the spatial integrals given by Eqs. (9.10), (9.11), (9.12a),

(9.14), and (9.15) for U(t), T(t), W

(t), W

(t), and W

(t), respectively, we ﬁnd

from Eq. (9.16) that

(9.19)G

1x,t,w,w

,w¿,w

¿,w– 2

3rAw

 EIw–

 pw¿

 k

4 f

¿w

w¿



0x0t

w– 



w¿ 

1t 2 W

1t 2 W

1t 2



1x,t,w,w

,w¿,w

¿,w– 2dx  T1t 2 U1t 2 W

1t 2

¿w

1t 2



1x,t 2dx

548 CHAPTER 9 Vibrations of Beams

This type of elastic foundation is frequently used to model structures on soil and it is often re-

ferred to as a Pasternak foundation.

Conservative forces were ﬁrst mentioned in Section 2.3, where it was noted that forces

expressed in terms of a potential function, such as a spring force or a gravity loading, are con-

servative. On the other hand, dissipative loads such as those due to dampers and time-dependent

loads such as harmonic excitations are nonconservative.

In Eq. (9.19), there is no term, since we have neglected the rotary inertia

of the beam cross-section in the development.

On the boundaries of the beam at x  0 and x  L, one can have discrete

external elements that contribute to the total kinetic energy and the total

potential energy of the system. Consider, for example, the beam shown in

Figure 9.4. At the left boundary (x  0), there is a linear translation spring

with stiffness k

and a linear torsion spring with stiffness k

. Similarly, at

the right boundary (x  L), there is a linear translation spring with stiffness k

and a linear torsion spring with stiffness k

. There is also an inertia element

with mass M

and rotary inertia J

at the left boundary and an inertia element

with mass M

and rotary inertia J

at the right boundary. There are also linear

viscous dampers with damping coefﬁcients c

at x  0 and c

at x  L. Tak-

ing the difference between the kinetic energy of the inertia element at the left

boundary and the potential energy of the stiffness elements at the left bound-

ary in Figure 9.4, we obtain the discrete Lagrangian function

(9.20)

Translational Rotational Potential Potential

kinetic energy kinetic energy energy of energy of

of rigid body of rigid body translation torsion spring

spring

where the subscript 0 has been used to denote that the quantity is evaluated at

x  0; that is, w

 w(0,t) indicates the displacement at the boundary x  0,

indicates the slope at the boundary x  0, and so on. Also,

the translational velocity of the center of mass of the rigid body is denoted as

, the angular displacement of the torsion spring is denoted as , and the an-

gular velocity of the rigid body is denoted as . Similarly, the discrete

Lagrangian function corresponding to the right boundary x  L is given by

(9.21)

Translational Rotational Potential Potential

kinetic energy kinetic energy energy of energy of

of rigid body of rigid body translation torsion spring

spring

where the subscript L has been used to denote that the quantity is evaluated at

x  L; that is, w

 w(L,t) indicates the displacement at the boundary x  L,

1t,w

,w¿

2





w¿

 0w10,t2/0x

1t,w

¿,w

¿ 2





9.2 Governing Equations of Motion 549

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

⎫

⎬

⎭

x  0 x  L

, J

FIGURE 9.4

Beam with discrete elements at the

boundaries.