Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


590 CHAPTER 9 Vibrations of Beams
distributed elastic spring. This is done by replacing the elastic foundation
term k
f
w(x,t)by
(9.106)
where d(x L
1
) is the delta function. Taking into account that the beam is uni-
form and homogeneous, Eq. (9.40) is written as
(9.107)
Mass Attached to an Interior Point x L
1
The governing equation of motion for the system shown in Figure 9.11b is ob-
tained from Eq. (9.40) by representing the discrete mass M
s
as a distributed
mass. This is done by replacing the mass density of the beam by
(9.108)
Then Eq. (9.40) is reduced to
(9.109)
Undamped Single Degree-of-Freedom System Attached to an
Interior Point x L
1
The governing equation of motion for the system shown in Figure 9.11c is ob-
tained from Eq. (9.40). If z(t) is the displacement of the mass M
s
about its
equilibrium position, then the term that represents the force per unit length of
the elastic foundation k
f
w(x,t) is replaced by
(9.110)
and Eq. (9.40) leads to
(9.111a)
The equation describing the motion of the single degree-of-freedom sys-
tem is obtained from Eq. (3.27), which is the equation of motion for a damped
single degree-of-freedom system subjected to a base excitation. Here, the
beam vibrations act as base excitation for the spring-mass system shown in
Figure 9.11c. Setting c 0 in Eq. (3.27) because damping is absent and rec-
ognizing that in the present context x(t) z(t) and y(t) w(L
1
,t), Eq. (3.27)
becomes
(9.111b)M
s
d
2
z1t 2
dt
2
k
s
z1t 2 k
s
w1L
1
,t2
EI
0
4
w
0x
4
k
s
L
3w1x,t2 z1t 24d1x L
1
2 rA
0
2
w
0t
2
0
k
f
w1x,t 2씮
k
s
L
3w1x,t2 z1t 24d1x L
1
2
EI
0
4
w
0x
4
cAr
M
s
L
d1x L
1
2d
0
2
w
0t
2
0
r 씮 r
M
s
AL
d1x L
1
2
EI
0
4
w
0x
4
k
s
L
w1x,t 2d1x L
1
2 rA
0
2
w
0t
2
0
k
f
w1x,t 2씮
k
s
L
w1x,t 2d1x L
1
2
9.3 Free Oscillations 591
Equations (9.111), together with the boundary conditions, represent the gov-
erning equations of motion for the system shown in Figure 9.11c.
We now proceed to obtain the solution of Eqs. (9.111) for the boundary
conditions shown in Figure 9.11c. It will then be shown that limiting cases of
this solution also describe the responses of the systems shown in Figures
9.11a and 9.11b. Since we are considering free oscillations, we follow the
procedure used in Section 9.3.2 and let
(9.112)
where G(t) is a harmonic function of the form given by Eq. (9.63). Upon sub-
stituting Eqs. (9.112) into Eqs. (9.111) and using the notation of Eqs. (9.67),
the spatial eigenvalue problem takes the form
(9.113)
(9.114)
where h x/L, h
1
L
1
/L,
(9.115)
and m
o
rAL is the mass of the beam. It is noted that K
s
is the nondimensional
spring constant and M
so
is the ratio of the mass of the single degree-of-freedom
system to the mass of the beam.
The natural frequency of the single degree-of-freedom system by itself is
which we can express in terms of a frequency coefficient
s
as
(9.116)
We now determine the characteristic equation from which the natural fre-
quency coefficient
n
is obtained by making use of Eqs. (9.113) and (9.114) and
the associated boundary conditions.
Upon substituting for Z
o
from Eq. (9.114) into Eq. (9.113), we obtain
(9.117)
where
(9.118)B12
M
so
4
1 M
so
4
/K
s
d
4
W1h 2
dh
4
B1 2W1h2d1h h
1
2
4
W1h 2 0
4
s
v
2
s
t
2
o
K
s
M
so
v
s
B
k
s
M
s
K
s
k
s
L
3
EI
,
M
so
M
s
m
o
,
and
4
rAv
2
L
4
EI
v
2
t
o
2
a1
M
so
K
s
4
bZ
o
W1h
1
2
d
4
W1h 2
dh
4
K
s
3W1h2 Z
o
4d1h h
1
2
4
W1h 2 0
z1t 2 Z
o
G1t 2
w1x,t 2 W1x 2G1t2

592 CHAPTER 9 Vibrations of Beams
When the mass of the single degree-of-freedom system M
s
0, then M
so
0
in Eq. (9.118) and, therefore, B() 0. In this case, Eq. (9.117) reduces to
Eq. (9.68), which describes a beam without the attached single degree-of-
freedom system.
Equation (9.117) has two limiting cases that are of interest. In order to
determine these two cases, we first rewrite Eq. (9.118) as
(9.119)
Beam carrying a mass at H H
1
When the translation spring stiffness
k
s
→ q, we have the case of a mass attached directly to the beam at h h
1
,
as shown in Figure 9.11b. Then, since K
s
→ q, Eq. (9.119) reduces to
(9.120)
Upon substituting Eq. (9.120) into Eq. (9.117), we obtain
(9.121)
which is what we would have obtained if we had used Eqs. (9.67), the first of
Eqs. (9.112), and Eq. (9.109).
Beam with a spring attached at H H
1
When the mass , we have
the case where one end of a spring is attached directly to the beam at h h
1
and the other end of the spring is fixed, as shown in Figure 9.11a. In this case,
since , Eq. (9.119) reduces to
(9.122)
Upon substituting Eq. (9.122) into Eq. (9.117), we obtain
(9.123)
which could have been obtained directly from Eq. (9.107) by using Eqs.
(9.67) and the first of Eqs. (9.112).
Solutions for Natural Frequencies and Mode Shapes
To solve Eq. (9.117), we take the Laplace transform of each term in
Eq. (9.117) and obtain
28
(9.124)
W‡102 B12W1h
1
2e
sh
1
4
W
~
1s 2
1
1s
4
4
2
3W102s
3
W¿102s
2
W–102
d
4
W1h 2
dh
4
K
s
W1h 2d1h h
1
2
4
W1h 2 0
B12K
s
M
so
씮 q
M
s
씮 q
d
4
W1h 2
dh
4
4
c1
M
s
m
o
d1h h
1
2dW1h2 0
B12 M
so
4
B12
4
c
1
M
so
4
K
s
d
1
28
For extensions of this solution and different solution methods see: M. Gürgöze, “On the eigen-
frequencies of a cantilever with attached tip mass and spring-mass system,” J. Sound Vibration,
Vol. 190, No. 2, pp. 149–162 (1996); J.-S. Wu and H.-M. Chou, “Free vibration analysis of a can-
tilever beam carrying any number of elastically mounted point masses with the analytical-and-
numerical-combined method,” J. Sound Vibration, Vol. 213, No. 2, pp. 317–332 (1998); and
M. Gürgöze, “On the alternative formulations of the frequency equation of a Bernoulli-Euler
beam to which several spring-mass systems are attached in-span,” J. Sound Vibration, Vol. 217,

9.3 Free Oscillations 593
where (s) is the Laplace transform of W(h). In arriving at Eq. (9.124), we
have made use of Eqs. (A.7) and (A.8) of Appendix A in the same manner as
we did in arriving at Eq. (9.78). In comparing Eq. (9.124) with Eq. (9.78),
the additional term in Eq. (9.124) that is due to the attachment of the spring-
mass system at h h
1
was obtained by making use of transform pair 5 from
Table A in Appendix A.
The terms W(0), W(h
1
), W(0), W(0), and W(0) are the displacement at
h 0, the displacement at h h
1
, the slope at h 0, the second derivative of
W(h) evaluated at h 0, and third derivative of W(h) evaluated at h 0, re-
spectively. These five quantities and the nondimensional frequency coefficient
represent the unknown quantities that need to be determined.
The inverse transform of the first four terms of the right-hand side of
Eq. (9.124) were previously determined in obtaining Eq. (9.79), and the in-
verse of the last term is determined from transform pairs 3 and 23 in Table A
of Appendix A. Thus, we arrive at
(9.125)
where u(h) is the unit step function and the spatial functions Q(h), R(h),
S(h), and T(h) are given by Eqs. (9.80). To determine the six unknown
quantities, we make use of the boundary conditions and the fact that Eq.
(9.125) is valid at h h
1
. Making use of these five equations, we can at best
solve for and four of the other five unknown quantities.
Characteristic Equation and Mode Shapes
The boundary conditions for the beam systems shown in Figure 9.11 follow
from Eqs. (9.69) if we set J
o
M
o
0. Thus, the boundary conditions at
h 0 are
(9.126a)
and those at h 1 are
(9.126b)
where the prime () denotes the derivative with respect to h and the non-
dimensional quantities B
j
and K
j
are given by Eqs. (9.67). Upon substituting
Eqs. (9.126a) into Eq. (9.125), we obtain
(9.127)
B1 2W1h
1
2T13h h
1
42u1h h
1
2/
3
3R1h2/B
1
S1h 2/
2
4W¿10 2
W1h 2 3Q1h2 K
1
T1h 2/
3
4W102
W‡11 2 K
2
W11 2
W–11 2B
2
W¿11 2
W‡10 2K
1
W10 2
W–10 2 B
1
W¿10 2
W‡102T1h 2/
3
B1 2W1h
1
2T13h h
1
42u1h h
1
2/
3
W1h 2 W10 2Q1h2 W¿10 2R1h2/W–102S1h 2/
2
W
~
No. 3, pp. 585–595 (1998); K. Alsaif and M. A. Foda, “Vibration Suppression of a Beam Struc-
ture by Intermediate Masses and Springs,” J. Sound Vibration, Vol. 256, No. 4, pp. 629-645 (2002).
For the analysis of a beam supported by two interior springs, see C. Y. Wang, “Fundamental Fre-
quency of a Beam on Two Elastic Supports,” J. Sound Vibration, Vol. 259, pp. 711–714 (2003).

We now substitute Eq. (9.127) into the boundary conditions at h 1,
which are given by Eq. (9.126b), and perform the indicated operations to ob-
tain the following two equations in the unknowns W(0) and W(0).
(9.128)
In Eqs. (9.128),
(9.129a)
and
(9.129b)
Solving Eq. (9.128) for W(0) and W(0) yields
(9.130)
where
(9.131)
Upon substituting Eq. (9.130) into Eq. (9.127), we arrive at
(9.132)
where
(9.133)
Equation (9.132) must be valid at h h
1
. Therefore, setting h h
1
in Eq. (9.132), noting that T(0) 0 from Eqs. (9.80), we obtain the charac-
teristic equation for a uniform beam carrying an undamped single degree-of-
freedom system for the boundary conditions given by Eqs. (9.126):
(9.134)B12H
1
1h
1
,2
3
0
3R1h2 b
1
S1h 24h
2
1 2/D
o
1 2
H
1
1h, 23Q1h2 a
1
T1h 24h
1
1 2/D
o
1 2
W1h 2
B12W1h
1
2
3
1H
1
1h, 2 T 13h h
1
42u1h h
1
22
D
o
1 2 A
11
1 2A
22
1 2 A
12
1 2A
21
1 2
h
2
1 2 A
11
1 2E
2
1 2 A
21
1 2E
1
1 2
h
1
1 2 A
22
1 2E
1
1 2 A
12
1 2E
2
1 2
W¿10 2
B12W1h
1
2
D
o
1 2
2
h
2
1 2
W10 2
B12W1h
1
2
D
o
1 2
3
h
1
1 2
a
j
K
j
3
and
b
j
B
j
j 1, 2
E
2
1 2 a
2
T131 h
1
42 Q1 31 h
1
42
E
1
1 2 R131 h
1
42 b
2
S131 h
1
42
A
22
1 2 11 a
2
b
1
2S12 b
1
T12 a
2
R12
A
21
1 2 R12 1a
1
a
2
2Q12 a
1
a
2
T12
A
12
1 2 T 12 1b
1
b
2
2Q12 b
1
b
2
R12
A
11
1 2 11 a
1
b
2
2S12 a
1
R12 b
2
T12
A
21
1 2W102 A
22
1 2W¿10 2 B1 2W1h
1
2E
2
1 31 h
1
42/
2
A
11
1 2W102 A
12
1 2W¿10 2B1 2W1h
1
2E
1
1 31 h
1
42/
2
594 CHAPTER 9 Vibrations of Beams

where H
1
(h,) is given by Eq. (9.133). The values of that satisfy Eq. (9.134)
are the natural-frequency coefficients
n
. As mentioned previously, when
M
s
0, B() 0. Therefore, after substituting for H
1
(h
1
,) from Eq. (9.133),
multiplying Eq. (9.134) by D
o
(), and setting B() 0, we obtain
(9.135)
which, upon expansion, is identical to the characteristic equation given by
Eq. (9.85) with M
o
J
o
0.
For the system shown in Figure 9.11c, the mode shape associated with
the nondimensional frequency coefficient
n
is given by
(9.136)
where, for convenience, we have normalized the mode shape to remove the
arbitrary constant W(h
1
); that is,
From Eq. (9.137), the modal displacement of the mass M
s
is
(9.137)
Orthogonality of the Modes
We now determine if the mode shape given by Eq. (9.136) is an orthogonal
function in the sense of Eq. (9.66). We start with Eq. (9.117) and replace W(h)
with W
n
(h) and with
n
. Then, following the procedure used to obtain
Eq. (9.72) through Eq. (9.77), we arrive at
(9.138)
Since Eq. (9.138) is not symmetric in W
n
(h) and W
m
(h) as in Eq. (9.76), it can-
not be put in the form of Eq. (9.66). Hence, W
n
(h) is not an orthogonal func-
tion and, therefore, for a beam system with a spring-mass system attached at
an interior point, the modes do not form an orthogonal set.
When —that is, we have a system with a spring directly attached
to the beam at h h
1
as shown in Figure 9.11a—we find from Eq. (9.122)
that B(
n
) B(
m
) K
s
and Eq. (9.138) reduces to
(9.139)1
4
m
4
n
2
1
0
W
m
1h 2W
n
1h 2dh 0
M
s
씮 q
1B1
m
2 B1
n
22W
m
1h
1
2W
n
1h
1
2 0
1
4
m
4
n
2
1
0
W
m
1h 2W
n
1h 2dh
Z
on
W
n
1h
1
2a1
M
so
K
s
4
n
b
1
W
n
1h 2
W1h 2
B1
n
2W1h
1
2/
3
n
W
n
1h 2 H
1
1h,
n
2 T 1
n
3h h
j
42u1h h
j
2
D
o
1
n
2 0
9.3 Free Oscillations 595
which leads to
(9.140a)
where d
nm
is the Kronecker delta and
(9.140b)
Since W
n
(h) and h are nondimensional quantities, N
n
is a nondimensional
quantity. Thus, the mode shapes for a system where a translation spring is di-
rectly attached to a beam form an orthogonal set.
When ; that is, we have a system with a mass directly attached to
the beam at h h
1
as shown in Figure 9.11a, we find from Eq. (9.120) that
and Eq. (9.138) reduces to
(9.141)
which leads to
(9.142a)
where
(9.142b)
Thus, the mode shapes for a mass directly attached to a beam are orthogonal
functions.
We now examine Eq. (9.134) for three different types of boundary con-
ditions: (1) beam pinned at each boundary; (2) beam clamped at each bound-
ary; and (3) beam clamped at one end and free at the other end (cantilever).
Each of these sets of results is valid for the case of a beam with an attached
single degree-of-freedom system at h h
1
, a spring h h
1
, or a mass at
h h
1
. For the three cases shown in Figure 9.11c, Figure 9.11b, and Figure
9.11a, the expression for B() is given by Eq. (9.118), Eq. (9.120), and
Eq. (9.122), respectively, To specialize the general results for each set of
boundary conditions, we follow the procedure given in Section 9.3.3 by tak-
ing the limit as a
jn
and b
jn
go to either zero or infinity.
N
n
1
0
W
2
n
1h 2dh M
so
W
2
n
1h
1
2
1
0
W
m
1h 2W
n
1h 2dh M
so
W
m
1h
1
2W
n
1h
1
2 d
nm
N
n
1
4
m
4
n
2c
1
0
W
m
1h 2W
n
1h 2dh M
so
W
m
1h
1
2W
n
1h
1
2d 0
B1
n
2 M
so
n
4
K
s
씮 q
N
n
1
0
W
2
n
1h 2dh
1
0
W
m
1h 2W
n
1h 2dh d
nm
N
n
596 CHAPTER 9 Vibrations of Beams

Beam pinned at each boundary For this case, the boundary conditions cor-
respond to
(9.143)
Then Eq. (9.134), the characteristic equation in the general case, reduces to
(9.144)
where
n
is a root of the characteristic equation and
(9.145)
From Eq. (9.136), the corresponding mode shape of the beam is given by
(9.146)
Beam clamped at each boundary For this case, the boundary conditions are
obtained by setting
(9.147)
Then Eq. (9.134), the characteristic equation in the general case, reduces to
(9.148)
where
n
is a root of the characteristic equation and
(9.149)
From Eq. (9.136), the corresponding mode shape is given by
(9.150)
Beam clamped at one end and free at the other end (cantilever) For this
case, the boundary conditions are obtained by setting
(9.151)
Then Eq. (9.134), the characteristic equation in the general case, reduces to
(9.152)B1
n
23C
5n
T 1
n
h
1
2 C
6n
S1
n
h
1
24
3
n
0
h 1:
a
2n
0
and
b
2n
0
h 0:
a
1n
씮 q
and
b
1n
씮 q
W
n
1h 2 C
3n
T 1
n
h2 C
4n
S1
n
h2 T 1
n
3h h
1
42u1h h
1
2
C
4n
T
1
n
2S1
n
31 h
1
42 S1
n
2T 1
n
31 h
1
42
S
2
1
n
2 R1
n
2T 1
n
2
C
3n
R1
n
2T 1
n
31 h
1
42 S1
n
2S1
n
31 h
1
42
S
2
1
n
2 R1
n
2T 1
n
2
B1
n
23C
3n
T 1
n
h
1
2 C
3n
S1
n
h
1
24
3
n
0
h 1:
a
2n
씮 q
and
b
2n
씮 q
h 0:
a
1n
씮 q
and
b
1n
씮 q
W
n
1h 2 C
1n
T 1
n
h2 C
2n
R1
n
h2 T 1
n
3h h
1
42u1h h
1
2
C
2n
T
1
n
2R1
n
31 h
1
42 R1
n
2T 1
n
31 h
1
42
R
2
1
n
2 T
2
1
n
2
C
1n
T
1
n
2T 1
n
31 h
1
42 R1
n
2R1
n
31 h
1
42
R
2
1
n
2 T
2
1
n
2
B1
n
23C
1n
T 1
n
h
1
2 C
2n
R1
n
h
1
2
3
n
4 0
h 1: a
2n
씮 q
and
b
2n
0
h 0: a
1n
씮 q
and
b
1n
0
9.3 Free Oscillations 597

where
n
is a root of the characteristic equation and
(9.153)
From Eq. (9.136), the corresponding mode shape is
(9.154)
Equation (9.152) is also valid at ; that is, when the single degree-
of-freedom system is attached to the free end of the beam. In this case, since
R(0) 0 and Q(0) 1, Eq. (9.152) reduces to
(9.155)
We now present some numerical results for several types of in-span at-
tachments and three sets of boundary conditions: cantilever, hinged at both
ends, and clamped at both ends.
Beams with in-span spring K
s
For the cantilever beam, we substitute
Eq. (9.122) into Eq. (9.152) and use the resulting expression to obtain the
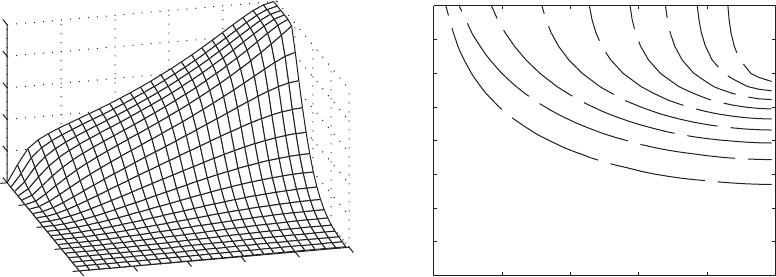
surface shown in Figure 9.12. In Figure 9.12a, we see that the lowest natural-
frequency coefficient reaches a peak value of when K
s
100
(i.e., when log
10
(K
s
) 2) and h
1
is around 0.8. From Case 4 of Table 9.3, we
see that a cantilever beam without attachments has a second natural frequency
of
1
/p 1.494 with a node point at h 0.783. Therefore, by placing a rela-
tive stiff spring at or near the node point of this second natural frequency, one
1
/p 1.49
B1
n
23S1
n
2R1
n
2 T1
n
2Q1
n
24
3
n
3Q
2
1
n
2 R1
n
2T1
n
24 0
h 1
W
n
1h 2 C
5n
T 1
n
h2 C
6n
S1
n
h2 T 1
n
3h h
1
42u1h h
1
2
C
6n
R1
n
2Q1
n
31 h
1
42 Q1
n
2R1
n
31 h
1
42
Q
2
1
n
2 R1
n
2T1
n
2
C
5n
T
1
n
2R1
n
31 h
1
42 Q1
n
2Q1
n
31 h
1
42
Q
2
1
n
2 R1
n
2T 1
n
2
598 CHAPTER 9 Vibrations of Beams
0
0.2
0.4
0.6
(
a
)
0.8
1
0
1
2
3
4
0.5
1
1.5
1
log
10
(K
s
)
Ω
1
/
(
b
)
1
0.6
0.6
0.6
0.7
0.7
0.7
0.7
0.8
0.8
0.8
0.9
0.9
0.9
1
1
1
1.1
1.1
1.1
1.2
1.2
1.3
1.3
1.3
1.4
1.4
1.4
log
10
(K
s
)
0 0.2 0.4 0.6 0.8 1
0
0.5
1
1.5
2
2.5
3
3.5
4
FIGURE 9.12
(a) Variation of the lowest natural-frequency coefficient of a cantilever beam restrained by a spring K
s
attached at h
1
and
(b) contour curves of constant values of the lowest natural-frequency coefficient of surface in (a).
effectively creates a system whose lowest natural frequency is now equal to that
of the second natural frequency of a cantilever beam without attachments. This
is accomplished because the beam is forced to assume the mode shape asso-
ciated with the second natural frequency of the beam without attachments.
However, when K
s
40 (i.e., when log
10
(K
s
) 1.6), the maximum natural fre-
quency is obtained by placing the spring at the free end of the beam.
From the contour curves shown in Figure 9.12b, we see that certain nat-
ural frequencies can be obtained from a range of combinations of the values
of K
s
and h
1
. For example, a value of can be attained for K
s
and
h
1
having the range of values: 10
0.5
K
s
10
4
and 0.3 h
1
1. We also
note that as the spring is placed closer to the free end of the beam, the mag-
nitude of K
s
that is required to maintain a constant frequency decreases. How-
ever, when h 0.8 and K
s
10
1.7
50, this is no longer true.
Next, we consider a beam hinged at both ends. For this case, we substi-
tute Eq. (9.122) in Eq. (9.144) and use the resulting expression to obtain the
surface shown in Figure 9.13. In Figure 9.13a, we see that the lowest natural-
frequency coefficient reaches a peak of when the K
s
10
3
(i.e.,
when log
10
(K
s
) 3) and h
1
0.5. From Case 2 of Table 9.3, we see that a
hinged-hinged beam without attachments has a second natural frequency of
with a node point at h 0.500. Therefore, by placing a stiff
spring at or near the node point of this second natural frequency, one effec-
tively creates a system whose lowest natural frequency is equal to that of the
second natural frequency of a beam without attachments. This is accom-
plished because the beam is forced to assume the mode shape of second nat-
ural frequency of the beam without attachments.
1
/p 2.00
1
/p 2
1
/p 0.7
9.3 Free Oscillations 599
0
0.1
0.2
0.3
0.4
0.5
0
1
2
3
4
1
1.2
1.4
1.6
1.8
2
Ω
1
/
log
10
(K
s
)
1
1.1
1.1
1.1
1.1
1.2
1.2
1.2
1.2
1.3
1.3
1.3
1.4
1.4
1.4
1.5
1.5
1.6
1.6
1.7
1.7
1.8
1.9
log
10
(K
s
)
0 0.1 0.2 0.3 0.4 0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
1
(a) (b)
FIGURE 9.13
(a) Variation of the lowest natural-frequency coefficient of a hinged-hinged beam restrained by a spring K
s
attached at h
1
and
(b) contour curves of constant values of the lowest natural-frequency coefficient of surface in (a). Note: Because the boundary
conditions are symmetric, we only need to consider the region 0 h
1
0.5.
