Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


Ω
s
2
Ω
2
M,1
Ω
1
2
Ω
2
2
0
5
10
15
20
25
30
Ω
2
M
so
4
M
so
1
M
so
0.3
M
so
0.3
M
so
1
M
so
4
10
1
10
0
o
10
0.78
(a)
2
4
6
8
10
12
14
16
18
20
22
Ω
s
2
Ω
2
M,1
Ω
1
2
Ω
2
2
Ω
2
M
so
4
M
so
1
M
so
0.3
M
so
0.3
M
so
1
M
so
4
10
1
10
0
o
10
0.78
(b)
FIGURE 9.29
Lowest two natural-frequency coefficients for a hinged-hinged beam carrying a mass and a single degree-of-freedom system at the
same location: (a) h
1
0.5 and (b) h
1
0.35.
0
1
2
3
4
5
6
7
8
9
10
Ω
s
2
Ω
2
M,1
Ω
1
2
Ω
2
2
Ω
2
M
so
4
M
so
4
M
so
1
M
so
1
M
so
0.3
M
so
0.3
10
1
10
0
o
10
0.48
(a)
0
2
4
6
8
10
12
Ω
s
2
Ω
2
M,1
Ω
1
2
Ω
2
2
Ω
2
M
so
4
M
so
4
M
so
1
M
so
1
M
so
0.3
M
so
0.3
10
1
10
0
o
10
0.48
(b)
FIGURE 9.30
Lowest two natural-frequency coefficients for a cantilever beam carrying a mass and a single degree-of-freedom system at the same
location: (a) h
1
1.0 and (b) h
1
0.7.
stiffness k
s
. Therefore, we can use Eq. (7.47) with k
23
0 to describe this two
degree-of-freedom system. To place Eq. (7.47) in the present notation, we use
Eqs. (7.41), (9.67) and (9.172) and obtain
(9.199)
In Eq. (9.199), K
beam
k
beam
L
3
/(EI) a; recall Eq. (9.157). If v
1,2
are the
natural frequencies of the two-degree-of-freedom system, then the natural
frequencies given by Eq. (7.47) can be written as
(9.200)
where
and from Eq. (7.46)
(9.201)
since we have chosen
s
beam
. Upon using Eq. (9.199) in Eq. (9.200), we
obtain
(9.202)
Thus, the percentage error between the exact natural frequency obtained
from Eq. (9.196) and those obtained from Eq. (9.202) is
(9.203)
A numerical evaluation of Eq. (9.203) is used to determine the minimum
value of g
o
for which e
1,2
5% for three sets of boundary conditions and
three values of M
so
, The results are shown in Table 9.9. It is seen from the table
that the values of g
o
needed to keep the error of the second natural frequency
less than 5% are always much greater than those required to keep the first nat-
ural frequency less than 5%. It is mentioned that the errors increase rapidly
for values that are less than the values given in the table.
e
1,2
100 a
2
2dof,1,2
2
1,2
1 b
%
2
1,2
2
2dof,1,2
B
a
2g
o
a2
M
so
g
o
A
M
so
g
o
a
4
M
so
g
o
b
b
a
2
v
2
r
4
s
4
beam
1
a
1
1 v
2
r
11 m
r
2 1
4
s
4
beam
a1
M
so
g
o
b 2
M
so
g
o
2
2dof,1,2
v
1,2
t
o
2
2dof,1,2
2
beam
20.51a
1
1a
2
1
4a
2
2
m
r
M
s
M
o
M
s
/m
o
M
o
/m
o
M
so
g
o
v
r
v
n2
v
n1
2
s
2
beam
v
n2
B
k
s
M
s
1
t
o
B
K
s
M
so
2
s
t
o
v
n1
B
k
beam
M
o
1
t
o
B
K
beam
g
o
2
beam
t
o
9.3 Free Oscillations 621
EXAMPLE 9.4 Natural frequencies of two cantilever beams connected by a spring:
bimorph grippers
Consider the two identical beams shown in Figure 9.31, each with the same
general boundary conditions. Each beam is carrying a mass M
o
at x L
1
. At-
tached to each of these masses is a spring of stiffness k
o
. We shall determine
the natural frequencies of this coupled system. If we assume that the beams
are undergoing harmonic vibrations, then the equations of motion for each of
these beams can be obtained directly from Eqs. (9.166) as
(a)
where
Upon taking the Laplace transform of Eqs. (a), we obtain
(b)
where is the Laplace transform of W
j
(h), j 1, 2 and
(c)P
21
1g
o
4
K
o
2W
2
1h
1
2 K
s
W
1
1h
1
2
P
12
1g
o
4
K
o
2W
1
1h
1
2 K
s
W
2
1h
1
2
W
ˆ
j
1s 2
W
ˆ
2
1s 2
1
s
4
4
3W
2
10 2s
3
W ¿
2
10 2s
2
W–
2
10 2s W‡
2
10 2 P
21
e
h
1
s
4
W
ˆ
1
1s 2
1
s
4
4
3W
1
10 2s
3
W¿
1
10 2s
2
W–
1
10 2s W‡
1
10 2 P
12
e
h
1
s
4
h
1
L
1
L
,
g
o
M
o
m
o
,
and
K
o
k
o
L
3
EI
d
4
W
2
1h 2
dh
4
4
31 g
o
d1h h
1
24W
2
1h 2 K
o
3W
2
1h 2 W
1
1h 24d1h h
1
2 0
d
4
W
1
1h 2
dh
4
4
31 g
o
d1h h
1
24W
1
1h 2 K
o
3W
1
1h 2 W
2
1h 24d1h h
1
2 0
622 CHAPTER 9 Vibrations of Beams
Clamped-Clamped (H
1
0.5) Hinged-Hinged (H
1
0.5) Clamped-Free (H
1
1.0)
M
so
0.3 g
o
4.1 g
o
5.3 g
o
3.1 g
o
4.2 g
o
1.9 g
o
2.7
1.0 g
o
3.5 g
o
5.9 g
o
2.5 g
o
4.5 g
o
1.4 g
o
3.0
4.0 g
o
2.0 g
o
6.6 g
o
1.1 g
o
5.2 g
o
1.0 g
o
3.5
2
2
dof,2
2
2
dof,1
2
2
dof,2
2
2
dof,1
2
2
dof,2
2
2
dof,1
TABLE 9.9
Values of M
so
and g
o
for which e
1,2
5%.

We assume that at h 0 each beam is restrained by a torsion spring of stiff-
ness k
tL
and a translation spring of stiffness k
L
. Then, the boundary conditions
at h 0 are
(d)
At the end h 1, we assume that each beam is restrained by a torsion spring
of stiffness k
tR
and a translation spring of stiffness k
R
. In addition, a mass M
R
is attached. Then, the boundary conditions at h 1 are
(e)
where the constants appearing in Eqs. (d) and (e) are given in Eqs. (9.67) and
in the equations following Eqs. (9.170) and (9.171).
We note that each of Eqs. (b) is the same as Eq. (9.173) if, in Eq. (9.173),
we let F
2
F
3
0 and set F
1
W(h
1
) P
12
. Also, the boundary conditions on
each beam are the same as those that were used to go from Eq. (9.173) to the
solution given by Eq. (9.181). Therefore, we can write the solutions to Eqs. (a)
subject to the general boundary conditions Eqs. (d) and (e) as
(f)W
2
1h 2
P
21
3
3H
1
1h, 2 T 1 3h h
1
42u1h h
1
24
W
1
1h 2
P
12
3
3H
1
1h, 2 T 1 3h h
1
42u1h h
1
24
W‡
j
11 2 aK
R
M
R
4
m
o
bW
j
11 2
j 1,2
W–
j
11 2K
tR
W¿
j
11 2
W‡
j
10 2K
L
W
j
10 2
j 1,2
W–
j
10 2 K
tL
W¿
j
10 2
9.3 Free Oscillations 623
FIGURE 9.31
Two beams each beam carrying a mass that is interconnected by a translational spring.
k
L
k
L
k
R
M
R
M
R
k
tL
k
tL
k
tR
k
R
k
tR
L
1
w
1
w
2
L
M
o
M
o
k
o

where H
1
(h,) is given by Eq. (9.182).
To obtain the frequency equation, we note that Eqs. (f) must be valid at
h h
1
. Therefore, Eqs. (f) become
(g)
since T(0) 0. We now substitute Eqs. (c) into Eqs. (g) and collect terms to
obtain
(h)
where
(i)
The frequency equation is obtained by setting the determinant of the coeffi-
cients of W
j
(h
1
) to zero. This leads to
(j)
The values of
n
that satisfy Eq. ( j) are the natural-frequency coeffi-
cients. We see from Eq. ( j) that the
n
are obtained from two independent
equations: a 0 and a 2b 0. The former equation is identical to
Eq. (9.134) when we set B() g
o
4
in Eq. (9.134). This equation gives the
natural-frequency coefficients corresponding to the case where the beams’
mode shapes are in-phase with the each other. This effectively has the inter-
connecting spring undergoing no net extension or compression. This type of
motion is a direct consequence of the two beams having identical geometric
and physical properties and having identical boundary conditions.
The solutions to the latter equation give the
n
for coupled system; that is,
(k)
The coupled motions correspond to the case where the beam’s mode shapes
are out-of-phase with each other. Equation (k) is the same as Eq. (9.196) when
we set B(
n
) 0 in Eq. (9.196) and let 2K
o
K
2
. The factor of two is due to
the fact that the spring of stiffness k
o
undergoes an extension or a compres-
sion at each of its ends whereas the spring k
2
undergoes an extension or com-
pression at only one end; its other end is fixed.
It should be noted that Eq. (k) is the solution for general boundary con-
ditions. We shall now use these results to approximate the case of a bimorph
3
n
1g
o
4
n
2K
o
2H
1
1h
1
,
n
2 0
a1a 2b 2 0
b
H
1
1h
1
,2
3
K
o
a 1 g
o
H
1
1h
1
,2
c
a b b
ba b
de
W
1
1h
1
2
W
2
1h
1
2
f 0
W
2
1h
1
2
P
21
3
H
1
1h
1
,2
W
1
1h
1
2
P
12
3
H
1
1h
1
,2
624 CHAPTER 9 Vibrations of Beams

gripper.
31
We assume that the beam is a cantilever beam and the mass and the
interconnecting spring are attached at the free end; that is, at h
1
1. To con-
vert these general results to those for a cantilever beam, we use the limiting
procedure discussed in Section 9.9.3 and find that
(l)
where C
5n
and C
6n
are given by Eq. (9.153). When h
1
1, C
5n
and C
6n
be-
come, respectively
(m)
since Q(0) 1 and R(0) 0. Therefore, the frequency equation is
(n)
Upon using Eqs. (9.80), we find that Eq. (n) can be written as
(o)
If we replace 2K
s
with K
2
, then Eq. (o) is identical to Eq. (10a) in Table 9.2.
The mode shapes are
(p)
In Eq. (p), we have set the scale factor
9.3.6 Effects of an Axial Force and an Elastic Foundation
on the Natural Frequency
32
We shall determine the effects that an axial force p(x,t) and an elastic foundation
k
f
have on the natural frequency coefficient. Axial forces arise in beam models of
many vibratory systems including rotating machinery, where the centrifugal
P
12
/
3
1.
W
jn
1h 2 H
1
1h, 2
j 1,2
3
n
11 cosh1
n
2cos1
n
22 0
1g
o
4
n
2K
s
23sin1
n
2cosh1
n
2 sinh1
n
2cos1
n
24
3
n
1Q
2
1
n
2 R1
n
2T1
n
22 0
1g
o
4
n
2K
s
23R1
n
2S1
n
2 Q1
n
2T 1
n
24
C
6n
R1
n
2
Q
2
1
n
2 R1
n
2T1
n
2
C
5n
Q1
n
2
Q
2
1
n
2 R1
n
2T1
n
2
H
1
1h,
n
2 C
5n
T1
n
h2 C
6n
S1
n
h2
9.3 Free Oscillations 625
31
S. Chonan, Z.W. Jaing, and M. Koseki, “Soft-Handling Gripper Driven by Piezoceramic
Bimorph Strips”, Smart Materials Structures, Vol. 5 (1996) pp. 407–414.
32
For a more compete treatment of this topic, see the following: F. J. Shaker, “Effect of Axial Load on
Mode Shapes and Frequencies of Beams,” Lewis Research Center Report NASA TN D-8109
(December 1975); G. C. Nihous, “On the continuity of the boundary value problem for vibrating free-
free straight beams under axial load,” J. Sound Vibration, Vol. 200, No. 1, pp. 110–119 (1997); and
M. A. De Rosa and M. J. Maurizi, “The influence of concentrated masses and Pasternak soil on the free
vibrations of Euler beams—exact solution,” J. Sound Vibration, Vol. 212, No. 4, pp. 573–581 (1998).
For an example of an axial force in a MEMS application, see A. Singh, R. Mukherjee, K. Turner,
and S. Shaw, “MEMS Implementation of Axial and Follower End Forces,” J. Sound Vibration,
Vol. 286, pp. 637–644 (2005).

forces are the source of the axial forces or in vertical structures such as water
towers. If we assume that p(x,t) p
o
is a constant and that the beam has a uniform
cross-section and uniform material along its length, then Eq. (9.40) is written as
(9.204)
where p
o
is a tensile force. Following the procedure used in Section 9.3.3, we
assume that the externally applied transverse load is zero—that is, f (x,t) 0
—and that the displacement is of the form given by Eq. (9.58). Then,
Eq. (9.204) leads to the spatial equation
(9.205)
where we have employed the notation of Eq. (9.67) and introduced the
quantities
(9.206)
Pinned-Pinned Beam
Rather than find a general solution to Eq. (9.205), we shall only obtain the so-
lution to a beam that is pinned at each of its ends. This will be sufficient for
us to illustrate the effects that p
o
and k
f
have on the natural frequency coeffi-
cient. From Eq. (2b) of Table 9.2 and Case 2 of Table 9.3, the spatial function
that satisfies the boundary conditions for a beam hinged at both ends is
(9.207)
The substitution of Eq. (9.207) into Eq. (9.205) leads to the characteristic
equation
(9.208a)
which yields
(9.208b)
where
n
is the nth natural frequency coefficient. Since K
f
0, we see that
the presence of the elastic foundation always increases the natural frequencies
of the beam, and that a tensile axial force ( 0) always increases the natu-
ral frequencies while a compressive axial force ( 0) always decreases
them. For compressive axial forces one must make sure that the buckling lim-
its of the beam are not exceeded. The buckling limits are also a function of the
boundary conditions.
P
ˆ
P
ˆ
n
2
4
1np 2
4
P
ˆ
1np 2
2
K
f
n 1, 2, . . .
1np 2
4
P
ˆ
1np 2
2
K
f
4
0
W1h 2 sin1nph 2
n 1, 2, . . .
P
ˆ
p
o
L
2
EI
and
K
f
k
f
L
4
EI
d
4
W
dh
4
P
ˆ
d
2
W
dh
2
1K
f
4
2W 0
EI
0
4
w
0x
4
p
o
0
2
w
0x
2
k
f
w1x,t 2 rA
0
2
w
0t
2
f 1x,t 2
626 CHAPTER 9 Vibrations of Beams
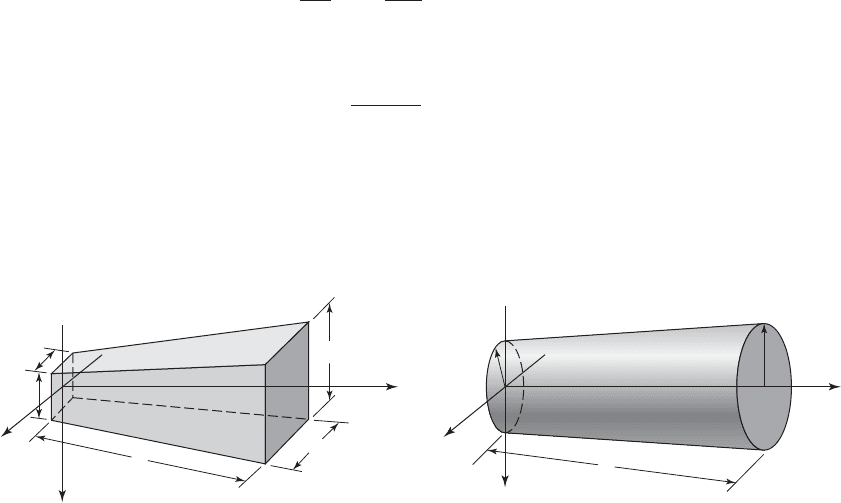
9.3.7 Tapered Beams
33
We shall now remove the assumption that the beam has a constant cross-
section and consider beams whose cross-section varies with the position
along the length of the beam, as shown in Figure 9.32. This permits us to
model such systems as fly fishing rods,
34
baseball bats, and chimneys.
35
We
assume that p k
f
f(x,t) 0 in Eq. (9.40) and that the solution is of the
form given by Eq. (9.58). In addition, we assume that
(9.209)
where A
o
and I
o
are constants, and a(h) and i(h) are nondimensional functions
of h. Then, Eq. (9.40) and Eqs. (9.209) lead to the spatial equation
(9.210)
where we have used the notation of Eqs. (9.67) and introduced the quantity
(9.211)
Consider the double-tapered beam with rectangular cross-section shown
in Figure 9.32a; that is, a beam that tapers in both the xz-plane and the
xy-plane. Let us assume that the taper ratios a h
1
/h
o
1 in the xz-plane and
b b
1
/b
o
1 in the xy-planes are equal, that is, a b, where h
1
, h
o
, b
1
, and
4
0
rA
o
v
2
L
4
EI
o
d
2
dh
2
ci1h2
d
2
W
dh
2
d
4
o
a1h 2W 0
I I
o
i1h 2
A A
o
a1h 2
9.3 Free Oscillations 627
33
For a general treatment of tapered beams see E. B. Magrab, ibid, pp. 153–168.
34
J. A. Hoffmann and M. R. Hooper, “Fly Rod Response,” J. Sound Vibration, Vol. 209, No. 3,
pp. 537–541 (1998).
35
K. Güler, “Free Vibrations and Modes of Chimneys on an Elastic Foundation,” J. Sound Vibra-
tion, Vol. 218, No. 3, pp. 541–547 (1998).
b
1
r
1
h
o
r
o
b
o
h
1
L
L
(a)
(b)
y
y
z
z
x
x
FIGURE 9.32
Geometry of a tapered beam: (a) rectangular cross-section and (b) circular cross-section.
b
o
, are as defined in Figure 9.32a. For this beam, the functions a(h) and i(h)
are, respectively,
(9.212)
and
(9.213)
On substituting Eqs. (9.212) into (9.210), we obtain
(9.214)
To solve Eq. (9.214), we introduce the transformation from the spatial
variable h to another spatial variable w
(9.215)
and note that
(9.216)
After substituting Eq. (9.215) into Eq. (9.214) and making use of Eqs.
(9.216), we arrive at
(9.217)
where
The general solution to Eq. (9.214) is
36
(9.218)
where J
2
(z) and Y
2
(z) are the Bessel functions of the first and second kind, re-
spectively, and I
2
(z) and K
2
(z) are the modified Bessel functions of the first
and second kind, respectively.
A
3
I
2
12l 1w2 A
4
K
2
12l 1w24
W1w 2 w
1
3A
1
J
2
12l 1w2 A
2
Y
2
12l 1w2
l
o
11 a2
d
2
dw
2
cw
4
d
2
W
dw
2
d l
4
w
2
W 0
d
2
dh
2
11 a 2
2
d
2
dw
2
d
dh
11 a 2
d
dw
w a 11 a2h
d
2
dh
2
c3a 11 a 2h 4
4
d
2
W
dh
2
d
4
o
3a 11 a 2h 4
2
W 0
A
o
b
o
h
o
I
o
b
o
h
3
o
12
i1h 2 3a 11 a 2h 4
3
3b 11 b 2h 4 3a 11 a 2h 4
4
a1h 2 3a 11 a 2h 43b 11 b2h4 3a 11 a 2h 4
2
628 CHAPTER 9 Vibrations of Beams
36
E. B. Magrab, ibid., p. 26.

The boundary conditions for a tapered beam is chosen from those given
in Table 9.1, except that we rewrite them in terms of the independent variable
w using Eqs. (9.209), (9.212), and (9.215). We now illustrate these results
with two examples.
EXAMPLE 9.5
Natural frequencies of a tapered cantilever beam
We shall determine the characteristic equation for a tapered cantilever beam
clamped h 1. In terms of the spatial variable w, the boundary conditions at
h 1 correspond to w 1. Thus, the boundary conditions at h 1 are
(a)
At the free end, h 0, which corresponds to w a, we have
(b)
where we have used the first boundary condition of Eqs. (b) to simplify the
second boundary condition.
On substituting Eq. (9.218) into the boundary conditions given by Eqs.
(a) and (b) and setting the determinant of the coefficients A
j
to zero, we obtain
the following equation:
(c)
In arriving at Eq. (c), we used the following relations:
d
dw
3w
n/2
K
n
12l 2w24lw
1n12/2
K
n1
12l 2w2
d
dw
3w
n/2
I
n
12l 2w24 lw
1n12/2
I
n1
12l 2w2
d
dw
3w
n/2
Y
n
12l 2w24lw
1n12/2
Y
n1
12l 2w2
d
dw
3w
n/2
J
n
12l 2w24lw
1n12/2
J
n1
12l 2w2
4
J
5
12l 1a2 Y
5
12l 1a2 I
5
12l 1a2 K
5
12l 1a2
J
4
12l 1a2 Y
4
12l 1a2 I
4
12l 1a2 K
4
12l 1a2
J
2
12l 2 Y
2
12l 2 I
2
12l 2 K
2
12l 2
J
3
12l 2 Y
3
12l 2 I
3
12l 2 K
3
12l 2
4 0
씮 4w
3
d
2
W1a 2
dw
2
w
4
d
3
W1a 2
dw
3
0 씮
d
3
W1a 2
dw
3
0
d
dh
aEI
d
2
W
dh
2
b 0 씮 11 a2
3
EI
o
d
dw
aw
4
d
2
W
dw
2
b 0
d
2
W
dh
2
0 씮 11 a2
2
d
2
W1a 2
dw
2
0 씮
d
2
W1a 2
dw
2
0
dW
dh
`
h1
0 씮 11 a2
dW
dw
`
w1
0 씮
dW11 2
dw
0
W11 2 0
9.3 Free Oscillations 629
