Balakumar Balachandran, Magrab E.B. Vibrations

Подождите немного. Документ загружается.

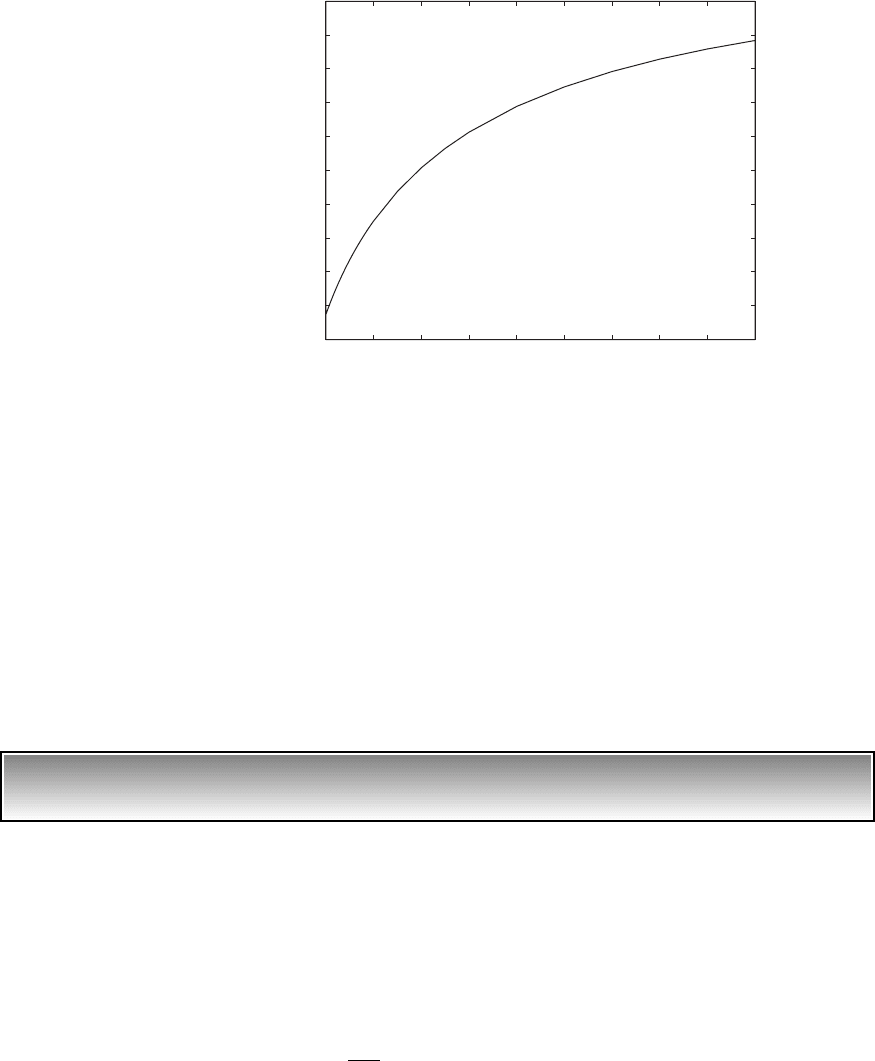
The ﬁrst natural frequency coefﬁcient determined from Eq. (c) is shown

in Figure 9.33 as a function of a, where

and l

is the lowest root of Eq. (c). Upon using Eq. (9.211) and Figure 9.33,

we see that a cantilever beam with a taper of a  0.667 (1/a  1.5) increases

the ﬁrst natural frequency coefﬁcient by 8.8% compared to that for a uniform

cantilever beam, whose ﬁrst natural frequency coefﬁcient is 1.875. (See

Case 4 in Table 9.3.) From Eq. (9.94), we see that this increases the natural

frequency by 18.4%.

EXAMPLE 9.6

Mode shape of a baseball bat

Let us consider a baseball bat-like beam, which shall be modeled as a tapered

beam that is free at each end. We shall determine the mode shape of this beam,

compare it to the mode shape of a uniform beam that is free at each end, and then

based on the results for the tapered beam make some judgments as to where one

should strike the ball. For the conical beam shown in Figure 9.32b, we have that

a  b  r

 1, where r

is the radius of the beam cross-section at h  1 and

is the radius of the beam cross-section at h  0. The taper functions a(h) and

i(h) given by Eqs. (9.212) are still applicable. In this case, Eqs. (9.213) become

(a)A

 pr





 l

11  a2

630 CHAPTER 9 Vibrations of Beams

1 2 3 4 5 6 7 8 9 10

1.8

1.9

2.1

2.2

2.3

2.4

2.5

2.6

2.7

2.8

1/a

Ω

FIGURE 9.33

First natural frequency coefﬁcient

for a double tapered cantilever

beam with a  b.

At the end h  1, which corresponds to w  1 from Eq. (9.215), we have the

boundary conditions

(b)

At the end h  0, which corresponds to w  a, we have the boundary condition

(c)

On substituting Eq. (9.218) into the boundary conditions given by Eqs. (b)

and (c) and setting the determinant of the coefﬁcients A

to zero, we obtain the

following equation

(d)

The evaluation of Eq. (d) for a taper ratio of a  1/2.2  0.4545 leads to

the frequency ratio 

 4.081. This is lower than the value of 

 4.730

for a uniform beam free at each end obtained from Case 5 of Table 9.3. The

corresponding mode shape is shown in Figure 9.34 along with the mode shape

for the uniform beam. In the ﬁgure, the right-hand end of the beam is the fat-

ter end. It is seen that at the fatter end of the tapered beam, as the taper ratio

is increased the node point “moves” toward the end of the beam whereas, at

12l 1a2 Y

12l 1a2 I

12l 1a2 K

12l 1a2

12l 1a2 Y

12l 1a2 I

12l 1a2 K

12l 1a2

12l 2 Y

12l 2 I

12l 2 K

12l 2

12l 2 Y

12l 2 I

12l 2 K

12l 2

4 0

W1a 2

 0

W1a 2

 0

W11 2

 0

W11 2

 0

9.3 Free Oscillations 631

FIGURE 9.34

Comparison of the ﬁrst mode shape

of a tapered beam with circular

cross-section with a  1/2.2 and a

uniform beam. The fatter end of the

tapered beam is at the right end.

Uniform beam

Tapered beam

the thinner end, it moves toward the interior of the beam. In order for the beam

to act as a rigid member, at least as far as exciting the ﬁrst mode shape, one

should strike the ball at the beam’s (bat’s) node point. That is, if the bat were

to strike the ball close to a node point of the ﬁrst mode, then the ﬁrst mode of

the bat will not be excited and there will be no energy transferred due to the

vibrations of the ﬁrst mode of the bat. Usually, the so-called sweet spot of a

baseball bat is at the node of the ﬁrst mode located near the fat end of the bat.

This tends to impart the maximum force to the ball, and frequently, the result

is that we hear it as the “crack” of the bat.

9.4 FORCED OSCILLATIONS

In Section 9.3, we studied the responses of different beam systems during free

oscillations. In this section, we shall study the response of beams to externally

applied dynamic transverse loading as shown in Figure 9.35. To solve for the

response, we shall use the normal mode approach and the technique of separa-

tion of variables. To simplify matters, we shall assume that the boundary con-

ditions are independent of time; that is, boundary conditions 9 and 10 in Table

9.1 will not be considered. We assume that the damping force is proportional to

the transverse velocity of the beam; that is, from Eq. (9.41c) we have

(9.219a)

where c has the units of Ns/m

Expressing the external loading f(x,t) as

(9.219b)

the equation of motion for the damped vibrations of the beam is obtained from

Eqs. (9.40) and (9.41c). Thus,

(9.220)

Governing Equations in Terms of Nondimensional Quantities

Employing the notation of Eqs. (9.67), Eq. (9.220) is rewritten as

(9.221)

where the nondimensional spatial variable h  x/L, the nondimensional time

variable t  t/t

(9.222)2z 

g1h,t 2

1h,t 2

 2z



 g1h,t 2

 c

 rA

 f

1x,t 2

f 1x,t2 f

1t 2 f

1x,t 2

1t 2c

632 CHAPTER 9 Vibrations of Beams

R. K. Adair, “The crack-of-the-bat: the acoustics of a bat hitting the ball,” Paper No. 5pAA1,

141st Acoustical Society of America Meeting, Chicago, IL, June 2001.

f(x, t)

x  0 x  L

FIGURE 9.35

Forced oscillations of a beam.

and z is the nondimensional damping factor, t

has the units of time, and

g(h,t) has the same units as w(h,t).

For the system shown in Figure 9.35, and making use of Eqs. (9.47), the

boundary conditions at h  0 are

(9.223)

and the boundary conditions at h  1 are

(9.224)

where B

and K

, j  1,2, are deﬁned in Eq. (9.67). We recall that the form of

the boundary conditions given by Eqs. (9.223) and (9.224) have been chosen

so that we can examine a wide range of boundary conditions by independ-

ently varying the values of B

and K

, j  1, 2, from zero to inﬁnity.

Solution for Response

To determine the response of the forced system described by Eqs. (9.221),

(9.223), and (9.224) and the speciﬁed initial conditions w  w(h,0) and (h,0),

we make use of the mode shapes obtained from the free oscillation problem. For

the boundary conditions given by Eqs. (9.223) and (9.224), it is known from the

material of Section 9.3 that the mode shapes W

(h) are orthogonal functions, the

general form of which is given by Eqs. (9.89) or (9.91). In the present case, W

(h)

is a solution of the undamped system given by Eq. (9.70); that is,

(9.225)

with the boundary conditions at h  0 being

(9.226)

and those at h  1 being

(9.227)

The solution for the forced response of the system is assumed to be of

the form

(9.228)w1h,t 2

n 1

1t 2W

1h 2

W‡

11 2 K

11 2

W–

11 2B

W¿

11 2

W‡

10 2K

10 2

W–

10 2 B

W¿

10 2



 0

w11,t 2

 K

w11,t 2

B

0w11,t2

w10,t 2

K

w10,t 2

 B

0w10,t2

9.4 Forced Oscillations 633

where W

(h) are determined from the spatial eigenvalue problem associated

with the undamped free oscillations of the system; that is, Eqs. (9.225) to

(9.227) and the summation are taken over the inﬁnite number of modes. Since

(h) is a nondimensional quantity, 

(t) has the same units as w(h,t). The

time-dependent functions 

(t), also referred to as modal amplitudes, are un-

known quantities that remain to be determined.

We substitute Eq. (9.228) into Eq. (9.221) to obtain

(9.229)

where it is noted that due to the choice of the nondimensional variables each

term in Eq. (9.229) has displacement units. Upon substituting Eq. (9.225) into

Eq. (9.229) for the ﬁrst term on the left-hand side, we obtain

(9.230)

We now multiply Eq. (9.230) by W

(h), integrate over the interval 0  h  1,

and use the orthogonality property expressed by Eq. (9.77) with M



 0 to obtain

(9.231)

where

(9.232)

and G

(t) has displacement units and N

is a nondimensional quantity.

Equation (9.231), which governs the variation of the modal amplitude



(t), is similar to the equation governing a single degree-of-freedom system

discussed in Chapters 3 to 6. Therefore, the problem of determining the

forced response of the system has been reduced to the problem of solving for

the modal amplitudes 

(t), each of whose governing equation is similar to

the equation governing a single degree-of-freedom system. The orthogonality

of the mode shapes is crucial to realizing this step.

Cases When a Mode Is Not Excited

On examining Eq. (9.231), it is clear that if G

(t)  0, then that particular

mode corresponding to 

does not get excited by the forcing. This is possi-

ble in the following two cases. In the ﬁrst case, we assume that the forcing is

acting at a point such that





1h 2dh

1t 2



1h 2g1h,t2dh

 2z

d°



 G

1t 2

n  1,2, . . .

c

 2z

d°



 g1h,t 2

n1

 2zW

d°

 W

d g1h,t2

634 CHAPTER 9 Vibrations of Beams

(9.233a)

Then, we obtain from Eqs. (9.232) that

(9.233b)

If h

is a node point, then W

)  0 and G

(t)  0. To show this, we con-

sider a beam simply supported at each end. The mode shape is given by

Eq. (2b) of Table 9.2 and Case 2 of Table 9.3, and from Eq. (9.233b), G

(t)

becomes

which is zero at h

 1/n, n  2, 3, . . . . Conversely, G

(t) is also zero, for

example, when h

 0.5 and n  2, 4, . . . .

In the second case, we assume that the spatial distribution of the forcing

is such that

(9.234a)

Equation (9.234a) is satisﬁed when the forcing function is orthogonal to the

mode shape; that is, let

(9.234b)

where W

(h) is one of the orthogonal functions. In this case, we obtain from

Eqs. (9.232) that

(9.234c)

and, therefore, all the modal amplitudes are zero except for n  m.

Solution for Response (continued)

The solution to Eq. (9.231) is obtained by using the Laplace transform, and

we follow the procedure used to obtain Eq. (D.11a) of Appendix D. In order

to make use of Eq. (D.11a), we rewrite Eq. (9.231) as

(9.235)

where

(9.236)z





 2z



d°



 G

1t 2

n  1,2, . . .

1t 2



1h 2F1t2W

1h 2dh  F1t 2d

g1h,t 2 F1t 2W

1h 2



1h 2g1h,t2dh  0

1t 2

F1t 2

sin1nph

1t 2



1h 2F1t2d1h  h

2dh 

F1t 2

g1h,t 2 F1t 2d1h  h

9.4 Forced Oscillations 635

The Laplace transform of Eq. (9.235) is given by Eq. (D.2) of Appendix D if

we identify 

(t) with x(t), z with z

, v

with 

, and we set F(s)/m  (s).

Thus, if the Laplace transform of 

(t) is (s), then in the Laplace domain

we have

(9.237)

where the overdot indicates the derivative with respect to t and the modal ini-

tial conditions are given by 

(0) and (0). Making use of Eq. (9.228),

these initial conditions are determined from

(9.238)

where

If we multiply each of Eqs. (9.238) by W

(h), integrate over the interval

0  h  1, and make use of Eq. (9.77) with M

 J

 0, we obtain the modal

initial conditions

(9.239)

Assuming that 0  z

 1, the inverse transform of Eq. (9.237) is ob-

tained from Eq. (D.11a) as

(9.240)

where 

(t) is the nth modal amplitude and

(9.241)

is the damped natural frequency coefﬁcient associated with the nth mode.





21  z







zt¿

sin 1

t¿ 2G

1t  t¿ 2dt¿

1t 2 °102e

zt

cos1

t2

10 2 z°10 2



zt

sin 1

10 2



1h 2w

1h,0 2dh

n  1,2, . . .

10 2



1h 2w1h,02dh

n  1,2, . . .

1h,0 2

dw1h,0 2

1h,0 2

n1

10 2W

1h 2

w1h,0 2

n1

10 2W

1h 2

1s 2

1s 2 1s  2z



2°

10 2 °

10 2

 2z



s 

636 CHAPTER 9 Vibrations of Beams

Forced Response in the Damped Case

Upon using Eqs. (9.228), (9.232), and (9.240), the displacement of the beam is

(9.242a)

The ﬁrst term inside the brackets is the forced response in the nth mode and

the second and third terms are the responses of the nth mode to the initial con-

ditions. Making use of Eqs. (9.67) and (9.222), we can rewrite Eq. (9.242a) in

terms of the dimensional quantities as

(9.242b)

where

and

Forced Response in the Undamped Case

When the damping is absent, Eq. (9.242a) simpliﬁes to

(9.243a) cos

1



1h 2w1h,02dh 

sin1





1h 2w

1h,0 2dh d

w1h,t 2

n1

1h 2





g1h,t  t¿ 2W

1h 2sin 1

t¿ 2dh ddt¿

z¿  z/t

 v

21  z



z¿t

sin 1v



1x/L 2e

0w1x,02

 z¿w1x,02fdxd

 e

z¿t

cos 1v



1x/L 2w1x,02dx

w1x,t 2

1x/L 2



z¿t¿

sin 1v

t¿ 2f

1x,t  t¿ 2W

1x/L 2dx fdt¿



zt

sin 1





1h 25w

1h,0 2 zw1h,026dh d

 e

zt

cos 1



1h 2w1h,02dh

w1h,t 2

n1

1h 2





zt¿

sin1

t¿ 2g1h,t  t¿ 2W

1h 2dh fdt¿

9.4 Forced Oscillations 637

In terms of the dimensional quantities, we rewrite Eq. (9.219b) as

(9.243b)

Equation (9.242a) describes the forced response of the system governed

by Eqs. (9.221) to (9.224) and the speciﬁed initial conditions, and they have

been expressed as a sum of the responses of the individual modes. In practice,

the inﬁnite sum shown in Eq. (9.242a) is replaced by a ﬁnite number of terms,

with this number depending on the frequency content of the excitation.

EXAMPLE 9.7

Impulse response of a cantilever beam

We shall determine the displacement response of an undamped cantilever

beam that is initially at rest and subjected to an impulse force at h  j  x

/L.

In this case, c  0 in Eq. (9.220) and z  0 in Eq. (9.221). Since the beam

is initially at rest, the initial conditions are

(a)

and the forcing is expressed as

(b)

Upon substituting Eqs. (a) and (b) into Eq. (9.243a), and carrying out the in-

tegration, we ﬁnd that

(c)

Upon using Eqs. (9.243b), we rewrite Eq. (c) in terms of the dimensional

quantities as

(d)

where f

is the magnitude of the impulse at x  x

in N s.

The values of 

are given in Case 4 of Table 9.3. The modes W

(h) are

given by Eq. (4b) of Table 9.2. The beam displacement given by Eq. (c) is plot-

ted in Figure 9.36 for impulses applied at h

 0.4 and h

 1. In each case,

the displacement pattern is shown at different instances of the nondimen-

sional time t. Each beam displacement was obtained after truncating the sum-

mation to 11 modes in Eq. (c).

w1x,t 2

n1

1x/L 2W

/L 2

sin 1v

w1h,t 2 g

n1

1h 2W

1j 2



sin 1

g1h,t 2 g

d1h  j 2d1t2

w1h,0 2 w

1h,0 2 0



cos 1v



1x/L 2w1x,02dx 

sin 1v



1x/L 2

0w1x,02

dx d

w1x,t 2

n1

1x/L 2



sin 1v

t¿ 2f

1x,t  t¿ 2W

1x/L 2dx fdt¿

638 CHAPTER 9 Vibrations of Beams

(a)

(b)

  0.1

  0.4

  0.7

  1

  1.3

  1.6

  1.9

  2.2

  2.5

  2.8

  3.1

  3.4

  0.1

  0.4

  0.7

  1

  1.3

  1.6

  1.9

  2.2

  2.5

  2.8

  3.1

  3.4

FIGURE 9.36

Normalized response of a cantilever beam subjected to an impulse force:

(a) h

 0.4 and (b) h

 1.