Baggott J. The Quantum Story: A History in 40 Moments

Подождите немного. Документ загружается.

the quantum story

ﬁ nish it in a hurry, and to do that I have taken off a couple of days from

the laboratory (this is also a secret).

The model was still nevertheless rife with contradictions. He summa-

rized his work in a manuscript he submitted to Rutherford on 6 July,

but which was never published. He left Manchester and returned to

Copenhagen a couple of weeks later, carrying the problems back with

him in his briefcase. On 1 August he and Margrethe were married. They

honeymooned in England, Bohr returning to the Cambridge and Man-

chester laboratories for brief visits before setting off for a holiday in

Scotland and then back to Copenhagen, where an academic position

now awaited him.

Bohr continued to work on the problem of atomic structure through

the rest of 1912 and into early 1913. For his hypothesis concerning the sta-

ble orbits to have any value, he needed to use it to explain the results of

recent experiments or predict the results of experiments yet to be done.

His next breakthrough came in February 1913, when he was given a clue

that would unlock the entire mystery. Hans Hansen, a young professor

of physics who had done some experimental work on atomic spectros-

copy at the University of Göttingen in Germany, drew Bohr’s attention

to something called the Balmer formula.

Spectroscopy is the study of the absorption and emission of electromag-

netic radiation by atoms and molecules. The simplest atoms exhibit the

simplest spectra and the hydrogen atom, consisting of a nucleus and just

one electron, has the simplest spectrum of all. Whilst it might have been

anticipated from classical physics that atoms such as hydrogen should

absorb and emit energy continuously, favouring no particular radiation fre-

quencies, the opposite is actually found. The hydrogen emission spectrum

is a ‘line’ spectrum of discrete, narrowly deﬁ ned frequencies.

In 1885, the Swiss mathematician Johann Jakob Balmer had studied the

measurements of one series of hydrogen emission lines and found them

to follow a relatively simple pattern. He found that the frequencies of the

lines are proportional to the differences between the inverse squares of

pairs of integer numbers. In other words, the frequencies depend on the

numbers m and n where, for the hydrogen series that Balmer had investi-

gated, m = 2 and n takes the values 3, 4, 5, and so on.

a little bit of reality

Balmer’s formula was generalized in 1888 by Swedish physicist

Johannes Rydberg. He found that other spectral series follow a similar

relation, with the value of m taking different integer values. In themselves

the Balmer and Rydberg formulas were purely empirical and their origin

in terms of the underlying physics of the atom was quite obscure. Bohr,

however, immediately understood where the integer numbers had come

from.

He realized that an electron moving from an outer, high-energy orbit

to a lower-energy inner orbit causes the release of energy as emitted

radiation. If, as he had hypothesized, the orbits are ﬁ xed, with energies

that depend on integer numbers that can be counted outwards from the

nucleus in a linear sequence, then the energy differences between the

orbits are also therefore ﬁ xed.

For example, in the case where an electron circling the nucleus in

orbits characterized by the integer numbers n = 3, 4, 5, . . . drops down

into a lower-energy orbit characterized by m = 2 the result is the series

of emission lines studied by Balmer, which had become known as the

Balmer series. Putting m = 3 and n = 4, 5, 6, . . . gives another series that

had been observed in 1908 by German physicist Friedrich Paschen. Bohr

predicted the existence of a further series in the ultraviolet with m = 1,

and series in the infrared characterized by m = 4 and 5.

Bohr was further able to show that the constant of proportionality that

appeared in Rydberg’s formula (known as the Rydberg constant) can be

calculated directly by combining a number of fundamental physical con-

stants, including Planck’s constant, the electron charge, and the electron

mass. The Rydberg constant was well known at the time from spectro-

scopic measurements. Bohr’s calculation was within six per cent of the

experimental value, a margin well within the experimental uncertainty

of the values he had used for the fundamental constants.

A further series of emission lines named for American astronomer

and physicist Edward Charles Pickering was thought by experimental-

ists also to belong to the hydrogen atom. However, at the time, the Pick-

ering series was characterized by half-integer numbers which are not

admissible in Bohr’s theory. Instead, Bohr proposed that the formula

be rewritten in terms of integer numbers, suggesting that the Pickering

series belongs not to hydrogen atoms but to ionized helium atoms. An

the quantum story

awkward mismatch was later resolved by Bohr himself. The correction

gave a Rydberg constant for ionized helium some 4.00163 times greater

than that for hydrogen. The experimentalists had found this ratio to be

4.0016. This kind of agreement between theory and experiment was

simply unprecedented.

Bohr’s idea of stable electron orbits had a further consequence. The

electrons had to possess a ﬁ xed angular momentum—a ﬁ xed momen-

tum associated with their ‘rotation’ around the central nucleus—in units

of h divided by 2p. Transitions between the orbits had to occur in instan-

taneous ‘jumps’, because if the electron were to move gradually from one

orbit to another, it would again be expected to radiate energy continu-

ously during the process. Transitions between inherently non-classical

stable orbits must themselves involve non-classical discontinuous jumps.

Bohr wrote that:

. . . the dynamical equilibrium of the systems in the [stable orbits] can be

discussed by help of the ordinary mechanics, while the passing of the sys-

tems between the different [stable orbits] cannot be treated on that basis.

The integer numbers that characterize the electron orbits would come

to be known as quantum numbers, and the transitions between different

orbits would be called quantum jumps.

Bohr wrote to Rutherford on 6 March 1913, enclosing with his letter a

manuscript with the title: ‘On the Constitution of Atoms and Molecules’.

In his reply Rutherford reacted favourably but raised some difﬁ cult ques-

tions. He was particularly puzzled by the fact that, in Bohr’s model, an

electron in a high-energy orbit would somehow need to ‘know’ before-

hand the energy of the ﬁ nal, destination, orbit in order to emit radia-

tion of just the right frequency. Rutherford was already ringing alarm

bells about the implications of the new quantum theory for our under-

standing of cause-and-effect, bells that would continue to peal loudly for

another century.

He also warned that Bohr’s manuscript was rather long: ‘I do not know if

you appreciate the fact that long papers have a way of frightening readers,’

he wrote. Bohr was nonplussed. The day before he received Rutherford’s

letter he had sent a revised draft of his manuscript. It was even longer.

a little bit of reality

Bohr resolved to go at once to Manchester and discuss the paper directly

with Rutherford. He wrote back on 26 March and declared his intention

to visit Rutherford in the ﬁ rst days of the following week. Rutherford was

patient. After discussions through several long evenings, during which

he declared he had never thought Bohr should prove to be so obstinate,

he agreed to leave all the detail in the ﬁ nal paper and communicate it to

the journal Philosophical Magazine on Bohr’s behalf.

The paper was published in July 1913, and was followed by two further

papers published in the same journal in September and November that

year.

Bohr’s model of atomic structure was a triumph. But, much like Planck’s

achievement in 1900, it was also rather mysterious. There were many

unanswered questions. The most pressing of these concerned the quan-

tum numbers. What did they mean? From where, exactly, had they

come?

Experiment forced the pace on the new quantum theory of the atom. It turned out that

the spectrum of the hydrogen atom was not quite so simple, after all. Some of the lines in

the spectrum had already been found some years before actually to be two, closely spaced

lines. Furthermore, lines in the spectrum were found to be split in low-intensity elec-

tric and magnetic ﬁ elds. In addition to Bohr’s quantum number n, German physicist

Arnold Sommerfeld introduced two additional quantum numbers, k and m, to explain

the experimental results. These new quantum numbers were thought to be related in some

way to the quantization of the geometry of the stable electron orbits.

As the various lines in the spectrum were identiﬁ ed with different quantum jumps

between different orbits, it was soon discovered that not all the possible jumps were

appearing. Some lines were missing. For some reason certain jumps were forbidden. An

elaborate scheme of ‘selection rules’ was established by Bohr and Sommerfeld to account

for those jumps that were allowed and those that were forbidden.

In the meantime, evidence for Einstein’s light-quantum hypothesis was also accu-

mulating. Einstein had used his hypothesis to make predictions about the photoelectric

effect, predictions that were duly borne out in experiments by American physicist Rob-

ert Millikan in 1915.

The status of light ‘particles’ was further enhanced when, in 1923,

la Comédie Française

Paris, September 1923

Einstein was awarded the 1921 Nobel Prize for physics for his work on the photoelectric

effect (not relativity). Bohr was awarded the 1922 Nobel Prize for his work on atomic structure.

Planck had been awarded the Prize in 1918 for his discovery of the quantum.

la comédie française

American physicist Arthur Compton and Dutch theorist Pieter Debye showed that light

quanta could be ‘bounced’ off electrons, with a consequent (and predictable) change in

their frequencies. These experiments appeared to demonstrate that light consists of parti-

cles with directed momenta, like small projectiles.

Despite this evidence, many physicists, including Planck and Bohr, dismissed the

light-quantum. They preferred to think of quantization as having its origin in atomic

structure, retaining Maxwell’s classical wave description for electromagnetic radiation.

Whatever theory was going to replace classical physics had to confront the difﬁ cult task

of somehow reconciling the wave-like and particle-like aspects of light in a single theory.

And, somehow, this theory also had to account for the inner structure of the atom. It had

to account for the stable electron orbits characterized by their quantum numbers.

An important clue would come from Einstein’s special theory of relativity.

Einstein had introduced his special theory in the fourth paper he pub-

lished in 1905. He had struggled, and failed, to ﬁ nd a way to reconcile one

of the most disturbing observations in late nineteenth-century physics

with the body of accepted classical theory.

When in 1887 Michelsen and Morley could ﬁ nd no evidence for

relative motion between the earth and the hypothetical, all-pervading

ether they concluded that the speed of light is constant and independent

of the motion of the light source. This was one of the most important

‘negative’ experiments ever performed, and led to the award of the 1907

Nobel Prize for physics to Michelsen.

The absence of an ether and an apparently universal speed of light

could not be accommodated in any kind of Newtonian conception of

absolute space and time. As he had done some months earlier for the

light-quantum, now Einstein decided to build a new theory out of the

bare minimum of assumptions in which the observations made by

Michelson and Morley would result. He found that he needed only two.

He assumed that the laws of physics should be identical for all observ-

ers. In particular, they should not depend in any way on how an observer

is moving in uniform motion, relative to an observed object. In practical

terms, this means that the laws of physics should appear to be identical

in any so-called inertial frame of reference, and so all such frames of ref-

erence are equivalent. An observer stationary in one frame of reference

(standing on the ground, say) should be able to draw the same conclusions

the quantum story

from some set of physical measurements as another observer moving

uniformly relative to the ﬁ rst, or stationary in his own moving frame of

reference, such as a moving train or a spaceship.

Einstein also assumed that the speed of light should be regarded as a

fundamental, universal constant, representing an ultimate speed which

cannot be exceeded.

From these assumptions there ﬂ owed a number of bizarre consequences.

Out went any idea of an absolute frame of reference (and hence the idea of

a stationary ether), together with absolute space, time, and simultaneity.

In came all sorts of strange effects predicted for moving objects and clocks

within what came to be recognized as a four- dimensional spacetime. The

theory was ‘special’ only insofar as it treated the special case of observers

moving in constant uniform motion in a straight line.

As Einstein explained it to his Olympia Academy friend Maurice

Solovine:

All movements of bodies were supposed to be relative to the light-carrying

ether, which was the incarnation of absolute rest. But after efforts to dis-

cover the privileged state of movement of this hypothetical ether through

experiments had failed, it seemed that the problem should be restated.

That is what the theory of relativity did. It assumed that there are no privi-

leged physical states of movement and asked what consequences can be

drawn from this.

There was a further, fundamentally important consequence of the principle

of relativity, which Einstein had explored in a short, ﬁ fth paper published in

1905. Suppose a body emits light of total energy E equally in two, opposite

directions. When seen from the perspective of an observer in an inertial

frame of reference moving uniformly with respect to the body, there is a

perceived difference in the amount of energy lost by the body, such that:

. . . its mass decreases by [E/c

]. Here it is obviously inessential that the energy

taken from the body turns into radiant energy, so we are led to the more gen-

eral conclusion: The mass of a body is a measure of its energy-content . . .

The theory demanded that energy and mass be recognized as equivalent

and interchangeable, through the approximate relation E = mc

la comédie française

Pronounced ‘de Broy’.

This relation suggests that energy can be considered equivalent to mass,

and that all mass represents energy. Einstein’s earlier light-quantum

hypothesis makes the connection between the energy of a light-quantum

and its frequency. Now there were two simple, yet fundamental equa-

tions connecting energy to mass and energy to frequency. This seems to

beg an obvious question. Could these equations be combined?

French physicist Prince Louis de Broglie certainly thought so.

Thirty-one year old de Broglie

was the younger son of Victor, ﬁ fth duc

de Broglie. He had originally intended a career in the humanities, and had

studied medieval history and law at the Sorbonne, receiving a degree in

1910. But he gained a passion for physics through the inﬂ uence of his older

brother Maurice and his experiences during World War I serving in the

French Army, in ﬁ eld radio communications, stationed at the Eiffel Tower.

After the war, de Broglie joined a private physics laboratory headed by

his brother which specialized in the study of X-rays. It was whilst he was

working at this laboratory in 1923 that he thought to combine the two

most iconic equations of special relativity and quantum theory:

The notion of a quantum makes little sense, seemingly, if energy is to be

continuously distributed through space; but, we shall see that this is not

so. One may imagine that, by cause of a meta law of Nature, to each por-

tion of energy with a proper mass [m], one may associate a periodic phe-

nomenon of frequency [n], such that one ﬁ nds . . . [hn = mc

This seemed to imply that a light-quantum with frequency n would pos-

sess a mass, and hence a momentum, calculable as mass times velocity.

Such directed momentum had been revealed in Compton’s experiments,

so this appeared to make sense.

But it was de Broglie’s next step that was breathtaking. He later wrote:

After long reﬂ ection in solitude and meditation, I suddenly had the idea, dur-

ing the year 1923, that the discovery made by Einstein in 1905 should be gen-

eralized by extending it to all material particles and notably to electrons.

If electromagnetic waves, characterized by a frequency n, possessed

associated particle-like properties such as momentum then, de Broglie

the quantum story

reasoned, perhaps particles such as electrons, characterized by a mass m,

might possess associated wave-like properties. He went on:

An electron is for us the archetype of [an] isolated parcel of energy, which

we believe, perhaps incorrectly, to know well; but, by received wisdom, the

energy of an electron is spread over all space with a strong concentration

in a very small region, but otherwise whose properties are very poorly

known. That which makes an electron an atom of energy is not its small

volume that it occupies in space, I repeat: it occupies all space, but the fact

that it is undividable, that it constitutes a unit.

De Broglie was suggesting that the electron could be thought of as a wave. A

beam of electrons could be diffracted, just like a beam of light. The connec-

tion could be reduced to a simple equation, l = h/p, the wavelength of the

wave is equal to Planck’s constant divided by the momentum, p (mass times

velocity), of the particle. That this wave nature of particles is not apparent

in everyday macroscopic objects is due to the very small size of Planck’s

constant h.

The dual wave–particle nature of matter is apparent only in the

microscopic world of fundamental particles, atoms, and molecules.

Whatever they were, these ‘matter waves’ could not be considered to be

in any way equivalent to more familiar wave phenomena, such as sound

waves or ripples on the surface of a pond. De Broglie was able to show that

the velocity of such matter waves would be greater than the speed of light—

forbidden in Einstein’s special theory of relativity—and could not therefore

be waves carrying energy. He therefore concluded that the matter wave:

‘represents a spatial distribution of phase, that is to say, it is a “phase wave”.’

The concept of phase was therefore critical to de Broglie’s work right

from the beginning. We can think of phase in terms of a simple sinusoi-

dal oscillation, with ‘peaks’ and ‘troughs’ in the height or amplitude of

the wave. A series of waves in which the peaks and troughs coincide in

space and in time are said to be ‘in phase’.

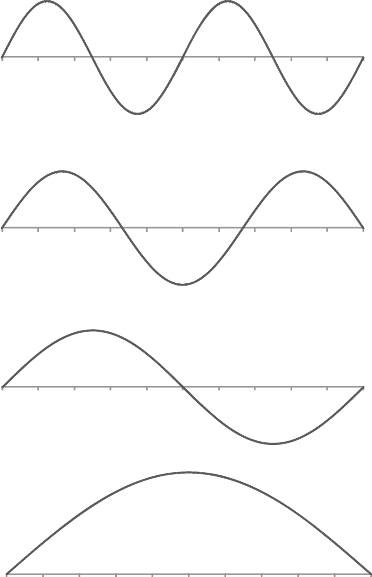
De Broglie’s interest in chamber music now led him to a major break-

through. Musical notes produced by string or wind instruments are

the result of so-called standing waves, vibrational patterns which ‘ﬁ t’

If Planck’s constant were very much larger, the macroscopic world would be an even more

peculiar place than it is.

la comédie française

within the stopped length of the string or the length of the pipe. A vari-

ety of standing wave patterns is possible provided the patterns meet the

requirement that they ﬁ t between the string’s secured ends or the ends

of the pipe. This means that they must have zero amplitude at each end.

This is possible only for vibrational patterns which contain an integral

number of half-wavelengths.

(d)

(c)

(b)

(a)

n=4

n=1

n=2

n=3

fig 3 De Broglie made a connection between the physics of musical notes and

quantum numbers. Musical notes generated by string or wind instruments are

derived from standing wave patterns. These wave patterns must have zero amplitude

at each end of the string or pipe, and so the only possible patterns contain an integral

number of half-wavelengths. In this ﬁ gure, pattern (a) has no nodes (points where

the wave passes through zero), ( b) has one node, (c) has two and (d) has three. If we

deﬁ ne the quantum number n as the number of nodes +1 (or the number of half-

wavelengths) then these patterns correspond to n = 1, 2, 3 and 4.