Baggott J. The Quantum Story: A History in 40 Moments

Подождите немного. Документ загружается.

the quantum story

Theoreticians had simpliﬁ ed the problem by invoking the idea of a

‘black body’, a hypothetical, completely non-reﬂ ecting (i.e. totally black)

object that absorbs and emits light radiation without favouring any par-

ticular range of frequencies. The intensity of radiation emitted by a black

body is directly related to the amount of energy in the body when it is in

thermal equilibrium with its surroundings.

The theoreticians further realized that they could probe the properties of

a black body by studying the radiation trapped inside a cavity consisting of

perfectly absorbing walls, punctured with a small pinhole through which

radiation can enter and leave. Early examples of such cavities included

rather expensive closed cylinders made from porcelain and platinum.

In the winter of 1859–60, the German physicist Gustav Kirchhoff had

demonstrated that the ratio of emitted to absorbed energy depends only

on the frequency of the radiation and the temperature inside the cavity.

It does not depend in any way on the shape of the cavity, the shape of its

walls, or the nature of the material from which the cavity is made. This

implied that something quite fundamental concerning the physics of the

radiation itself was being observed, and Kirchhoff challenged the scien-

tiﬁ c community to discover the origin of this behaviour.

Much progress had been made. Experimental studies of infrared

(or heat) radiation emitted from a radiation cavity had led physicist

Wilhelm Wien in 1896 to devise a relatively simple mathematical relation-

ship between the radiation frequency and cavity temperature. Wien’s

law seemed to be quite acceptable, and was supported by further experi-

ments carried out by Friedrich Paschen at the Technical Academy in

Hanover in 1897. But new experimental results reported in 1900 by Otto

Lummer and Ernst Pringsheim at the Reich Physical-Technical Institute

in Berlin showed that Wien’s law failed at lower frequencies. Wien’s law

was clearly not the answer.

Planck had succeeded Kirchhoff at the University of Berlin in 1889,

rising to full professor in 1892. He was a most unlikely scientiﬁ c revo-

lutionary. Descended from a line of pastors and professors of theology

The study of cavity radiation was not just about establishing theoretical principles, how-

ever. It was also of interest to the German Bureau of Standards as a reference for rating electric

lamps.

the most strenuous work of my life

and jurisprudence, at school Planck was diligent and personable but not

especially gifted. Physics was a subject for which Planck himself felt he

had no particular talent, but he had risen through the academic ranks

and established a solid international reputation. Now in his early for-

ties, he worked at a slow, steady, and conservative pace. He preferred the

stability and predictability of a science which reﬂ ected the character of the

bourgeois German society of which he was a part. By his own subse-

quent admission he was ‘peacefully inclined’, and rejected ‘all doubtful

adventures’.

During a visit to Planck’s villa in the Berlin suburb of the Grünewald

on 7 October 1900, experimental physicist Heinrich Rubens had told him

about some new experimental results he had obtained with his associ-

ate Ferdinand Kurlbaum. They had studied cavity radiation at even lower

frequencies. Ruben’s description of the behaviour of the radiation at these

frequencies set Planck thinking. After Rubens had left, Planck continued

to work alone in his study. He adapted Wien’s earlier law and arrived,

largely through some inspired guesswork, at an expression which ﬁ t all

the available experimental data.

Planck had discovered his radiation law.

The law required two fundamental constants, one relating to temperature

and a second relating to radiation frequency. This second constant would

eventually gain the label h and become known as Planck’s constant. When

combined with the speed of light and Newton’s gravitational constant, the

two constants in Planck’s radiation law promised a fundamental underpin-

ning for all physical quantities. Planck wrote that the constants offered:

‘the possibility of establishing units of length, mass, time and temperature

which are independent of speciﬁ c bodies or materials and which necessarily

maintain their meaning for all time and for all civilizations, even those

which are extraterrestrial and nonhuman, constants which therefore can

be called “fundamental physical units of measurement”.’

He sent Rubens a postcard on which he had written details of the new

radiation law, and he presented a crude derivation of the law at a meet-

ing of the German Physical Society on 19 October. He declared: ‘I there-

fore feel justiﬁ ed in directing attention to this new formula, which, from

the standpoint of electromagnetic radiation theory, I take to be the sim-

plest excepting Wien’s.’ The next day, Rubens advised Planck that he had

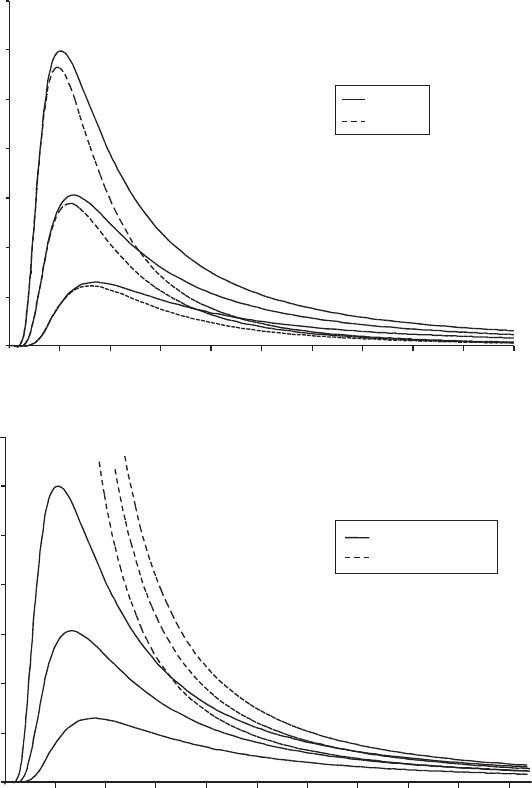
the quantum story

100 200 300 400 500 600 700 800 900 1000

T = 5000 K

Spectral Density

Wavelength/nanometres

T = 4000 K

= 3000 K

Planck

Wien

(a)

T = 5000 K

Spectral Density

Wavelength/nanometres

T = 4000 K

T = 3000 K

Planck

Rayleigh-Jeans

(b)

fig 2 a) Comparison of the predictions of Planck’s radiation law and Wien’s law for

three different temperatures. Wien’s law accurately reproduces the behaviour of black-

body radiation at very high frequencies (short wavelengths) but fails at lower frequen-

cies ( longer wavelengths). The discrepancy is most noticeable at higher temperatures.

b) Planck’s radiation law compared to the Rayleigh-Jeans law for the same three temper-

atures. The Rayleigh-Jeans law approaches the behaviour of black-body radiation at very

low frequencies (very long wavelengths) but gives catastrophic results in the ultraviolet.

the most strenuous work of my life

compared the experimental results with the new law and found ‘com-

pletely satisfactory agreement in all cases’.

It seemed that Planck’s radiation law was the answer, at least as far as

experiment was concerned. Planck now turned his attention to ﬁ nding

a proper theoretical basis for the law, a task which was to lead to ‘some

weeks of the most strenuous work of my life.’

Planck set out the problem in terms of the interaction between the elec-

tromagnetic ﬁ eld and a set of vibrating ‘oscillators’ in the cavity material.

The primary purpose of these oscillators was to ensure that the energy

was properly equilibrated among the possible radiation frequencies

through a continual, dynamic process of absorption and emission.

Being

an expert in entropy and the second law, he began by using the radiation

law to derive an expression for the entropy of an individual oscillator in

terms of its internal energy and its frequency of oscillation, which would

give rise to the same frequency of radiation inside the cavity. This gave

him an expression for the oscillator entropy known to be consistent with

experiment. His challenge now was to derive a similar expression from

‘ﬁ rst principles’, compare the two, and draw appropriate conclusions.

It was this task that proved to be ‘strenuous’. Planck may have tried

several different approaches, but he found that he would always be com-

pelled to return to an expression strongly reminiscent of the statistical

methods of his rival Boltzmann. The mathematics was leading him in a

direction he had not wanted to go.

Boltzmann’s approach to calculating the entropy of a gas was to

assume that its total available energy could be thought of as being organ-

ized into a series of ‘buckets’. The lowest energy bucket was assigned an

energy e, the next an energy 2e, the next 3e, and so on. The gas mol-

ecules would then be distributed among the buckets and the number of

different possible permutations of molecules in the buckets calculated.

In this analysis the energy itself remains continuously variable. All that

Planck originally referred to these as ‘resonators’, but by 1909 he had accepted that the

special properties of resonators were not required. Today we would identify these oscillators as

highly excited electrons within the atoms of the cavity material ( but recall that the very exist-

ence of electrons had been conﬁ rmed only three years earlier, in 1897).

the quantum story

Boltzmann had done was parcel it up so that he could count the number

of molecules in the energy range zero to e, the range e to 2e, and so on, and

thus calculate the number of different possible permutations.

For example, consider a gas consisting of just three molecules,

which we label a, b, and c. Let’s assume this gas has a total energy of

4e. We can achieve this by putting two molecules in the lowest, e,

energy bucket, and one in the 2e bucket. How many permutations are

possible? There are just three. We can put molecules a and b into the

lowest energy bucket and c in the next, a permutation we can label as

[ab,c]. We can also put molecules a and c in the lowest energy bucket,

and b in the next, labelled [ac,b]. The third possible permutation is

[bc,a].

Boltzmann reasoned that the most probable state of the gas would be

the one with the highest number of possible permutations for the avail-

able energy, representing maximum entropy at that energy. By equating

the maximum number of possible permutations with the most probable

distribution of energy it was a relatively simple step to the calculation of

the entropy itself.

Planck had been ﬁ ghting a losing battle against Boltzmann’s logic for

at least three years. He now succumbed to the inevitable. As he later

explained: ‘I busied myself, from then on, that is, from the day of its

establishment, with the task of elucidating a true physical character for

the [new distribution law], and this problem led me automatically to a

consideration of the connection between entropy and probability, that

is, Boltzmann’s trend of ideas.’

Even though the problem of cavity radiation appeared to be totally

unrelated to the question of whether or not a gas was composed of

atoms or molecules, Planck now reached for the statistical methods of

the atomists. But there was a catch. Because he was working backwards

from the result he was aiming for, the statistical methods he needed were

actually far removed from those used by Boltzmann.

Planck’s statistical distribution was of a subtly different kind. Boltz-

mann had examined the permutations arising from the distribution of

distinguishable molecules over the various possible energy buckets. Planck,

however, examined instead the permutations of indistinguishable energy

elements (which we continue to label as e) over the various oscillators

the most strenuous work of my life

in the cavity material. For example, if we use Planck’s methodology to

distribute four energy elements (4e) over three oscillators, then we ﬁ nd

there are now ﬁ fteen possible permutations. We can put all the elements

in the ﬁ rst oscillator, and none in the other two, a permutation which

we can write as (4e,0,0). Other permutations are (3e,e,0), (2e,e,e), (e,2e,e),

and so on.

Moreover, to get the result he wanted Planck found that the energy

elements had to be directly related to the frequency of the oscillators

(and hence the frequency of the radiation) according to his now famous

relation: e = hn—energy element equals Planck’s constant multiplied by

frequency. He further discovered that the energy elements had to be ﬁ xed

in size as integer multiples of hn. In making these choices he was follow-

ing a very different path from Boltzmann.

Many years later Planck described his state of mind as follows:

Brieﬂ y summarised, what I did can be described as simply an act of despera-

tion. By nature I am peacefully inclined and reject all doubtful adventures.

But by then I had been wrestling unsuccessfully for six years (since 1894)

with the problem of equilibrium between radiation and matter and I knew

that this problem was of fundamental importance to physics . . . A theoretical

interpretation therefore had to be found at any cost, no matter how high.

Planck, by now a willing and enthusiastic convert to the atomist view,

presented this new derivation of his radiation law to a regular fortnightly

meeting of the German Physical Society on 14 December 1900 shortly after

5 pm. As he explained to the assembled audience: ‘We therefore regard—

and this is the most essential point of the entire calculation—energy to be

composed of a very deﬁ nite number of equal ﬁ nite packages.’ He submit-

ted a paper to the journal Annalen der Physik in January 1901. About the

physical constant that was to carry his name he had this to say:

. . . since it has the dimensions of a product of energy and time, I called it

the elementary quantum of action or element of action in contrast with

the energy element hn.

The 14 December 1900 is widely acknowledged to be date on which the

quantum revolution began. But, in truth, Planck did not yet recognize

the quantum story

that his equation e = hn represented a fundamental unraveling of the

structure of classical physics.

In a possibly apocryphal tale, during a walk in the Grünewald, Planck

is reported to have told his seven-year-old son Erwin that he: ‘felt that he

had possibly made a discovery of the ﬁ rst rank, comparable perhaps only

to the discoveries of Newton.’ If true, it is likely that Planck was referring

to the discovery of the properties of the second constant in his radiation

law—which he had called Boltzmann’s constant, k—and not the discov-

ery of the quantum of action and the ﬁ xed energy elements of electro-

magnetic radiation.

Planck had used a statistical procedure, distributing the ﬁ xed energy

elements over the oscillators, without giving much thought to the

physical signiﬁ cance of this step. If atoms and molecules were real enti-

ties, something Planck was now ready to accept, then in his own mind

energy itself remained determinedly continuous, to ﬂ ow uninterrupted

back and forth between radiation and matter. But in deriving his radia-

tion law, Planck had inadvertently introduced the idea that energy itself

could be ‘quantized’. There the idea sat, in Planck’s lectures and writings,

unarticulated, unnoticed, and unremarked.

It would take true genius to see what everyone else could not.

Planck used his radiation law to score some notable successes. In 1901 he used the available

experimental data to obtain estimates for both the Planck and Boltzmann constants. He

went on to use his estimate for Boltzmann’s constant to calculate Avogadro’s number (the

number of atoms or molecules present in a characteristic amount of pure substance called

a mole).

He then used his estimate for Avogadro’s number to determine the charge of the

electron. His estimates were all accurate to within one to three per cent of the currently

accepted values for these fundamental constants.

The convert became an ardent atomist: Planck began referring to atoms and molecules

as though they were real.

But whilst Planck’s results appeared to be well-founded, there remained doubts about

his derivation; about the somewhat devious manner in which he had arrived at his result.

Many were puzzled. With the beneﬁ t of hindsight, this should not be surprising. Planck

had sprung a profoundly non-classical concept from within an otherwise entirely classi-

cal formulation. This was not something that could be done without some violence to the

classical prescription.

One young physicist who remained sceptical about Planck’s derivation was in 1905

working in the Swiss Patent Ofﬁ ce in Bern, as a ‘technical expert, third class’. His name

was Albert Einstein.

Annus Mirabilis

Bern, March 1905

A mole is the atomic or molecular weight of the substance in grams.

the quantum story

Einstein had joined the Swiss Patent Ofﬁ ce on 16 June 1902. This had been

something of a relief. After completing his graduate studies in physics at

the Zurich Polytechnic in August 1900 he had tried, and failed, to ﬁ nd an

academic position at universities in Germany, Holland, and Switzerland.

He had been unemployed for a time before ﬁ nding temporary work as a

high-school teacher.

Growing increasingly desperate about his employment prospects, he

had sought help from his fellow student and good friend Marcel Gross-

mann. Grossmann had become aware of an impending vacancy at the

Patent Ofﬁ ce and his father, who knew the director personally, was happy

to suggest Einstein’s name. Einstein had moved to Bern in anticipation of

his appointment to the post and, as he waited on a decision from the

Swiss Council, he had supported himself by offering private tuition in

mathematics and physics.

Later that year Einstein’s father, Hermann, died. On his deathbed

Hermann ﬁ nally yielded to his son’s requests and gave permission for

him to marry his student sweetheart, Mileva Maric´. Einstein had ﬁ rst

met Mileva when they both enrolled as students at the Polytechnic in

1896. She had become his muse; in their tender love letters he called her

‘Dollie’, she called him her ‘Johnnie’. However, it was not initially a match

that had met with approval from Einstein’s parents.

They were married in Bern on 6 January 1903, in a civil ceremony

witnessed by Einstein’s friends Maurice Solovine and Conrad Habicht.

Both had responded to the advert Einstein had placed in a newspaper

on his arrival in Bern, offering tutorials (with trial lessons offered free).

The three had formed a close friendship. They had held frequent discus-

sion meetings on a wide variety of subjects, proclaiming themselves the

‘Olympia Academy’.

Theirs was to be a long and enduring friendship. But there was one

secret that Einstein did not choose to share with even his closest friends.

He had fathered a child with Mileva. Their daughter, Lieserl, was born a

few days after Einstein had ﬁ rst arrived in Bern. Mileva had returned to

her parents’ home in the Serbian city of Novi Sad for the latter stages of

her pregnancy and the birth. Einstein had written of his plans to bring

Mileva and the baby to Bern once things were settled, but then their plans

changed.

annus mirabilis

Whilst Einstein’s job at the Patent Ofﬁ ce gave him the ﬁ nancial means

to support Mileva and their child, his position in Swiss ofﬁ cialdom

demanded a respectability incompatible with a child born out of wed-

lock. Mileva returned to Zurich alone, leaving Lieserl with relatives and

friends eventually, it seems, to be given up for adoption. Einstein never

saw his ﬁ rst child, or held her in his arms. All mention of Lieserl ceased;

her very existence became a close family secret.

Her ultimate fate is

unknown.

Mileva bore Einstein a second, ‘replacement’ child, Hans Albert, on

14 May 1904. By this time Einstein was settled into his job at the Patent

Ofﬁ ce. He found the work interesting, and used it to sharpen his criti-

cal intellect and ground his thinking about physical theories in terms

of their direct practical consequences. His discussions with his friends

in the Olympia Academy provided a rich diet of empiricist philosophy

and the determinism of Dutch philosopher Baruch Spinoza’s impersonal

Deus sive Natura, God or Nature. These early intellectual inﬂ uences were

to remain very powerful for the rest of Einstein’s life.

If Einstein had succeeded in his attempts to ﬁ nd an academic position,

it is quite possible that the challenge of climbing the academic career

ladder would have demanded a certain conformity, a tendency to choose

‘safe’ research topics and churn out admirable, but hardly revolutionary,

research papers. But working quietly outside the strictures of academe

left Einstein free to be rebellious, to think—even suggest—the unthink-

able.

Habicht had moved away from Bern in the spring of 1905. Einstein

wrote to him in late May to tell him of his recent work:

I promise you four papers in return. The ﬁ rst deals with radiation and the

energy properties of light and is very revolutionary . . . The second paper is

a determination of the true sizes of atoms . . . The third proves that bodies

on the order of magnitude 1/1000 mm, suspended in liquids, must already

This secret was revealed only in 1986 when researchers discovered a few, scant references to

her in Einstein’s private correspondence.

It has been suggested that Lieserl may have died from scarlet fever in September 1903.

Another hypothesis suggests that Lieserl was adopted by Mileva’s friend Helene Savic´. See

Isaacson, p. 87.